基于多目标遗传算法的机场巴士发车时刻表优化

2022-09-01巫远昆马昌喜

兰州交通大学学报 2022年4期

巫远昆，马昌喜

（兰州交通大学交通运输学院，兰州 730070）

航空运输是全球经济快速增长的贡献者之一，加速了经济全球化［1］.同时，航空运输也是我国交通运输的重要组成部分，在中长途运输，尤其是客运中发挥着重要作用.但是，由于航空运输的特殊性，机场一般都建在远离城市中心的郊区，因此机场与城市中心区域的距离一般比较长.机场巴士具有运营成本低、线路灵活、乘客乘车方便等优点［2］，是一种具有良好通达性、调度方便的公共交通工具，承担着重要的机场接驳任务［3］，可以很好的连接城市中心和机场.合理的机场巴士时刻表可以减少乘客的等车时间，降低运营成本，更好地为乘客服务.然而，许多机场巴士发车时刻表设计不合理，从而造成乘客等待时间长、时间延误大、运行效率低等问题，严重影响乘客乘坐机场巴士的积极性，甚至降低机场的运营效率.

目前，有关机场巴士时刻表设计的研究较少，学者们主要关注城市公交和轨道交通，大多数文献集中在研究城市公交和轨道交通的时刻表设计上.孙杨等［4］将乘客的到达时间设为不确定值，建立鲁棒优化模型，对公交时刻表进行优化，将结果与固定需求下的时刻表进行比较后，发现鲁棒优化后的发车时刻表抗干扰能力强，更符合需求.孙芙灵［5］从乘客需求角度出发，确定发车间隔，并建立调度模型，使用时间步长法、等效法进行求解.Li等［6］将火车线路中各站点的上下车乘客数量设为模糊值，以此建立火车发车时刻表优化模型，得到了既符合乘客需求，又降低了运营成本的发车时刻表.马天山等［7］根据乘客换乘时间分布规律建立乘客换乘总时间模型，并运用遗传算法求解，验证了模型的有效性.Sun等［8］考虑地铁运行期间高峰期和非高峰期客流的差异，以提高乘客的满意度为目标，设计不同的发车时刻表针对客流的不均匀性，减少拥堵.Salicru等［9］在等待时间比较理想的情况下，考虑了乘客的最小出行时间，设计了一种在路网中求得最优公交发车时刻表的优化算法，得到了最优公交调度方案.吴亮等［10］建立出行者与公交运营者间的双方非对称演化博弈模型，利用差异化的发车频率平衡出行者与公交运营者的利益.黄志鹏等［11］结合出行时段、列车等级和舒适性是影响旅客满意度的三个主要因素，构建旅客出行满意度双层规划模型，设计了基于模型特点的启发式算法求解，通过算例进行了仿真实验和分析，验证了该模型及算法的有效性.

然而，与城市公交发车时刻表研究所取得的巨大进展相比，机场巴士发车时刻表的优化却没有得到足够的关注，对于机场巴士的研究主要集中在客流分配和路线优化上.美国联邦航空管理局［12］提出了基于市场的六步策略，提高了美国机场的服务的质量.陆婧等［13］考虑市场培育期与机场市场份额，构建了动态巴士时刻表优化模型，并用第二代非支配排序遗传算法（non-dominated sorting genetic algorithms-II，NSGA-II）算法求解模型，动态优化了机场巴士发车时刻表.Nesset等［14］研究了多机场区域转换成本对乘客态度和忠诚度的影响.周和平等［15］构建了机场巴士线路网络的优化模型，求解旅客出行时间的最小值.包丹文等［16］为了优化了机场巴士网络，以提高可靠性的为目标，基于BP神经网络，构建了机场巴士的可靠性预测模型并求解.史澈等［17］针对现阶段国内旅客空铁联运广泛采用的机场巴士换乘模式，建立基于不同时段客流量的换乘巴士发车间隔优化模型并求解，优化机场换乘巴士发车间隔.卢天伟等［18］提出考虑弹性需求的机场客运枢纽间多方式时刻表协同优化方法，以乘客等待总时间，时刻调整总数量，时刻调整总时间最小为优化目标，构建枢纽间多方式时刻表协同优化模型，设计非支配排序遗传算法求解，缩短乘客等待时间.

在前人研究的基础上，本文考虑机场巴士时刻表设计的具体特点，对单条机场巴士线路进行研究.分析客流分布特点，考虑乘客乘车时间、等待时间和上下车取放行李时间，确定乘客出行成本优化目标，同时考虑公交公司的利益，控制运营成本，建立机场巴士发车时刻表双目标优化模型.应用NSGA-II算法，求解模型，得到多个发车调度方案，可供决策者选择.

1 模型建立

1.1 问题描述

公交发车间隔指的是某条公交线路上，上行或下行方向上的相邻两辆公交车经过同一站点的时间间隔.发车间隔长意味着发车频率低，发车次数少.减少发车次数可以降低公交公司的运营成本，但是，这会增加乘客在车站的候车时间，所以从乘客的角度考虑，应该提高发车频率减少乘客出行时间［19］.在制定发车时刻表时，不仅要考虑为乘客提供高的服务质量，还要考虑企业的成本.如果为了追求利益而降低服务质量，则违背了公交服务于乘客的原则.如果忽视了经济效益，则调度方案可能会因为运营成本过高而增加了公交公司的成本，导致调度方案中的发车时刻表无法实施.

1.2 假设条件

为了简化模型，同时减小运用多目标遗传算法对模型求解的难度，对该模型进行一些理想化的假设，具体假设如下：

1）司机服从调度安排，驾驶公交车在公交专用道上匀速行驶.

2）所有车辆都是相同的车型，且载客量足够，不会出现车站内乘客滞留现象.

3）所有车辆在规定时间进站出站，且在行驶过程中不会出现串车现象.

4）车辆沿线道路均畅通，行驶过程中无交通事故等意外事故发生.

5）车辆只在车站停靠，中途不停车.

1.3 参数符号说明

模型中出现的参数符号、参数的含义和参数的单位如表1所列.

表1 符号定义Tab.1 Summary of the notation

1.4 模型构建

以乘客出行的总时间最少和运营成本最低为优化目标构建机场巴士发车时刻表优化模型.

机场巴士每天的运营时间段内，所有乘客在车站的等车时间之和见式（1）～（2）

第二个优化目标公交公司运营费用最低目标函数见式（9）.

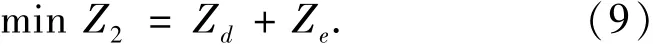
模型需满足以下约束条件：

巴士的发车间隔约束.巴士的发车间隔必须在一定的时间范围之内，如果发车间隔过长，则会导致乘客的等车时间过长，使乘客产生焦躁情绪，违背了公共交通要具有社会效益的原则；如果发车间隔过短则会导致增加公交调度的难度，使公交调度的成本过高.巴士发车间隔需满足式（10）.

2 算法求解

车辆调度属于NP-hard问题，复杂度较大，难以使用精确算法求得最优解，适合使用智能算法求解［20］.模型中的两个优化目标相互制约，一个目标的改善有可能会引起另一个目标性能的降低，故不可能同时优化两个目标，且决策者对企业效益与乘客效益的重视程度不同，难以使用固定权重的线性加权法求解.NSGA-II是基于遗传算法的多目标优化算法［21］，于2000年由Deb等［22］提出，被广泛运用于复杂的，非线性的多目标优化问题，具有解分布均匀，多样性好，有精英策略等优点，可以找到多目标优化问题的Pareto解集，求得Pareto最优解，相较于NSGA算法，NSGA-II算法使用快速非支配排序，算法的运行速度更快，复杂度更低［23］.

多目标优化问题需要寻找Pareto解集，即找到Pareto最优解，Pareto最优可以理解为，Pareto解集中的每个解相较于其他解都处于非支配地位，不存在比其中至少一个目标好且其它目标非劣的更好的解.本文采用NSGA-II求解发车时刻表优化模型.

2.1 求解步骤

算法的基本流程如图1所示.

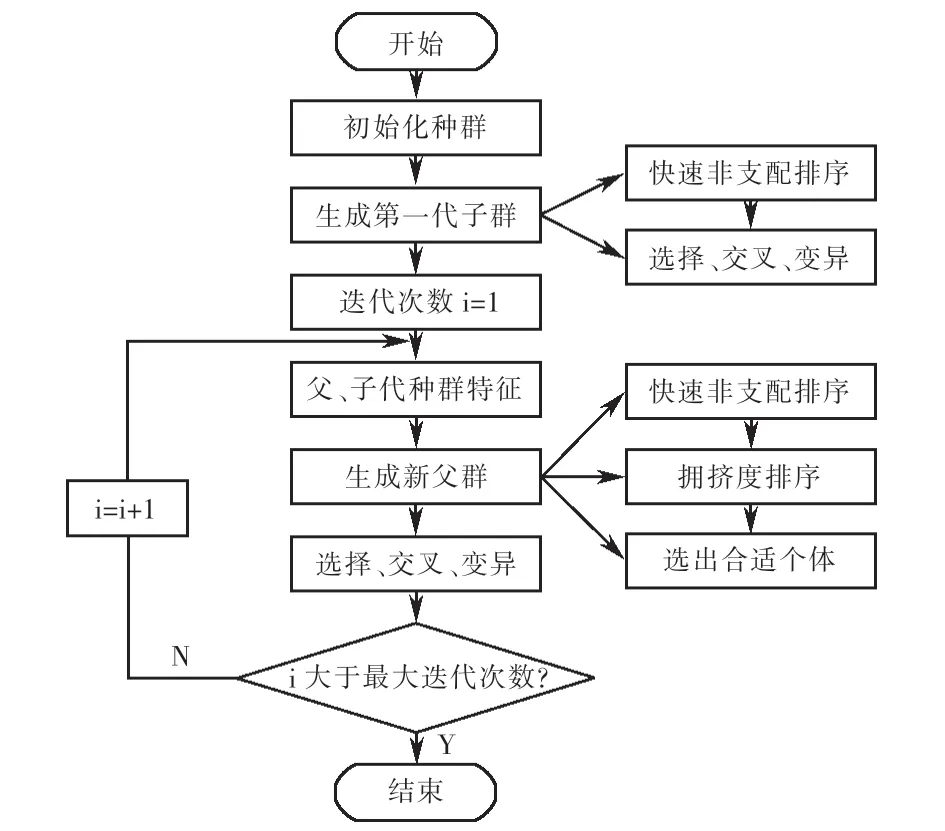
图1 算法流程Fig.1 Flow framework of solution algorithm

详细求解步骤如下：

Step1 使用随机数生成第一代父代种群P0，规模为N.

Step2 对进行快速非支配排序，快速非支配排序的过程如下：1）设定两个参数n（i）和S（i），n（i）为种群中支配个体i的个体数，S（i）为被个体i支配的个体集合.2）把种群中所有满足n（i）=0条件的个体存放在集合F（1）中，令F（1）中的所有个体i（rank）=1.3）遍历F（1）中所有被个体j支配的个体集合S（j），将S（j）中每个个体k的n（k）减1，如果n（k）-1=0，则将个体k存入集合F（2），F（2）中的所有个体i（rank）=2.4）以此类推，对集合F（2）执行操作3），直至所有个体的i（rank）都已经确定.

2.2 编码与解码策略

机场巴士调度问题的解为研究时段巴士在枢纽站的发车时刻表.我们可以先确定首班巴士在枢纽站的发车时刻，再求出研究时段内所有巴士的发车间隔，进而得到机场巴士的发车时刻表.

调度问题可以采用二进制编码或整数编码，本文采用二进制编码方法对染色体进行编码，染色体字符串长度表示整个研究时段的长度.每一位上的数字用dk表示，dk=｛0，1｝，当dk=0时，表示在该时刻不发车；当dk=1时，表示在该时刻发车.以下举例时间精度为10 min，则染色体编码示意图如图2所示.

图2 染色体编码示意图Fig.2 Chromosome coding diagram

解码后可以得到，研究时段长度为340 min，在这个时间段内共发车9次，假设首班车发车时间为10∶00，那么这9班车分别在10∶00、10∶30、11∶30、12∶20、13∶10、13∶40、14∶10、14∶50、15∶40发车.

3 实例分析

以兰州市中川国际机场某条机场巴士线路为研究对象，优化该线路的巴士发车时刻表.该线路全长71 245 m，最大发车次数限制13次，客流在时间分布上具有一定的不均匀性.该线路共6个站点，巴士在城市路段（站点1-5）平均车速为20 km/h，在高速路路段（站点5-6）平均车速为90 km/h.选取6∶00～14∶00时间段验证发车时刻表优化模型.

3.1 参数标定

模型的相关参数，各站点间的距离和巴士在相邻两站间的行驶时间如表2～4所列.

表2 模型参数标定Tab.2 Model parameter calibration

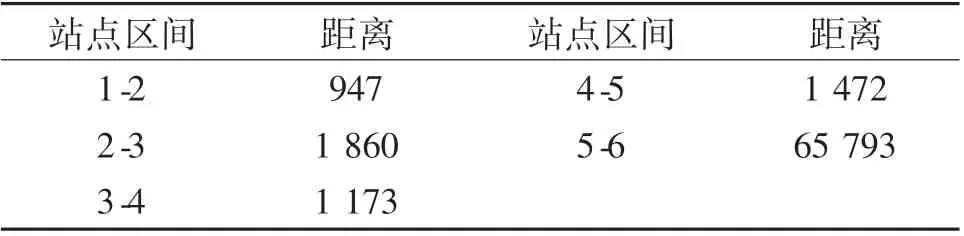
表3 各站点间距Tab.3 Distance between stations m

3.2 仿真结果分析

使用NSGA-II算法对模型进行求解，设置初始种群规模为50，迭代次数为500，选择操作采用二进制锦标赛法，交叉操作采用单点交叉，变异操作采用二进制变异，交叉概率和变异概率分别设置为0.9和0.3.使用C++仿真后共得到11个结果，将所有结果在平面坐标中标定出来，绘制出行成本与运营成本关系图，如图3所示.

图3 出行成本与运营成本的关系Fig.3 Relationship between travel cost and operation cost

从出行成本与运营成本关系图中可以看出，形成了较为明显的pareto前沿面，其中，符合约束条件，能较好平衡乘客和公交公司利益的解有5个，调度方案如表5所列.

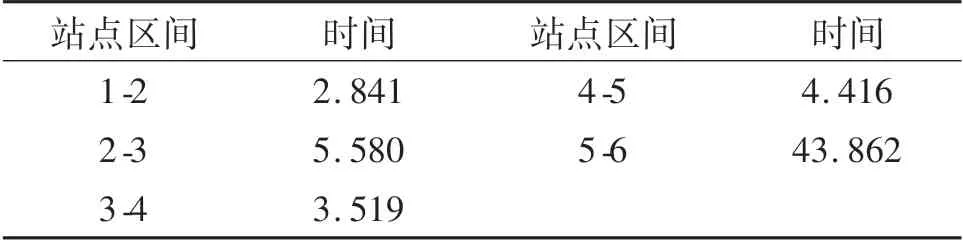
表4 车辆在相邻站点间的行驶时间Tab.4 Driving time between stations min

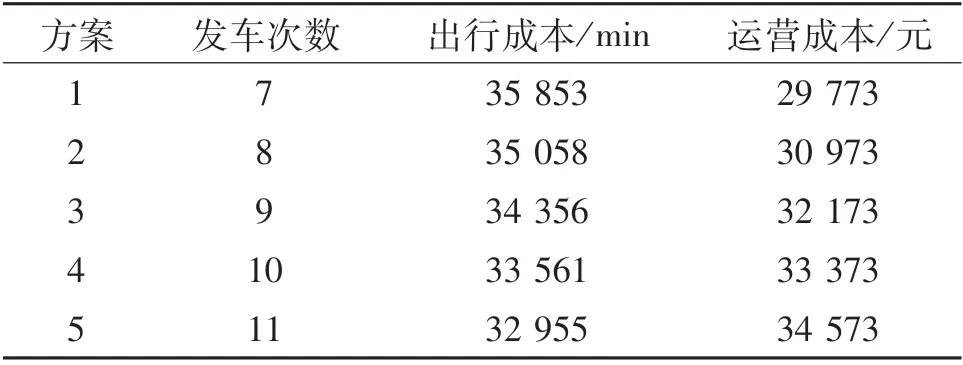
表5 调度方案Tab.5 Dispatching scheme

以上方案中，当决策者主要注重企业利益时，可选择方案1；当决策者主要注重机场巴士的社会效益时，可选择方案5.在发车次数相同的前提下，将传统的固定发车间隔的发车调度方案与5种优化后的备选方案作对比，得到的结果如图4所示.

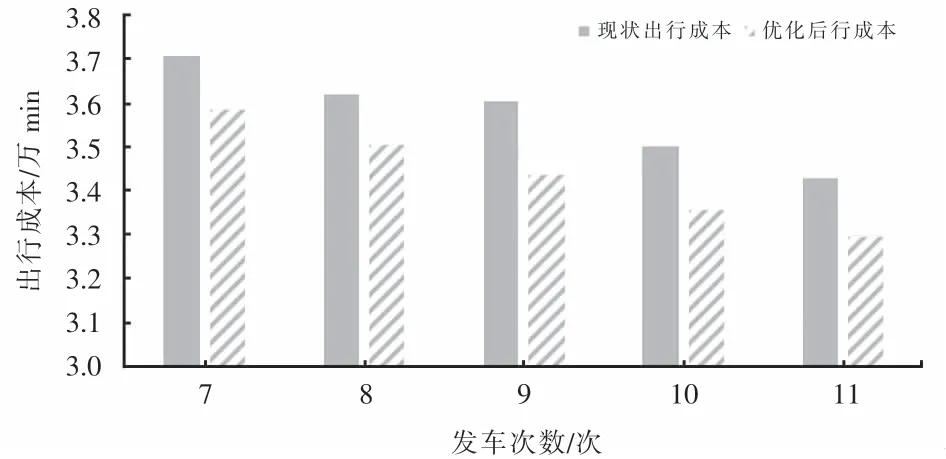
图4 优化前后出行成本比较Fig.4 Comparison of travel costs before and after optimization

从图中可以得出，在发车次数相同的情况下，优化后发车方案的出行成本皆低于原发车方案，较原发车方案出行成本平均下降3.84%，发车9次时出行成本下降最显著，出行成本降低了4.62%.综合权衡乘客时间成本和企业运营成本，选择方案3为相对最优调度策略，得到的发车时刻如表6所列.考虑了客流随时间分布的不均匀性，在早高峰期提高了发车频率，减小了乘客的等车时间，同时仅比传统的整点发车调度方案增加一次发车，也兼顾了公交公司的利益.

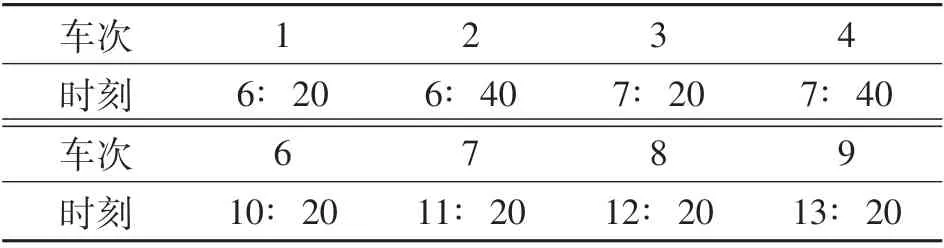
表6 最优发车时刻表Tab.6 Optimized timetable

3.3 行驶速度灵敏度分析

对巴士的行驶速度进行灵敏度分析，把巴士的速度提高5、10、15、20 km/h，计算发车次数为9时，解的出行成本如图5所示.

图5 巴士速度与出行成本的关系Fig.5 Relationship between bus speed and travel cost

由图5可以看出，随着巴士速度的提升，出行成本从34 356减少至26 747，但是速度每提升5 km/h，出行成本减少的值逐渐变小.实际中，决策者可以提高巴士速度来降低乘客出行成本，但是速度提高值过高时，降低乘客出行成本的效率会降低，且在城市中如果巴士的速度太快，会影响乘客的乘车舒适度以及增加行车的危险性.