波汶钢腹板-钢底板组合箱梁的挠度分析
2022-09-01毛亚娜刘世忠李爱军秦翱翺贡保甲
毛亚娜,刘世忠,郭 华,李爱军,秦翱翺,贡保甲
(1.兰州交通大学 土木工程学院,兰州 730070;2.甘肃省公路航空旅游投资集团有限公司,兰州 730030;3.中铁上海设计院集团有限公司,上海 200070)
波纹钢腹板-钢底板-混凝土顶板(corrugated steel web-steel bottom,CSWSB)组合箱梁与常规混凝土底板波纹钢腹板(corrugated steel web-steel,CSW)组合箱梁相比具有阶段拼装工序少、自重更轻、底板抗拉(抗裂)性能强等特点,特别是能减少运营期维护工作量、避免混凝土底板产生裂缝的病害.
国外对波纹钢腹板组合箱梁的研究远早于国内,Elgaaly等[1]认为波纹钢腹板几乎没有对主梁抗弯的贡献,其抗弯刚度可以忽略,CSW 箱梁的抗弯能力由混凝土顶板和底板提供;Sayed-Ahmed[2]认为CSW 组合梁剪力和弯矩互不耦合,且波纹钢腹板自身抗弯作用可以忽略;Chan等[3]对多种类型的钢板箱梁进行了研究;Oh等[4]提出的将平面的钢腹板转变成褶皱形的钢腹板,能有效提高CSW 组合梁的预应力效应.
国内学者对CSW 组合箱梁的研究相对较晚.自上世纪90年代起,鉴于部分发达国家所建造的多座CSW 组合箱梁桥投入运营且效果良好,国内学者对CSW 组合箱梁的研究相对较晚.自上世纪90年代起,鉴于部分发达国家所建造的多座CSW 组合箱梁桥投入运营且效果良好,国内设计工程师和科研院所的学者们对该CSW 桥梁开展了大量的理论和试验研究,为我国CSW 桥梁的设计和建造提供了基础性理论技术支撑.文献[5-7]通过研究得到了CSW箱梁顶、底板的应力分布和变形规律,揭示了裂缝产生的原因;徐岳等[8]通过研究发现波纹钢腹板的抗弯作用在桥梁验算中的贡献甚微,基于截面弯曲理论,建立了CSW 箱梁的抗弯承载力计算公式;文献[9-10]通过自编程序研究了CSW 箱梁受弯过程中的非线性表现;冀伟等[11]给出了波纹钢腹板-钢底板-混凝土顶板组合简支箱梁竖向振动频率的计算公式,并进行了参数分析.本文在国外内学者的研究基础上,对CSWSB箱梁的变形理论进行探讨分析.
1 CSWSB箱梁的变形理论分析
在分析CSW 组合箱梁普遍采用的“拟平截面假定”的基础上,对由混凝土顶板和钢翼缘板界面的滑移和钢腹板剪切变形引起的附加挠度进行剥离分析,探究两种附加挠度对CSW 箱梁总挠度的影响.采用折线模型来描述剪切应力与滑移之间的关系[12],如图1所示.Δμ为界面相对滑移,σ为界面间法向正应力,τ为界面剪应力,τ1为切向粘聚强度峰值.
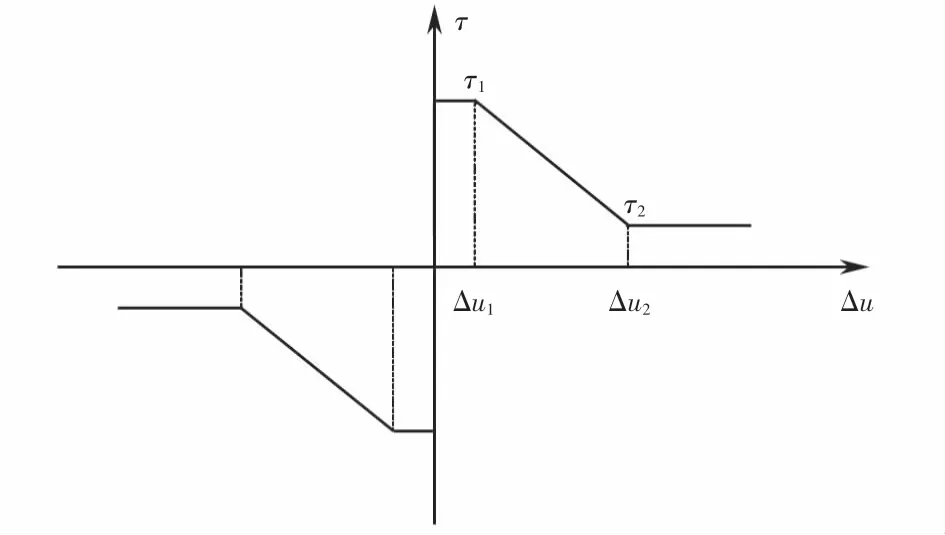
图1 界面剪切应力与滑移关系示意图Fig.1 Schematic diagram of the relationship between interfacial shear stress and slip

1.1 CSWSB箱梁界面滑移引起的附加挠度
CSWSB箱梁在外荷载作用下,混凝土顶板和波纹钢腹板上部与其接触的钢翼缘板(下文简称钢翼板)存在界面滑移现象.这一现象使得箱梁的抗弯刚度降低,从而使箱梁挠度增大(产生附加挠度),同时形成附加弯矩.
基本假定:
1)界面发生剪切滑移前,混凝土顶板和钢底板应变关系满足拟平截面假定;
2)钢翼板和混凝土顶板界面剪切滑移值与水平剪力呈线性关系;
3)波纹钢腹板处于弹性工作状态;
4)波纹钢腹板对主梁纵向的抗弯贡献为零,波纹钢腹板仅承受竖向剪力;
5)钢翼缘板与混凝土顶板始终密贴.
根据脱离体平衡和变形协调关系,如图2所示.列出CSWSB箱梁界面滑移微分方程,再依据简支边界约束条件与荷载作用模式,推导由界面滑移引起的附加挠度计算公式.s1为钢翼缘板和混凝土顶板之间的界面滑移;r为脱离体在单位长度上的相互挤压力;FN,M,Q分别为轴力、弯矩和剪力.

图2 CSWSB箱梁各部分受力图示Fig.2 Stress diagram of each part of CSWSB box girder


边界条件:当在纵向梁长x=0时,S=0;当x=l/2时,S′=0,剪力则为Q=P/2,波纹钢腹板-钢底


简支箱梁两个对称集中力P作用下,受力图示如图4所示.根据弯矩和剪力的分布划分为纯弯区和弯剪区,为纯弯区的长度.
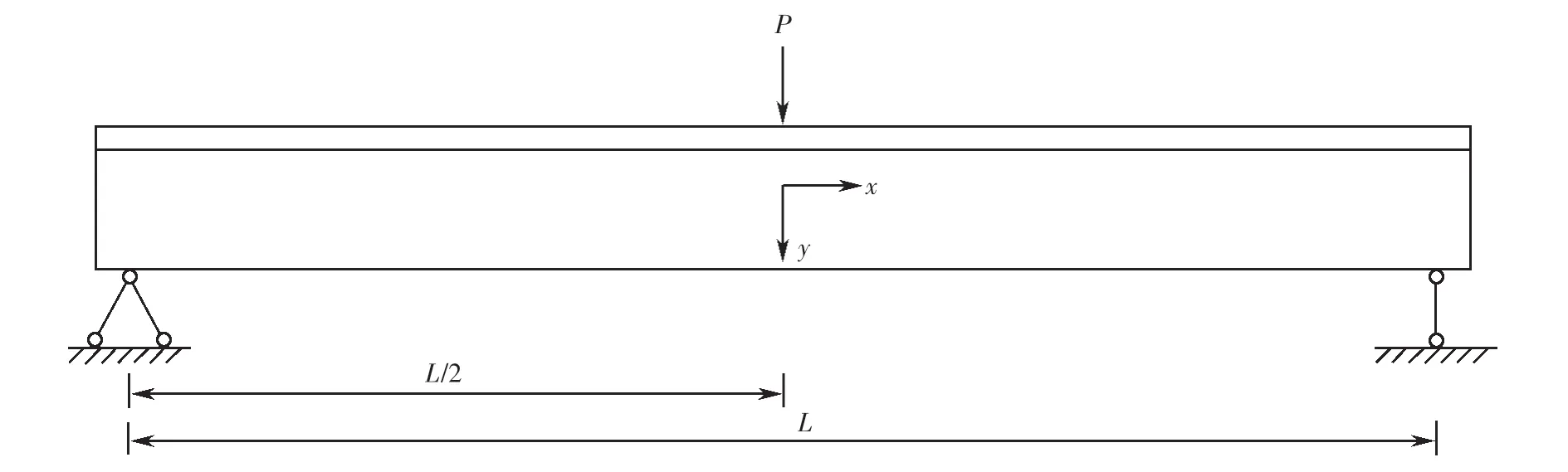
图3 跨中集中荷载作用Fig.3 Mid-span concentrated load
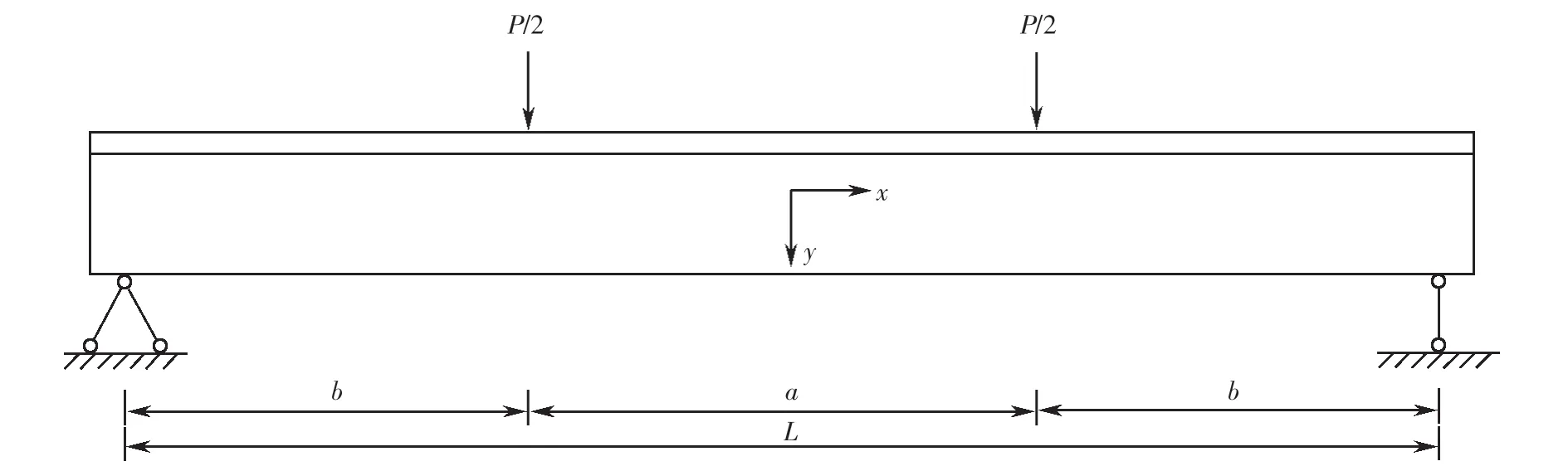
图4 跨中纯弯加载PFig.4 Pure bending load P in mid-span




设计制作的比例模型如图5所示.b为混凝土顶板宽度,h1为钢翼缘板厚度,h2为腹板厚度,b1为钢翼缘板宽度,b2为钢底板宽度,h0为换算截面的中性轴和混凝土桥面板上的翼缘的距离,hF为腹板高,hs为钢箱梁中心轴到混凝土顶板上部距离,hc为顶板厚,h为梁高.
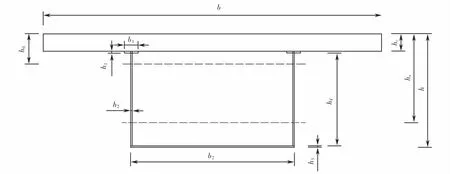
图5 模型尺寸示意图Fig.5 Schematic diagram of model size

1.2 剪切变形引起的附加挠度计算
施加静荷载时箱梁的变形计算方法主要包含两种[18]:欧拉梁理论与铁木辛柯梁理论.当箱梁高跨比较大时必须计入剪切变形附加挠度,此时依据铁木辛柯梁理论来计算其挠度.当箱梁高跨比较小时忽略剪切变形附加挠度而利用欧拉梁理论进行计算[19].考虑剪切变形时梁微段的变形图如图6所示.左图表示截面受不均匀剪应力作用,使与箱梁中性轴垂直的平面发生了翘曲变形;右图表示截面上受均布剪应力,而使原截面不垂直于中性轴,但仍然保持平面.
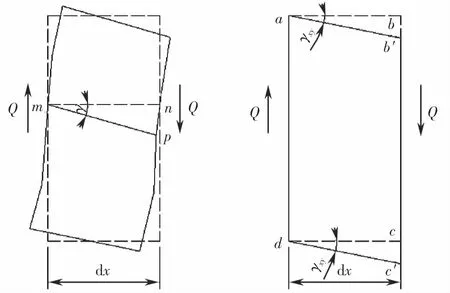
图6 剪切变形示意图Fig.6 Schematic diagram of shear deformation
则由剪切作用引起的梁挠曲线的斜率与截面剪应变的关系式可表示成[18]:

于是得到波纹钢腹板-钢底板的组合箱梁剪切变形微分方程:
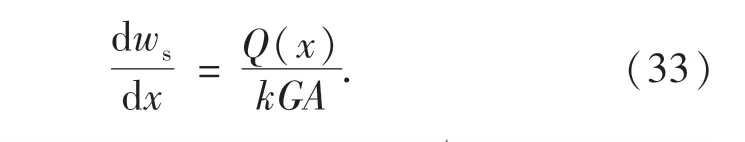

2 模型试验验证
为了验证推导的CSWSB箱梁挠度公式的正确性,基于结构相似原理,制作了1∶5跨径=8 000 mm的波纹钢腹板钢-钢底板组合箱梁试验模型梁,C50混凝土顶板,波纹钢腹板Q235钢.试验梁各部具体尺寸如图7~10所示.

图7 模型试验梁立面尺寸图(单位:mm)Fig.7 Model test beam elevation dimension(unit:mm)
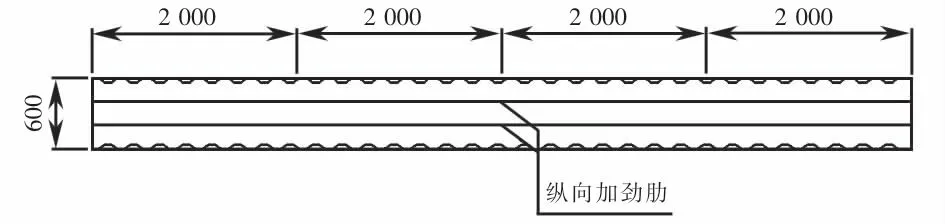
图8 模型试验梁底板剖面尺寸(单位:mm)Fig.8 Sectional dimensions of the base plate of the model test beam(unit:mm)
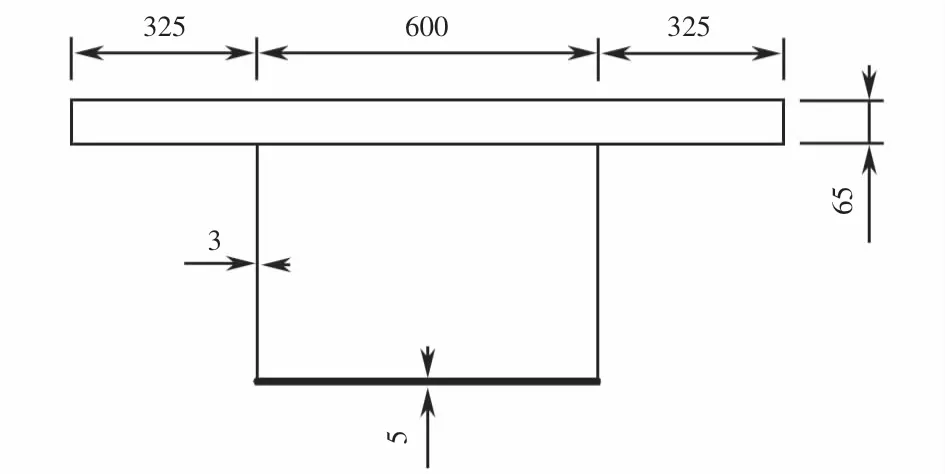
图9 模型试验梁横截面尺寸图(单位:mm)Fig.9 Dimensions of the cross-section of the beam in the model test(unit:mm)
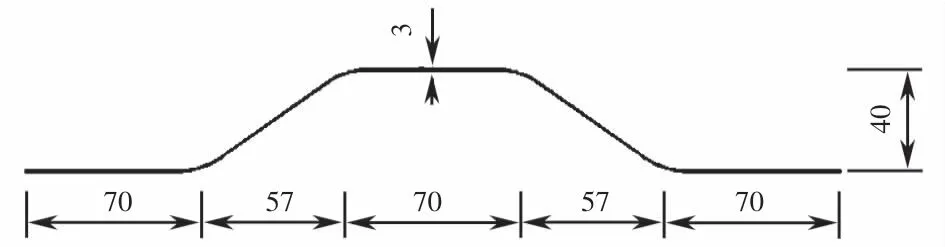
图10 波纹钢腹板波段尺寸图(单位:mm)Fig.10 Wave band dimension drawing of corrugated steel web(unit:mm)
2.1 加载方式
加载吨位由荷载传感器实测控制,由分配梁将千斤顶作用的荷载传递到混凝土块上,混凝土块置于试验梁的顶面.对试验梁进行静力加载,测试在跨中加载和跨中对称纯弯加载下,各观测截面的挠度变化、界面滑移分布、应变分布、波纹钢腹板的剪应力分布.具体加载工况:
1)跨中加载时主要在弹性阶段测试,以便接下来进行跨中对称纯弯加载,因而施加的荷载较小,以5 kN为一个级递进加载,加载至极限荷载值的70%,每级加载后持荷15 min,采集模型梁各级荷载下的各测试截面的应变、挠度和滑移值;
2)跨中对称纯弯加载时荷载增量仅增加到弹塑性阶段上限,与跨中加载时相对极限荷载值大,以10 kN为一个荷载级递增,每级加载后持荷15 min,采集相关数据.
2.2 有限元模型的建立
采用ANSYS 18.0软件建立考虑界面滑移的组合箱梁三维有限元模型,波形钢腹板采用shell单元顶板采用solid单元,边界条件按照简支梁模拟,三维有限元模型如图11所示.
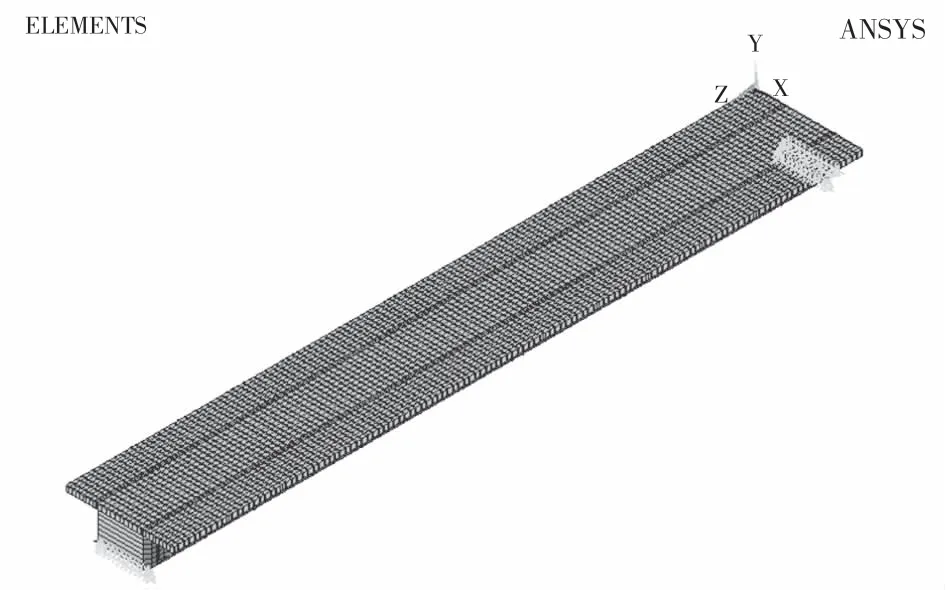
图11 考虑界面滑移的组合箱梁模型Fig.11 Composite box girder model considering interface slip
2.3 理论值、试验实测值和有限元结果对比分析
为探明波纹钢腹板-钢底板组合箱梁桥在不同静力荷载工况下的力学特性,通过模型试验加载测试、理论公式计算和三维有限元仿真等手段,对波纹钢腹板-钢底板组合箱试验模型进行多工况理论与试验分析结果对比.模型梁跨中挠度有限元数值解和理论公式结果对比如图12所示.
由图12可知试验梁加载测试结果显示,剪切变形和界面滑移对试验梁的挠度影响不可忽略.试验梁挠度与荷载梯度基本呈线性关系,与国内其他学者的研究结果一致.跨中加载试验的荷载没有超过弹性荷载上限,实测挠度与荷载的曲线呈正比.

图12 试验梁跨中各级加载挠度对比Fig.12 Comparison of loading deflections at all levels in the mid-span of the test beam
对称加载试验中,模型梁跨中挠度有限元数值解和理论公式结果对比如图13所示.
由图13可知,同一测点的实测挠度值,在前期随着荷载梯度的增加呈线性增长;在最后荷载-挠度呈非线性增长,经观察是试验梁的顶板逐渐开裂且剪力钉发生滑移所致,曲线以及进入非线性阶段.
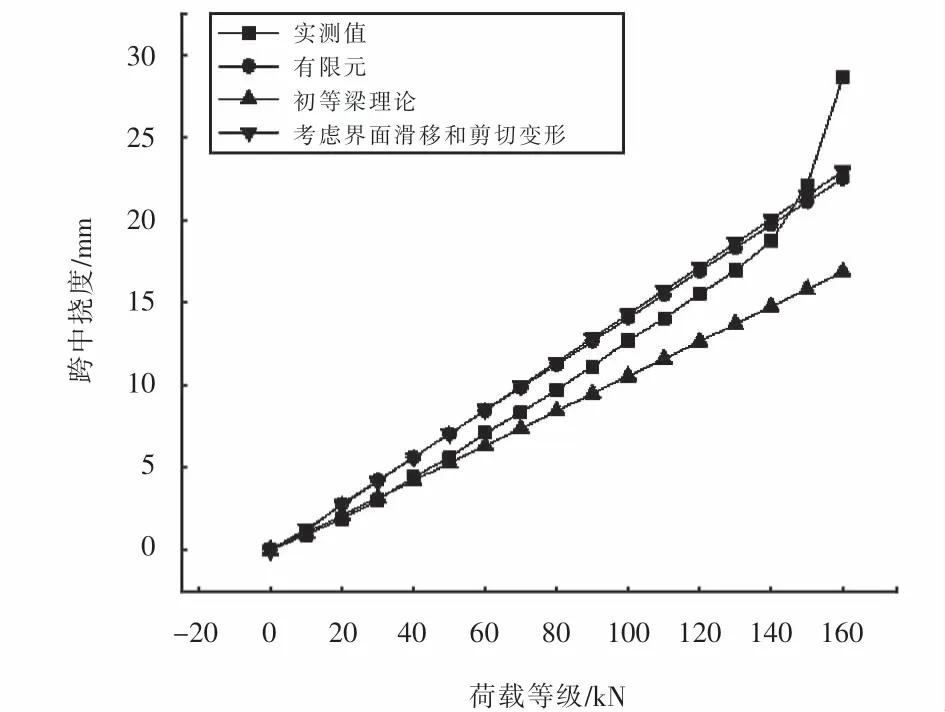
图13 试验梁对称纯弯各级加载挠度对比Fig.13 Comparison of loading deflections at all levels of symmetrical pure bending of test beams
3 高跨比对挠度的影响
为研究箱梁不同高跨比时剪切变形及界面滑移对波纹钢腹板-钢底板在相同荷载作用下跨中加载和对称纯弯加载挠度影响程度,箱梁高跨比取值范围为1/6~1/52,其他条件与试验梁保持不变,理论计算与有限元分析结果,如图14~15所示.
由图14~图15可知,波纹钢腹板-钢底板组合箱梁桥随着跨径的增大(H/L变小)时,界面滑移产生的附加挠度和剪切变形产生的附加挠度在逐渐减小;随着跨径的增大,界面滑移和剪切变形对CSWSB箱梁最大挠度的影响逐渐减小.当高跨比大于0.05时,界面滑移的影响大于20%;而剪切变形的影响大于5%.波纹钢腹板-钢底板的组合箱梁在截面尺寸不变时,高跨比大于0.05时,剪切变形和界面滑移引起的附加挠度不可忽略.
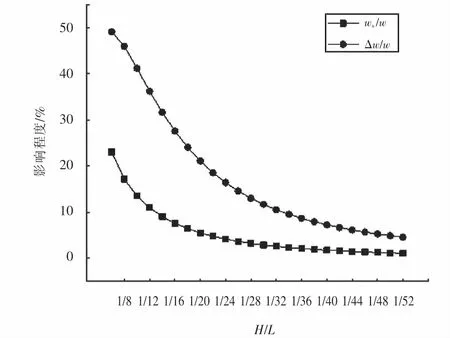
图14 跨中集中力作用下高跨比对跨中挠度的影响Fig.14 Effect of height-to-span ratio on mid-span deflection under concentrated force in mid-span

图15 两点对称加载作用下高跨比对跨中挠度的影响Fig.15 Effect of height-to-span ratio on midspan deflection under two-point symmetrical loading
4 结论
通过本文分析,得到了以下结论:
1)基于静力法和铁木辛柯梁理论,推导了CSWSB箱梁界面滑移和剪切变形引起的附加挠度微分方程,得出了两种附加挠度的计算公式.
2)在“拟平截面假定”的基础上,对由界面滑移与剪切变形引起的CSWSB箱梁附加挠度进行分离解析:分析了两种附加挠度对箱梁总挠度计算精度的影响,结果表明界面滑移影响大于剪切变形.
3)当高跨比小于0.05时,界面滑移引起的附加挠度占比最大小于20%;而剪切变形的附加挠度占比最大小于5%,因而在波纹钢腹板-钢底板的组合箱梁的截面尺寸不变时,当跨度变化使高跨比大于0.05时,剪切变形和界面滑移引起的跨中附加挠度不可忽略.
