机载雷达深度展开空时自适应处理方法

朱晗归 冯为可 冯存前 邹帛 路复宇

(空军工程大学防空反导学院 西安 710051)

1 引言

空时自适应处理(Space-Time Adaptive Processing，STAP)是机载雷达地/海杂波抑制和运动目标检测的关键技术[1，2]。为设计空时滤波器自适应抑制杂波，STAP方法一般需要利用一定数量的独立同分布(Independent Identically Distributed，IID)训练距离单元估计待测距离单元(Range cell Under Test，RUT)的杂波协方差矩阵(Clutter Covariance Matrix，CCM)。为保证输出信杂噪比相比理想条件的损失不超过3 dB，传统STAP方法所需IID训练单元的数量至少为系统自由度的2倍。然而，在实际非均匀杂波环境中，通常难以获得足够的IID训练单元。为解决这一问题，学者提出降维、降秩、直接数据域、知识辅助和稀疏恢复等STAP新方法[3—8]。其中，稀疏恢复空时自适应处理(SR-STAP)方法基于杂波在角度-多普勒域(即空时二维平面)的稀疏特性，利用少量训练距离单元即可获得杂波空时谱的准确估计，从而重构CCM或杂波子空间，构造空时滤波器对杂波进行抑制[9—16]。

在实际应用中，机载雷达不可避免地存在着阵列误差，包括幅度误差和相位误差。由于误差信息隐含于CCM的估计之中，传统STAP方法具有较强的误差自适应补偿能力。然而，由于SR-STAP方法通常利用理想空时导向矢量构建杂波空时谱估计模型，其性能受误差的影响较大。阵列误差会降低杂波空时谱及CCM的估计准确性，从而严重影响SR-STAP方法的杂波抑制和目标检测性能。针对这一问题，文献[17]提出了基于迭代交替下降(Iterative Alternating Descent，IAD)算法的SR-STAP方法，能够同时估计杂波空时谱和阵列误差参数，但该方法的运算复杂度较高；文献[18]提出了基于ADMM算法的杂波空时谱和阵列误差参数联合估计方法，相比IAD方法运算复杂度较低，但需要同时对多个迭代参数进行设置。

在构建杂波空时谱估计模型或杂波空时谱及阵列误差参数联合估计模型的前提下，现有SR-STAP方法的性能往往依赖于所采用的SR算法。目前，典型的SR算法均基于模型驱动实现，具有理论保证性高、可解释性强等优点。但是，模型驱动类SR算法通常需要设置一个或多个参数，例如正则化因子、迭代步长等。不恰当的参数设置会影响SR算法的收敛速度和精度，从而使得SR-STAP方法的运算复杂度升高、杂波抑制性能下降，限制了其在实际中的应用。针对模型驱动类SR算法存在的问题，受深度学习技术的启发，学者提出了DU方法[19—23]。DU方法将特定SR算法展开为深度神经网络，将算法的迭代次数作为网络的层数、算法的参数作为网络的学习参数，利用训练数据集对SR算法所涉及的迭代参数进行训练，获得最优参数，从而提高SR算法的收敛速度和精度。例如，Gregor等人[19]基于迭代软阈值算法(Iterative Soft Thresholding Algorithm，ISTA)，提出了学习型ISTA(Learned ISTA，LISTA)算法；Borgerding等人[21]对近似消息传递(Approximate Message Passing，AMP)算法进行展开，提出了LAMP算法；Yang等人[22]基于近端算子方法(Proximal Operator Methods，POM)，提出了LePOM算法。相比其对应的SR算法，DU方法将模型驱动和数据驱动相结合，能够有效降低算法复杂度、提高算法性能。

目前，尚未有研究将DU方法引入到机载雷达SR-STAP之中，且上述DU方法仅能用于杂波空时谱估计，无法同时估计阵列误差参数。因此，为解决现有SR-STAP方法存在的参数设置困难和运算复杂度高等问题，本文提出了机载雷达DU-STAP方法，以验证DU方法在机载雷达杂波抑制和目标检测中的适用性。首先，建立了阵列误差条件下的机载雷达回波信号模型，并利用ADMM算法对杂波空时谱和阵列误差参数进行联合估计；接着，根据对其迭代步骤和数据流图的分析，将ADMM算法展开为深度神经网络，构建具有正则化因子、迭代步长、二次惩罚因子和比例因子等可学习参数的AE-ADMM-Net；然后，定义网络损失函数，基于充足完备的数据集对AE-ADMM-Net进行训练，获得最优参数；最后，利用训练后的AE-ADMM-Net对训练距离单元数据进行处理，快速获得杂波空时谱和阵列误差参数的准确估计，从而设计空时滤波器进行杂波抑制和目标检测。仿真实验表明：相比基于稀疏贝叶斯学习(Sparse Bayesian Learning，SBL)算法[13]、欠定系统聚焦式求解算法(Focal Under-determined System Solver，FOCUSS)[10]和ADMM算法的典型SR-STAP方法，本文所提出的DU-STAP方法均能够在保持较低运算复杂度的同时提高杂波抑制性能。

2 理论基础

2.1 信号模型

如图1所示，假设机载雷达以高度H、速度v沿y轴匀速飞行，正侧视均匀线阵的阵元个数为M，阵元间距为d=λ/2(λ为波长)，脉冲重复频率为fr，在一个相干处理间隔内共有N个脉冲。

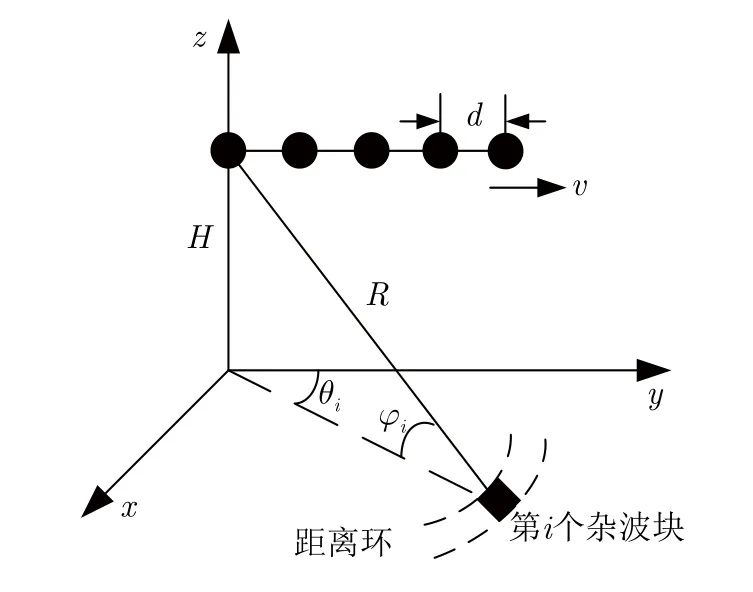
图1 机载雷达几何模型Fig.1 Geometry model of airborne radar

不考虑距离模糊杂波的影响，假设每个距离单元所对应的距离环中共有Nc个杂波块均匀分布在方位角θ∈[0，π]上，则包含运动目标的RUT空时回波信号可表示为

假设各个杂波块之间相互独立，与噪声不相关，且噪声服从均值为0、协方差矩阵为RN=σ2INM的复高斯分布，则杂波加噪声协方差矩阵(Clutter plus Noise Covariance Matrix，CNCM)可表示为

其中，E[·]表 示期望，[·]H表示共轭转置，INM表示NM ×NM的单位矩阵。

STAP通过计算空时回波信号的加权组合实现对杂波和噪声的抑制以及对运动目标的检测。为使输出信杂噪比(Signal to Clutter plus Noise Ratio，SCNR)最大，空时滤波器的最优权值可通过式(3)计算得出：

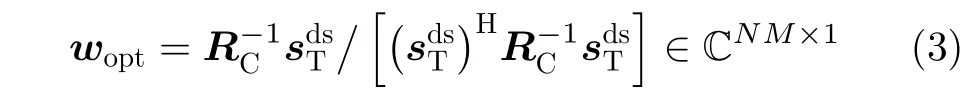
其中，(·)-1表示对矩阵求逆。

实际上，RUT的CNCM是未知的，一般需要一定数量的无目标训练距离单元对其进行估计。假设训练距离单元与RUT的杂波独立同分布，则RUT的CNCM可以通过采样协方差矩阵求逆(Sample Matrix Inversion，SMI)方法估计得到[1]，表示为

其中，l=1，2，...，L，L表示IID训练距离单元个数，yl表示第l个训练距离单元的空时回波信号。

根据RMB准则[2]，SMI方法确保输出SCNR损失小于 3 dB所需的 IID 训练距离单元数应至少为2 倍的系统自由度。在实际非均匀环境中，该条件通常难以得到满足。此外，实际机载雷达不可避免地存在阵列幅相误差。此时，RUT空时回波信号、CNCM和最优空时权值可分别表示为

2.2 SR-STAP

由式(1)可以看出，杂波信号可由不同空间频率和多普勒频率的空时信号叠加而成。如果分别将空间频率和多普勒频率离散化为Ns=κsM和Nd=κdN个网格点(其中κs＞1和κd＞1表示尺度因子)，则第l个无目标训练距离单元的空时回波信号可表示为

根据杂波空时谱的稀疏性，可将欠定问题(8)转化为如下约束优化问题进行求解：

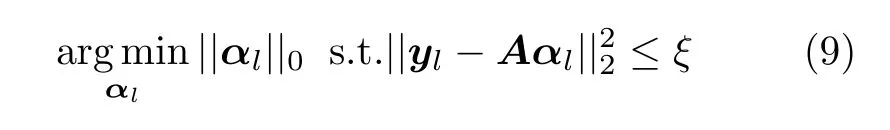
其中，||·||0和||·||2分别表示向量的L0范数和L2范数，ξ表示噪声电平。

在存在L个训练距离单元的情况下，式(9)可扩展至多观测模型，表示为

利用L1凸优化算法、FOCUSS算法或SBL算法等稀疏恢复算法对式(9)或式(10)进行求解，可获得αl或Λ的高分辨估计。然后，可通过式(11)计算CNCM，并根据式(3)设计空时滤波器：

同理，当存在阵列误差时，第l个训练距离单元的空时回波信号可表示为

其中，E=IN ⊗diag(e)，IN表示N×N的单位矩阵，d iag(·)表示取对角矩阵。

此时，需要同时估计杂波空时谱αl和阵列误差参数e，表示为

在求解(13)的基础上，CNCM可通过式(14)进行计算，从而根据式(7)设计空时滤波器：

SR-STAP方法利用少量甚至单个训练距离单元即可获得CNCM的准确估计，从而实现对杂波的抑制，在实际非均匀环境中具有显著优势。为简便起见，本文仅考虑单个训练距离单元的情况，即L=1，多个训练距离单元的情况可对本文算法进行拓展处理。此外，需要说明的是：在存在距离模糊的情况下，仍然可以建立如式(9)或式(10)所示的优化模型，利用SR算法进行求解，获得距离模糊杂波空时谱的高分辨估计，具体可参考文献[24，25]。

3 DU-STAP方法

为降低运算复杂度、提高杂波抑制性能，本文拟利用DU方法对杂波空时谱和阵列误差参数联合估计模型(13)进行求解。由文献[21]可知，对于y=Aα+ε所示的稀疏恢复问题，大多迭代类SR算法的步骤可表示为αk+1=P(αk-γkAH(Aαk-y))。其中，αk为第k次迭代估计结果，γk为迭代步长，P(·)为 非线性算子。令Wk=INM -γkAHA，Bk=γkAH，则SR算法的第k次迭代等价于αk+1=P(Wk·αk+Bky)。将Wk和Bk定义为深度神经网络的权重参数，P(·)定义为深度神经网络的激活函数，αk和αk+1分别定义为深度神经网络第k层的输入和输出，则SR算法的第k次迭代等价于深度神经网络的第k层运算。因此，DU方法可以看作基于SR算法的迭代步骤对深度神经网络的结构和参数进行设计。理论上，LISTA，LAMP和LePOM等DU方法[19—21]均可以实现对杂波空时谱的估计，即对式(9)进行求解。然而，这些方法无法同时估计阵列误差参数，即无法对式(13)进行求解。针对这一问题，本文对ADMM算法[18]进行分析，将其展开为深度神经网络，构建AE-ADMM-Net，实现对杂波空时谱和阵列误差参数的快速准确估计。

3.1 ADMM算法

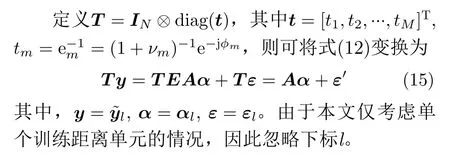
式(15)将阵列幅相误差矢量e转化为参数矢量t，可通过式(16)进行求解：

其中，ρ＞0表示正则化因子。

定义辅助变量η=T y-Aα，则式(16)可等效为

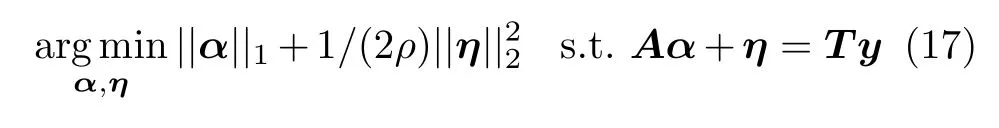
等式约束问题(17)的增广拉格朗日函数可表示为

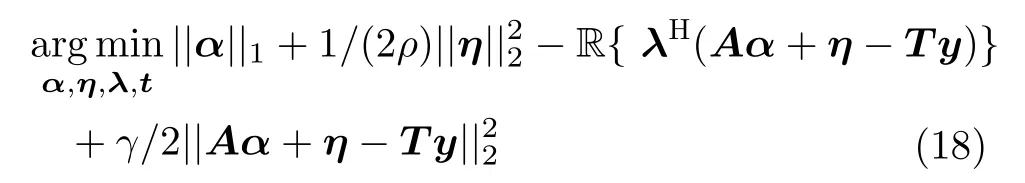
其中，δ∈R，w∈R 为比例因子，β为辅助参数，(·)*表示共轭。

ADMM算法利用K次迭代交替求解以下4个子问题对式(19)进行求解[18]：

其中，τ为α的迭代步长，soft(x，c)=max{|x|-c，0}·x/|x|为软阈值算子[19]，

综上所述，利用ADMM算法对式(13)进行求解的步骤如表1所示。需要强调的是：当不存在阵列误差时，表1所示的ADMM算法同样可以对式(9)进行求解。此时，可跳过步骤4，并令T(k+1)=T(0)保持不变；也可令比例因子δ=M，w=0，ADMM算法将输出阵列误差的估计e≈1M，即νm≈φm≈0。

ADMM属于模型驱动类算法，其正则化因子ρ、二次惩罚因子γ、迭代步长τ、比例因子δ和w等参数均需提前给定。在实际应用中，参数的设置是比较困难的。不恰当的参数设置会影响ADMM算法的收敛速度和精度，从而使式(13)的求解复杂度升高、杂波空时谱和阵列误差参数的估计准确性下降。即使能够通过理论分析、交叉验证的方法选择合适的参数，固定的参数设置并不能保证ADMM算法获得最好的收敛效果。为解决上述问题，基于DU方法的思路，本文将ADMM算法展开为深度神经网络AE-ADMM-Net，利用学习的方法获得其最优迭代参数。为构建AE-ADMM-Net，将ADMM算法的迭代步骤映射为一个数据流图，如图2所示。

图2所示数据流图主要由ADMM算法所对应的不同图节点和不同图节点之间表示数据流动的有向边组成。数据流图的第k+1层表示ADMM算法的第k+1次迭代，表1的迭代步骤2—步骤5对应4个图节点：辅助变量更新节点(X(k+1))、杂波空时谱更新节点(O(k+1))、误差参数更新节点(Z(k+1))和拉格朗日乘子更新节点(M(k+1))。可以看出：ADMM算法的K次迭代可以映射为一个K层的数据流图，输入的空时回波信号沿此数据流图进行传递，将获得杂波空时谱和阵列幅相误差的估计结果。

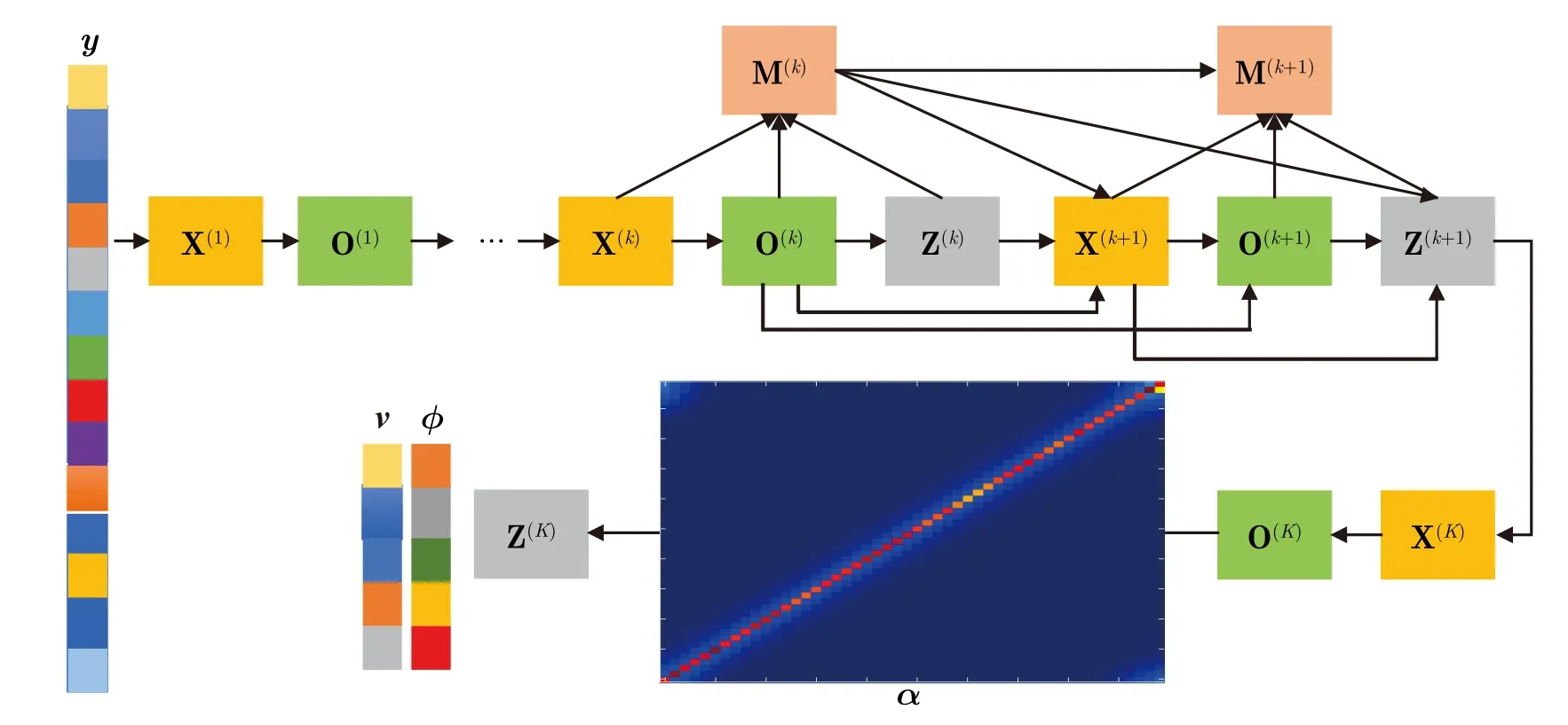
图2 ADMM算法的数据流图Fig.2 The data flow graph of ADMM algorithm

表1 ADMM算法Tab.1 ADMM algorithm

3.2 AE-ADMM-Net

对于式(13)所示的优化问题，当机载雷达参数给定且杂波复幅度、阵列误差和噪声均服从一定分布时，训练距离单元的空时回波信号yl也将具有一定分布。此外，给定空时导向矢量字典A，杂波空时谱αl也将具有一定稀疏分布。此时，可假设存在一组最优的参数序列，使得对于所有服从一定分布的空时回波信号、杂波空时谱和阵列误差，ADMM算法均能够快速准确地求解式(13)。因此，为解决ADMM算法存在的问题，结合模型驱动算法的可解释性和数据驱动深度学习方法的非线性拟合能力，本节基于ADMM算法的迭代步骤和数据流图，构建AE-ADMM-Net，将其用于求解式(13)。基于充足完备的训练数据集对AE-ADMM-Net进行训练，能够获得最优的迭代参数，从而提高杂波空时谱和阵列误差参数的估计速度和性能。下面对AE-ADMM-Net的网络结构、数据集构建方法、网络初始化与训练进行具体描述。

3.2.1 网络结构

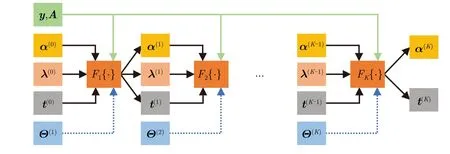
图3 AE-ADMM-Net的网络结构Fig.3 The network structure of AE-ADMM-Net

图4 AE-ADMM-Net的4个子层Fig.4 Four sub-layers of AE-ADMM-Net

3.2.2 数据集构建方法

与现有DU方法相同，本文AE-ADMM-Net是一种“模型+数据”联合驱动的SR方法，合理构建具有泛化能力的数据集是决定其有效性的关键。此外，DU方法大多采用监督学习的方式，按照提前给定的数据及其标签对网络进行训练。为了使空时回波信号、杂波空时谱和阵列幅相误差均具有一定的分布，本文构建数据集的方式可以概括为“设定雷达参数、设定杂波分布、设定阵列幅相误差分布、生成空时回波信号、划分训练与测试数据集、构造空时导向矢量字典、获得训练和测试标签集”，具体描述如下：

步骤1 对于机载雷达正侧视均匀线阵，设定载机高度H、载机速度v、阵元数M、脉冲数N、阵元间距d、波长λ、脉冲重复频率fr和距离范围[Rmin，Rmax]等参数；

步骤2 根据雷达距离分辨率将距离范围划分为L个距离单元，将每个距离单元所对应的距离环在方位角θ∈[0，π]上划分为Nc个杂波块，杂波块之间相互独立且幅度服从复高斯分布；

3.2.3 初始化与训练

网络的初始化和训练方法对AE-ADMM-Net的性能具有一定的影响，较好的初始化和训练方法能够使网络更容易达到收敛，在一定程度上避免陷入局部最优。AE-ADMM-Net的参数可根据3.2.2节中的步骤(7)进行初始化，即令ρ1:K=ρ0，γ1:K=γ0，τ1:K=τ0，δ1:K=δ0，ω1:K=ω0和ς1:K=γ0。与采用固定参数设置的ADMM算法相比，AE-ADMMNet经过训练后将在保证收敛性能的基础上，大幅提高收敛速度(即减少迭代次数)，缩短求解式(13)的时间。

4 仿真实验

本节通过仿真对基于AE-ADMM-Net的DUSTAP方法进行验证，并与基于SBL，FOCUSS和ADMM等算法的典型SR-STAP方法进行对比分析，仿真参数如表2所示。所有仿真均基于MATLAB R2020b实现，系统配置为Intel(R) Core(TM)i9-10900K CPU @ 3.70 GHz和NVIDIA GeForce RTX 2080 Ti GPU。

表2 仿真参数Tab.2 Simulation parameters

为验证所提方法在不同阵列误差条件下的性能，令阵列幅相误差的最大值 (νmax，φmax)分别等于(0，0°)，( 0.1，10°)，( 0.2，20°)和( 0.3，30°)，按照3.2.2节步骤(1)—步骤(5)所述方法构建4组不同的数据集。然后，设置ADMM算法的迭代参数为ρ0=0.5，γ0=0.01，τ0=0.04，δ0=M，ω0=0和K0=3000，按照3.2.2节步骤(6)—步骤(7)所述方法构建标签集。图5给出了不同阵列误差条件下，利用ADMM算法对某一数据进行处理得到的杂波空时谱和阵列误差参数估计，其从左到右分别对应(νmax，φmax)等 于( 0，0°)，(0.1，10°)，( 0.2，20°)和 ( 0.3，30°)的情况，从上到下分别为杂波空时谱、阵列幅度误差和阵列相位误差的估计。可以看出，基于上述固定参数，ADMM算法在不同条件下均能获得较为准确的估计结果，因此可利用所构建的数据集对AE-ADMM-Net进行训练。

图5 固定参数ADMM算法杂波空时谱和阵列误差参数估计结果(a1—a4：不同阵列误差参数下的空时谱估计结果，b1—b4：不同阵列误差参数下的幅度误差估计结果，c1—c4：不同阵列误差参数下的相位误差估计结果)Fig.5 Clutter space-time spectra and array error parameters estimated via ADMM algorithm with fixed parameters (a1—a4: Clutter space-time spectra estimation results in different array error parameters，b1—b4: Amplitude error estimation results in different array error parameters，c1—c4: Phase error estimation results in different array error parameters)

4.1 网络收敛性

本节验证AE-ADMM-Net的收敛性，并与固定迭代参数的ADMM算法进行对比分析。设置不同的网络层数K，按照3.2.3 节所述方法对A EADMM-Net进行初始化和训练(Adam算法，迭代次数为3000)，所得结果如图6所示。其中，图6(a)，图6(b)为AE-ADMM-Net在网络层数K=25时的训练NMSE和测试NMSE，图6(c)为AE-ADMM-Net和ADMM算法在网络层数(迭代次数)K=15～45时的NMSE，图6(d)为ADMM算法在迭代次数K=60～180时的NMSE。从图6(a)，图6(b)可以看出，无论是否存在阵列误差，AE-ADMM-Net的训练和测试NMSE均随着训练次数的增加而逐渐下降，且在训练1500次后基本达到收敛。从图6(c)可以看出，随着网络层数(迭代次数)的增加，AEADMM-Net和ADMM算法的NMSE均逐渐下降，但前者的NMSM远小于后者。从图6(c)，图6(d)可以看出，当ADMM算法的迭代次数为AE-ADMMNet的4倍时，两者才具有相近的NMSE。因此，可以得出结论：无论是否存在阵列误差，A EADMM-Net均能够从所构建的数据集中学习得到最优迭代参数，获得更好的收敛性能。需要说明的是：当网络层数达到一定数值(35～40)时，AE-ADMMNet就可以获得比较准确的杂波空时谱估计结果，进一步增加网络层数并不能显著提高杂波抑制性能，反而会增加运算复杂度。因此，在实际应用中，可基于不同的仿真条件对AE-ADMM-Net进行离线训练，确定可获得较好杂波抑制性能和较低运算复杂度的网络层数取值范围，再根据实际情况进行选择。

图6 AE-ADMM-Net的收敛性及其与ADMM算法的对比Fig.6 Convergence performance of AE-ADMM-Net and its comparison with ADMM algorithm

4.2 杂波空时谱

本节验证AE-ADMM-Net的杂波空时谱估计性能，并与FOCUSS算法、SBL算法和固定迭代参数的ADMM算法进行对比分析。图7给出了不同阵列误差条件下，利用不同算法对图5所对应的数据进行处理获得的杂波空时谱估计结果，其从左到右分别对应 (νmax，φmax)等 于( 0，0°)，( 0.1，10°)，( 0.2，20°)和(0.3，30°)的情况，从上到下分别对应迭代25次的ADMM算法、迭代45次的ADMM算法、迭代200次的FOCUSS算法(正则化参数设为10—3)、迭代400次的SBL算法(噪声功率初始值设为10—6)、层数为25的AE-ADMM-Net和层数为45的AE-ADMMNet。可以看出：(1)与图5相比，固定迭代参数的ADMM算法在迭代次数较少时难以获得准确的杂波空时谱估计；(2)在不存在阵列误差时，SBL算法和FOCUSS算法均能够获得杂波空时谱的准确估计，但存在阵列误差时估计性能急剧下降；(3)无论是否存在阵列误差，AE-ADMM-Net均能够基于少量网络层数(迭代次数)，实现对杂波空时谱的准确估计。因此，可以得出结论：相比典型的SR算法，AE-ADMM-Net在不同条件下均能快速获得杂波空时谱的准确估计。

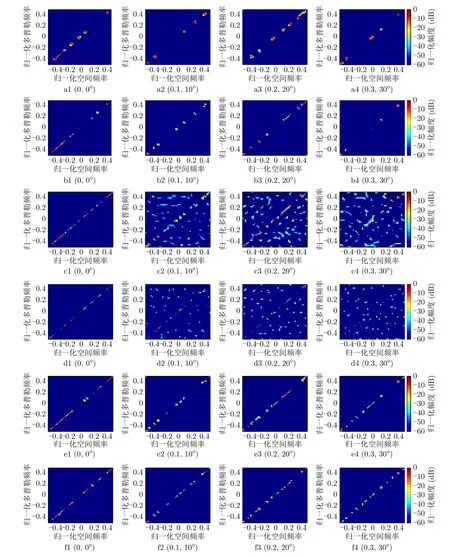
图7 不同条件下不同算法的杂波空时谱估计结果(a1—a4：ADMM算法在不同阵列误差参数下的迭代25次的估计结果，b1—b4:ADMM算法在不同阵列误差参数下的迭代45次的估计结果，c1—c4：FOCUSS算法在不同阵列误差参数下的迭代200次的估计结果，d1—d4：SBL算法在不同阵列误差参数下的迭代400次的估计结果，e1—e4：25层的AE-ADMM-Net 在不同阵列误差参数下的的估计结果，f1—f4：45层的AE-ADMM-Net 在不同阵列误差参数下的估计结果)Fig.7 Clutter space-time spectra estimated via different algorithms under different conditions (a1—a4: estimation results of ADMM algorithm with 25 iterations in different array error parameters，b1—b4: estimation results of ADMM algorithm with 45 iterations in different array error parameters，c1—c4: estimation results of FOCUSS algorithm with 200 iterations in different array error parameters，d1—d4: estimation results of SBL algorithm with 400 iterations in different array error parameters，e1—e4: estimation results of AE-ADMM-Net with 25 layers in different array error parameters，f1—f4: estimation results of AE-ADMM-Net with 45 layers in different array error parameters)

4.3 阵列误差参数

本节验证AE-ADMM-Net的阵列误差参数估计性能，结果如图8所示。图8从左到右分别对应(νmax，φmax)等 于( 0，0°)，( 0.1，10°)，( 0.2，20°)和 (0.3，30°)的情况，上图和下图分别为幅度误差和相位误差估计结果。可以看出：在不同条件下，AE-ADMM-Net均能获得阵列幅度误差和相位误差的准确估计。

图8 不同条件下AE-ADMM-Net的阵列误差参数估计结果(a1—a4：不同阵列误差参数下的幅度误差估计结果，b1—b4：不同阵列误差参数下的相位误差估计结果)Fig.8 Array error parameters estimated by AE-ADMM-Net under different conditions (a1—a4: Amplitude error estimation results in different array error parameters，b1—b4: Phase error estimation results in different array error parameters)

4.4 SCNR损失

本节验证基于AE-ADMM-Net的DU-STAP方法的杂波抑制性能，并与基于FOCUSS算法、SBL算法和固定迭代参数ADMM算法的SR-STAP方法进行对比分析。需要说明的是：由于SBL算法和FOCUSS算法无法有效估计阵列误差参数，因此在进行性能对比分析时，不考虑阵列误差参数，仅对不同算法得到的杂波空时谱进行处理，即基于式(11)估计CNCM、基于式(3)计算空时滤波器最优权值wopt。然后，利用SCNR损失衡量不同方法的杂波抑制性能，表示为

假设目标的空间频率为0(即=1M)、归一化多普勒频率在[—0.5，0.5]范围内变化，不同方法对应的SCNR损失曲线如图9所示，其从左到右分别对应(νmax，φmax)等于( 0，0°)，( 0.1，10°)，( 0.2，20°)和(0.3，30°)的情况，下图对应上图的局部放大结果。可以看出：(1)基于FOCUSS和SBL算法的SRSTAP方法仅在无阵列误差时有效，在存在阵列误差时杂波抑制性能急剧下降；(2)基于固定迭代参数ADMM算法的SR-STAP方法在迭代次数较多的条件下(ADMM-opt，K=3000)能够有效抑制杂波，但在迭代次数较少的条件下(K=25和45)，由于杂波空时谱估计不准确，其杂波抑制性能较差；(3)基于AE-ADMM-Net的DU-STAP方法基于少量网络层数(迭代次数)即可获得杂波空时谱的准确估计，实现对杂波的有效抑制，网络层数为K=45时的性能与ADMM-opt相当。因此，可以得出结论：相比典型的SR-STAP方法，DU-STAP方法在不同条件下均能获得较好的杂波抑制性能。

图9 不同条件下不同方法对应的SCNR损失曲线(a1—a4：不同阵列误差参数下的SCNR曲线结果，b1—b4：不同阵列误差参数下的SCNR曲线局部放大结果)Fig.9 SCNR loss curves corresponding to different methods under different conditions (a1—a4: SCNR loss curves results in different array error parameters，b1—b4: SCNR loss curves results with enlarged scale in different array error parameters)

4.5 运算复杂度

本节分析AE-ADMM-Net的运算复杂度，并与FOCUSS算法和SBL算法进行对比。需要强调的是：由于可以采用离线训练、在线应用的方法[25，29]，本文对AE-ADMM-Net的运算复杂度分析不包括网络训练所需的运算量。此外，在进行训练获得最优参数后，AE-ADMM-Net与ADMM算法的运算完全相同，仅在迭代参数上具有差异。因此，在网络层数(迭代次数)相同的条件下，AE-ADMM-Net与ADMM算法在应用时将具有相同的运算复杂度。以乘法次数为指标，可得不同算法进行一次迭代所需的运算复杂度如表3所示。可以看出，AE-ADMMNet的运算复杂度远小于FOCUSS算法和SBL算法。为了对此进行验证，基于MATLAB的TIC和TOC命令获得不同条件下AE-ADMM-Net，FOCUSS和SBL算法的运行时间如图10所示。其中，图10(a)对应M=N=10、Nd=Ns=50、迭代次数K=15～45；图10(b)对应M=N=4～16、Nd=Ns=50、迭代次数K=45；图10(c)对应M=N=10、Nd=Ns=20～80、迭代次数K=45；图10(d)对应M=N=Nd/5=Ns/5=4～16、迭代次数K=45。可以看出：在不同条件下，AE-ADMM-Net的运行时间均远小于FOCUSS算法和SBL算法。此外，需要指出的是：与ADMM算法相似，参数固定的FOCUSS算法和SBL算法通常也需要相比AE-ADMM-Net更多的迭代次数以达到收敛。因此，可以得出结论：相比基于FOCUSS和SBL算法的SR-STAP算法，基于AEADMM-Net的DU-STAP方法具有更低的运算复杂度。

表3 不同算法的运算复杂度Tab.3 Computational complexities of different algorithms

图10 不同条件下不同算法的运行时间Fig.10 Running time of different algorithms under different conditions

4.6 实测数据处理

本节基于Mountain Top实测数据[16]对所提DU-STAP方法的实际性能进行验证，并与基于固定迭代参数ADMM算法的SR-STAP方法进行对比分析，其中ADMM算法的参数设置与仿真实验一致，DU-STAP方法直接采用由仿真数据训练得到的AE-ADMM-Net。Mountain Top数据的阵元数为14、脉冲数为16，目标位于第147个距离单元，为与仿真相匹配，取10个阵元和10个脉冲所对应的数据进行处理。假设不存在阵元误差并设保护距离单元个数为4，基于ADMM和AE-ADMM-Net对第152个距离单元的空时回波信号进行处理，从而估计杂波空时谱、设计空时滤波器进行杂波抑制和目标检测，结果如图11所示。其中，前3个子图依次对应迭代3000次的ADMM算法、迭代45次的ADMM算法和网络层数为45的AE-ADMM-Net，第4个子图为目标检测结果。可以看出，本文所提DU-STAP方法对实测数据进行处理仍能获得较好的结果，在迭代次数相同的条件下，杂波空时谱估计和目标检测性能均优于基于固定迭代参数ADMM算法的SR-STAP方法。

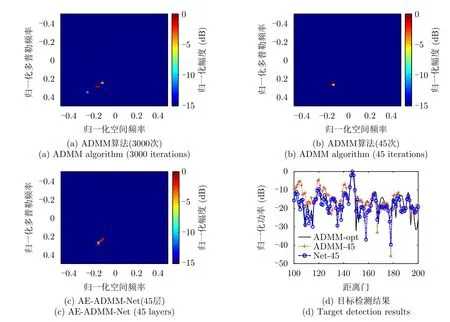
图11 Mountain Top实测数据处理结果Fig.11 Processing results of Mountain Top actual measured data

5 结语

本文提出了基于DU的机载雷达STAP方法。在存在阵列误差的条件下，对基于ADMM算法的杂波空时谱和阵列误差联合估计方法进行了分析，针对其存在的问题构建了深度神经网络AE-ADMMNet，并对其网络结构、数据集构建方法、网络初始化与训练方法进行了介绍。通过仿真实验对基于AE-ADMM-Net的DU-STAP方法进行了验证，结果表明：相比典型的SR算法，AE-ADMM-Net能够从数据中学习得到最优迭代参数，在不同阵列误差条件下快速获得杂波空时谱和阵列误差参数的准确估计；相比典型的SR-STAP方法，DU-STAP方法能够获得较好的杂波抑制性能，且运算复杂度更低。下一步将对载机偏航、距离模糊、杂波内部运动和网格失配等非理想条件下的算法改进与分析进行深入研究。