面向可见光和SAR 影像配准的特征点检测

王丽娜，梁怀丹，王中石，徐 瑞，石广丰*

（1. 长春理工大学 机电工程学院，吉林 长春 130022；2. 中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033）

1 引言

随着传感器技术的发展，传感器的种类逐渐增加。可见光传感器技术相对成熟，使得可见光图像具有成像效果好，分辨率高和易于解读等优点，但是，可见光传感器成像容易受到天气的影响。合成孔径雷达（Synthetic Aperture Radar，SAR）属于主动发出微波的成像系统，具有穿透力强、对人造目标尤其是金属目标十分敏感、能够有效地识别伪装和揭露掩盖等特点，但是，SAR 图像的可读性不如可见光图像［1-2］。将两种图像配合使用有助于形成信息互补，可应用于诸多场景，例如，图像融合，地物目标分类与识别等［3-5］。为了融合异源遥感数据实现对地观测，需要对图像进行高精度配准，而特征提取作为图像配准的前提步骤，其提取精度和特征点的重复率严重影响配准结果，因此，研究适用于可见光和SAR 图像的特征提取方法，提升特征提取精度和重复率，已成为异源遥感图像处理领域的研究热点之一。

近年来，在计算机视觉领域出现了许多特征点 检 测 算 子，典 型 的 算 子 如SIFT［6］、SURF［7］和Harris［8］等。由于可见光和SAR 图像间的非线性辐射差异和SAR 斑点噪声的影响，将常规的特征点提取算法直接用于可见光和SAR 图像提取时效果并不理想，特征点重复率较低，进而降低了配准算法性能［9］。为了克服上述问题，诸多学者在特征提取上做出改进，Ye 等学者结合了Harris-Laplace 和DOG 两种算子的优势，提出了Harris-DOG 检测算子［10］，该算子能够同时检测影像间的角点和Blob 点，为影像匹配提供更多、更稳健的特征点。Xiang 等学者对可见光和SAR图像分别采用不同的梯度计算方式，提取出可见光和SAR 图像的一致性梯度信息，在此基础上构造了两个不同的Harris 尺度空间来提取高度重复的特征点［11］。Zhang 等学者同样改进了梯度计算方式，利用多尺度Sobel 和多尺度ROEWA算子分别计算可见光和SAR 图像的梯度来获得一致性较好的梯度结果，并在此基础上进行特征点提取，有效地提高了特征点的重复率［12］。Fan等学者提出一种均匀分布的特征点检测方法UNDSS-Harris［13］，UNDSS-Harris 利 用 非 线 性 扩散滤波来构建非线性扩散尺度空间，较好地保留了边缘梯度特征；在此基础上，采用多尺度Harris算子、比例系数和分块策略，在可见光和SAR 图像中提取出均匀分布的特征点。保文星等学者提出了一种改进的基于信息熵约束和KAZE 特征提取的预处理算法［14］。该方法利用滑动窗口对整幅遥感图像进行遍历，计算出每个窗口的信息熵并形成直方图，通过阈值设定保留高信息熵以便用于特征提取。总的来说，上述方法的本质仍是基于图像梯度信息来提取影像间的显著特征，但可见光和SAR 影像间的灰度差异较大，加之SAR 斑点噪声的影响，严重影响了梯度计算结果，导致特征提取的重复率较低，进而降低了算法的匹配性能。

近年来，频域特征检测技术在异源遥感领域中的优势逐渐突显出来。比较典型的如相位一致性（Phase Congruency，PC）［15］。该方法不受光照、灰度差异的影响，可大范围的检测图像中的角点、边缘和纹理等特征［16］。鉴于PC 在特征检测方面的优势，其已成为学者们的研究热点。孙明超等学者基于相位一致性最大矩和相位一致性最小矩的叠加图进行Harris 特征点提取，获得了稳定的角点和边缘点，用于后续的特征匹配［17］。Paul 和Pati 两位学者结合Gabor 奇滤波器和 多 尺 度Harris 函 数 进 行 特 征 点 检 测［18］。Li 等学者在相位一致性最大矩和最小矩上分别进行FAST（或Harris）特征点检测［19］。

诸多学者基于相位一致性提取出影像间的同名特征，但上述方法未充分考虑影像间的非线性辐射差异和SAR 斑点噪声对特征点提取结果的影响。相位一致性在特征提取和特征描述方面尚有待发掘，算法稳定性有待提升。针对此问题，本文提出了一种基于相位一致性矩特征的Harris 特征点提取算法——MMPC-Harris。首先，对待处理图像进行包含重叠区域的分块操作，增加特征点的均匀分布特性；然后，结合相位一致性最大矩和最小矩构建相位一致性多矩图，通过Harris 算法实现特征的精细提取；最后，通过对多矩图上特征点进行投票和统计，选取重复出现超过$数的特征点作为最终的特征点。最终的特征点集合中包含了Harris 特征点和在边缘上提取的Harris 点，该方法保证了特征点的数量和稳定性。

2 相位一致性特征检测理论

相位一致性是基于频域信息进行特征提取的理论，最早由Morrone 和Owens 两位学者提出［20］。早期的相位一致性理论仅适用于一维信号，而图像为二维信号，为此，Kovesi 在该理论基础上做出了改进，将其扩展到二维，提出了二维相位一致性特征检测理论。Kovesi 采用多尺度、多方向的Log Gabor Filter 来计算图像的局部相位特征。二维Log Gabor Filter 的表达方式为：

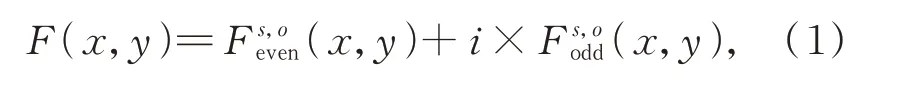
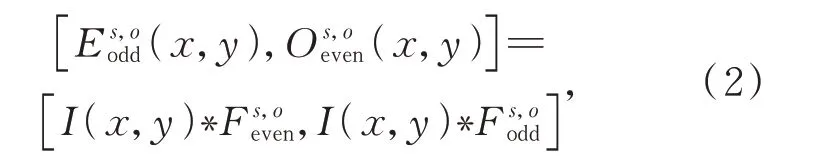
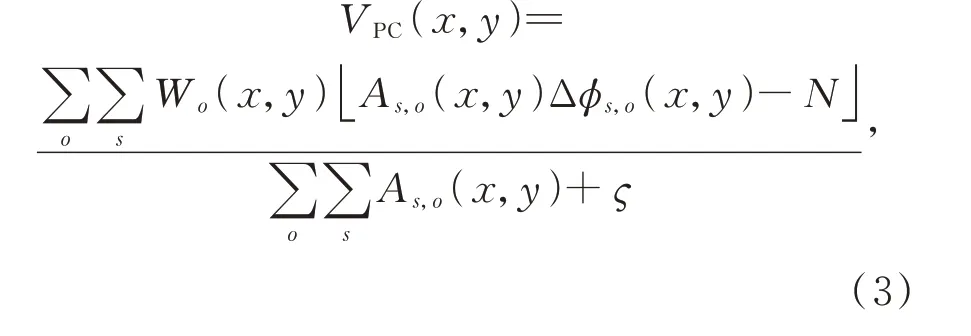
其中：Wo(x，y)为随着滤波器响应变化的加权函数；运算表示符号内代数式的值为正时，符号内的计算结果与符号内代数式的计算结果相等，否则结果为0；N表示估计的噪声阈值；ς是一个小常数，避免分母为零的情况；As，o(x，y)和φs，o(x，y)分别表示PC 的幅值和相角，计算方式如下：

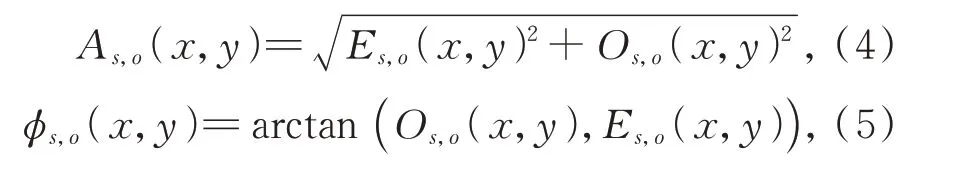
其中，Δφs，o(x，y)为相位差，计算方式如下：

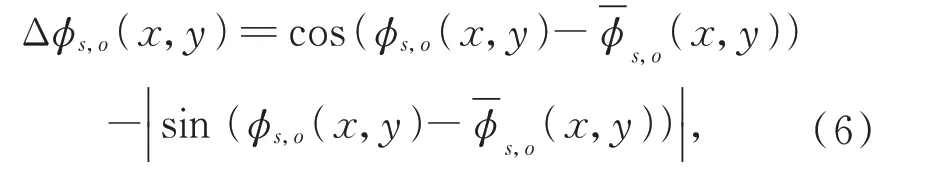
进一步，Kovesi 分析了相位一致性矩随方向变化的情况，提出利用基于相位一致性度量进行角点特征和边缘特征的检测方法［16］。Kovesi 计算任意方向o和尺度s上的PC2值来获得相位一致性的最大矩M和最小矩m，最终得到影像的角点特征和边缘特征，M和m具体形式如下：

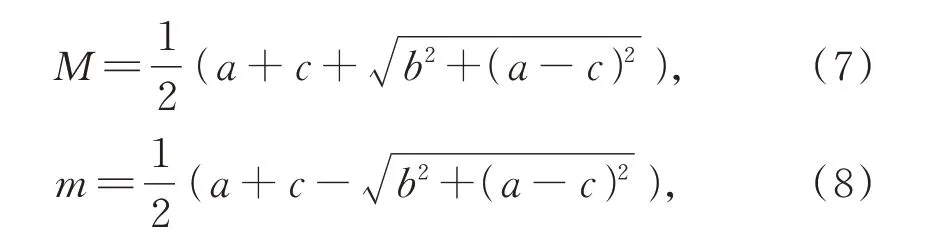
其中：a，b，c是中间变量，其具体形式如下：

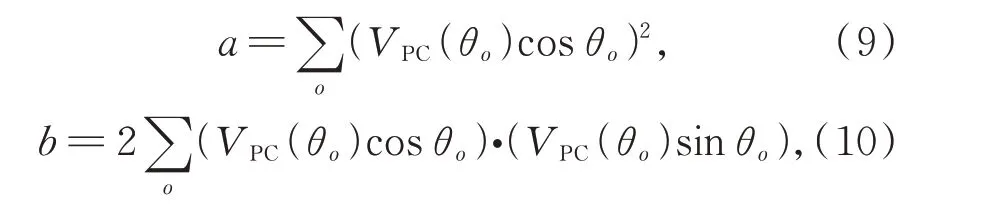
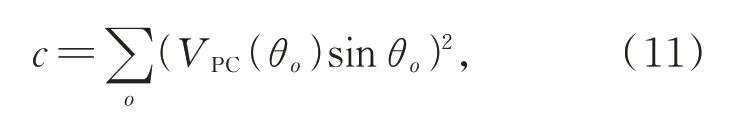
其中，θo表示方向o对应的角度。M反映了边缘强度信息，可以用于边缘特征的检测；m相当于角点检测子中的角点率，当像素点处的m值较大时，则该像素点是角点的可能性较大，通过设定m的特定阈值来筛选影像的角点特征。

3 基于改进相位一致性的可见光和SAR 影像特征提取

基于相位一致性的最大矩和最小矩信息能够获取图像的边缘和角点信息。可见，图像的相位一致性矩信息可以有效表示图像的特征。本文提出图像的相位一致性矩特征表示如下：

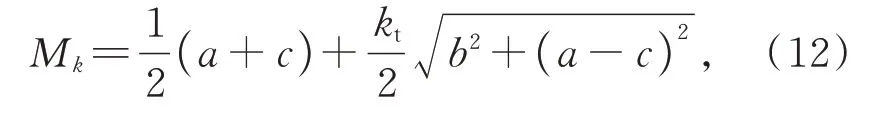
其中：a，b，c是式（9）～式（11）的中间变量，Mk表示第k个矩特征图像。进一步可以根据最大矩和最小矩特征将公式（12）描述为：

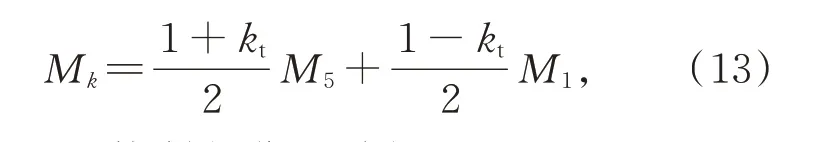
其中，kt用于控制相位一致性矩的值，取值范围为：[ -1，1]。若相位一致性多矩图数量为n，则参数kt以步长h=2n-1 变化。

可见光和SAR 影像间存在明显的非线性辐射差异，但二者的边缘相似度极高［21］，因此，考虑先提取出一致性较好的边缘特征，在边缘上进行特征点检测，来增加特征点数量。而相位一致性是一种频域特征检测理论，相比于直接利用梯度来提取边缘，能够更好地抵抗影像间的非线性辐射差异。鉴于此，本文提出了一种基于相位一致性矩进行特征提取的方法（MMPC-Harris），该方法旨在抵抗SAR 斑点噪声的影响和影像间的非线性辐射差异，来获得均匀分布且重复率较高的特征点对，进一步提升配准算法的性能。图1 给出了算法流程图。

图1 本文算法流程图Fig.1 Flow chart of the proposed method

MMPC-Harris 的具体步骤如下：

（1）分块处理：将输入图像分成Sn×Sm个图像块，并在相邻图像块之间增加nop个像素的重叠区域，以防止在分块边界处丢失特征信息；

（2）对每个图像块构建相位一致性多矩特征图。通过多次实验发现，随着相位一致性多矩图数量n的增加，特征点重复率有所提高，n超过5之后增加的速度明显变慢。综合考虑到算法的计算量，本文实验选取n=5。在每个相位一致性矩特征图像上基于Harris 提取特征点，记录特征点位置和数量。

（3）基于统计原理，投票确定最终的特征点。若某一特征点在多矩图中出现的次数超过多矩图数量的一$，则将该特征点放入最终特征提取结果的集合中，并利用其在多矩图中坐标取平均值作为最终该特征点的位置信息。

（4）将每个图像块的特征提取结果合并，构成本文算法最终的特征点提取集合。

为了便于程序实现，参数设置为n=5，h=0.5，kt表示的序列为{-1，-0.5，0，0.5，1}，给出MMPC-Harris 程序逻辑如图2 所示。

图2 MMPC-Harris 程序逻辑图Fig.2 Program logic diagram of MMPC-Harris

下面通过模拟可见光和SAR 图像进行实验分析，如图3 所示。在可见光图像上分别加入高斯噪声和斑点噪声来生成仿真数据，利用仿真图像作为待处理的可见光和SAR 图像。

由仿真结果可知，在最小矩上提取的特征点重复率较高，但容易受噪声的影响，出现了一定的错误点对，如图3（b）。在最大矩上提取的边缘点的数量较多，能够保证特征点数量，如图3（f）。将两者直接相加作为最终的特征点集，尽管结果中含有稳定的角点和数量较多的边缘点，但仍存在一定问题，如直接叠加方式难以抵抗噪声干扰，导致结果中仍存在一些不稳定的特征点，如图3（g）。而本文算法基于相位一致性多矩特征和统计原理来获得最终的特征点，以此来抵抗噪声干扰，剔除了虚假点，进而得到稳定的特征点对，保证了特征点的重复率；再加上分块处理，获取均匀分布的特征点，如图3（h）。

图3 不同相位一致性矩特征的Harris 检测结果Fig.3 Harris detection results of different PC feature

4 实验与分析

本小节对MMPC-Harris 特征点检测算子的性能进行实验分析，实验内容包括三个部分：首先，验证MMPC-Harris 特征点检测算子对SAR斑点噪声的鲁棒性；其次，验证MMPC-Harris 特征点检测算子对非线性辐射差异的鲁棒性；最后，基于一组实测可见光和SAR 图像验证MMPC-Harris 特征点检测算子对整体配准算法性能提升的影响。

4.1 MMPC-Harris 对噪声鲁棒性评估

4.1.1 实验数据

目前尚且没有公开的可见光和SAR 数据集用于测试特征点检测算法的优劣。为了便于计算特征点重复率，验证本文算法的有效性，本小节实验部分仍采用仿真数据，仿真数据的生成方式为对高清可见光图像分别加高斯噪声和不同级别的斑点噪声来生成仿真可见光和SAR 图像，原始高清光学图像如图4 所示。

图4 高清可见光图像Fig.4 High resolution optical images

高清图像为长光卫星科技公司拍摄的智利圣地亚哥的机场和港口，拍摄时间为2017 年3月，影像分辨率为1 m/pixel，图像大小均为1 000 pixel×1 000 pixel。对上述两组高清光学图像分别加入高斯噪声和乘性噪声所生成仿真光学和SAR 图像，结果如图5 所示。

图5 两组模拟图像（左侧为可见光图像，右侧为SAR 图像，L=5）Fig.5 Two sets of simulated images（The left are optical images and the right are SAR images，L=5）

4.1.2 评价方法和评价准则

为验证本文算法的先进性，选取了典型的特征 点 检 测 算 法Harris［8］，SAR-Harris［21］和m+MHarris［17］作为对比算法。通过定性和定量两种方式来评价算法的性能。定性分析通过观察特征点的分布情况，均匀分布的特征点有利于几何变换模型的求取。定量分析则以不同SAR 噪声级别下，特征点重复率R作为评价指标。参考图像A和待配准图像B上的一对特征点属于同名点前提为：

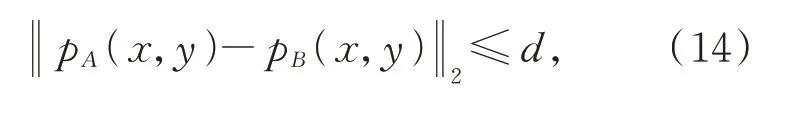
其中：pA(x，y)和pB(x，y)分别表示特征点在参考图像和待配准图像中的位置坐标，符号‖ ‖·2为欧式距离测度，d为欧式距离阈值。本文d设置为2，表征若两点之间的欧式距离≤2 个像素，则这两个点为一对同名点。R定义为：

其中：Ncor为正确匹配点对数，No和Ns分别为在可见光和SAR 图像中提取的特征点总数量，R值越大，特征点检测算子的性能越好。

4.1.3 实验结果与分析

本实验通过调整阈值，使得所提取的特征点总数量保持一致，每种算法均提取约600 对特征点，取10 次计算的平均值作为最终实验结果，以减小误差的影响。图6 给出了四种算法对两组图像的特征点重复率变化曲线。

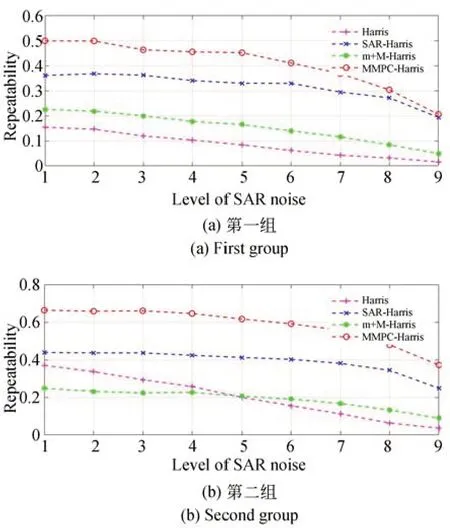
图6 特征点重复率曲线Fig.6 Repeatability rate curve of feature points

由结果可见，MMPC-Harris 在任何SAR 噪声级别下的特征点重复率均获得了最高值，说明MMPC-Harris 能在一定程度上抵抗SAR 斑点噪声的影响，获得较高的特征点重复率。SARHarris 的效果弱于本文方法，但优于Harris 算法，这是由于SAR-Harris 是在ROEWA 算子提取SAR 信息的基础上进行的Harris 特征提取，ROEWA 可以有效地抵抗SAR 斑点噪声，获得较为理想的边缘特征，因此，在此基础上进行Harris 特征提取能够抵抗噪声干扰。但是，SARHarris 仅考虑了在SAR 图像上进行特征提取所遇到的问题，并未对可见光和SAR 这两种图像的异源性进行处理，所以，效果略差于本文方法。Harris 算子的性能是最差的，随噪声水平的增加，特征点重复率值下降较快，表明Harris 算子容易受到SAR 乘性噪声影响，不适合用于直接处理SAR 图像。

4.2 MMPC-Harris 对非线性辐射差异的鲁棒性评估

4.2.1 实验数据

对图4（a）的列乘以可变系数来模拟影像间的非线性辐射差异，结果如图7 所示，由图可见，影像间的同名特征呈现出不同的灰度特性，这种差异增加了同名特征提取的难度。

图7 模拟非线性辐射差异的图像Fig.7 Simulated nonlinear radiometric differences images

4.2.2 实验结果与分析

对比算法和评价指标同4.1 节实验一致。选取第一组实验数据的特征提取结果进行对比，结果如图8 所示。

Harris 和SAR-Harris 算子的特征提取结果分别如图8（a）和图8（b）所示，二者基于灰度梯度信息进行特征提取，易受到影像间非线性辐射差异的影响，在可见光图像中可以检测到的特征在模拟的非线性辐射差异的图像中未被检出，特征点分布不均匀，较容易集中在灰度差异较大的区域。图8（c）和图8（d）分别给出了m+M-Harris和MMPC-Harris 的特征提取结果，二者均能克服影像间的非线性辐射差异，特征点分布较均匀，在光学图像中提取的特征，在对应图像上仍然能够被检测到，这是因为本文方法和m+MHarris 方法是基于PC 进行提取的，而PC 算子对灰度和光照变化不敏感。进一步给出定量分析的结果来验证本文算子的性能，如表1 所示。

表1 四种算法在非线性辐射差异情况下的重复率Tab.1 Repetition rates of the four methods in the case of nonlinear radiometric differences

图8 四种算法特征点提取结果Fig.8 Feature point extraction results of four algorithms

四种算子中，MMPC-Harris 的特征点重复率值最高，这是由于本文方法在相位一致性多矩图上进行投票，剔除了一些不稳定的特征点，故本文算子可以较好地抵抗影像间的非线性辐射差异的影响，获得更多的同名点对。

4.3 MMPC-Harris 特征点检测算子的配准性能

MMPC-Harris 可以提升特征点的重复率，进而提升配准算法性能。为了证实这一点，基于一组实测的可见光和SAR 图像进行配准实验，选取 了Harris、SAR-Harris 和m+M-Harris 特 征 点检测算子作为对比算法，所有描述符均采用HOSMI［22］，以 验 证MMPC-Harris 特 征 点 检 测 算子对可见光和SAR 图像配准性能的提升。

4.3.1 实验数据和评价指标

实验数据如图9 所示，左侧为在Google Earth 上截取的同一地区的可见光影像，右侧为机载SAR 影像，拍摄时间为2017 年7 月。可见光和SAR 图像的尺寸均为1 741 pixel×1 075 pixel，分辨率为3 m/pixel。拍摄场景为郊区，包含河流、低矮建筑物、农田和道路等。

图9 可见光和SAR 影像Fig.9 Optical and SAR images

配准实验采用主观和客观两种评价方式。主观评价方式为直接给出配准结果，客观评价指标为均方根误差（Root Mean Square Error，RMSE）和正确匹配点对数（Number of Correct Matches，NCM）。通过调整阈值，使得本文方法和对比方法均提取约1 200 对特征点。采用平方差之和（Sum of Square Differences，SSD）作为匹配准则，SSD 阈值设置为3 个像素，并利用FSC［23］剔除误匹配。

4.3.2 实验结果与分析

利用四种检测算子的特征提取结果进行配准，结果如图10 所示，表2 显示了四种检测算子的NCM 和RMSE。

表2 四种方法的NCM 和RMSETab.2 NCM and RMSE of the four algorithms

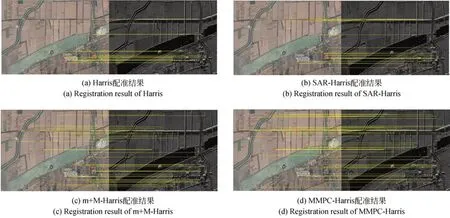
图10 四种算法的配准结果Fig.10 Registration results of four algorithms

由配准结果可见，四种检测算子都能完成配准，但配准性能存在差异。Harris 和SAR-Harris是直接利用灰度信息进行特征提取的，所获得的正确匹配点对分布不够均匀，这说明直接利用灰度信息进行特征提取难以抵抗影像间的非线性辐射差异。m+M-Harris 和MMPC-Harris 均取得了较好的效果，这说明基于PC 进行特征提取有助于抵抗影像间的非线性辐射差异。

结果表明，与其他特征点检测算子相比，在描述符一致的情况下，MMPC-Harris 获得了最多的NCM 和最小的RMSE，这是因为MMPC-Harris 是基于PC 特征进行特征点检测的，在一定程度上抵抗了影像间的非线性辐射差异，同时，MMPC-Harris 检测了角点和边缘上角点，保证了特征点的数量，通过建立相位一致性多矩图和设计的投票策略，在一定程度上剔除了噪声的影响，从而获得大量稳定特征点用于图像匹配。此外，MMPC-Harris 使用了分块策略，能够获得均匀分布的同名点对，可以更好地适应影像间的几何形变。总之，MMPC-Harris 可以显著提高在可见光和SAR 影像间所提取的特征点重复率，进而提升配准精度。

5 结论

本文针对可见光和SAR 影像间的非线性辐射差异和SAR 斑点噪声导致在影像间提取的特征点重复率较低的问题，提出了一种基于相位一致性的特征点提取算法MMPC-Harris。MMPCHarris 通过计算图像的相位一致性矩信息，构建了相位一致性多矩图，在所构建的相位一致性多矩图上提取Harris 角点，并设计了投票策略，选取了重复出现超过$数的点作为最终的特征点，获得了稳定的角点和边缘点。仿真数据的测试结果表明，MMPC-Harris 可以较好地抵抗影像间的非线性辐射差异和SAR 斑点噪声的影响，有效地提高了特征点的重复率。一组实测可见光和SAR 图像上的测试结果表明，与其他三种方法对比，MMPC-Harris 的正确匹配点对数分别提高了23、26 和35 对，均方根误分别降低了12.6%、37.2%和40.8%，能够有效地提升配准算法性能。但是，MMPC-Harris 不具备旋转和尺度不变性，下一步工作将针对此问题进行更加深入地研究。