Direct measurement of two-qubit phononic entangled states via optomechanical interactions

A-Peng Liu(刘阿鹏) Liu-Yong Cheng(程留永) Qi Guo(郭奇)Shi-Lei Su(苏石磊) Hong-Fu Wang(王洪福) and Shou Zhang(张寿)

1Shanxi Institute of Technology,Yangquan 045000,China

2School of Physics and Information Engineering,Shanxi Normal University,Taiyuan 030032,China

3College of Physics and Electronics Engineering,Shanxi University,Taiyuan 030006,China

4School of Physics and Engineering,Zhengzhou University,Zhengzhou 450001,China

5Department of Physics,College of Science,Yanbian University,Yanji 133002,China

Keywords: entanglement measurement,phononic qubit,optomechanical system

1. Introduction

Entanglement plays a vital role in quantum physics because of its applications in quantum information science and testing the fundamental principles of quantum mechanics.[1–4]As the earliest proposed two-qubit entangled states, Bellstates, which violate the locality inequalities at the extreme,have great significance for the quantum information processing (QIP) because more entanglement means a better performance(a higher success probability or fidelity). Therefore,in most of early research, the maximally entangled pure states,such as Bell states,attracted a great deal of attention.[5,6]Nevertheless,owing to the ambient noise,a Bell state is easy to be disturbed and eventually degenerates to a nonmaximally entangled state or even a mixed state. It is natural to consider realizing QIP with specific nonmaximally entangled states. Recent research on the nonmaximally entangled states as fundamental physical resources have found some interesting applications in QIP tasks. More and more research on nonmaximally entangled pure states or mixed states are invested.[7–10]Specifically,under the influence of external environment,typical maximally entangled Bell states might become nonmaximally entangled Bell-like states, or mixed states, e.g., the Werner states[10,11]or the Collins–Gisin states.[12,13]Since different degrees of entanglement can have different potential applications,to quantify the various entangled states is of important significance in QIP applications.

There have been several methods to quantify an entangled state, such as Bell inequalities,[14]logarithmic negativity,[15]Duan criterion,[16]entanglement witnesses[17]and quantum state tomographic reconstruction.[18]For an entangled state whose compositions are known, its entanglement can be calculated by the state parameters,regardless of which entanglement measure criterion is adopted. But for an entangled state with unknown parameters, a method named entanglement of formation (EOF), which was introduced by Bennettet al. in 1996, could be one alternative way for its easy-to-operate feature.[9,19]Based on EOF,Wootterset al.[20,21]proposed an exactly calculable quantity, i.e., concurrence, to quantify the entanglement of an arbitrary two-qubit stateρ12. According to Ref.[20],there is an explicit formula for concurrence as

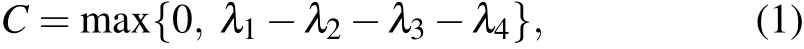
whereλi(i=1,2,3,4) are the square roots of the eigenvalues of the operatorρ12(σy1⊗σy2)ρ∗12(σy1⊗σy2) in decreasing order.[21,22]In recent years,a number of theoretical and experimental schemes have been presented for direct measurement of concurrence for two-qubit entangled states,[23–28]including pure states and mixed states. So far,most existing studies paid attention to measurement entanglement for atomic entangled states with cavity quantum electrodynamics system[29–33]or photonic entangled states with optical elements.[34,35]

In recent years, mechanical resonators are considered as important platforms for performing QIP tasks owing to their unique features, such as low-dissipation, tunable coupling to other quantum systems.[36,37]Optomechanical system,[36–47]a composite structure of mechanical resonators,has been applied to QIP tasks such as storage,[48]sensors,[49]transducers,[50]entanglement generation[51,52]and entanglement concentration.[53]Compared to photons, phonons move much slowly, and consequently, they are more apposite for storing and transferring quantum information.Recent research showed phonons of quantized mechanical vibration modes can be confined in mechanical resonators[54,55]and propagate in phononic waveguides.[56]Besides, with the help of phononic crystal, the mechanicalQ-factor can be effectively enhanced.[54,55]These new progresses pave the way for realizing the applicable QIP tasks with optomechanical systems.

In this paper, we put forward schemes of directly measuring concurrence for two-qubit phononic entangled states,including two-qubit nonmaximally entangled Bell-like states,the Werner states and the Collins–Gisin states.In our schemes,since phonons cannot be operated as photons, the original phononic entangled states are measured with the help of cross-Kerr nonlinearity in an optomechanical system. Firstly,combining the cross-Kerr optomechanical systems and a Mach–Zehnder interferometer, we propose a scheme for measuring phononic Bell-like state with the aid of optomechanical nonlinear interactions. As a result of this concurrence measurement scheme, a nonlocal four-phonon maximally entangled state is shared between two spatially separated participants.Furthermore,by postselecting the odd parity state of phonons,we present the direct measurement schemes for two classes of two-phonon mixed states,Werner states and Collins–Gisin states. Finally, we analyze the influence of less-than-ideal experimental parameters and evaluate the feasibility of our schemes.

2. Cross-Kerr optomechanical system

We consider an optomechanical system to realize a cross-Kerr optomechanical interaction between the photon and the mechanical oscillator.[57–59]Here a membrane mode (denoted asb′with frequencyωm′) is quadratically coupled to a Fabry–P´erot cavity mode (denoted ascwith frequencyωc)with the “membrane-in-the-middle” configuration, as shown in Fig.1. The cavity couples with the mechanical membrane with strengthg. The mechanical membrane tunneling couples to the target mechanical oscillator(denoted asbwith frequencyωm) with strengthV, and this interaction can be realized by a resonator interacting with a transmission line resonator via a capacitanceC.[60]Under the conditionωm′≫g,b′2andb′†2can be ignored by rotating wave approximation.Meanwhile, when the dissipation rate of mechanical oscillators is weak enough and the dynamic time of the oscillators is much smaller than that for cavity field,we can regard photon numberNcas independent of timetin the phonon evolution period. Under the weak driving condition,the occupation number of the system is rather small. Besides,we consider the dissipation of the mechanical membrane is much larger than that of the target mechanical oscillator. As detailed in the Appendix of Ref.[57],under these conditions,one can obtain the effective interaction between the optomechanical cavity and the oscillator modebas

Fig. 1. Schematic illustration of an optomechanical system consists of a membrane quadratically coupled to an optical cavity mode. The membrane is in the middle of the cavity and interacted to the target mechanical oscillator through the medium of capacitance C.

3. Direct measurement of nonlocal two-phonon entangled Bell-like states

In this section,we show the process for measuring nonlocal phononic Bell-like states. This kind of states might decay from an initial maximally entangled Bell state since the atmospheric turbulence or fibre birefringence in the entanglement distribution process. As shown in Fig.2,four mechanical oscillatorsa1,b1,a2,andb2 are coupled to four cavitiesA1,B1,A2,andB2,respectively.Initially,assume two participants Alice and Bob share two pairs of entangled oscillator modes(a1,b1)and(a2,b2)with the form

with|ψ〉the nonmaximally entangled Bell state in Eq.(5). At timet=(2n+1)π/geff,the maximal probability is

From Eq. (7), one can see that by performing an orthogonal postselection with the photon state, the state with oscillator modesa1 anda2 in odd parity is postselected. What’s more,the single-photon detection projects the phonons to a fourqubit maximally entangled state, which makes it possible to carry out other subsequent phonon-based quantum QIP tasks.

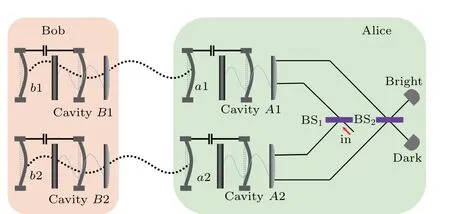
Fig. 2. Schematic of direct concurrence measurement scheme for twophonon Bell-like state. aj (bj) (j =1, 2) are four mechanical oscillators.The dotted wavy lines indicate the initially entanglements between the oscillator modes. BS is a beam splitter which splits the photon pulse into two spatial modes at equal probability. BS2 together with BS1 and two cavities constitute a Mach–Zehnder interferometer.

That is,the concurrence of the initial phononic entangled state|ψ〉can be obtained by the relevant detection probability of the single-photon state. Besides, this concurrence measurement scheme for Bell-like state|ψ〉should be also applicable for the other three ones.

4. Direct measurement of two-phonon entangled Werner states

In an actual physical situation,because of ambient noise,a maximally entangled Bell state could easily decay into a Werner state, which therefore will inevitably be faced by researchers in practical QIP tasks. From now on, we design the single-copy direct entanglement measurement scheme of an unknown Werner state. The density operator of a common two-qubit Werner state takes the form

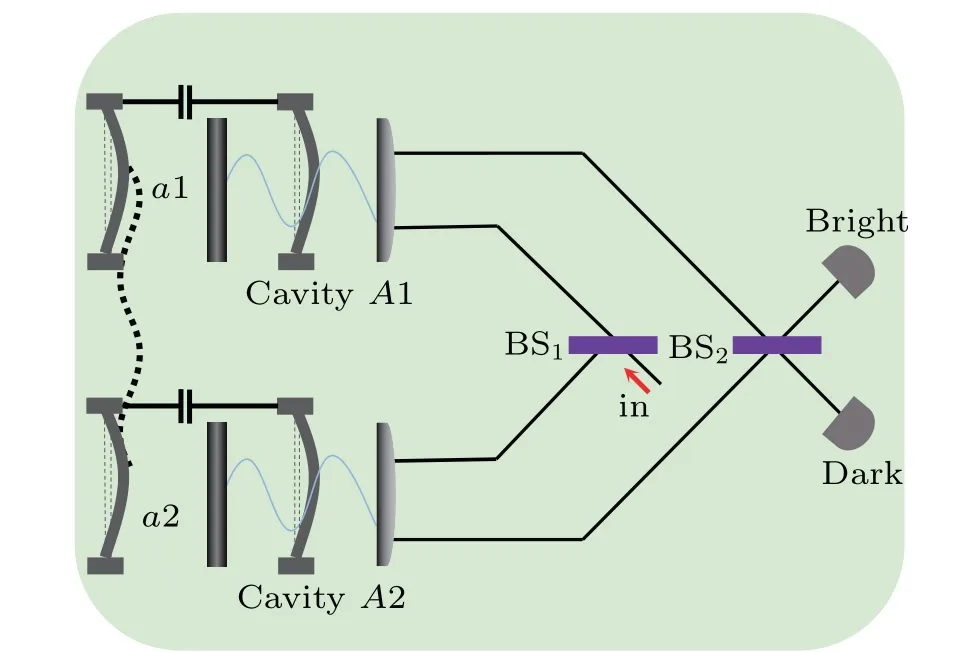
Fig. 3. Schematic of single-copy entanglement measurement scheme for phononic Werner states. The wavy dotted line represents entanglement between phonons.

We now explore the entanglement measurement of mechanical oscillators’Werner states with single-photon pulse as auxiliary, as depicted in Fig. 3. The initial state of the entire system can be expressed as|1〉in〈1|⊗ρW, which consists of five components. After the photon split by the inner beam splitter BS1, according to the cross-Kerr nonlinearity process described in Eq. (4), each component of the initial system evolves as

So far, we have accomplished the direct entanglement measurement of unknown two-qubit phononic Werner state with one copy initial state and an auxiliary photon pulse. As it should be, this scheme is also applicable to other parallel Werner states when|φ〉is replaced by other Bell states.

5. Direct measurement of two-phonon Collins–Gisin states

As shown in Fig. 4, single-photon pulses 1 and 2 are introduced by Alice and Bob respectively. Similar to the discussions in Eqs.(6)and(7),if the two photons are both detected at the dark port after the outer beam splitters BS2and BS4,one component of the photon–phonon composite system evolves as

While the other components|ψ〉a1b1|01〉a2b2,|01〉a1b1|ψ〉a2b2and|01〉a1b1|01〉a2b2will not result in dark port detection on both participants. So the coincidence dark port detections will collapse stateρa1a2b1b2into a nonlocal four-qubit GHZ state

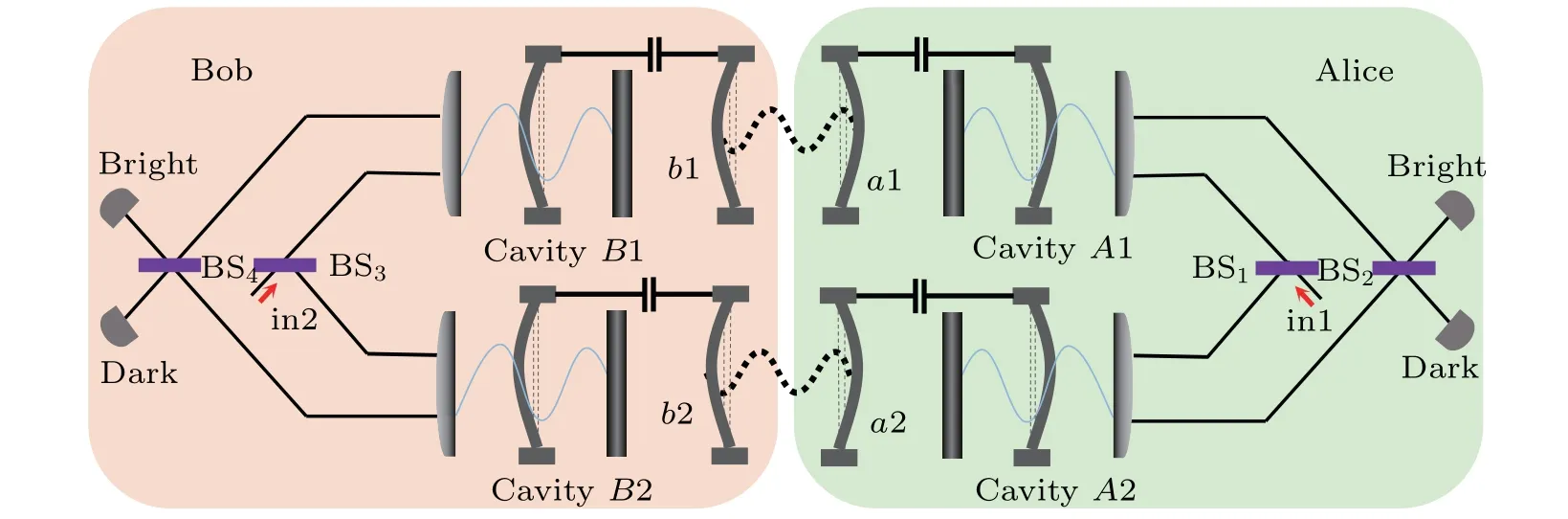
Fig.4. Schematic of direct concurrence measurement scheme for a class of two-qubit phonon mixed state,the Collins–Gisin states. The wavy dotted lines represent entanglements between phonons.

So far, as shown in Figs. 2–4, we have designed different schemes for measuring concurrence of different phononic entangled states. Therefore, in the case of knowing the types of entangled states, we can choose a pertinent measurement scheme for concurrence measurement.

6. Analysis and discussion

In the presented schemes, since the quantum nondemolition operation for phonons is difficult, phononic entanglements are measured with the aid of photon pulses via photon-phonon cross-Kerr nonlinearity interactions. Recent investigations have confirmed this controllable photon–phonon cross-Kerr nonlinearity via optomechanical interaction with high fidelity.[57]In the quadratically coupled optomechanical system, the optomechanical oscillator can be realized by a suspended film bulk acoustic resonator with∼GHz frequency[61]and the target oscillator by nanoobjects with∼MHz frequency.[62]Meanwhile the interaction between them can be controlled by LC circuits and piezoelectric ceramics.[60,61]Besides,the coefficientsωm,effandgeffare affected by the frequency difference between two oscillators|ωm′−ωm|and mechanical coupling rateV.[57]The effective frequency of the mechanical oscillatorωm,effcan also be decreased by adjusting|ωm′−ωm|, andgeffdecreases with increasing of|ωm′−ωm|. Although{ωm′,ωm} ≫V,g, one can keep|ωm′−ωm|small so that effective Kerr nonlinearity will be large. What is more, phonon entanglement is generated with quantized mechanical vibration modes, and, on this subject, there are already some theoretical schemes[51,53]and experimental realizations.[63,64]For example,Riedingeret al.[64]reported experimental generation of entanglement between two remote micromechanical oscillators by an optical field. Besides,in Ref.[53],they detailed a theoretical scheme for the preparation of a maximally entangled Bell state between two mechanical oscillators with the help of two lowenergy pump pulses and single photon detection.

Moreover, the Mach–Zehnder interferometer is used for postselecting two-phonon maximally entangled states by detecting the output photon at the dark port of a beam splitter.For the sake of estimating the probability of a successful postselection,we can use the quantity the photon arrival probability density,which can be calculated with the formula[65]

whereκis the decay rate of the cavity. The photon arrival probability density against dimensionless arrival timegefft/2πis plotted in Fig.5,from which it can be seen thatωm,eff≥90κis requested to observe oscillations of the arrival rate in an optomechanical cavity. Besides, the noises from the dark count rate would decrease the success probability of our schemes,so resolved-sideband regime should be satisfied for the schemes.In our schemes, as the window for detectors receiving photons is approximately 1/κ,|αβ|2≥3.184×10−8should be satisfied when considering a state-of-the-art silicon avalanche photodiodes with a dark count rate of∼2 Hz.[53]In addition,an efficient source with 10000 high quality single photons per second ensures our schemes can be accomplished within the valid duration.[66]

Fig.5. Probability density of a photon count vs. arrival time scaled by geff/2π for a successful postselection in the sideband-resolved regime ωm,eff = 10κ (solid red line), ωm,eff = 90κ (dashed blue line), and ωm,eff = 170κ (dotted green line). Here ωm,eff = 2 GHz, geff =0.033ωm,eff.

Fig.6. The deviation of the actually obtained concurrence of Bell-like state from the ideal one(a)∆C1 and(b)the ratio ∆C1/C as a function of coefficient α and reflection coefficient of the beam splitters γ.

We should note that, in the present schemes, suboptimal beam splitters will affect the performance of the parity check process. For example,in the scheme for measurement of Belllike states in Fig.2,if we consider two common beam splitters with the reflection coefficientγ, once the dark port detector fires,the final state of the system can be derived as

|Ψ〉′2=αβ[(1−γ)e−i(θ01+θ10)−γe−iθ11]|0101〉a1a2b1b2measurement of the Collins–Gisin states. From Eq. (19), the detection probability increases with the rise of the mixing proportion parameterf. Because the calculated concurrence relies on the probability of dark port detection on both participants,and the conclusive components corresponding to this detection result exist in the first term of Collins–Gisin states, we can decrease the deviation between the actual concurrence and the ideal concurrence by decreasing the proportion of the first term,and vice verse.[31,33]

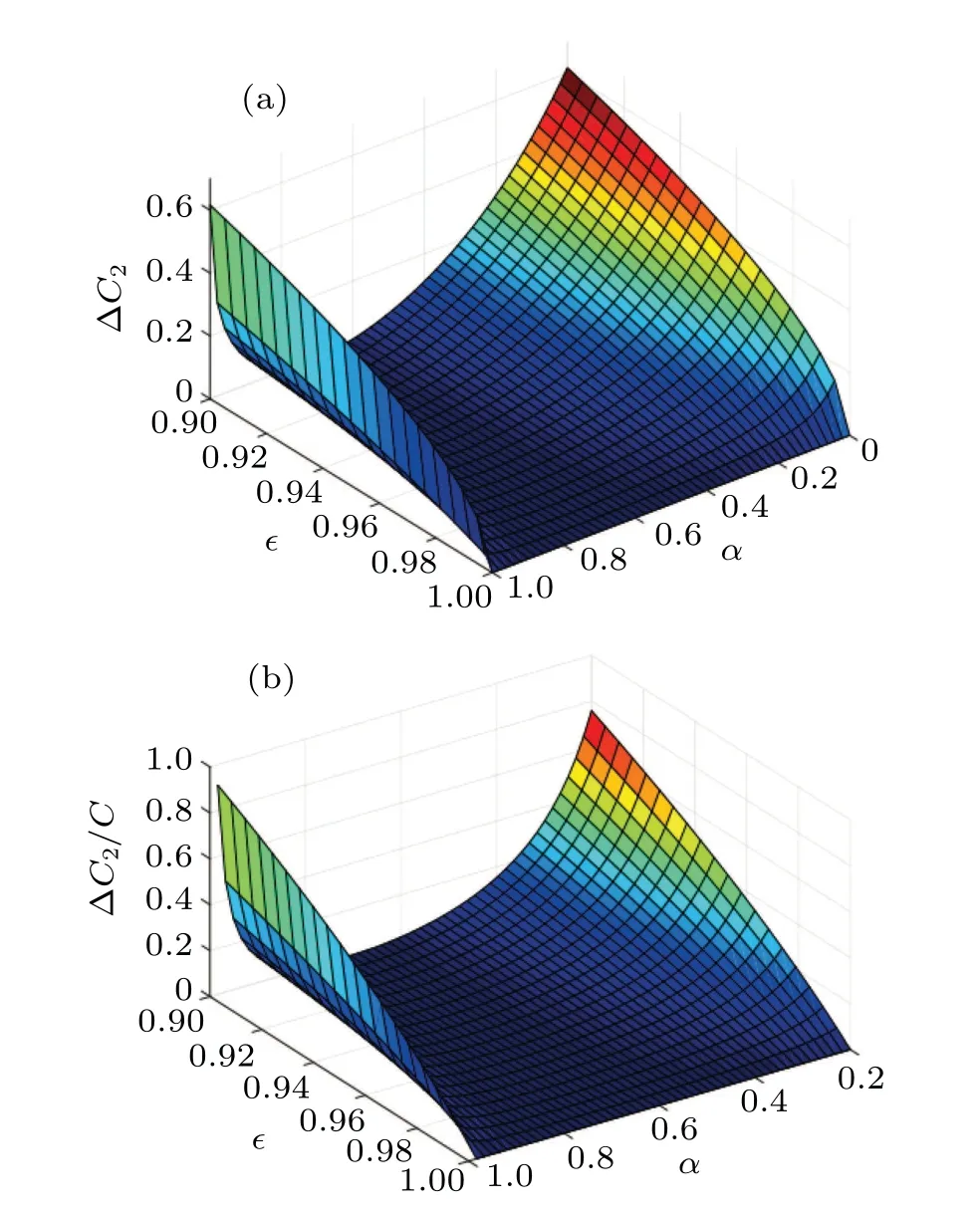
Fig.7. The deviation of the actually obtained concurrence of Bell-like state from the ideal one(a)∆C2 and(b)the ratio ∆C2/C as a function of coefficient α and scale factor ∊.

Recently, several schemes for directly measuring concurrence of atomic entanglements[30–33]and photonic entanglements[23]have been proposed. In those schemes,two copies of initial entanglement and Bell-state analysis are needed. Different from Refs.[30–33],in the present schemes,the photon interacts with two cavities simultaneously but in sequence, so our schemes work in a parallel style rather than a cascaded one. Meanwhile, strict controlled-phase-flip gate is not needed in the present schemes, therefore the values of the effective frequencies for the cavity (ωc,eff) and mechanical oscillator (ωm,eff) are not strictly required. Meanwhile,like most existing schemes, the quantity of entanglement is structured by detection probabilities of certain states of incident photons in the present schemes. Therefore,although the detection probabilityPis time-dependent, we should use the maximal successful probabilityPmaxto get the genuine concurrenceCin Eqs. (12), (17) and (23). Meanwhile, for the sake of getting the maximal successful probabilityPmax, we should know the effective nonlinear coupling strengthgeffand detect the output photon at timet=(2n+1)π/geff. Besides,in a practical experiment,we should perform the entanglement measurement process many times to obtain the maximal success probabilities to calculate the concurrence. At the same time, we should emphasize that it is still a challenge to generate two almost identical copies of the same phononic entanglement,and the post-selection measurement will decrease the efficiencies of the present schemes. Therefore,although great progress has been made in experiments,more advanced techniques are expected for practical entanglement preparation of nonlocal mechanical oscillators. It should note that,there are other entanglement measurement methods,for example,Logarithmic negativity[15]and Duan criterion,[16]which are sufficient conditions for estimating entanglement of any two-party states. However, in our schemes, we should design appropriate quantum devices and operations to obtain the concurrence of entanglement by using the detection probabilities of certain states of incident photons. Therefore, the presented schemes are not applicable for measurement the Logarithmic negativity and Duan criterion.

7. Summary

In summary, we proposed several schemes of phononic entanglement measurement for the Bell-like states, Werner states and Collins–Gisin states. Based on the optomechanical cross-Kerr interaction,we perform measurement by detecting the output photon at the dark port of the Mach–Zehnder interferometer. In virtue of the optomichanical interaction and orthogonal postselection on the output photons, the original systems collapse to phononic maximally entangled states shared by remote users instead of being completely destroyed.The analyses suggest that our schemes maybe feasible in the near future and these schemes show promising applications for phonon-based QIP tasks.

Acknowledgements

Project supported by the National Natural Science Foundation of China(Grant Nos.61801280,11604190,11747096,11804308, and 61465013), the Science and Technologial Innovation Programs of Higher Education Institutions in Shanxi Province,China(Grant Nos.2019L0988 and 2019L0043),the Fund for Shanxi “1331 Project” Key Subjects Construction(Grant No. 2019XF-04), and the Applied Fundamental Research Project of Yangquan(Grant No.2019G24).