基于VMD和PSO-SVR的短期电力负荷多阶段优化预测
2022-08-31李文武石强李丹胡群勇唐芸梅锦超
李文武,石强,李丹,胡群勇,唐芸,梅锦超
(1. 三峡大学 电气与新能源学院,湖北 宜昌 443002;2. 梯级水电站运行与控制湖北省重点实验室(三峡大学),湖北 宜昌 443002;3. 广东电网有限责任公司中山供电局,广东 中山 528400)
0 引言
电力负荷预测在电网系统规划和运行方面发挥着重要的作用。短期负荷预测作为负荷预测的重要组成部分,其常用的预测方法可概括为3大类:数理统计模型、人工智能算法和组合预测模型[1-2]。数理统计法的理论基础较强,模型建立较为简单[3]。机器学习和深度学习等为代表的人工智能算法自我学习能力较强,对模型和数据具有很好的适应性。反向传播网络(back propagation,BP)、支持向量回归(support vector regression,SVR)和长短时记忆网络等模型在短期电力负荷预测等应用中取得了较好的效果[4]。文献[5]提出了具有遗传算法(genetic algorithm,GA)的预测模型,有效提升了短期电力负荷预测的精度。然而,实际负荷序列的非线性和随机性较强,给短期负荷的可靠预测造成了困难。
目前主要采用小波变换、经验模态分解(empirical mode decomposition,EMD)、集成经验模态分解(ensemble empirical mode decomposition,EEMD)、带自适应噪声的完全集成经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN)和变分模态分解(variational mode decomposition,VMD)等信号分解技术对原始电力负荷数据进行预处理,明显改善了模型的预测性能[6-8]。文献[9]提出了模糊逻辑与小波变换相结合的广义神经网络短期负荷预测。文献[10]采用了SVR进行短期负荷预测,获得了更高的预测精度。文献[11-12]提出了短期负荷区间预测模型,所得到的预测效果优于采用EMD分解的模型。文献[13]有效改良了基础模型的性能,提升了负荷预测的精度。文献[14]采用相空间重构法(phase space reconstruction,PSR)优化模态分量序列,改善了预测效果。文献[15]提出2阶段分解模式和支持向量机的多阶段优化策略,取得了较好的预测效果。
本文提出了一种多阶段优化的短期负荷预测模型,并对比传统模型和其他模态分解方法,结合预测误差进行分析,检验所提模型的准确性。
1 多阶段优化理论基础
作为一种技术成熟且理论完备的信号分解技术,变分模态分解有效避免了EMD和EEMD等方法在分解过程中存在的模态混叠和端点效应等情况,可以获得更加平稳的信号序列[14-16]。采用VMD技术可以削弱大部分噪声,有效降低原始信号的非平稳性,最后分解得到多组固有模态函数(intrinsic mode function,IMF)。
PSR最早由Packard学者等提出,该方法被广泛应用于混沌时序等问题的求解和分析[17]。通常选择坐标延迟重构法构造一维混沌时间序列x1,x2,···,xn,其中xn为第n个样本在不同延迟时间τ和嵌入维度d下的数据[18]。
支持向量机(support vector machines, SVM)是一种高效进行求解分类和回归等问题的机器学习算法[19]。其功能主要通过惩罚函数和核函数实现在数据空间内寻找异类支持向量最大间隔来划分超平面,进而得到最优的决策边界。当SVM应用于回归问题时,SVM则变为支持向量回归SVR,SVR利用支持向量分类中的最优超平面的决策边界来建立回归模型[10-15]。若第i个负荷数据集合为(xi,yi),xi为样本输入,yi为样本输出,ϕi为xi映射到高维特征空间后的特征向量,其对应的最优超平面f(xi)公式如下,详细过程见参考文献[19]。

式中: ω 为法向量;b为位移项。
本文依据多阶段优化理论基础提出多阶段优化的变分模态分解-相空间重构-粒子群结合支持向量机回归(variational mode decomposition phase space reconstruction particle swarm optimization support vector regression, VMD-PSR-PSO-SVR)的短期负荷预测模型。
2 短期负荷多阶段优化预测模型
本文采用PSO算法优选SVR模型的惩罚系数C和核函数g,并建立起粒子群算法优化支持向量回归(particle swarm optimization support vector regression, PSO-SVR)预测模型,提升模型的预测性能。PSO作为一种群智能优化算法,通过粒子状态初始化,并在之后的寻优和迭代过程中不断比较个体最优和全局最优来动态调整粒子对环境的适应度,搜寻可以将粒子群中的个体移动到最优区域的解[20]。相较于GA算法,PSO减少了交叉、变异等操作,结构简易且收敛较快。同时,本文在PSO算法寻优迭代过程中加入交叉验证,以减小模型预测过程中出现的过拟合情况,并提升模型预测的准确性。
基于VMD-PSR-PSO-SVR的短期电力负荷预测模型具体流程如图1所示。首先基于VMD预处理原始负荷序列,分解获得不同频率尺度的多个平稳性的模态分量。接着PSR优化重组序列,建立多组SVR预测模型。采用PSO算法优化SVR的参数,形成PSO-SVR模型。最后累加所有分量的预测值,获得最终预测结果,并通过对比分析验证所提模型的有效性。

图1 多阶段优化预测模型流程Fig. 1 Multi-stage optimization prediction model process
为定量评估各模型的预测性能,提出平均绝对误差(mean absolute error,MAE)、均方根误差(root mean square error,RMSE)、平均绝对百分比误差(mean absolute percentage error,MAPE)和拟合优度检验(r-squared,R2)等评价指标。同时,为研究和分析各模型预测误差的分布特性,对各模型的预测误差进行统计分析和高斯混合分布检验[21-22]。
假设模型的预测误差序列服从特定概率分布,则满足一定预测误差的高斯分布公式为
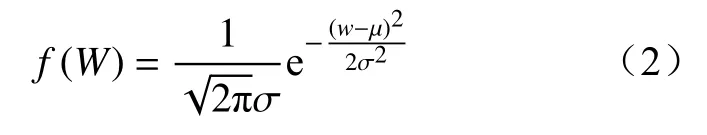
式中:µ、σ分别为误差值的期望值和标准差;W为预测误差;f(W)为预测误差序列。
3 实例计算应用
本文选取2018年8月21日—2018年8月27日某市实测到的负荷值。其中,采样频率为15 min/次,共包含672个负荷值。将前6天的数据用于训练模型,第7天的96个数据用于检验。模型相关参数设置如表1所示。

表1 模型的参数设置Table 1 Model parameter settings
模态分解技术可有效虚弱削弱序列的非线性。本文采用分解效率较高的VMD技术进行分解,实现对负荷序列的预处理。然而其模态分解个数M对分解效果影响较大,经过试验,M值取4时最合适。当M取5时,新增模态分量的中心频率与M为4时分量的中心频率较为接近,频率分布对比如图2所示。在图2中,IMF1—IMF5表示各个模态分量名称。

图2 不同模态个数下的中心频率Fig. 2 The central frequency under different modes
为避免“模态混叠”情况[22],VMD的参数M、 γ、 α应分别取值为4、0、2 000,从而得到不同频率尺度下4个具有平稳性的模态分量,如图3所示。

图3 VMD处理获得的模态分量Fig. 3 Mode obtained by VMD process components
传统“分解-预测-重构”的模式会直接把分解后的模态输送到预测模型。考虑到短期电力负荷序列具有混沌时序特性,第2阶段优化将对分解后的分量序列采用PSR进一步的优化和重组。当参数延迟时间 τ取1,嵌入维度d取5时,所得优化后的序列能够模拟实际负荷的波动情况,使得预测模型更好地进行训练和预测。
第3阶段采用SVR模型对所得优化后的分量序列进行训练和预测。由于SVR模型受内部的超参数影响较大,故采用PSO优化算法对SVR模型关键的惩罚系数C和核参数g进行寻优。其中粒子群的种群规模不宜过大,此处设置为30。最大的迭代次数设置为100。加速常数c1和c2的取值均为1.5。惩罚系数C和核参数g的搜索范围在[2-10,210]范围内。
综上,本文提出了多阶段优化策略,首先采用VMD和PSR对原始电力负荷序列进行预处理,优化序列分量。其次利用PSO算法优化SVR模型的参数,进而建立PSO-SVR优化模型。再次对数据进行归一化、训练和预测过程,得到4组序列分量的预测值。最后将预测值进行反归一化并累加求和,完成最终的短期电力负荷预测。具体的预测误差评价指标如表2所示。从表2可知,本文提出的模型得到各序列分量的预测误差值较小,且“重构”后的负荷序列可以很好地拟合测试集上的负荷数据点,有着较为满意的预测效果。
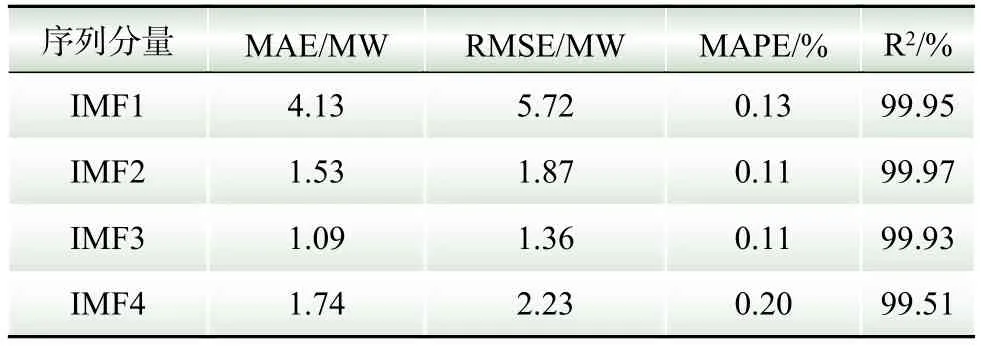
表2 各序列分量的预测误差Table 2 The prediction error of each sequence component
4 各模型对比分析
将传统BP、SVR、PSO-SVR模型和经验模态分解结合支持向量机回归(empirical mode decomposition support vector regression, EMDSVR)、集成经验模态分解结合支持向量机回归(ensemble empirical mode decomposition support vector regression, EEMD-SVR)、变分模态分解结合支持向量机回归(variational mode decomposition support vector regression, VMD-SVR)以及VMD与遗传算法优化SVR(variational mode decomposition genetic algorithm support vector regression, VMD-GASVR)等模型选取合适的参数进行多次试验,得到较佳的预测结果,并将其与本文提出的模型进行对比,得到各模型预测误差的评价指标值,如表3所示。由表3可知,本文所提出的多阶段优化模型取得了最高的预测精度,预测误差最小。其中,MAE、RMSE、MAPE和R2等指标值分别为34.76 MW、43.01 MW、1.03%和98.93%。对比SVR模型,模型的预测性能有很大提升,同样优于未采用PSO算法优化的VMD-SVR模型。
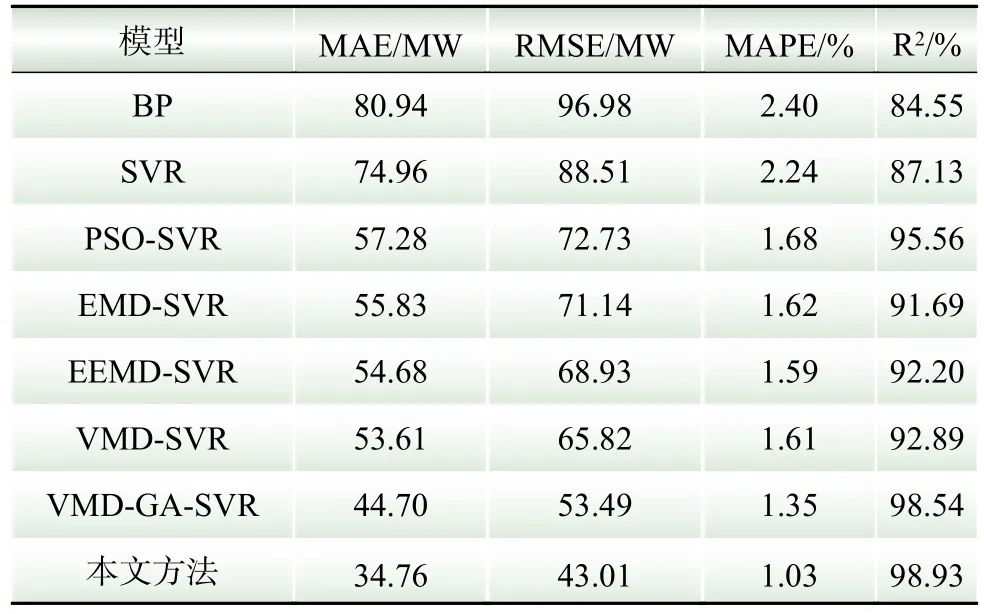
表3 各模型的预测结果对比Table 3 Comparison of prediction results of each model
2类对比模型和本文模型在测试集上的预测效果如图4所示。由图4可知,本文提出的模型相对传统模型和模态分解的模型,可以更好地拟合未来短期负荷序列,具有较好的适应性。
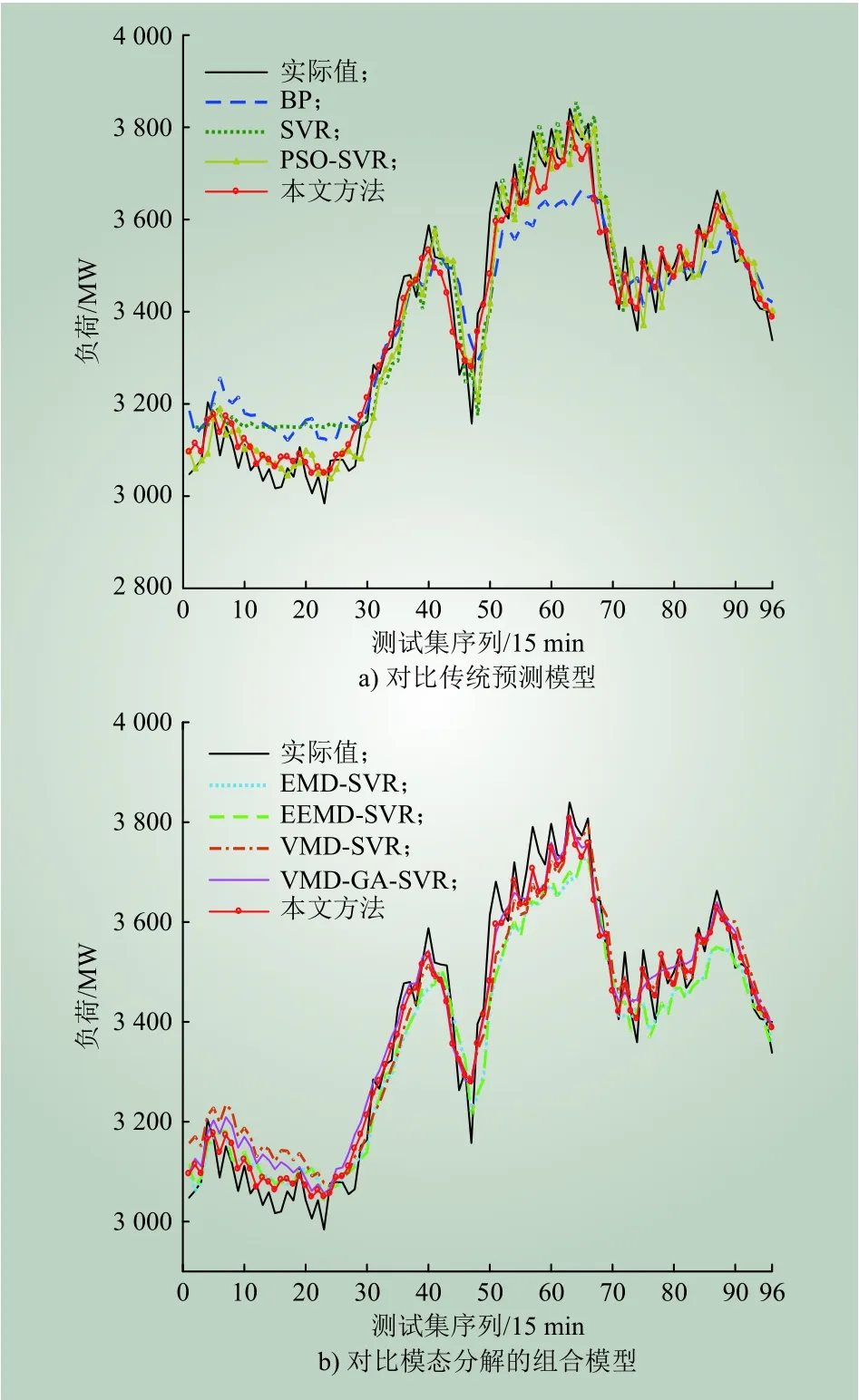
图4 不同模型的预测效果对比Fig. 4 Comparison of prediction effects of different models
结合表3和图4可以看出,SVR模型较BP模型求解效率更高、更稳定。PSO-SVR模型对比BP和SVR模型有较大的提升,甚至超过VMD-SVR模型,显著改善SVR模型的预测性能,体现了PSO参数寻优的有效性。PSO-SVR模型较SVR模型降低了误差,但对比其他组合预测模型仍有差距,这表明直接利用PSO算法优化SVR模型的能力有限,易出现过拟合情况。
另外,利用模态分技术中VMD-SVR模型要优于EMD-SVR、EEMD-SVR模型,也优于传统的BP和SVR模型,这表明了模态分解技术可以削弱负荷序列的非平稳性,降低预测难度和改善传统模型预测性能的实用性,同时反映出VMD分解的高效性能。对比实验中采用GA算法的VMD-GA-SVR模型也取得了较好的预测效果,其中拟合优度检验值R2达到98.54%,与本文采用PSO算法寻优所得的最优解仅相差0.39%,这说明两者算法在效果上接近,但本文模型在求解效率和预测精度上更具有优势。
为进一步深入分析各模型的预测误差分布情况,评价各模型的观测精度,采用高斯分布拟合检验对其进行分析,分别计算其均值、标准差和方差等指标[21-26],得到误差分布,如图5所示。由图5可知,本文所提多阶段优化的混合预测模型在测试集上的预测误差分布于零点附近,即误差较小的区间概率密度较大,观测精度较高。而BP、SVR等模型误差分布的范围较广,在误差较大处的概率密度也较高。同时,所提模型的观测精度也优于VMD-GA-SVR等优化模型。这表明与其他模型相比,本文模型可以较好地拟合整个测试集上的实际预测点位,更适合于短期电力负荷的准确预测。
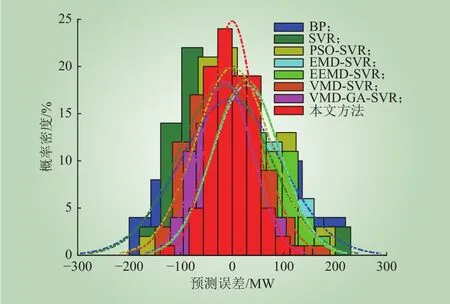
图5 预测误差分布情况Fig. 5 Distribution of prediction error
5 结论
本文基于多阶段优化的VMD-PSR-PSO-SVR模型开展短期电力负荷的预测,并与传统BP、SVR模型和采用模态分解处理的EMD-SVR、EEMDSVR、VMD-SVR和VMD-GA-SVR模型进行对比分析,得出以下结论。
(1)本文模型采用VMD预处理负荷序列,分解效率优于EMD和EEMD,充分削弱了原始序列的非平稳性,降低了预测难度,提升了预测精度。
(2)采用PSR优化模态分量序列和SVR模型的训练和拟合,可以更好地实现对历史负荷数据的学习和对未来负荷序列的预测。
(3)为克服传统SVR模型的求解效率不高的缺点,经过PSO算法优化SVR的内部参数,提出PSO-SVR模型,增强了本文模型的预测性能。
(4)本文模型将历史数据预处理、预测模型优化以及预测误差分析相结合,开展短期负荷预测的研究,有利于取得较高的预测精度。
