基于有限元分析的油库储油罐软土地基不均匀下沉数值模拟

李 博，孟蔓菁，邵文婷

（上海市建筑科学研究院有限公司，上海市 201108）

0 引 言

能源为人们生活提供动力来源，稳定的能源供给对国家、社会安全稳定发展具有重要意义。近年来，我国综合实力稳步提升，能源需求随之不断提高，促进了石油化工行业的迅速发展。随着原油、石油储运工作的日益完善，储油罐安全问题受到极大重视[1]。储油罐内存储着大量易燃易爆液体，若地基处理不当，在储油罐受到震动破坏的情况下，可能造成储油罐地基开裂等[2]，使油罐内大量液体泄漏，从而威胁人民生命财产安全。储油罐结构特殊，地基压力、油罐直径和受力面积大，外荷载复杂，而储油罐放置的软土地基具有明显的流变特性，压缩性高[3]。油库建立于软弱地基上将使地基不均匀沉降，存在众多隐患。当油库储油罐的软土地基出现不均匀沉降时，罐内液面倾斜，罐体四周沉降差明显，将造成焊缝破坏以及底板拉裂问题，油品若泄漏则危害性巨大。为此，相关研究者进行了大量研究。

陈建峰等[4]提出软土地基刚/ 柔性组合墙面加筋土挡墙离散连续耦合数值模拟方法。该方法构建离散- 连续耦合数值模型，通过PFC 和FLAC 程序对处理后的软土地基进行分析，获取其组合后软土地基的内部性状以及外部稳定性，对挡墙沉降、位移量以及弯矩的变化进行数值模拟，获取软土地基最大的荷载力。该方法对软土地基数值模拟的准确度较高，对软土地基的改进具有一定助益，但该方法在获取软土地基相关下沉值时，对其不均匀性考虑甚少。宋晶等[5]提出对结构性软土路基沉降数值进行模拟。该方法构建软土本构模型，分析现有路基软土固结情况，在此基础上，对其施工过程进行反推，获取施工前原状土的基本参数值，通过水-土耦合有限元程序对软土地基进行沉降分析。该方法通过对土层结构性、渗透性，软土层厚度进行有效模拟，可以确定软土地基设置的基础值。但该方法模拟的过程较为复杂，模拟耗时较长，工作效率较低。

基于上述模拟方法中存在的问题，本文采用有限元分析软件来模拟油库立式储油罐软土地基不均匀下沉数值。将ANSYS 软件应用于油库储油罐的软土地基不均匀下沉数值模拟中，该软件可充分模拟储油罐与地基间的相互作用以及储油罐与罐内液体的耦合情况，获取储油罐、液体和地基的数值模型，通过所建立模型实现软土地基不均匀下沉数值模拟。仿真结果表明：采用所提方法来模拟油库储油罐软土地基不均匀下沉量的效果较好，可以为油库储油罐安全运行提供理论依据。

1 油库储油罐软土地基不均匀下沉分析

1.1 油库储油罐软土地基固结沉降分析

在软土地基沉降力学中，固结沉降指在饱和土中增加荷载，土体受到压缩排除水分，土内孔隙水压力转化为应力，土粒受到应力，导致其变形渐稳的地质现象[6-7]。随着荷载的逐渐增加，土体内孔隙水渐渐流失，土层体积逐渐缩小，导致地表出现沉降。土的孔隙率由于地层体积的减小导致其渗透性下降。因此，对地基沉降的固结分析极为必要[8-9]。

在油库储油罐软土地基不均匀沉降模拟中，由孔隙水、土粒和气体组成天然土体，土体的孔隙率和孔隙比可体现土体的松密程度，土体内孔隙体积越大，孔隙率和孔隙比越大，土体的松散程度越高。土体受到固结沉降影响时，由于固结作用所造成的压密变形逐渐变大。由于土体孔隙内水不断减少，导致地基软土土体的孔隙体积不断缩小，在压力作用下，土体呈现压缩状态。有效应力的变大，令孔隙水压力降低，是导致软土地基固结的实质，土内孔压是土体固结的主要影响因素。软土地基沉降的理论计算公式为：

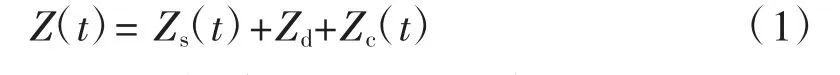
式中：Z（t）和Zs（t）分别为地层在固定时间t 下的总沉降量和次固结沉降量；Zd和Zc（t）分别为地层的瞬时总沉降量和地层排水的主固结沉降量。

软土中超静水压力消失引起的沉降为次固结沉降，而次固结沉降量通常较小[10-11]，可忽略不计。

利用主固结沉降量Zc和沉降系数m 获取的最终瞬时沉降量为C∞：

式中：m 为综合考虑因剪切变形造成的附加沉降和荷载条件等其他因素的经验系数，通常m 值为[1.1～1.7]。

通常地层的瞬时总沉降量为：

式中：P 与F 分别为油库底面中点的最大垂直荷载和中线沉降系数；E 与B 分别为通过无侧限抗压试验所获取的弹性模量平均值和荷载有效宽度。

增加荷载情况下的瞬时沉降量为：

式中：Z'd和Pt分别为时间为t 时累计荷载的瞬时沉降量和累积荷载；∑ΔP 表示所获取的累积总荷载。

在油库储油罐软土地基基坑开挖前的降水，将造成油库周围地层的土体压缩并形成主固结沉降[12]，其主固结沉降量为：

式中：Zc∞和分别为地层的最终固结沉降量和地层的平均固结度。

油库储油罐软土地基沉降包括地层最终固结沉降量和土体固结度的计算。油库储油罐软土地基沉降的平均固结度为：

依据一维固结理论可知，软土地基的平均孔隙水压力等同于地基平均固结度[13]，可依据应力得到油库储油罐软土地基平均固结度为：

在上述分析中，可根据油库储油罐软土地基由孔隙水、土粒和气体组成的天然土体孔隙率，分析油库储油罐软土地基固结沉降的影响因素，获取油库储油罐软土地基沉降的平均固结度。

1.2 非线性有限元分析

在上述获取的油库储油罐软土地基沉降的平均固结度基础上，采用有限元分析方法对油库储油罐软土地基固结沉降进行分析。有限元分析方法可分析结构变形和材料的非线性问题。油库储油罐软土地基的不均匀下沉属于材料非线性问题。软土地基的应力- 应变关系为曲线状态时表明其为非线性状态，采用有限元分析油库储油罐软土地基不均匀下沉情况时，分析单元符合几何条件[14]，其物理关系符合虎克定律。

将材料的非线性状态引入到油库储油罐软土地基中，分析油库储油罐软土地基固结沉降的非线性特征。假设弹性矩阵S、劲度矩阵K 随应变和应力发生改变，而非常量，劲度矩阵随结点位移发生变化，此时模拟结构的平衡方程组公式为：

式中：K（δ）和δ 分别为劲度矩阵和结点位移；R 表示点荷载列阵。式（8）由结点位移的线性方程组转化为非线性方程组[15-16]，采用初应力（变）迭代法对非线性方程组求解。

假设σ0与ε0分别表示结构中所存在的初应力和初应变，可得应力σ-应变ε 公式为：

式（9）可转化为：

应力- 应变间的非线性关系可通过初应力σ0的变化体现，通过初应力法实现应力- 应变间关系的非线性解答[4，17]，可得非线性应力- 应变关系的初应变法，其解为：

当应力-应变曲线呈现σ = f（ε）的显性关系时，选取初应力法；当应力- 应变曲线呈现ε = f（σ）关系时，采用初应变法。

根据有限元分析方法和虎克定律，分析油库储油罐软土地基的非线性特征，确定不同状况下应力的选择。

1.3 油库储油罐软土地基模型构建

在上述分析基础上，采用ANSYS 软件构建油库储油罐软土地基模型。该软件是一款大型通用的有限元分析软件，能与多数CAD 软件接口，实现数据的共享和交换，主要用于分析不同性质的岩土材料在固定强度极限时造成的塑性流动和破坏现象的力学行为的数值模拟。ANSYS 软件同样可应用于大形变状态下的失稳状态和破坏状态，可有效分析基础力学问题和岩土工程问题。图1 为有限元分析软件模拟的立式储油罐模型，图2 为油库储油罐软土地基不均匀下沉的数值模型。

图1 立式储油罐模型（单位：P a）

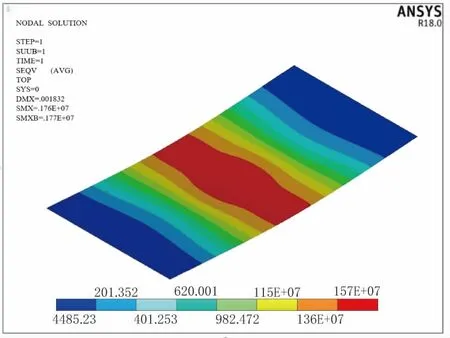
图2 油库储油罐软土地基的不均匀下沉数值模型（单位：P a）

采用开尔文体和麦克斯维尔体串联的伯格体模型建立油库储油罐软土地基模型。伯格体力学模型见图3；柏格体蠕变曲线见图4。

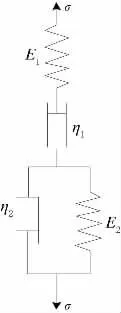
图3 柏格体力学模型

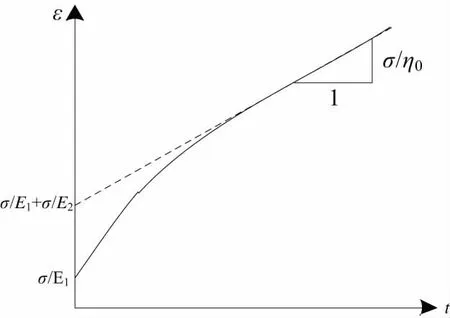
图4 柏格体蠕变曲线

通过柏格体蠕变曲线，可体现油库储油罐软土地基不均匀下沉情况，其蠕变方程为：

式中：η1为初始蠕变阶段抗剪强度；η2为稳定蠕变阶段抗剪强度；E1是初始蠕变阶段塑性流动值；E2是稳定蠕变阶段塑性流动值。

当应力σ 为常量状态时，可得应变为：

对于油库储油罐软土地基内随意点，随机平面上的剪应力与软土地基抗剪强度相同时为极限平衡状态[18-19]。极限平衡状态下油库储油罐软土地基随机点的最大主应力与最小主应力之间的关系为：

式中：σ1为最大主应力；σ3为最小主应力；δ 和c 分别为土体内摩擦角和土体黏聚力。

在油库储油罐软土地基不均匀沉降数值模拟过程中，逐次迭代土体应力，利用迭代结果判断油库储油罐软土地基是否出现剪切破坏情况。该模型可体现软土地基的复杂特性，并且体现软土地基的弹性、黏性、塑性及软土地基受到的剪切破坏。结合油库储油罐软土地基工程性质，建立油库储油罐软土地基模型。

2 仿真分析

2.1 仿真环境及参数

选取某大型油库作为数值模拟分析对象，油库内包含2 个体积为11 657.25 m3的储油罐，依据储油罐布置要求，将油罐单排布置。储油罐内径和高度分别为30 m 和16.5 m，储油罐间距为18 m。油罐钢板厚度为5 mm，自重约59 158 kg。对储油罐充水预压，将高度为16 m 的水视为1.6×105Pa 的均布荷载；将高度为16 m 的油品视为1.3×105Pa 的均布荷载。为降低由于边界条件引起的数值模拟误差，设置大量土体延伸于储油罐四周，软土延伸长度和软土层厚度分别设置为55 m 和32 m；在储油罐下部设置硬质材料的护坡式基础，设置沥青砂绝缘层和砂垫层，素土夯实，原土整平，用沥青封口，采用厚20 mm 的1∶2 水泥砂浆，毛石护坡M2.5，护坡基础面积约2 500 m2。

油库储油罐各层软土地基的物理性能见表1。

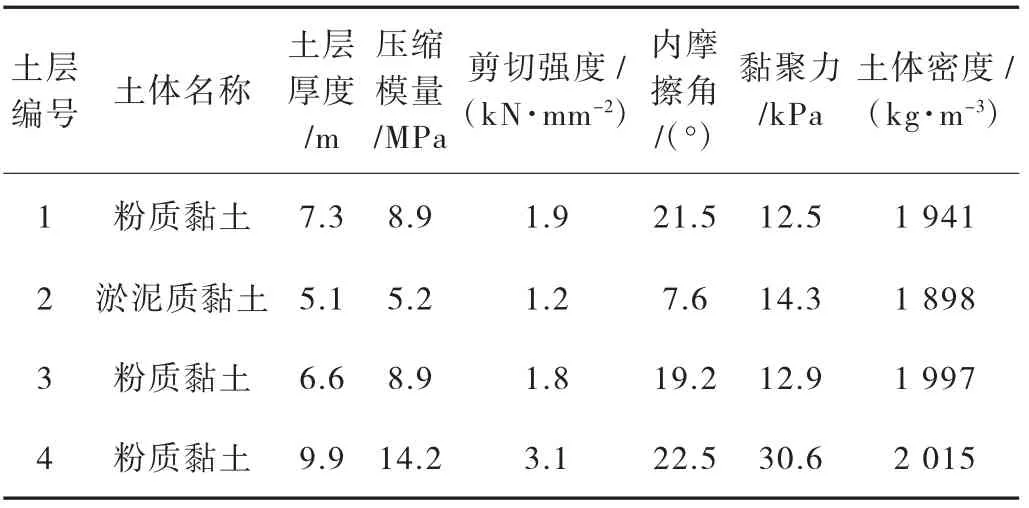
表1 软土物理性能

2.2 仿真结果分析

为模拟储油罐软土地基的不均匀沉降情况，将分级加载方式应用于ANSYS 仿真软件中，设置所建立模型的底面与侧面的法向位移约束均为0。设置充水预压荷载，采用1 次、4 次和8 次的加载方式进行仿真试验。1 次充水加载液位值为300 mm，应力值为235.25 MPa；4 次充水加载液位值分别为100 mm、200 mm、300 mm 和400 mm，应力值分别为68.35MPa、155.36 MPa、235.25 MPa 和345.25 MPa；8 次充水加载液位值的前4 次液位值和应力值与4 次充水加载时相同，后4 次液位值分别为500 mm、600 mm、700 mm和800 mm，应力值则分别为418.16 MPa、475.26 MPa、552.14 MPa 和621.62 MPa。每次注水后需静止1 h，使试验数据稳定。所获取的储油罐底板软土地基沉降曲线见图5。

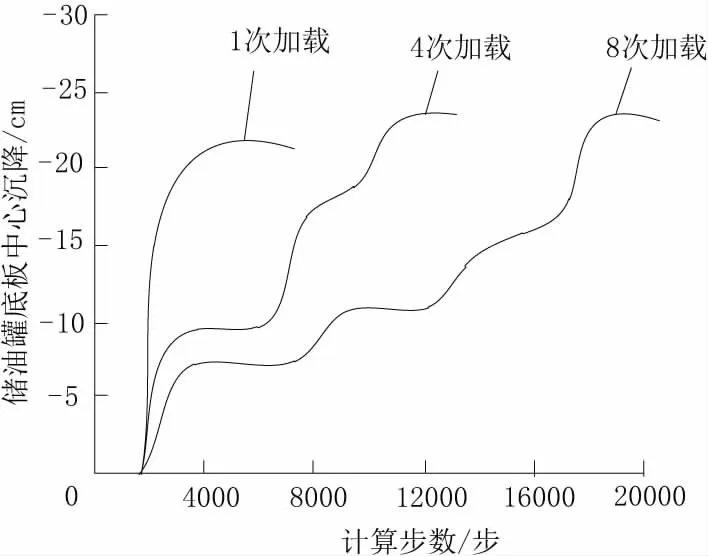
图5 不同加载方式下储油罐沉降曲线变化

由图5 可知，通过1 次、4 次和8 次加载，储油罐底板中心沉降量最大值分别为20.58 cm、22.35 cm和22.35 cm，所需计算步数分别为5 864、12 248 和21 886 次。综合分析图5 数值模拟精度和数值模拟所需计算时间，采用4 次加载方式，作为油库储油罐软土地基不均匀下沉数值模拟的加载方式。

利用荷载和模型对称性，获取油库储油罐单排双罐的模拟结果和同步充水的双罐简化图，见图6。

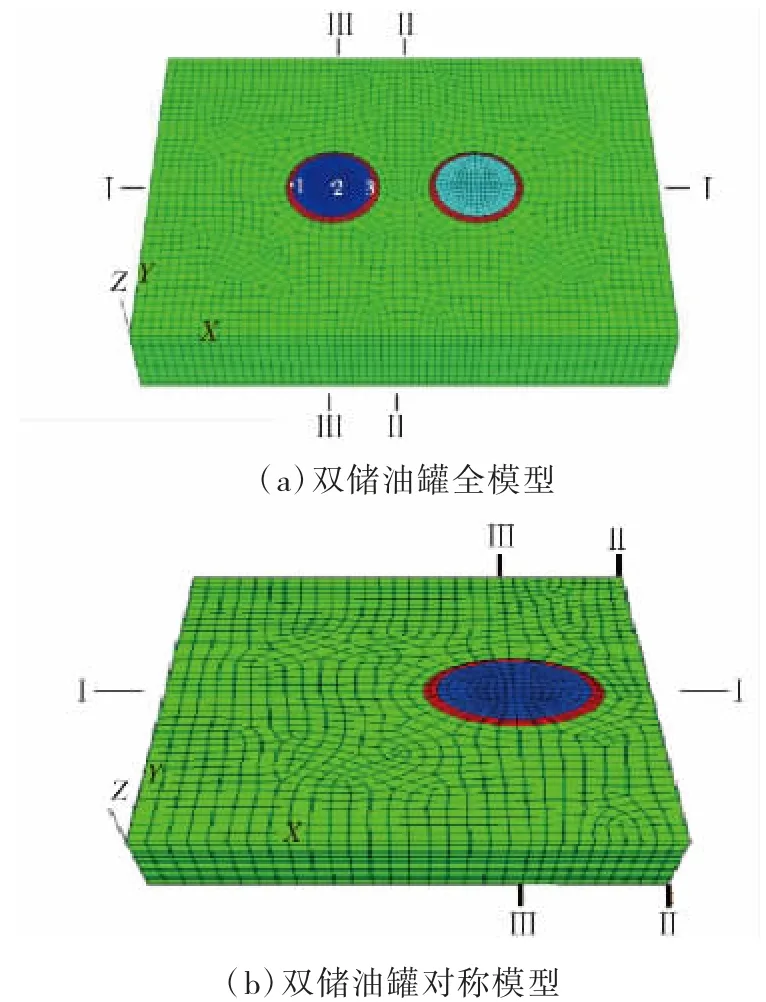
图6 油库储油罐单双罐模拟图

由图6 可知，采用本文方法可以有效建立油库储油罐软土地基不均匀下沉模型，具有较高的数值模拟有效性。图6（a）中点2 为储油罐底板中心，点1和点3 分别对应X 方向的底板直径断点。监测以上部位沉降，获取储油罐底板中心点2 的沉降曲线及点1 与点3 间的沉降差，即最大不均匀沉降差。点1和点3 的罐周平均沉降曲线即储油罐整体不均匀沉降曲线，见图7。

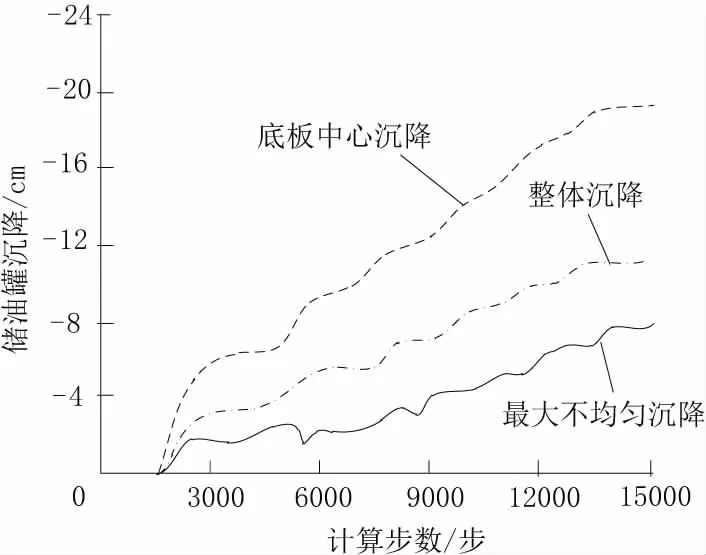
图7 储油罐整体不均匀沉降曲线

由图7 可知，2 个储油罐在同步充水情况下，沉降性状相同。储油罐底板中心沉降和整体沉降最大值分别为19.58 cm 和10.57 cm。储油罐底板中心沉降和整体沉降在施加荷载时逐步提升。软土地基内由储油罐底板压力形成从底板中心至径向及深度方向逐渐降低并扩散的附加应力。

图6（a）中右侧储油罐在下侧地基所形成的附加应力逐渐降低，其中点3 处左罐罐周所形成的沉降最高，并逐渐向点1 部分降低；储油罐从点1 至点3逐渐倾斜，2 个储油罐逐渐倾斜至互相方向。罐中与罐周存在过大的沉降差，将造成底板钢材附加应力过大。在储油罐制作过程中可将底板设置起拱，从而提升储油罐存储安全性。

图6（a）中各轴线的地基表面各点沉降曲线模拟结果见图8。

图8 各轴软土地基表面沉降曲线分析

由图8 可知，Ⅰ轴线的地基表面沉降曲线在双罐同步加载情况下，以“勺形”呈现，与罐中心两侧长度相同的点沉降量相比有所降低，但与原点一侧较远离部位的沉降量相比较高。Ⅱ轴和Ⅲ轴呈现单抛物线型地基表面沉降，以Ⅰ轴为中心，这2 个轴线上的地基表面沉降量在对称轴上最大，与对称轴距离较远时沉降量有所降低。Ⅲ轴线的隆起程度比Ⅱ轴线低，验证了双罐压力对Ⅱ轴线两侧的影响力高于Ⅲ轴，且Ⅰ轴线两侧隆起位移低于Ⅱ轴线与Ⅲ轴线两端地基表面的隆起位移。

油库内2 个储油罐中心点沉降量对比曲线见图9。

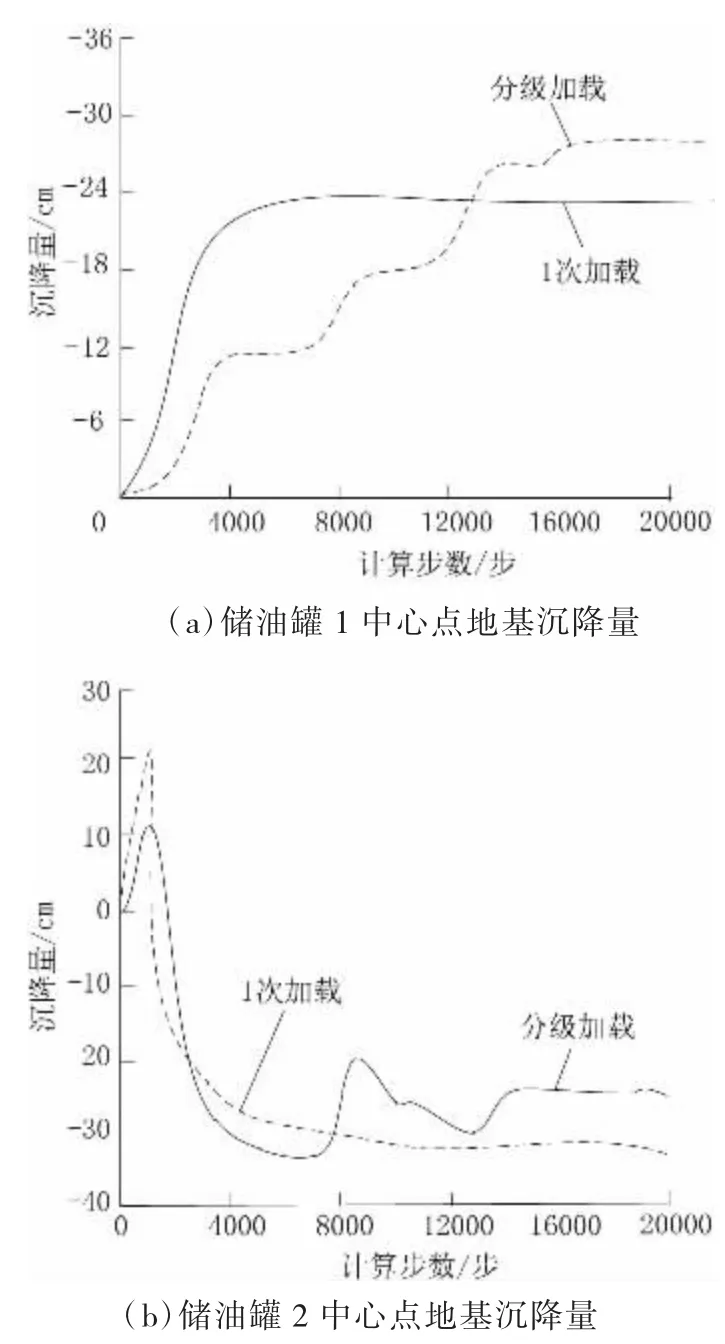
图9 储油罐中心点沉降量对比

由图9 可知，储油罐1 的中心点在不同加载方式下具有较大的变化。1 次加载方式下，软土地基受到超孔隙水压力作用，中心点沉降量较小；分级加载方式下，软土地基基本未受到超孔隙水压力作用，软土地基最终沉降量明显大于1 次加载方式下的沉降量。由此说明，当加载方式存在变化时，储油罐受到相邻储油罐影响，中心点沉降量有所变化。

分级加载方式下，初始加载时储油罐中心点隆起和完成加载时的沉降量均低于1 次加载方式下的相应值。在地基土的外力作用下，初始加载造成的超孔隙水压力明显超过地基附加应力，1 次加载方式下的外力作用大于分级加载方式下的外力作用，因此，分级加载方式所造成的隆起较小。1 次加载方式下，软土出现塑性变形现象，导致其沉降提升；分级加载方式下，软土出现弹性变形情况，软土结构在下一级加载时逐渐密实，承载力有所提升，沉降量较小，不均匀下沉量低于1 次加载方式。

3 结 语

本文基于ANSYS 软件对储油罐软土地基不均匀下沉进行数值模拟，分析储油罐软土地基在1 次加载和分级加载方式下的不均匀下沉现象。分析了油库储油罐软土地基固结沉降的影响因素和平均固结度；根据有限元分析方法和虎克定律，分析了油库储油罐软土地基的非线性特征，确定了油库储油罐软土地基在不同状况下的应力；采用仿真试验验证了数值模拟油库储油罐软土地基不均匀下沉的有效性。