地铁对高压天然气管道杂散电流干扰监测评价

1 概述

随着城市建设发展，地铁附近天然气管道遭受干扰的报道日益增多。北京地铁第一期工程投入运营数年后，其主体结构钢筋发现严重腐蚀，隧道内水管腐蚀穿孔，仅东段部分区段更换穿孔水管54处

。上海地铁二号线世纪大道DN 300 mm天然气钢管已发生近10次腐蚀泄漏事故，直接或间接损失高达200×10

元

。1999年广州地铁一号线全线开通，2000年起，市区中压管网腐蚀抢修数量大幅上升，并一直处于高位状态

。王红霞等分析了某机坪输油管道保护电位出现的严重漂移现象，发现其电位漂移时间与通往该机场的地铁开始调试和正式运行的时间吻合，确定该干扰来源于地铁直流杂散电流

。

通过现场诊断有效防护、进而消除杂散电流对钢质管道的干扰，是近年来的研究热点。赵晋云等通过测试新大线输油管道管地电位等参数，明确了干扰来自与管道近距离平行的大连快轨三号线，并提出增加阴极保护装置和极性接地排流来抑制杂散电流干扰

。刘军使用一种新型的极化试片电流测试方法，采用高精度数据记录仪，直接监测受到动态杂散电流干扰的极化试片中流进、流出的直流电流，对其评价，进而为查找直流杂散电流干扰腐蚀风险点提供依据

。蔡彬彬等分析南京地铁二号线马群车辆段杂散电流腐蚀燃气管道情况，提出了用晶闸管取代二极管的新方案，并通过治理前后数据对比，验证了其方案的可行性

。

本文对佛山新近开通的地铁二号线附近的高压天然气管道，安装无线远传监测装置，连续记录地铁开通数月内的通电电位、断电电位、牺牲阳极电流等数据，并对这些数据进行分析，以期了解地铁直流杂散电流的干扰规律，为可能采取的防治措施提供依据。根据动态杂散电流评价标准，确定管道的腐蚀风险等级，并提出了阴极保护系统改进建议。

2 测试现场概况

现场测点布置见图1。出南庄门站的天然气管道(红色)向北延伸到季华西路后折向西，另一路直接向北延伸。地铁正线位于季华西路中央下方12～15 m深处，在以地铁车库为中心、半径2 km左右的管道上，选取9个测点。1号测点位于湖涌站西偏南805 m，2号测点位于湖涌站南侧119 m，地铁自1号测点、2号测点之间穿过。3号测点位于地铁正线南侧110 m，距湖涌站630 m。4号测点是出南庄门站管道南行的首个测试桩， 5号测点位于南庄门站东侧。6号测点和7号测点西侧为地铁车库，紧邻进出库轨道。在更北侧的管道上，选择8号和9号测点，观察受地铁干扰的情况。

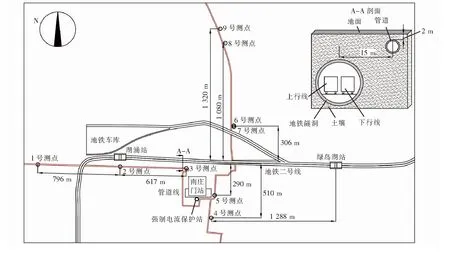
测试区域内天然气管道以5号测点为界，北侧和南侧管道2006年投产，西侧管道2013年投产，全部采用加强级3PE防腐层。管道防腐层状况整体良好，总长度约4 860 m管段中，仅204 m管段分级评价为3～4级，3级评价为“老化程度及表现处于老化较轻，基本完整”，4级评价为“老化较严重、有剥离和较严重的吸水现象”。该区域内的管道阴极保护采用强制电流结合局部牺牲阳极的方式。南庄门站内设强制电流保护站，设定为恒电流输出模式。除4号测点(无牺牲阳极)外，1号、2号、3号、5号、7号、8号、9号测点均布设镁阳极，6 号测点布设锌阳极。

3 测试设备功能

9个测点上安装自行开发的杂散电流无线远传监测装置，见图2。测量参数包括：通电电位、断电电位、牺牲阳极电流、交流干扰电压。具有本地存储及无线远传功能，采样频率1 Hz，24 h连续监控。使用长效铜/饱和硫酸铜(CSE)参比电极，垂直埋置在土壤中。断电电位参照GB/T 21246—2020《埋地钢质管道阴极保护参数测量方法》，采用继电器进行12 s通、3 s断连续循环，读取管道断电电位。

4 各测点电位结果与分析

4.1 通电电位、断电电位受地铁运行影响

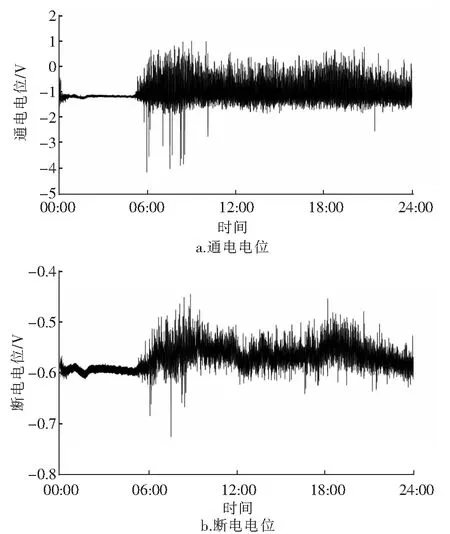
以1号测点为例，1号测点2022年3月28日通电电位、断电电位见图3。可以看出，夜间地铁停运时，通电电位、断电电位的背景值(分别称为通电背景电位、断电背景电位)基本稳定，分别为-1.17 V、-0.59 V左右。若不考虑瞬时出现的大幅负向偏移，地铁运行时段通电电位的波动范围-1.79～1.00 V，断电电位波动范围-0.625～-0.443 V。其他测点的通电电位与断电电位与1号测点相似，均受地铁运行影响严重。

4.2 电位波动与地铁运行时间关联性

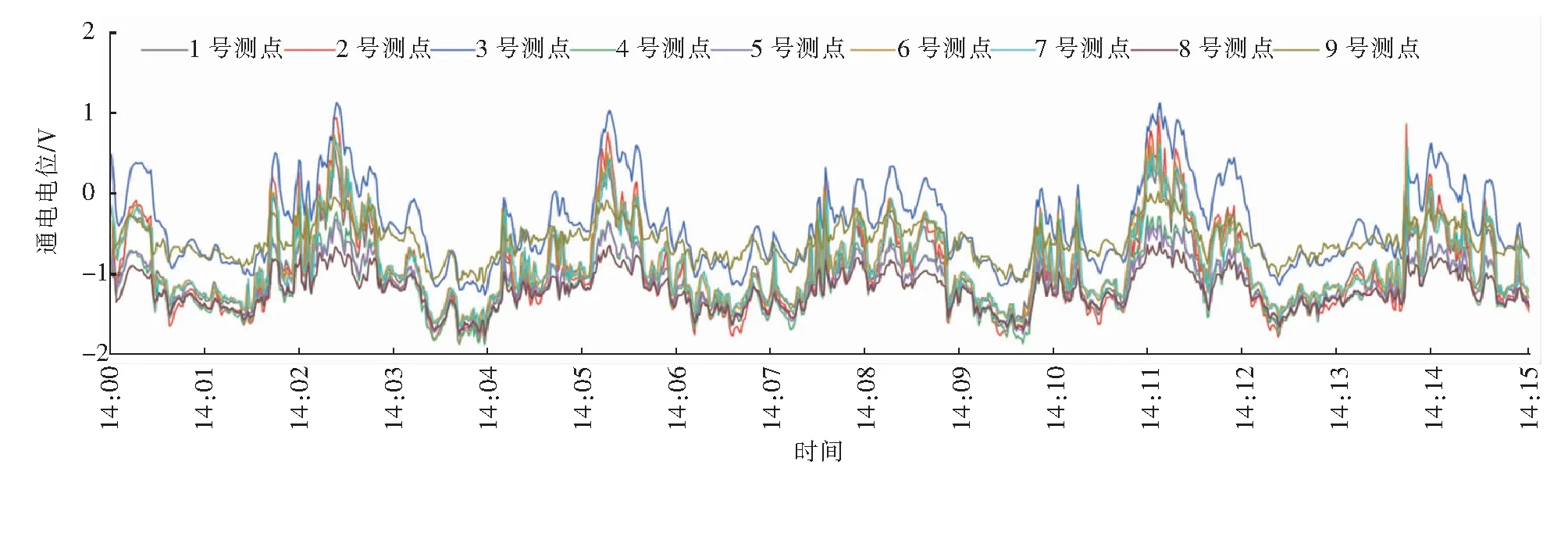
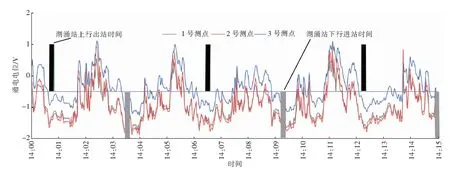
2022年1月8日14:00—14:15各测点通电电位的变化见图4。2022年1月8日14:00—14:15湖涌站地铁进出站对1～3号测点通电电位的影响见图5。

数学活动的定义非常广泛，所有的数学学习行为都是数学活动。史宁中教授将数学基本活动经验从思维上划分为观察、归纳猜想、表达、验证（证明）等几个大的维度，他认为经历了这些数学基本活动过程，积淀形成一定数学思维模式[8]，在小学数学中有数与代数、图形与几何、统计与概率、综合与应用四大领域，那么，史宁中教授的思维划分显然是，每个领域的活动都可以划分为观察、归纳猜想、表达、验证（证明）等维度。

庄子还有句话说：人能虚己以游世，其孰能害之。一个人要是不把自己当回事，那就没有人能让他愤怒，让他生气。一个人的自尊太强、自我意识太强，别人稍微冒犯，他就立马反弹回去。而每个人都有每个人的生活方式，尝试放下“我”，站在对面的角度去考虑，去理解，去宽宥。

详察古今，研精篆素，尽善尽美，其惟王逸少乎！观其点曳之工，裁成之妙，烟霏露结，状若断而还连；凤翥龙蟠，势如斜而反直。玩之不觉为倦，览之莫识其端，心慕手追，此人而已。其余区区之类，何足论哉！[9](《王羲之传》，P2108)

4.3 通、断电电位波动规律及 Pearson相关系数

① 通、断电电位波动规律分析

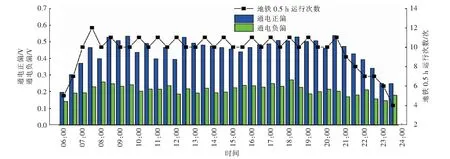
以0.5 h为统计时间间隔，对各测点通电电位相对于夜间停运时段通电背景电位的正向偏移的平均值(以下简称通电正偏)与负向偏移的平均值(以下简称通电负偏)、断电电位相对于夜间停运时段断电背景电位的正向偏移的平均值(以下简称断电正偏)与负向偏移的平均值(以下简称断电负偏)、经过各测点的地铁运行次数进行统计。以1号测点为例，2022年1月8日统计结果见图6、7，图中横坐标时间6：00对应统计时段5：30—6：00，其他时间以此类推。

图5以脉冲形式给出了地铁进出湖涌站的时刻(从东到西为下行线，从西到东为上行线)，可以看出，地铁运行的时间间隔与通电电位的波动周期完全吻合，其峰谷数量与地铁运行频次也一一对应。

② Pearson相关系数定义

采用二元变量相关分析中的Pearson相关系数

量化描述所有测点通电正偏、通电负偏、断电正偏、断电负偏与地铁0.5 h运行次数之间的相关性。

Pearson相关系数

的取值范围为[-1,1]，

>0为正相关，

<0为负相关，

=0表示不存在线性关系，|

|=1表示完全线性相关。|

|≤0.3为不存在线性相关，0.3<|

|≤0.5为低度线性相关，0.5<|

|≤0.8为显著线性相关，|

|>0.8为高度线性相关

。

③ Pearson相关系数计算结果

2022年1月8日各测点通电正偏、通电负偏、断电正偏、断电负偏与地铁0.5 h运行次数之间的Pearson相关系数见表1。

这一节中,首先给出Γ中η值平方可积函数f修正随机梯度的定义,这里“修正”是指本文的定义是在文献[8]关于随机梯度定义的基础上,考虑函数真正的“湮灭”而进行了修正,进而定义修正点态随机梯度。

高空作业，是桥梁工程施工特点重要组成部分，高空坠落事故发生率较高。施工者在高空中工作坠落、施工平台行走过程中掉落与上升时掉落，都成为了桥梁工程的安全风险。除此之外，桥梁工程施工过程中也极易发生火灾，人为原因、不合理用电、机械故障都是导致火灾发生的原因。施工现场的仓库起火爆炸、人员触电身亡的事故时有发生。这些不为人重视的风险，往往会造成巨大的损失。

4.4 电位周期与地铁运行频次的关系

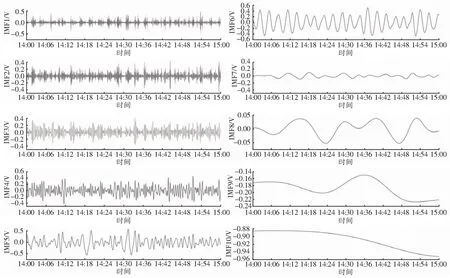
对1号测点2022年1月8日14:00—15:00通电电位进行EEMD分解，可得到频率逐渐降低的10个分量(记为IMF1～IMF10)，1号测点通电电位各分量随时间变化见图8。EEMD分解后获得的各个分量的合成值称为EEMD合成值，通电电位原始值和EEMD合成值对比见图9。

显然，测试的通断电位受到多种因素共同影响，如：地铁经过某一测点的时间间隔、某一时刻隧洞内的车辆数量和取流状况、杂散电流泄漏点数量和位置等，呈现出复杂的非线性和高度的非平稳性，直接观测原始数据信号很难判断相关影响因子的真实影响信号。EEMD算法对数据信号分解后获得的统一频谱的分量求取平均值，将对应的平均值作为对应频率的模态分量，即本征模态函数(IMF分量)。利用EEMD算法可对通断电位数据信号进行一定尺度或波动趋势的有效分解并降低信号的非平稳性，同时EEMD算法在分解信号的同时最大程度地保留了真实信号。

集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)算法，由经验模态分解(EMD)算法完善发展而来，有效避免了EMD带来的模态混叠问题

，是一种具备自适应性的信号处理方法，可将复杂的时间序列信号进行平稳化后再进行处理

，EEMD算法适用于分解非线性和非平稳性的时序波形数据信号。对各测点的通电电位使用EEMD算法，进一步分析电位的波动与地铁运行频次间的关联性。

由表1可以看出，对绝大部分测点，通电正偏、通电负偏与地铁0.5 h运行次数呈现高度线性相关和显著线性相关；除去6号测点的断电正偏与地铁0.5 h运行次数呈现高度线性相关，其余测点断电正偏呈现显著线性相关；绝大多数测点的断电负偏与地铁0.5 h运行次数呈现低度线性相关。断电负偏更多取决于管道自身的阴极保护效果，也需要针对地铁干扰进行完善。

图8中，分量IMF1、IMF2、IMF3属于高频分量，反映通电电位原始数据变化的非平稳性和非线性；分量IMF4、IMF5、IMF6反映了通电电位的周期性变化规律；分量IMF7、IMF8、IMF9一定程度反映了通电电位波动幅值变化；分量IMF10表征通电电位的平均变化趋势。

为降低随机因素的影响，Allahkaram等

对测试时段电位按从大到小进行排序，选取靠近最值的10%数据的平均值替代最大值和最小值。为使选取的最值既能减少随机因素影响，又可充分反映测试时段的断电电位波动幅值情况，本文选取靠近最值的1%数据平均值(非最大值和最小值)，以下将当日断电电位数据的最大、最小前1%数据的平均值简称断电最大1%、断电最小1%。

在2022年1月8日、9日、10日10:00—11:00，1号测点地铁运行频次与通电电位分量IMF6的对比见图10。可以看出，通过EEMD分解的信号分量中，分量IMF6变化的周期与湖涌站东西向出站的时间周期完全吻合，因而通电电位信号分解得到的分量IMF6最能反映地铁运行频次引起的杂散电流对该测点的真实影响。导致1号测点通电电位变化的因素可分为：夜间无地铁运行时段背景电位细微波动和日间地铁运行时段杂散电流泄漏两者的叠加影响。图10也说明了正是在日间地铁运行时段里地铁运行频次和多列地铁同时在轨运行时的叠加影响，直接导致了通电电位信号的周期性形态变化。

5 阴极保护状态评价

5.1 断电电位的波动性

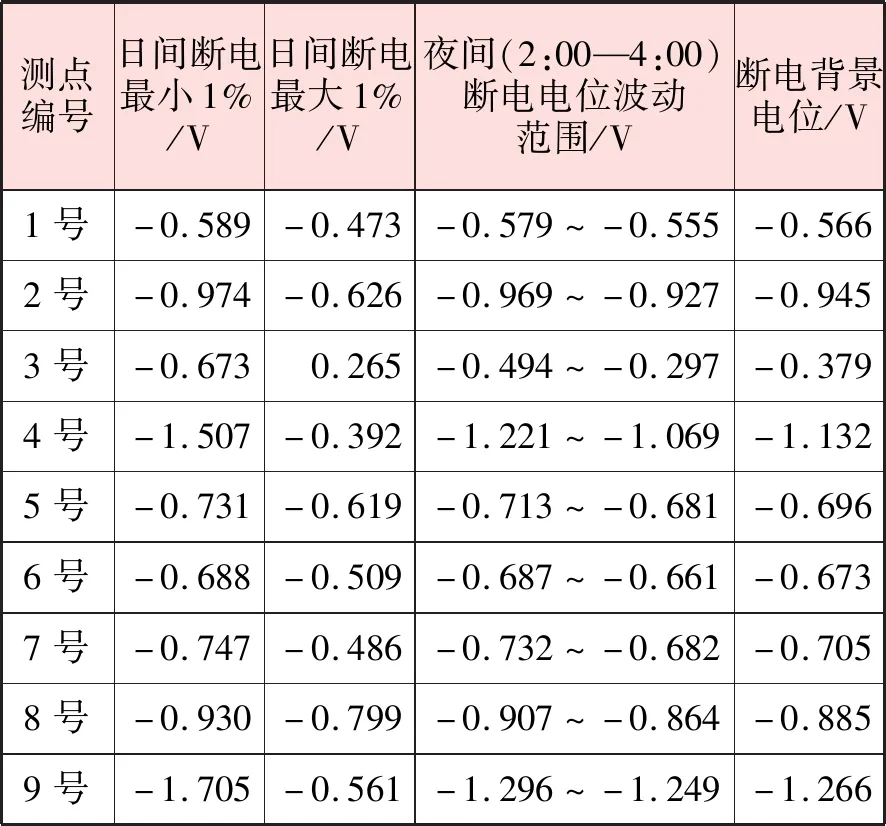
试片瞬间断电的方法可最大程度地降低土壤IR降的影响。对于泄漏的杂散电流，该方法测得的断电电位也呈现一定的波动性，但幅值比通电电位小。本文使用断电背景电位和日间波动最值评判阴极保护状态。前者为夜间停运时段断电电位的平均值，用来表征无干扰时段管道的真实阴极保护状态；后者表征断电电位1 d内上下波动幅值。

由图9可知，通电电位原始值和EEMD合成值两条曲线基本重叠，即EEMD算法分解通电电位信号时，最大程度保留了真实信号，还原度高。此外，通电电位分解后的分量时间序列曲线较为平稳和光滑，利用其中相应的分量有利于后续的通电电位波动周期性与地铁运行频次的周期性分析。

根据开关状态的不同,三相功率变换器共有8个输出电压矢量,V0(000),V1(100),V2(110),V3(010),V4(011),V5(001),V6(101),V7(111),如图2所示,三相功率变换器器输出的电压矢量可以表示为

选取若干比较典型时段，得出3号测点夜间断电电位基本在-1.124～-0.368 V，日间地铁运行时段断电电位波动范围为-2.331～+0.518 V。

由图4可以看出，杂散电流对各测点的影响几乎完全同步，只是幅值不同，其中3号、9号测点波动平均幅值分别比其他测点大0.583、0.316 V，这与两个测点距地铁线路的距离、杂散电流可能泄漏位置有关。

根据协整检验得出了能源消耗、环境污染与绿色经济增长之间存在长期稳定的均衡关系，但是无法判断三者相互影响的程度。为了弥补这个相对来说比较重要的缺陷，就需要建立误差修正模型[17]83-91。该模型不仅能够反映时间序列长期均衡关系，而且还可以得到短期偏离向长期均衡修正的机制。所以文章还需要通过Stata15软件进行误差修正模型的构建，进一步研究能源消费和环境污染当期的变化对产出当期变化的影响，即它们之间的短期波动关系。根据协整关系建立的VEC模型如下：

2022年2月24日所有测点的断电背景电位及波动范围对比见表2，日间指7：00—23：00。可以看出，较之断电背景电位，全部测点在日间的波动范围都比夜间明显增大，其中3号测点更是呈现0.265 V的正电位，腐蚀隐患很大。

设立科创板，是将资本市场进一步细分，可促进A股市场分化，主板市场上不去，海外市场又太拥挤，一些海外的中概股公司要回归国内资本市场，也没有完全对应的承接。科创板将提供一个新的资本市场入口。同时有利于克服相当一部分高科技上市公司（即俗称“独角兽”）估值偏低的弊端。实际上，高科技企业才是推动股市繁荣的根本力量。单独设立科创板，将充分肯定其客观价值，推动上市公司脱虚向实，回归资本市场的本质属性，客观反映经济，扩大直接融资，刺激科技创新，利好实体经济。

5.2 阴极保护状态评价

对于动态杂散电流干扰下施加阴极保护的管道，尚无适用的标准来评价保护状态。表3给出了澳大利亚标准AS 2832.1—2015《金属的阴极保护》(Cathodic protection of metals)中直流牵引系统对管道干扰的判定。表4给出了上海市地方标准DG/TJ 08-2302—2019 《埋地钢制燃气管道杂散电流干扰评定与防护》中杂散电流干扰风险等级评定，记相对于-850 mV断电电位正向偏移值为

。表4中，4个时段不完全匹配时，本文按前两个时段评定，因为国内外关于判断风险等级方法并无过多其他相关说明，仍具有一定的主观性。AS 2832.1—2015与DG/TJ 08-2302—2019均是按照断电电位的正向偏移时段占比进行划分，后者按照时段占比划分了高、中、低3个风险等级。

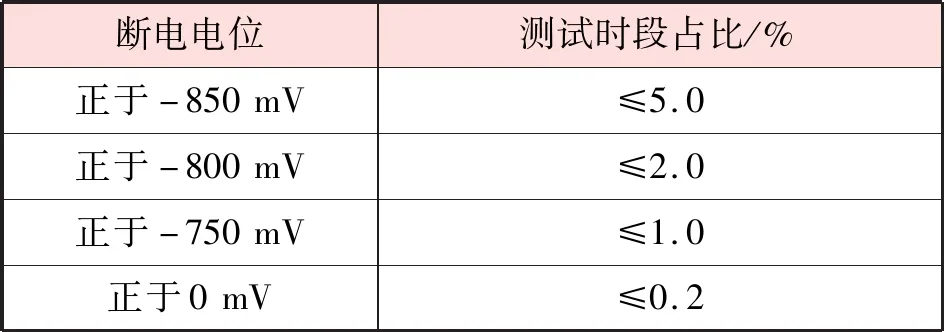
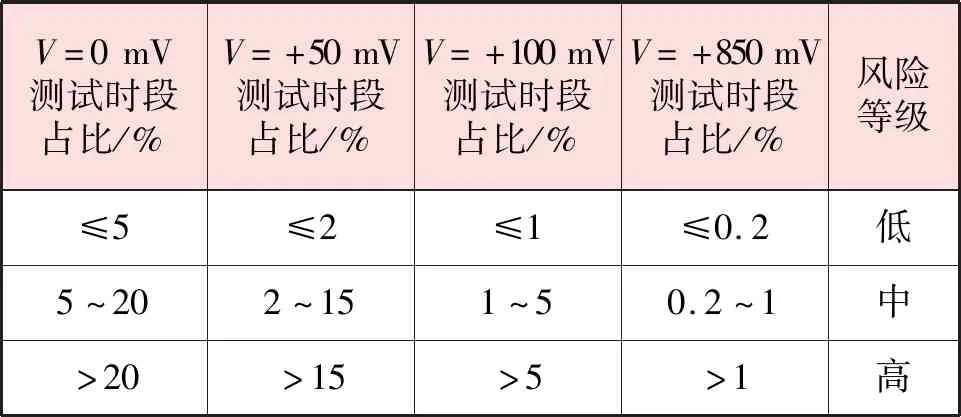
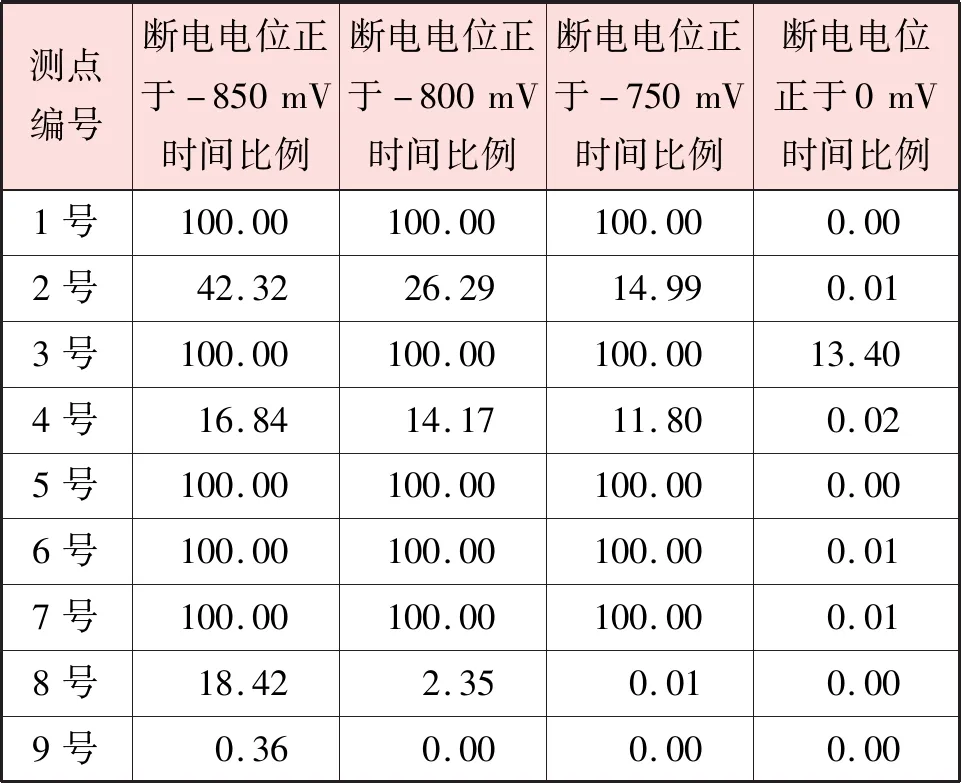
选取2022年2月24日所有测点的断电电位进行统计，结果见表5。依据DG/TJ 08-2302—2019，9号测点的干扰风险等级为低级，4号、8号测点的干扰风险等级为中级，其余测点的干扰风险等级为高级，需采取针对性防护措施，并且除2号、4号、8号、9号测点外的其他测点断电电位正向偏移十分严重，测试时段断电电位都处于正向偏移值≥100 mV的水平。

对2022年2月24日断电电位负于-1.3 V的时段占全天测试时段的比例进行统计，得出4号测点该比例达到14.69%，过负的断电电位可能会导致防腐层剥落。断电电位正、负向偏移交替作用对管道的长期影响，目前尚无系统的研究可供借鉴。

6 结论

① 管道受到地铁运行的严重干扰，日间通电电位和断电电位均大幅波动，而夜间均呈现平稳状态。通电电位的正向偏移、负向偏移以及断电电位的正向偏移，均与地铁运行频次高度或显著相关，断电电位的负向偏移与地铁运行频次的相关度较弱，更多取决于阴极保护系统自身的性能。

② 使用EEMD算法考察了通电电位，各分量的合成完整地还原了实测结果，说明EEMD算法可用于深入分析地铁所导致的通电电位波动；分量IMF6与地铁行驶周期的重叠，反映该分量可刻画地铁运行的杂散电流影响。

①根据桩的直径，在断层上方竖立一个直径适当的可折叠钢内模（内模直径大于1.5m，孔心桩壁厚应至少大于55cm）。

③ 9号测点的干扰风险等级为低级，4号、8号测点的干扰风险等级为中级，其余测点的干扰风险等级为高级，并且除2号、4号、8号、9号测点外的其他测点断电电位都处于正向偏移值≥100 mV的水平。防护措施可考虑加装极性排流器。

[1] 刘争,李威力,钟周全. 地铁杂散电流的危害及检测实例[J]. 全面腐蚀控制,2016 (9):56-58，94.

[2] 陈志光,秦朝葵,计雪松. 上海轨道交通二号线杂散电流测试分析[J]. 腐蚀与防护,2008(6):344-347.

[3] 徐颢,李代莉. 轨道交通直流杂散电流给埋地钢管防腐系统带来的新风险[J]. 城市燃气,2016(3):12-17.

[4] 王红霞,梁耀球,阮建平,等. 某机坪输油管网受地铁直流杂散电流干扰的测试与防护[J]. 全面腐蚀控制,2014(4):45-47.

[5] 赵晋云,滕延平,刘玲莉,等. 新大线管道杂散电流干扰的分析与防护[J]. 管道技术与设备,2007(2):38-40.

[6] 刘军. 动态直流杂散电流干扰中极化试片电流测量[J]. 腐蚀与防护,2016 (1):68-70，75.

[7] 蔡彬彬,刘佰川. 地铁车辆段杂散电流泄漏分析及处理[J]. 江苏科技信息,2019 (21):42-45.

[8] 张宇镭,党琰,贺平安. 利用Pearson相关系数定量分析生物亲缘关系[J]. 计算机工程与应用,2005(33):83-86，103.

[9] 李宏彬,赫光中,果秋婷. 基于皮尔逊相关系数的有机质谱相似性检索方法[J]. 化学分析计量,2015 (3):33-37.

[10] 王晓霞,徐晓钟,张彤,等. 基于集成深度学习算法的燃气负荷预测方法[J]. 计算机系统应用,2019 (12):47-54.

[11] 张豪杰. 基于HHT的电力负荷影响因素分析及预测(硕士学位论文)[D]. 郑州:郑州大学,2015:7-12.

[12] 刘海锋. 基于EEMD的GA-BPNN模型在大坝变形预报中的应用(硕士学位论文)[D]. 桂林:桂林理工大学,2018:28-33.

[13] 康志豪. 基于EEMD算法的电能质量扰动检测(硕士学位论文)[D]. 长沙:湖南大学,2016：18-24.

[14] ALLAHKARAM S R, ISAKHANI-ZAKARIA M, DERAKHSHANI M,et al. Investigation on corrosion rate and a novel corrosion criterion for gas pipelines affected by dynamic stray current[J]. Journal of Natural Gas Science and Engineering,2015,26:454-456.