生长单元在碾压混凝土结构仿真计算中的应用技巧

彭文明

(中国电建集团成都勘测设计研究院有限公司 勘测设计分公司， 四川 成都 610072)

1 研究背景

在碾压混凝土(roller compacted concrete，RCC)结构施工过程中，由于碾压层是逐层连续浇筑的，任何一个层合单元都有一个从空单元到实单元的过程，即层合单元位于施工面上的生长过程。在数值计算中模拟层合单元的上述动态变化，可以采用并层算法[1-2]、浮动并网[3-4]等技术手段。也有学者采用网格重构的方式，即混凝土位于施工仓面附近的新浇筑层，采用均质小单元划分网格，随着龄期变化，新浇混凝土变为老混凝土，将均质小单元与原有老混凝土大单元合并，即小单元均质网格合并成非均质层合单元。基于网格重构的做法，后续又发展了虚拟单元[5-6]或实体单元退化[7-8]的方式构建虚拟层合单元技术，同时也对非线性[9-10]、徐变应力[11-13]计算研究了数值分析实现手段。网格重构技术需要对模型重新划分单元，数值计算中并网的过程是人为调整的，会影响能量守恒，即人为地增加或减少单元能量，会影响计算精度。为此，学者们提出了模拟施工面上层合单元的另外一种技术手段，即生长单元法[14-15]，使用“生长单元”模拟施工面上层合单元的浇筑过程，使得模型网格可以一次生成，较好地解决了网格重构问题。

根据复合多层材料的单元模拟特点，学者们针对其层面问题开展了大量研究[16-19]，进一步揭示了层合(并层)单元的温度传播及力学机理，为单元模拟技术在大体积混凝土温控研究[20-21]、薄层结构设计[22]等方面的应用提供了基础，同时还对接缝或裂缝防控措施进行了广泛研究[23-25]。

从层合单元在数值模拟中的研究和应用实践可知，生长单元法可较好地解决网格重构的问题。在模拟碾压混凝土浇筑施工过程中，将碾压施工增加的混凝土层按次序并入生长单元，作为其实体单元的组成部分，在不增加单元数量的同时实现单元的“生长”变厚。当然，由于单元的材料层数较多，而且材料属性差异大，会导致一定的计算误差。与此同时，生长单元解决了大量网格重构的问题，但并入新浇筑层的当前单元，其节点几何坐标以及材料属性是动态变化的，并入新浇筑层后的计算初始值也应重置，需要采取相应的数值技术进行处理。

本文根据上述生长单元数值模拟的特点，研究多层材料的分段形函数方法，以及单元“生长”过程中的计算边界动态调整技术。

2 多层材料属性差异及影响分析

生长单元随着碾压浇筑层的上升而逐渐生长变大，因此生长单元与层合单元一样，包含多层材料层的生长单元如图1所示。

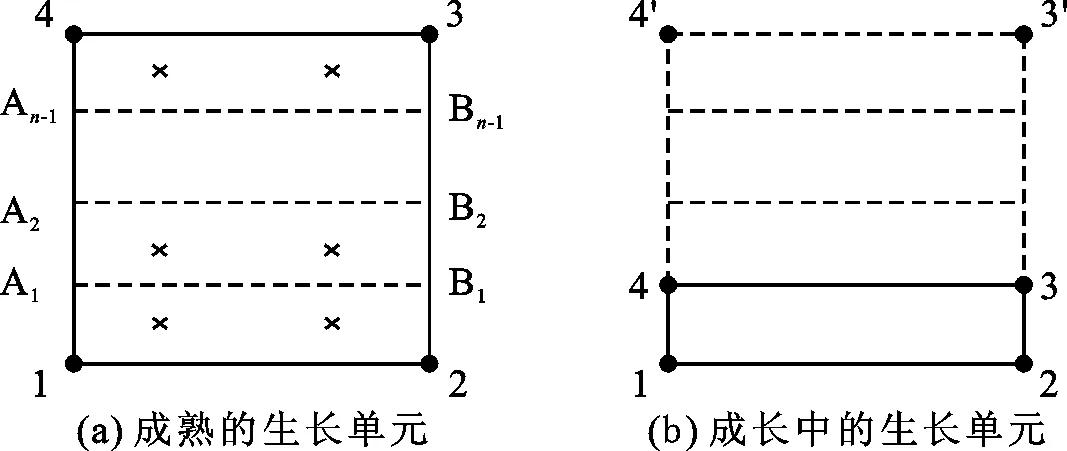
图1 生长单元示意图

由于浇筑时间有先后，生长单元内每层材料的混凝土龄期不同，导致各层材料的力学性能和热学性能随单元生长而变化。以混凝土的绝热温升和弹性模量为例，两者与混凝土龄期的关系曲线如图2所示。

图2 混凝土绝热温升及弹性模量与龄期的关系曲线

从图2可以看出，混凝土性能在早期变化很快，对包含多层不同龄期材料的生长单元而言，会对其有限元数值计算结果产生一定影响，下面通过举例分析说明。

例如，对于包含5个碾压层的生长单元，每层单元厚度为0.3 m，根据施工安排，碾压3层后进行仓面整理，相隔5 d后继续施工。对于该生长单元，在施工第5层混凝土时，下部先施工的3层混凝土龄期已经超过5 d。此时各混凝土层相应的龄期及性能指标如表1所示。由表1可见，当混凝土弹性模量E=E0(1-e-aτb)的参数取E0=41 GPa、a=0.46、b=0.38时，龄期5.4 d(第1层)的弹性模量约为24 GPa，与新浇混凝土(第5层)9 GPa的弹性模量相差很大；水化热温升按θ=25τ/(4.5+τ)计算，龄期5 d后各层最大温差超过11 ℃。当仓面上受到一定压力荷载作用时，在新浇混凝土两侧有老混凝土限制的情况下，各碾压层压缩变形量将相差较大。不同升程各碾压浇筑层混凝土的压缩变形及绝热温升如图3所示。

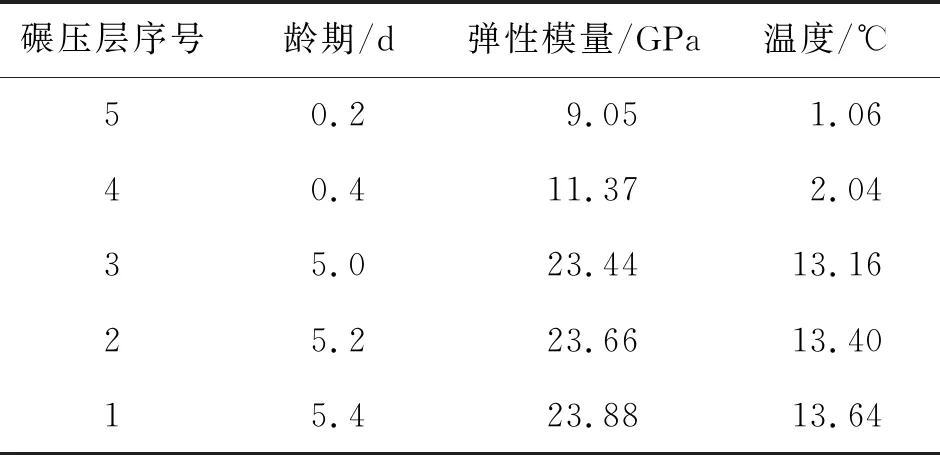
表1 不同升程各碾压层混凝土指标

图3 各碾压浇筑层混凝土的压缩变形及绝热温升

在有限元计算网格划分中，一个单元往往需要包含两个升程或更多。两个升程之间的间隔时间与仓面大小、混凝土输送、施工强度关系很大，相隔5～10 d是正常的，甚至可能会相隔30 d以上。根据上述分析，相隔5 d浇筑的混凝土，其材料属性在早期相差很大，从混凝土结构界面特性以及分层材料变形协调机理分析[26]，属性差异迥异的分层材料如果同时存在于一个单元中，对于有限元计算而言，须考虑材料属性差异大可能带来的计算问题。

3 分段形函数方法

由于生长单元内包含多层材料，在混凝土早期材料属性相差较大时，如果在温度和应力计算中采用双线性形函数表示，对计算结果可能影响较大。为此，本文提出生长单元分段形函数的计算方法。

计算中假定生长单元各层材料泊松比均相同，设为ν；对于厚度为ti的第i层材料，其弹性模量为αiE0(E0为常量)；设生长单元内平均应力为σ，每一层内应变为εi。则对于平面应变问题有：

(1)

其中：σz=ν(σx+σy)。

如图4(a)所示，建立整个生长单元的局部坐标系(ξ,η)，根据生长单元各层沿厚度方向的应变，可求解单元节点沿厚度方向的位移νi，以及各层界面Ai的位移νAi。

νAi=αiν1+βiν4

(2)

式中：νi为节点i的竖向位移，mm；αi、βi分别为形函数N1、N4在点Ai处的值，且αi+βi=1。

如图4(b)所示，从生长单元中取出第m层材料，以Am-1、Bm-1、Bm和Am为节点生成一个新的4节点等参单元，为区别于整个单元的局部坐标系(ξ,η)，取第m层材料的新单元局部坐标系为 (ξ′,η′)，并任取一点为P(ξ′P,η′P)。

图4 生长单元局部坐标系的建立

设P点在生长单元的局部坐标为(ξp,ηp)。当各层材料厚度处处相同时，局部坐标之间有如下关系：

ξ′P=ξp

(3)

按照常规4节点等参单元的位移场求解方法，第m层材料任一点P的位移为：

(4)

(5)

式中：ν′i为第m层材料各节点的竖向位移。

由公式(2)可得：

(6)

式中：αm-1和αm分别为N1在点Am-1和Am的取值； νi为图4中单元节点的竖向位移。

公式(6)可记为：

ν′=α·ν

(7)

由公式(4)、(5)、(7)可得：

(8)

由公式(8)可得：

阻尼系数比是评价悬架性能好坏的重要参数之一，是悬架“软”或“硬”的标志，也是振动衰减快慢的标志。为缓冲由不平路面传入的向上冲击，减振器的回弹(拉伸)阻尼力一般大于压缩阻尼力，其值在6比4-8比2。

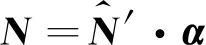
(9)

将公式(9)展开得：

(10)

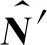
(11)

(η∈[ηAm-1,ηAm])

所以，图4所示的生长单元用分段连续函数表示为：

(12)

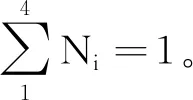
4 计算边界的动态调整

4.1 散热边界

生长单元位于当前单元网格最顶部，而且随着浇筑施工生长变厚，其散热边界的作用时间通常比较短，一个浇筑层顶向空气中散热常常仅发生在浇筑本层的过程中，当浇筑层上升时，原散热边界将被覆盖，同时又出现新浇筑层的散热边界。

在常规施工模拟中采用的是“生存期”算法，需要细致到对每个边界条件设定“激活”与“死亡”的时间，这项工作非常烦琐。本文针对RCC结构的特点，提出一种搜索替换和自动添加技术，能方便地解决上述问题。

虽然在RCC结构浇筑层上升过程中的散热边界更新替换非常频繁，但大部分情况下，一个旧散热面的消失是因为新浇筑混凝土层的覆盖，所以同时必定有一个新散热面产生。根据单元的空间拓扑关系，一般情况下总能找到新、旧散热面之间的关系，通过这种关系用新散热面替换旧散热面即为散热边界的搜索替换。

RCC结构施工过程中，浇筑层的顶面作为新的散热边界，是对底面覆盖的散热边界的进行替换，新旧浇筑层散热边界的演变如图5所示(如图5中散热边界②替换了散热边界①)，而大部分情况下浇筑层的侧面则是新增加的散热边界(如图5中的边界③和边界④)。对于一般的结构，散热边界往往是相连的。自动添加技术根据旧浇筑层的侧面散热边界，沿边界线在新浇筑层中搜索出新浇筑层的侧面，并自动添加到散热边界中。对每个浇筑层进行散热边界搜索替换和自动添加后，必须重新计算散热边界对荷载向量和热传导矩阵的影响。

图5 新旧浇筑层散热边界的演变

4.2 计算初始值

在生长单元计算过程中，由于碾压浇筑施工仓面的抬升，使单元“生长”后部分节点位置和材料属性发生了变化，需要重新赋值，包括节点的几何坐标、温度、位移和应力等计算值。

如图6所示，单元2675新添加一个浇筑层后，节点7和5的坐标在原节点7′和5′的基础上相应抬升。在上一步原节点7′和5′计算成果的基础上，根据计算的性质刷新赋值。对于温度计算而言，新浇筑混凝土应采用浇筑温度作为抬升节点的初始值；而生长的新节点位移和应力值，可根据上一步计算的位移场和应力场进行插值，如节点5，可根据原节点5′和节点3的位移值进行内插，得到新的节点5位移和应力初始值。但对于临空面的节点7，其位移初始值应与节点7′相同，即确保新浇混凝土不因初始位移形成初始应力；节点7的应力初始值应赋值为0。

图6 成长过程中的生长单元示意图

值得注意的是，调整生长单元初始值后，可能造成能量的损失。如图7所示，对于第i层界面的节点7′，上一步的计算温度为21.14 ℃，而根据节点6的计算温度43.46 ℃和节点7重新赋值的浇筑初始温度12.50 ℃，节点7′插值计算温度为18.67 ℃，显然新的温度场在该点有所降低，将引起局部计算误差。同样的问题，在节点5也存在。当然，根据圣维南原理，个别单元节点的计算误差对有限元整体计算影响不大。

图7 新增层计算初始温度值调整

4.3 过渡单元

在应用生长单元进行有限元计算时，由于生长单元在成长变化，相邻单元也要随之调整，可设置过渡单元，比如连接层合单元、接缝单元等。

(1)连接层合单元。在生长单元模拟浇筑施工过程中，与周围单元采用连接层合单元进行连接过渡，通常连接层合单元采用5节点等参单元，如图6中的单元12534。作为过渡单元，连接层合单元在生长单元“成长”过程中，代替相应位置的原有单元，并与生长单元相连，从而实现数值分析时有限元网格无“缝隙”。连接层合单元仅存在于相邻生长单元“生长”过程中，如图6所示，随着单元2675上部混凝土逐层浇筑而最终成为层合单元2673后，则连接层合单元12534完成其使命，恢复为相同位置的层合单元1234。设置连接层合单元后，计算过程仅需对有限元网格接缝连接部位进行单元替换，避免了网格整体重构，简化了有限元计算的工作量。

(2)接缝单元。生长单元为龄期较低的混凝土，与相邻老混凝土或基岩之间的弹性模量可能差异很大，接触面上由于热胀冷缩、渗水等影响，导致接缝面或浇筑层面抗拉强度降低甚至不能承受拉应力，只能传递压应力。为了考虑这一影响，段云岭等[27]提出材料非线性的接缝数值模型，通过设置接缝单元可以模拟混凝土结构工程交界面，而不考虑法向粘结作用。接缝单元除了可解决相邻单元材料性能差异大的过渡问题，也可解决生长单元调整新浇筑层计算初始值而造成的计算误差问题。

连接层合单元和接缝单元对有限元计算的几何特征、材料温度和受力协调等方面起到了很好的连接和过渡作用。

5 算 例

5.1 多层材料的挡水墙

图8为侧向受压的挡水墙模型，模型尺寸为2 m×4.5 m(宽×高)，底部与地基固定相连，挡水墙左侧受侧向水压。

图8 侧向受压挡水墙模型

设定挡水墙墙体竖向含50层不同混凝土材料，弹性模量从下到上由50 GPa递减到23 GPa，泊松比均取0.16，墙体厚度为1 m。对本算例采用两种网格划分模型：常规均质单元模型和多层材料的生长单元模型(本例无需计算生长过程)。用生长单元划分网格设定20个单元(每个单元10层材料)，30个节点(图8(a))；采用常规均质单元划分网格共需200个单元、255个节点。采用3种计算方案：(1)PATRAN方案，用商业软件MSC PATRAN &NATRAN对常规均质单元模型进行计算；(2)SLE方案，采用常规双线性形函数对生长单元模型进行计算；(3)MLE方案，采用分段形函数对生长单元模型进行计算。

在挡水墙高度分别为2.7和4.5 m处的水平截面D-D和E-E上提取界面各节点成果，图9为各节点不同计算方案的水平位移计算成果。

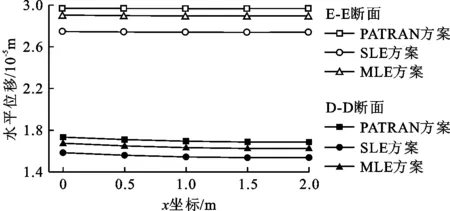
图9 D-D和E-E截面各节点不同计算方案的水平位移计算结果

由图9可以看出，SLE方案计算成果与其他方案偏离相对较大，是因为常规双线性形函数高估了单元的弹性模量，导致水平位移更小；MLE方案采用分段形函数的计算结果与均质单元的PATRAN方案计算结果更接近。对各计算方案的各节点计算结果进行误差统计对比，如表2所示。

表2 与PATRAN方案相比SLE、MLE方案的水平位移计算结果误差

由表2可知，与均质单元的PATRAN方案计算结果相比，由于单元内各层混凝土弹性模量差异较大，SLE方案采用常规双线性形函数产生的平均误差达到8.2%；MLE方案采用分段形函数算法，单元数量仅为PATRAN网格的1/10，其计算误差平均值仅为2.9%，表明分段形函数对计算精度有大幅提高。

5.2 多层浇筑块

多层浇筑块的计算模型如图10所示。模型由两个混凝土浇筑块Ⅰ和Ⅱ组成，每个浇筑块的几何尺寸均为宽3.0 m、高4.5 m。浇筑块逐层浇筑上升，每个浇筑层厚0.3 m，共15个浇筑层，层间间隔0.2 d；Ⅰ和Ⅱ浇筑块先后浇筑，连续浇筑上升直到本浇筑块浇筑完毕，浇筑完Ⅰ后间歇5 d再继续浇筑Ⅱ。

图10 多层混凝土浇筑块模型

多层混凝土浇筑块的材料热学参数见表3，绝热温升函数为θ=30τ/(2.3+τ)。假定浇筑块与地面绝热接触，其他面均向空气散热，空气温度和混凝土的初始温度均为10 ℃。

表3 多层浇筑块模型的混凝土热学指标

对浇筑块进行瞬态温度场分析。分别采用均质单元(总共60个单元)和生长单元(总共12个单元)对浇筑块进行划分网格计算(图10)，并进行浇筑过程的温度分析。图11为图10中所示的常规均质模型和生长连接单元中A、B、C 3个关键点的温度随时间变化的曲线。

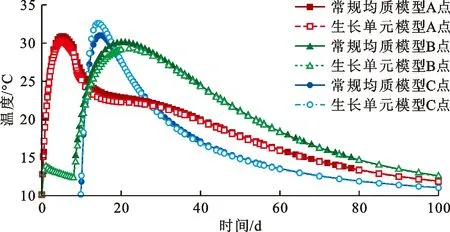
图11 多层混凝土浇筑块模型关键点温度变化曲线

由图11可以看出，生长单元模型与常规均质模型的温度计算结果非常接近，但两种模型的单元数量相差4倍，生长单元模型的计算效率高很多。浇筑施工到第9.2 d时，混凝土块Ⅱ已经浇筑了6层，此时的温度场分布如图12所示。对比两种网格模型算法，混凝土最高温度均为29 ℃，温度场总体分布规律基本一致。

6 结 论

(1)生长单元可较好地模拟RCC施工仓面的逐层上升过程，但单元内的多层材料对混凝土龄期很敏感。本文分析了生长单元各层碾压混凝土材料龄期相差5 d的绝热温升和弹性模量的差异，以及在外部荷载下的非线性变形特征，结果表明，此时采用双线性形函数描述生长单元已不合适。针对生长单元各层材料变形特征，对各层材料等厚度分布的碾压混凝土单元推导出的分段连续形函数表达式，可较好地描述因生长单元内材料差异大而导致的非线性变形问题，从而提高了计算精度。

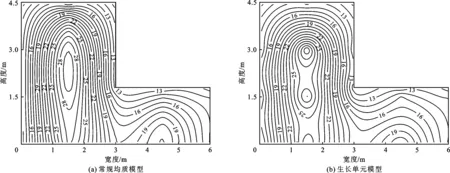
图12 多层混凝土浇筑块模型第9.2 d温度场分布(单位：℃)

(2)生长单元随着浇筑层的上升而生长，其计算边界需动态调整。本文提出生长单元散热边界的搜索与替换、新增层节点坐标及计算初始值重置、新老混凝土的单元连接等数值模拟技术，提升了生长单元在有限元计算中的应用范围。

(3)挡水墙算例验证了分段形函数方法在计算精度方面具有明显的优势，与常规均质单元计算结果相比，生长单元常规双线性形函数方法的计算平均误差为8.2%，而分段形函数算法的计算误差降低至2.9%。多层浇筑块算例则表明，应用计算边界动态调整技术后，生长单元能够顺利完成计算分析，其计算精度与常规均质单元基本一致，体现了本文方法的有效性。