长距离分洪隧洞输水模型试验相似性研究

余远浩， 张根广， 李安斌， 麻卉港， 封博研

(西北农林科技大学 水利与建筑工程学院， 陕西 杨凌 712100)

1 研究背景

近年来，随着我国输水调水工程的大规模兴建，长距离输水隧洞及明渠的应用已较为普遍。糙率作为隧洞和渠道设计的重要参数，其取值是否合理对于隧洞和渠道的过流能力及工程投资影响极大，因而输水建筑物糙率的计算问题得到广泛关注，并结合实际工程取得了大量的研究成果。比如，在南水北调工程中，王光谦团队对中线工程总干渠进行了糙率综合论证，推荐了各渠段的糙率系数并对糙率在一定范围内发生变化后对过流能力的影响进行了分析[1-3]；杨开林等[4]提出了渠道沿程糙率的系统辨识新方法，以中线工程观测资料为基础，得到了通用的渠道沿程糙率计算公式；郑和震等[5]对中线工程中的某一渠段采用了4种方法进行糙率计算，通过构建水力学数学模型进行检验后推荐出该工程糙率计算的最佳方法；陈文学等[6]提出了基于神经网络模型和粒子群优化方法进行糙率率定的方法，并以中线工程的某一渠段进行验证，验证结果较好。在引滦入津隧洞工程中，陈耀忠[7]对隧洞糙率进行了两次原型观测并得出了糙率的平均值为0.012 5；在引大入秦工程中，胡普年[8]对盘道岭长距离无压隧洞的糙率进行了原型观测，依据观测结果优化了除险加固设计，提高了隧洞过流能力并节省了大量工程投资。可见，糙率值的选取和计算为长距离输水工程设计的重要环节。

为验证隧洞的过流能力是否满足设计要求，通常采用物理模型试验进行验证[9-15]。但对于长距离隧洞来说，由于洞身较长，而受试验场地条件所限一般采用小比尺模型，从而难以保证模型的阻力相似条件，导致隧洞过流能力的试验结果有一定偏差。此问题的直接解决方法是打磨制模材料的过水壁面进行减阻处理，以实现阻力相似条件[16-17]。然而，对长距离隧洞模型，打磨壁面减阻的方法往往难以实现，因此，大多数学者均在既定的试验条件下，对试验结果进行理论修正分析以实现过流能力的相似。杨庆等[18]采用了变态模型试验和根据雷诺数与沿程阻力系数关系(Rem-λm)两种方法对模型试验过流能力进行修正，通过溪洛渡水电站导流隧洞工程的验证表明，导流隧洞修正后的进口过流能力是模型试验观测值的1.03倍；贺昌林等[19]依托某水电站泄洪洞工程，通过抬高库水位的方式来修正模型试验额外增加的沿程水头损失，实现了泄洪洞出口流速和流量的相似，修正后的泄洪洞过流能力是模型试验观测值的1.07倍；吕宜卫[20]根据水流能量方程和连续性方程，充分利用局部阻力观测结果和沿程阻力理论分析成果，将模型试验与理论分析相结合，提出了糙率偏差对应的修正公式，结合小浪底导流洞模型试验，导流隧洞修正后的过流能力同样是模型试验观测值的1.07倍；苗宝广等[21]利用有压长隧洞洞内沿程水头损失的变化值修正上游水位，实现洞内过流能力的相似，试验修正值与原型观测值吻合良好，可以很好地满足工程需要；郑小玉等[22]通过贵州省某水电站溢洪道水工模型试验，提出了水工模型试验中糙率修正的一种新观点，即对已测量的数据进行分析，根据工程需要精度来判断糙率修正的必要性，以此提高工作效率；阎庆绂等[23]结合引黄入晋工程，通过分析流速分布和水面线的不相似问题，提出了阻力相似修正系数K，结果表明，对模型试验数据进行修正是可行的。黄纪忠等[24]基于明渠定床清水模型，提出了采用模型坡降、几何变态以及糙率延伸等方法进行模型试验以实现阻力相似。

上述对小比尺物理模型试验的相似性研究，大都是基于有压流段以局部阻力和沿程阻力为入手点，通过修正隧洞进口水位来补偿模型试验中额外增加的水头损失，以实现对隧洞原型过流能力的相似验证，而对于无压流模型试验的相似性验证研究较少。本文基于陕西省某长距离分洪明流隧洞，对小比尺模型试验相似性进行了分析与探讨，通过对分洪隧洞进口闸室段过流能力和隧洞段输水能力分段进行试验研究，实现了在小比尺物理模型上进行无压流隧洞过流能力的试验相似性验证。

2 工程概况

陕西省某县城分布于某河流两岸，城市挤占河道现象严重。主城区河道狭窄，边界条件复杂，现状河宽为52～70 m，且河道县城段呈“上下宽、中间窄”，泄洪能力严重受限。为保证县城30年一遇防洪安全，在主城区上游支流布置了分洪工程。经过对多重因素考虑后，支流分洪工程在张家砭镇马家洼村河道的凹岸布置分洪口，穿县城南侧山体布置分洪隧洞，出口位于名州镇芋则沟村，分洪工程示意图见图1。设计要求通过分洪隧洞将支流30年一遇洪水流量4 540 m3/s中的800 m3/s直接分流至干流主城区段的下游，以减轻该河流两岸主城区的防洪压力，确保县城30年一遇防洪安全。

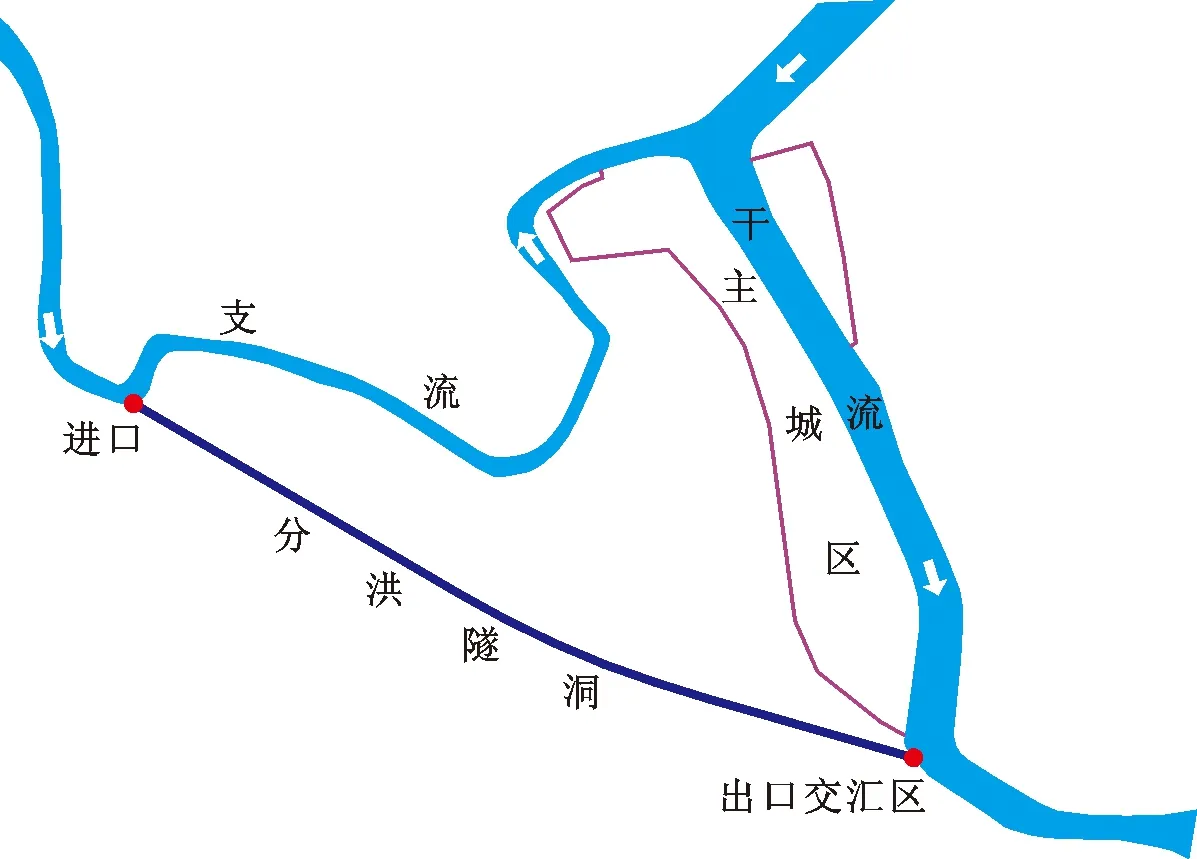
图1 某县城分洪工程平面示意图(单位：m)

分洪隧洞由进口段(桩号0-042.11～0-015.00 m)及闸室段(桩号0-015.00～0+000.00 m)、上游直段(桩号0+000.00～2+203.00 m)、中间弯道段(桩号2+203.00～3+438.28 m)、下游直段(桩号3+438.28～4+602.00 m)以及出口段(桩号4+602.00 m～4+676.50 m)5部分组成。分洪隧洞进口为喇叭口布置，底板高程为815.00 m，在桩号0-010.00 m处布设闸门，洞身横断面设计为马蹄形，纵坡坡降为3.06‰，全长4 718.61 m。出口为防止干流河水倒灌而设置了防洪闸，闸底板高程为802.00 m。为保证安全分洪，在分洪进口上游约900 m范围河段的左、右岸修建了堤防工程，其设计防洪标准为河道30年一遇。分洪隧洞平面布置见图2。

图2 分洪隧洞平面布置图(单位：m)

3 模型相似性设计分析

为保证试验精度，准确反映原型水流情况，模型试验应既要保证分洪隧洞进口流态相似，同时又要充分反映进口分流效果。试验模型主要包括1 500 m长度的干流河段及支流分洪隧洞。

由于原型分洪隧洞长4 718.61 m，糙率为0.014，若要模型与原型完全满足水流运动相似，就常用的制模材料来看，模型几何比尺应该在λL=λH=15～20之间，仅分洪隧洞模型长度就达到200 m以上，模型场地难以满足。因此模型相似设计放弃阻力相似条件，而采用对进口闸室段过流能力及隧洞段输水能力分别验证的方法，这主要是基于以下两个方面考虑：隧洞段内可以形成均匀流，采用明渠均匀流计算方法对实测结果进行计算验证；进口闸室段距离短、局部损失远大于沿程阻力损失，沿程阻力损失可以忽略，控制进口闸室出口水深为隧洞正常水深可直接验证进水闸室段过流能力。

鉴于上述分析，试验采用正态模型设计，几何比尺λL=125，相应的其他主要物理量的模型比尺见表1，为了对比，表1中还列出了几何比尺λL=15时相应的其他主要物理量模型比尺。

表1 两种几何比尺相应的主要参数模型比尺

已知原型河道段糙率为0.033，分洪隧洞糙率为0.014。模型河道的河床及边坡均为定床，采用水泥抹面，糙率约为0.014，可满足与原型糙率相似；模型分洪隧洞制作材料为有机玻璃，糙率为0.009，对应的原型糙率为0.020，比原型分洪隧洞糙率0.014增大了约43%。

4 结果与分析

4.1 长隧洞段过流能力验证

基于对隧洞过流量和工程经济成本的考虑，模型试验共进行了隧洞不同体型及坡降的3组方案对比试验。各方案具体设计参数见表2。

表2 隧洞段不同试验方案的设计参数

在河道防洪标准为30年一遇工况下，通过完全开启分洪隧洞进口闸门，对3组方案进行过流能力试验。试验观测发现，进入闸室的水流经过闸室段及一定长度的隧洞段调整后，水流在分洪隧洞内均能形成稳定均匀流，观测到方案1的均匀流正常水深为7.25 m，方案2的均匀流正常水深为12.50 m，方案3的均匀流正常水深为8.60 m。基于洞内观测的正常水深值，依据明渠均匀流计算方法按公式(1)、(2)计算隧洞段的过流量，计算结果与模型试验实测值的比较见表3。

表3 各试验方案分洪隧洞过流量的计算值与模型实测值比较

Q=A·V

(1)

(2)

式中：所有参数均为原型值。Q为隧洞计算过流流量，m3/s；A为隧洞过水断面面积，m2；n为糙率；R为水力半径，m；i为隧洞坡降。

由表3可知，河道30年一遇洪水工况下，与模型糙率0.009相匹配的原型隧洞计算过流量与模型实测过流量基本一致。在不同试验方案下，计算所得的过流量与实测过流量最大差值为29.71 m3/s，最大相对误差为7.9%；最小差值为11.71 m3/s，最小相对误差为1.93%，且从方案1到方案3，模型实测流量与计算流量的差值逐渐减小，究其原因，方案1为第1观测试验，在模型试验实测河道和隧洞的过流量时，水流没有达到完全平稳，因此误差较大；在方案2、方案3的测量中，观测过程得以尽可能的延长，以确保模型河道和隧洞过流稳定，因此实测值与计算值的差值减小。上述分析表明，根据物理模型观测的正常水深及明渠均匀流计算方法，可以准确计算原型分洪隧洞的过流量。

同理，依据明渠均匀流计算方法可计算得到各试验方案隧洞糙率分别为0.020、0.014的过流量，计算结果见表4。

由表4可知，不同试验方案下，糙率为0.014的实际过流量均较糙率为0.020的过流量增大了43.7%。方案2、3的最大过流量分别可达962.79、887.94 m3/s，大于设计要求的过流量800 m3/s。

表4 各试验方案分洪隧洞糙率为0.020和0.014的计算过流量

4.2 进口闸室段过流能力验证

考虑到隧洞进口闸室段较短，属于急变流段，沿程阻力损失相对局部阻力损失可以忽略不计。水流经过闸室段调整，在隧洞桩号0+099.25 m断面基本形成均匀流，因此以此断面作为控制断面，控制该处水位为洞内观测的正常水深，以验证隧洞进口过流能力，闸室至隧洞桩号0+099.25 m断面水流流态见图3。

图3 闸室至隧洞桩号0+099.25 m断面水流流态(试验方案3)

首先从理论上分析计算进口闸室段过流能力，并结合实测资料进行分析比较及验证。针对方案3的马蹄形过水断面，选取闸室进口前沿桩号0-042.11 m处断面为1-1断面、洞身段桩号0+099.25 m处断面为2-2断面(见图1、3)，进行过流能力理论分析计算及验证。在给定河道30年一遇工况洪水条件下，控制2-2断面水深为隧洞实测正常水深，并以2-2断面出口底板高程为基准面，列出1-1断面与2-2断面水流能量平衡方程为：

(3)

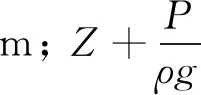
根据方程式(3)及水流连续性方程，可计算出隧洞进口闸室段过流量，计算值与模型实测结果比较见表5。

由表5可知，进口闸室段沿程水头损失小于局部水头损失；在进口闸室底板高程为811 m时，实测过流量与计算过流量的差值为18.53 m3/s，相对误差为1.78%；在进口闸室底板高程为815 m时，实测过流量与计算过流量的差值为9.91 m3/s，相对误差为1.64%。说明忽略沿程水头损失对计算结果影响较小，采用此方法直接验证进口段过流能力是可行的。

表5 不同试验方案进口闸室段过流量计算值与模型实测值比较

根据上述分析计算方法，对进口闸室底板高程及隧洞坡降进行了调整，并对闸室过流量与隧洞段过流量进行了匹配计算，最后确定闸室底板高程812.6 m、坡降2.55‰作为推荐方案。在30年一遇洪水时，推荐方案糙率为0.014的闸室过流量与隧洞过流量匹配计算结果见表6、7。

表6 推荐方案闸室过流量计算结果(糙率n=0.014)

表7 推荐方案闸室过流量与隧洞过流量匹配计算结果(糙率n=0.014)

由表6、7可知，在闸室底板高程为812.6 m时，隧洞过流能力与闸室过流量基本匹配一致，分洪流量为863 m3/s，较设计过流量800 m3/s超泄了63 m3/s，占设计过流量的7.88%，满足设计要求。经模型试验实测资料验证，计算的分洪流量与实测值基本一致。

5 结 论

本文基于陕西省某县城长距离分洪隧洞输水模型，通过对进口闸室段过流能力及隧洞段输水能力分别验证，实现了在小比尺物理模型上进行隧洞过流能力的试验验证，得出的主要结论如下：

(1)基于隧洞段内可以形成均匀流的特点，采用明渠均匀流计算方法并结合曼宁公式，对计算得到的过流量与其糙率相似匹配的原型隧洞的过流量进行分析对比，在模型观测流量较为稳定的情况下，两者的流量差值最小为11.71 m3/s，最小相对误差仅为1.93%。说明该模型设计制作及观测结果无误，均匀流计算方法可以准确计算原型分洪隧洞的过流量。

(2)基于隧洞进口闸室段距离短、局部阻力损失远大于沿程阻力损失的特点，控制隧洞桩号0+099.25 m处水深为隧洞正常水深，经理论分析计算得出的进口闸室段过流量与实测过流量基本一致，最大相对误差不超过1.78%。

(3)对隧洞进口闸室底板高程及洞身坡降进行了调整优化，最后确定闸室底板高程812.6 m、隧洞坡降2.55‰作为推荐方案。在30年一遇洪水时，推荐方案闸室和隧洞洞身的过流量相匹配且与模型实测值基本一致，分洪流量达到863 m3/s，较设计分洪流量800 m3/s超泄了63 m3/s，超泄流量占设计过流量的7.88%，完全满足设计要求。