耦合NSGA-Ⅱ算法与高精度水动力模型的LID设施优化设计方法研究
2022-08-30张文晴侯精明王俊珲周思敏李智星李东来
张文晴, 侯精明, 王俊珲, 周思敏, 李智星, 李东来, 张 松, 杨 霄
(1.西安理工大学 西北旱区生态水利国家重点实验室, 陕西 西安 710048; 2.四川水利职业技术学院,四川 成都 611845; 3.中国电建西北勘测设计研究院有限公司, 陕西 西安 710065)
1 研究背景
近年来,随着极端天气的频发以及城市化进程的快速发展,城市地表不透水率逐年升高,下垫面渗水能力不断降低,雨水无法及时下渗,导致城市内涝问题十分严重[1-4]。为了应对此类城市问题,我国基于低影响开发(low impact development, LID)理念,提出了“渗、滞、蓄、净、用、排”的海绵城市雨洪管理新概念,在不大幅度影响城市原生态的情况下,通过人工设施调节过量雨水,即通过新建LID设施的方式降低城市的雨洪风险[5-9]。
为精准有效地实现城市雨水的管控,需要对LID设施建设方案进行优化设计研究[10-15]。周昕等[16]通过设置不同的LID设施组合方案对区域雨洪控制效果进行了模拟研究,得到了不同LID设施组合对研究区域雨洪调控的量化效果。李莹等[17]基于暴雨洪水管理模型模拟计算了城市传统开发和LID两种模式的雨洪过程,采用多元回归法建立了LID布设比例与径流总量及建设成本之间的关系函数,以最低成本削减最多洪量为目标,得到了LID设施建设比例与建设效果的优化方案。孙会航等[18]基于NSGA-Ⅱ算法利用暴雨洪水管理模型(storm water management model,SWMM),以某区域为例,构建了一套建设成本最小化、水文水质效益最大化的设计方案,定量地得到了海绵城市建设效果。
此类研究大都利用水文学的方法对区域LID设施建设后的雨洪控制效果进行模拟评估。采用水文学的方法对LID设施的输水过程进行模拟,有着较为清晰的物理意义表达。然而水文学方法在对二维地表的产汇流过程进行模拟计算时,模拟结果大都仅能得到流域出口处的流量过程,无法给出特定位置的水力特征要素,并且由于水文模型存在对复杂地形描述能力较弱、对参数经验依赖性较强等问题,影响着模拟结果的准确性[19-20]。
为了弥补传统水文模型模拟计算上的不足、能够直观地评价LID设施的建设效果、得到效果更佳的LID设施优化设计方案,本文利用模拟城市洪涝过程的一、二维耦合数值模型,基于NSGA-Ⅱ算法提出了一种LID设施优化设计方法。该方法通过耦合二维地表与一维管网的高精度数值模型模拟LID设施不同建设工况下的城市积涝情况,再将LID设施建设面积与建设效果进行函数拟合得到经验公式,而后将经验公式进行NSGA-Ⅱ算法的迭代计算,最终得到LID设施优化设计的建设成本与建设效果系列优化方案解集,并对各建设成本下单项及组合LID设施建设规律进行了相关分析,得到LID设施建设成本与建设效果间的相关规律,为城市LID设施建设及雨洪调控提供了一套适用性强的新方法。
2 LID设施优化设计方法
2.1 一、二维耦合水动力数值模型
2.1.1 二维地表水动力模型 二维地表水动力部分以二维浅水方程作为控制方程,方程忽略运动黏性项、紊流黏性项、风应力和科氏力,二维非线性浅水方程矢量形式如下[21-22]:
(1)
(2)
(3)
(4)
(5)
式中:q为变量矢量;h为水深,m;qx、qy分别为x、y方向的单宽流量,m3/( s·m );g为重力加速度,m/s2;u和v分别为x、y方向的流速,m/s;F和G分别为x、y方向的通量矢量;S为源项矢量;i为入渗和降雨源项;zb为底面高程,m;Cf为谢才系数,Cf=gn2/h1/3,m1/2/s;n为曼宁系数,m1/3/s。
对区域进行网格化离散时,为尽可能提升计算精度,采用Godunov格式的有限体积法进行空间离散,并采用HLLC(Harten-Lax-van Leer-contact)近似黎曼求解器处理计算单元界面上质量通量与动量通量的急变流与非连续问题;对于水动力模型常见的在干湿边界处的负水深问题,通过静水重构的方法进行处理;将易失稳的二阶格式在水深低于或流速高于特定值时转换为稳定的一阶计算格式,以此保证模型计算时的稳定性[23-24]。为了在保证计算精度的同时大幅提升计算效率,引入图形处理器(graphics processing unit,GPU)技术对模型进行加速计算[25-26]。
城市不同下垫面的下渗能力采用地表水动力过程的Green-Ampt入渗模型的基本表达式来表征,该公式能表达持续降雨时不同下垫面的真实渗水能力,将该公式与二维地表水动力模型进行耦合求解,即可得到地表水动力模型不同下垫面属性网格单元上准确的产汇水信息。Green-Ampt模型的基本表达式如下[27]:
(6)
式中:fp为入渗率,cm/min;Ks为饱和导水率,cm/min;θi和θs分别为初始含水率及饱和含水率,cm3/cm3;Sf为湿润锋面吸力,cm;tp为降雨后开始积水的时间,min;R为降雨强度,cm/min;Ip为累计入渗量,cm,Ip=tpR。
2.1.2 一维管网水动力模型 一维管网水动力过程的模拟按实际物理过程可分为未完全充满水时的无压流和完全充满水时的有压流状态,对管道的输水过程的模拟计算方法决定了一维管道水动力模型模拟的计算精度。因此,对一维管道模型分为明渠无压流和管道有压流两种流态进行模拟计算,流态的判别方法由管道的充满程度判定。两种流态的计算方法如下所示:
(1) 明渠无压流。管道的明渠无压流流态采用曼宁公式计算管道流量,计算公式如下:
Q=A·R2/3·J1/2·n-1
(7)
式中:Q为管道流量,m3/s;A为管道中过水断面面积,m2;R为水力半径,m;J为水力坡降;n为管道糙率。
(2)管道有压流。管道的有压流流态通过一维Saint-Venant方程来模拟求解,求解过程忽略惯性力的作用,该方法解算精准快捷并且可以较好地反映水流在管网中的运动特点。数值离散方法采用有限差分法。管道有压流求解方程如下:
(8)
(9)
式中:A为管道过水断面面积,m2;Q为管道流量,m3/s;t为时间,s;s为固定横截面沿程的距离,m;g为重力加速度,m/s2;Sf为摩阻比降,Sf=Q|Q|·n2/(A2·R4/3)。
2.1.3 一维、二维水动力模型耦合方法 一维管网与二维地表主要通过雨水井等汇水节点进行耦合计算,地表汇入雨水井的水量采用下列堰流公式或孔流公式计算:
(10)
式中:Qin为地表水汇入管网的流量,m3/s;cw为堰流系数;co为孔流系数;Ci为雨水井入口的周长,m;g为重力加速度,m/s2;h2D为地表水深,m,其中h2D=Z2D-Z1D;Zb2D为地表高程;Z2D为地表水位,m;Z1D为雨水井内水位高程,m;Ai为雨水井入口截面面积,m2。
当雨水井中的水深超过地表水高程而发生地表溢流时,溢流量采用下列孔流公式计算:
(11)
式中:Qout为从雨水井溢流至地表的溢流流量,m3/s。
2.2 LID设施概化方法
LID设施根据传输过量雨水的不同特性可分为源头削减型LID设施、过程传输型LID设施、末端蓄存型LID设施。本文主要研究源头削减型LID设施,如透水铺装、雨水花园、绿色屋顶等的优化设计方法。源头削减型主要通过其强大的下渗能力削减过量雨水,以达到减少径流和积涝的目的。因此针对源头削减型LID设施的特点,本研究设计方案中对LID设施的建设效果模拟主要通过调整其面积及下渗参数概化得出。水动力模型中对LID设施的面积表征可以具体、量化地在土地利用类型中体现,相较于水文模型中对LID设施的表征仅为汇水分区内的面积占比,水动力模型的模拟结果能够完整地描述LID设施建设后的产汇流过程,其模拟结果更为准确。对LID设施下渗过程的描述仍采用Green-Ampt入渗模型表征,入渗公式如公式(6)所示,相关参数可实际测得或参考当地标准规范。
2.3 LID设施布局方法
主要布局方法为:(1)利用一、二维耦合水动力模型模拟出研究区域未布设LID措施时的积涝情况,得到原始条件下的积涝风险图;(2)根据积涝风险图中局部内涝严重区域,结合地籍属性、重要性级别或实际工程需求,选出若干个LID设施初始建设起点;(3)以这些初始建设起点为中心依次向外规律性地增设相应的LID措施,直至达到LID设施可建的最大范围,得到各种建设面积工况下的地表积水情况。

图1 LID设施增设布局方法示意图
2.4 NSGA-Ⅱ优化算法
NSGA-Ⅱ算法(non-dominated sorting genetic algorithm-Ⅱ),即第二代改进后的非支配多目标优化算法,相比第一代NSGA算法,由于增加了快速非支配排序算法,其计算效率更高;该算法采用了拥挤度比较算法,使计算结果能均匀分布于整个Pareto域;并且,由于精英策略算法的引入,在提升运算速度的同时扩大了计算采样空间,极大地提高了最佳个体的采样率,因而该算法能够在相关领域得以稳健应用[28]。
由于NSGA-Ⅱ算法能全面地输入各类线性、非线性、一元或多元函数,并且其对各种约束条件具有较好的适应性,使得该算法在工程最优化求解方面有着广泛的应用。需要注意的是该算法只存在最优解集而不是单个最优解,解集中的解无法比较优劣,称为非劣解或非支配解,其特点是无法在改善任何目标函数的同时又不削弱其他任意目标函数的非支配排序。此种特性使得结果存在多样化,决策者可根据具体的工程实际需求在解集中寻得相对最优解。
(1) LID设施费用函数
f1=Ai·Wi
(12)
式中:Ai为第i种LID设施建设面积,m2;Wi为第i种LID设施建设单价,元/m2。
(2)地表峰值积水削减量函数
f2=F0-f(Ai)
(13)
式中:F0为LID设施建设前地表峰值积水时刻总积水量,m3;f(Ai)为第i种LID措施建设后地表峰值总积水量,m3。
标准化处理后,即得比较数列xi={xi(k)|k=1,2,…,6},i=1,2,…,55。取各指标的最大值,得到虚拟最优单株,即参考数列x0={x0(k)|k=1,2,…,6}。
(3)耦合水动力模型的LID设施优化设计总目标函数
(14)
(4) 约束条件
在实际工程中,LID设施建设范围是一定的,因此需要对优化模型进行相应的面积条件约束。雨水花园改建面积主要取决于城市的绿地及建筑周围的可用空地,透水铺装的改建面积取决于城市的人行交通道路及广场等设施的面积,可以根据研究区域内相应设施确定出如下的LID设施约束条件。
(15)
式中:A1、A2为透水铺装和雨水花园实际建设面积,m2;A1 max、A2 max为研究区域内透水铺装和雨水花园可建最大范围,m2。
2.5 LID设施优化设计步骤
(1)建立用于求解LID优化设计解集的耦合水动力模型,包括所需的地形高程、降雨、下渗和若干LID设施增设工况的地籍文件。
(2)在耦合水动力模型中运行全部输入文件,得到相应的城市雨洪过程计算结果。
(3)以计算结果中峰值积水时刻的积水削减量作为LID设施建设效果的评价指标,用未建设LID工况下的峰值积水量减去各LID建设工况下的峰值积水量,得到各LID建设工况相比未建设LID措施的峰值积水削减量。
(4)以LID建设面积为自变量,各建设工况的峰值积水量削减量为因变量,拟合LID建设数量与水量削减量之间的经验公式。
(5)以最小建设成本和最大峰值积水削减量为优化目标,采用NSGA-Ⅱ算法计算得到LID建设最佳优化设计效果与建设成本之间的帕雷托(Pareto)最优解集。
(6)根据实际需求选出Pareto解集中满足工程、经济条件的相应解,即为LID最优布局的决策解。
3 实例优化设计与结果分析
3.1 研究区域概况
为验证该方法的实际应用效果,选取陕西省西安市西咸新区部分核心区域作为研究区域。该区域属典型的半湿润大陆性季风气候,夏季雨水集中,且多以暴雨形式出现,易造成洪、涝等自然灾害[29]。研究区域总面积为1.08 km2,区域内建筑密集、地籍类型多样、路网纵横交错、下垫面情况复杂,具有典型的城市化属性,在该区域开展LID设施优化设计研究具有一定的代表性。研究区域概况如图2所示。
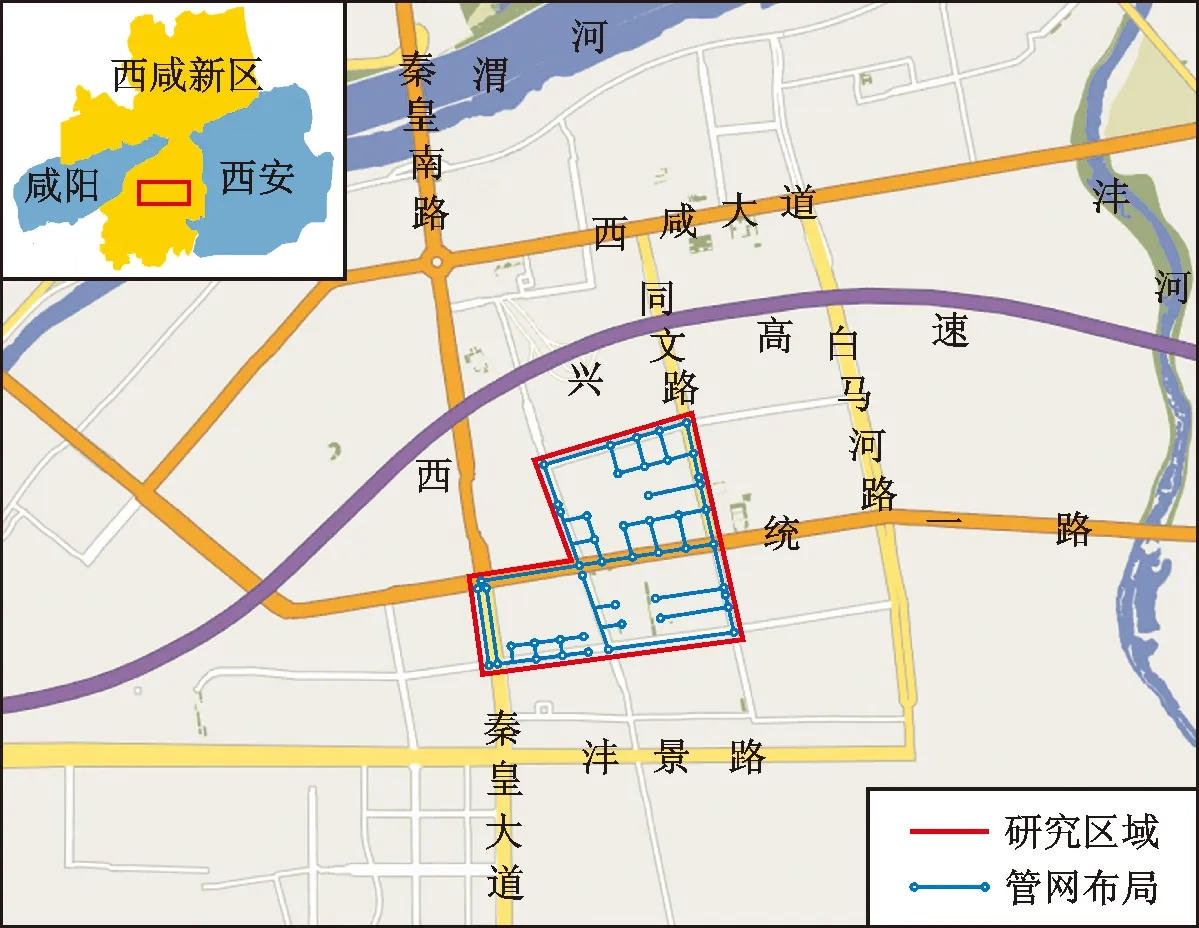
图2 研究区域概况
3.2 耦合水动力模型构建
本文采用耦合了一、二维水动力过程的高精度数值模型对研究区域的内涝积水过程进行模拟,模型的输入条件包括:降雨数据、地形数据、土地利用类型数据、下渗数据、管网数据及其他模型参数。
降雨数据采用具有当地特征降雨属性的西咸新区暴雨强度公式,如公式(16)所示,可得到模型所需降雨文件。根据学者们的相关研究结论,LID设施一般对中低重现期雨洪的调控效果较为明显,高重现期情景下的调控效果较差[30]。因此,本文采用5年一遇降雨重现期下总降雨时长为2 h的芝加哥设计降雨资料作为本文的主要输入降雨数据[21]。
(16)
式中:q为暴雨强度,L/(s·hm2);P为重现期,a;t为降雨历时,min。
地表水动力模型中网格的精细程度决定了模拟结果的准确度,为得到研究区域内的精确数值模拟解,采用无人机航测技术对研究区的地形高程进行巡航测算,得到输入网格精度为1 m的高精度DEM(digital elevation model)数据,研究区域地形高程数据如图3所示。

图3 研究区域地形高程数据
模型所需的地籍文件通过对研究区域正射影像图进行极大似然分类,共分为建筑、道路、裸土、林地、草地5种不同的土地利用类型。为体现典型LID设施的布局优化效果,本文基于城市海绵建设低影响开发理念,选出对产汇流过程影响较大的两种LID措施:透水铺装和雨水花园,进行优化模拟布局研究。每种地籍属性的下渗过程用Green-Ampt模型描述,根据相关文献及经验值确定的各土地利用类型的下渗参数如表1所示。

表1 各土地利用类型的下渗参数
LID设施优化设计研究主要以LID设施在不同增设工况下的积水量模拟结果作为优化基础。根据数值模型的模拟结果,5年一遇降雨重现期下,t=3 000 s时地表积水量达到峰值。因此,各LID设施建设工况的雨洪调控效果用该时刻的地表总积水量表征。对于未布设LID设施前的区域内涝风险图,亦采用该时刻积水情况表征,得到地表最大内涝风险图如图4(a)所示,同时结合地籍属性确定出如图4(b)所示的LID设施起始建设点。

图4 研究区域内涝风险图及LID设施建设起点
对LID设施进行增设扩建时,需同时对3个建设起点进行各单种及组合LID措施在不同建设面积工况下的增设,直至达到最大允许增设面积。本次研究对单种LID措施增设5次,最终可以得到透水铺装和雨水花园单项措施的各6组模拟结果,以及两种LID设施建设工况组合下的36组模拟结果。
为切合LID理念,体现因地制宜的建设效果,将城市建设对原生态的影响降到最低,LID设施的建设方法为:将原始土地利用类型中的草地和建筑附近的裸土新建成雨水花园;将道路和建筑以外的裸土建设成透水铺装。由于城市主干道承载着繁重的交通运行任务,若替换成透水铺装则日常维护成本巨大,且对原有的交通运行影响较大,因此对区域内交通主干道不做LID设施改变。由此得到透水铺装的最大建设面积为225 622 m2,雨水花园的最大建设面积为135 175 m2,依据前文2.4节中的约束条件将此作为优化模型的最大建设面积上限。
3.3 优化模型
根据模型模拟结果得到如表2所示的LID设施建设面积与区域峰值积水削减量的数据对应关系。

表2 不同LID设施建设工况模拟结果
为定量表征LID设施的建设规律,需要根据模型所得数据对单项及组合LID设施作用下的建设效果进行合理的公式拟合,得到能适用于NSGA-Ⅱ算法的经验公式。同时,为评价拟合公式的准确性,采用决定系数R2验证拟合函数与模拟数据间的拟合程度。对于单项布局的LID措施,根据优化设计的方法可知,建设面积与减少水量的曲线函数应该大致为正相关的非线性关系,因此可采用二次多项式函数表征单项LID设施面积与峰值积水削减量之间的曲线关系,单项LID设施拟合函数曲线如图5(a)、5 (b)所示。对于组合布局的LID措施,自变量为两种单项LID设施的建设面积,因变量为削减的水量,由于此拟合函数为二元函数,函数表征复杂性较强,因此选择常见的曲面模型进行数据拟合,最后选取R2最大的Lorentz模型来拟合组合LID设施的建设面积与峰值积水削减量之间的函数关系式,组合LID设施拟合函数图如图5(c)所示。各拟合公式及决定系数R2见表3。
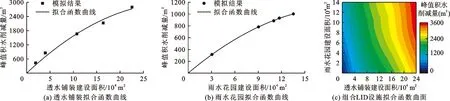
图5 各单项及组合LID措施的建设面积与峰值积水削减量关系拟合函数曲线(曲面)

表3 LID设施建设面积与峰值积水削减量关系拟合公式及决定系数
由于拟合函数均为非线性函数,导致优化过程计算量庞大。为了确保优化目标函数值精确、均匀分布的同时又尽量节省运算时间,采取如表4所示的NSGA-Ⅱ优化参数。

表4 NSGA-Ⅱ优化参数取值
优化模型的LID设施建造价格参考《海绵城市建设技术指南》及同等经济水平城市实际建设案例[19],确定透水铺装单价为200元/m2,雨水花园单价为500元/m2。
3.4 优化结果与分析
通过NSGA-II算法对研究区域LID设施成本及雨洪调控效果进行优化求解,得到了若干单项及组合LID设施建设方案的Pareto最优解集,优化模型计算结果见图6,其中每个最优解均包含相应LID设施的建设面积、总建设成本和峰值积水削减量。为准确评价优化算法所得解集中LID设施的城市雨洪控制效果,对各单项及组合LID措施分别按建设成本由小到大选择3个方案进行比对分析。
3.4.1 单项LID设施优化结果分析 对于图6(a)中透水铺装的优化解集,选取方案1的建设成本和峰值积水削减量分别为4 164 400元、366.38 m3;选取方案2的建设成本和峰值积水削减量分别为19 405 800元、1 527.02 m3;选取方案3的建设成本和峰值积水削减量分别为36 750 300元、2 438.95 m3。对于图6(b)中雨水花园的优化解集,选取方案1的建设成本和峰值积水削减量分别为4 892 250元、106.85 m3;选取方案2的建设成本和峰值积水削减量分别为28 484 000元、544.6 m3;选取方案3的建设成本和峰值积水削减量分别为56 378 800元、906.7 m3。将透水铺装和雨水花园建设成本由低到高进行建设效果分析,单项LID设施各方案的优化解效果对比见图7。

图6 各单项及组合LID设施Pareto解集
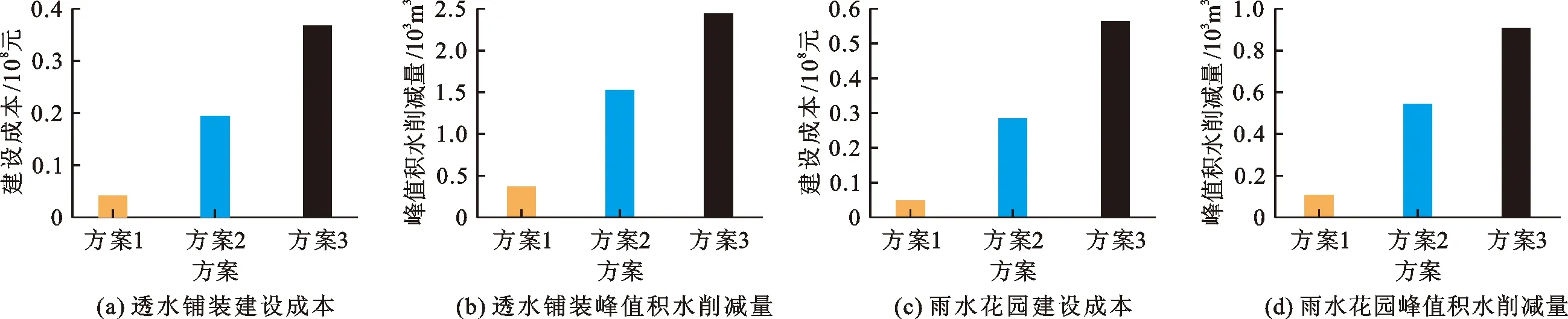
图7 单项LID设施优化结果对比分析
由图7可知,对于单独建设的两种LID设施,在低成本建设方案下,由于LID设施建设的数量有限,对城市雨洪的调控效果也达不到理想要求,但随着LID设施建设面积与成本的增加,城市降雨峰值时刻的积水量也随之减少,若决策者需要对城市进行单项LID设施建设,可以根据具体的工程需求与实际情况选择优化解集中的实际最优解对城市进行相应的改造建设。
然而,若仅布设单项LID设施具有较大的局限性,并且单项LID设施城市的雨洪调控能力也是有限的,由于各种LID设施的性质不同,雨洪调控的效果也有很大差异。在本研究区域中最大透水铺装建设面积下的峰值积水削减量为2 796.8 m3,最大雨水花园建设面积下的峰值积水削减量为1 003.1 m3,而组合LID设施最大建设面积下的峰值积水削减量为3 443.4 m3。因此在区域内仅进行单项LID设施的布局无法达到最佳的雨洪调控效果,若考虑最大化提升城市雨洪的调控能力,决策者应进行组合LID设施的建设布局。
3.4.2 组合LID设施优化结果分析 组合LID设施建设布局也需要进行优化求解,对组合LID设施的优化解集同样按建设成本由小到大选取3种方案进行优化效果分析。对于图6(c)中组合LID设施的优化解集,选取方案1的建设成本和峰值积水削减量分别为23 800 000元、923.6 m3;选取方案2的建设成本和峰值积水削减量分别为62 160 000元、1 082 m3;选取方案3的建设成本和峰值积水削减量分别为102 100 000元、3 391 m3。将组合LID设施建设成本由低到高进行建设效果分析,各方案的优化解效果对比见图8。
由图8可以看出,3种方案对城市雨洪的调控效果与单项LID设施的调控效果变化趋势较为一致,均呈现出随建设成本增加峰值积水削减量也相应增加的规律。然而,根据图6(c)所示的组合优化解集,随着组合LID设施建设成本的增加,研究区域峰值积水削减量先缓慢增加,至成本达到62 160 000元后,峰值积水削减量急速增加。主要原因为,组合LID设施在低成本建设条件下,透水铺装与雨水花园协同建设的成本虽然在急剧增加,但由于此类低成本LID方案在全区域的覆盖率仍然较小,仅按前文2.3节的方法优先考虑了积水较为严重或地籍属性较为重要的重点区域,此时全区域的雨洪调控能力达不到理想的效果,导致了组合LID设施在低成本建设条件下雨洪调控效果较同成本的单项LID措施效果更差。
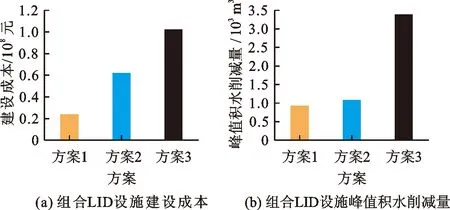
图8 组合LID设施优化结果对比分析
根据图6中的优化解集,选取同一建设成本方案对单项及组合LID设施雨洪调控效果进行对比分析,如图9所示。同为0.315×108元建设成本的优化方案下,得到透水铺装的峰值积水削减量为2 226.70 m3,雨水花园的峰值积水削减量为601.81 m3,组合LID设施的峰值积水削减量为944.49 m3。造成组合LID设施雨洪调控效果低于单项LID措施的主要原因在于LID设施的建设面积,在此种成本建设方案中,组合LID与单项LID设施的建设成本虽然相同,但组合LID设施方案中透水铺装的建设面积为2 429.6 m2,雨水花园的建设面积为61 771.0 m2。而由图9及表3可知,在单项LID设施中,相同建设面积条件下,透水铺装的雨洪调控效果是大于雨水花园的。在同一建设成本方案中,组合LID设施由于需要兼顾两个单项LID设施,从而削弱了较优效果LID设施的建设面积权重,由此出现同一建设成本方案中组合LID设施建设方案的雨洪调控效果比某些单项LID设施雨洪调控效果更弱的情况。但随着建设成本的逐渐增加,组合LID设施建设面积中各单项部分的建设面积也随之增加,就会使得组合LID设施的雨洪调控效果超过任意单项LID设施。因此,组合LID设施相对于单项LID措施具有低成本低效果、高成本高效果的特性。

图9 相同建设成本单项及组合LID设施优化效果对比
4 讨 论
将本文的LID设施优化设计方法应用于所选研究区域的海绵城市建设,雨洪调控规律为:随着LID设施建设面积的逐渐增加,雨洪调控效果也在逐渐增强,与周昕等[16]的研究结果相符。由此可见,建设LID设施对城市雨洪有着明显的削减效果[7,22]。为得到成本-效益最佳的优化方案,采用NSGA-Ⅱ算法对各类LID设施建设方案进行效益寻优,得到了单项及组合LID设施的优化解集,解集规律与相关学者的研究结果一致[17-18],表明耦合NSGA-Ⅱ算法与高精度水动力模型的LID设施优化设计方法切实有效。该方法通过高精度水动力模型驱动评价各类工况下LID设施的建设效果,相较于水文模型的评价方法,对地表的产汇流过程表达更为准确,因此总体的优化结果也更为精准,为以后的海绵城市建设提供了新思路。但由于缺乏基础调研资料,无法更明确地对比该方法与其他学者设计方法的优化解的精准程度,仅从雨洪评价模型的原理上进行了定性分析,下一步研究可以对研究区域基础资料进行深化调研,进一步研究该方法的优化效能。
5 结 论
基于NSGA-Ⅱ算法并利用高精度耦合水动力模型提出了一种新型LID设施优化设计方法,该方法以高精度水动力数值模型计算结果中的峰值积水削减量表征LID设施的建设效果,通过拟合LID设施建设面积与建设效果关系的经验公式,用NSGA-Ⅱ算法得到了LID设施优化设计的Pareto优化解集。并将该方法应用于西咸新区海绵城市建设,得到了以下结论:
(1)不同成本下两种单项及其组合LID设施的建设效果表明,单项及组合LID设施建设的雨洪调控效果均呈现出随着建设成本的增大,建设效果也随之增加的趋势。
(2)同一低成本建设方案下,由于组合LID设施方案中拥有较优渗水能力的单项LID设施比重较小,会出现组合LID设施建设效果低于某个单项LID设施建设效果的情况,但随着建设成本的持续增加,组合LID设施的雨洪调控效果会优于单项LID设施。
实例计算分析所得出的结论与实际相符,说明了该方法对于LID设施优化设计的自动寻优具有较高的准确性。该方法的建立,旨在通过高精度水动力模型完善传统水文模型模拟计算中的不足,达到提升LID设施优化设计结果准确性的目的,以期为未来的城市LID设施建设提供更加可行的设计方案,从而进一步推动城市海绵化进程,提升城市水环境质量。
