基于遗传算法优化BP神经网络的岩溶泉水位预测研究

陈奂良， 李常锁， 高 帅， 孙 斌， 林广奇

(1.山东省地质矿产勘查开发局 八〇一水文地质工程地质大队， 山东 济南 250014； 2.山东省地下水环境保护与修复工程技术研究中心， 山东 济南 250014； 3.山东省地质矿产勘查开发局 地下水资源与环境重点实验室， 山东 济南 250014)

1 研究背景

我国北方岩溶水资源不仅是城市生活及工农业生产的重要供水水源，其独特的岩溶泉更是珍贵的自然、文化遗产和旅游资源[1]。山东省鲁中南地区碳酸盐岩地层广泛分布，由于其特殊的水文地质条件而形成大量的岩溶大泉景观[2]，其中以“泉城”济南市的趵突泉、黑虎泉、珍珠泉、五龙潭四大泉群最为出名[3]。随着城市经济社会的快速发展，城市面积不断扩张，城市需水量持续增加，人为地改变了岩溶水的自然循环条件。20世纪70年代，济南市区内各泉群开始出现断流现象，随后当地政府采取了封停敏感区自备井、进行生态补源等泉水保护措施，取得了良好的效果，2003年，济南市区四大泉群相继复涌[4]。目前，以泉水位为调控目标的生态补源已经成为济南市泉水保护的重要措施之一，但由于岩溶水系统含水介质各向异性、不均质性，泉水位动态响应具有明显的滞后性，这就导致生态补源效果的滞后性，可能会导致泉水位低于最低警戒线。因此，如何实现岩溶泉水位动态的准确超前预测是优化生态补源方案的重要依据。

岩溶泉水位监测、预警问题一直是岩溶水资源开发、保护工程的重点和难点，常用的预测方法有数值法[5-6]、灰色系统预测法[7-8]、神经网络预测法[9-10]等，每种方法具有其特有的适用性。数值法是采用GMS、MODFLOW、FEFLOW等建模软件，结合地质、水文地质、钻孔资料构建水文地质模型，再依据已有气象、水文等资料建立水流模型，经过不断识别、验证来得到合理的地下水流动规律，最后通过修改环境变量对岩溶泉水位、水量进行预测的一种方法，该方法具有可视化、形象具体的特点。灰色系统预测法是利用少量、不完全信息建立数学模型的一种预测方法，它需要对原始数据进行生成处理，获得规律性强的数据集，然后建立微分方程模型对事物未来发展趋势进行预测，具有所需信息量少、运行方便等特点。人工神经网络是一种通过模拟生物神经网络结构而形成的计算模型，它通过具有多层、多节点的神经网络模型的自我学习过程，不断调整内部节点之间的连接关系，达到不断逼近目标输出的目的，具有自学习、自适应等特点。由于岩溶水系统的水文地质条件非常复杂，同时存在自然、人为双重控制因素，岩溶泉水位与其影响因素具有高度非线性关系，因此，能够实现高度非线性映射的人工神经网络预测方法是进行岩溶泉水位预测的常用方法。

研究区趵突泉泉域是我国北方较为典型的岩溶水系统，国内外学者采用水化学、同位素、野外示踪试验等手段对趵突泉泉域水循环过程、水动力条件、水化学条件等开展了大量研究。趵突泉泉域水循环研究表明，该泉域岩溶水补给来源主要为大气降水[11]，大气降水进入含水层后沿优势渗流通道向排泄区径流[12-16]，与此同时岩溶水不断与围岩发生溶滤作用、混合作用等水文地球化学演化过程[17-19]。岩溶水动力条件受大气降水、人工开采等多种条件影响，部分学者采用小波分析、线性回归等方法定量评价地下水位与降水的动态关系[20-21]，利用Mann-Kendall法、Hurst指数法分析了泉域岩溶泉水位动态变化的趋势性、蠕变性和持续性[22]等，以上研究大大提高了趵突泉泉域岩溶地下水位动态变化特征的研究精度。但在自然环境、人类活动的双重影响下，趵突泉泉域内岩溶大泉曾一度断流，当地采取禁采、限采、玉符河人工生态补源等措施后，区内岩溶大泉得以复涌。而目前人工生态补源工程的补源量和补源时间仅依靠泉水水位变化趋势进行定性判定，缺乏对泉水水位变化趋势的精确预测，无法实现人工生态补源措施的可预见性和超前性。

因此，本文在前人的研究基础上，采用大气降水、人工开采量、补源量等影响因素作为模型输入，以趵突泉水位为模型输出，构建了BP神经网络、基于遗传算法优化的BP神经网络(GA-BP神经网络)等多种预测模型，评价了不同预测模型对趵突泉水位的预测效果，确定了趵突泉水位动态预测的最优模型，可为人工生态补源工程的设计、实施等提供参考依据。

2 材料和方法

2.1 研究区概况

济南市趵突泉位于趵突泉泉域的北部排泄区，地势东南高西北低，南部、东南部为中低山地貌，中部多为低山丘陵地貌，北部、西部为微倾斜平原地貌，标高从南部的600～700 m(灵岩山683.7 m)降到中部的100～300 m(千佛山274.0 m)，再降至北部的25～50 m(趵突泉26.3 m)。研究区属温带大陆性气候，多年平均气温为14.2 ℃，多年平均降雨量为646.55 mm，6-9月为丰水期，12-次年5月为枯水期，多年平均蒸发量为1 500～1 900 mm。

研究区位于华北地层鲁西地层分区北部，受燕山期、喜山期等多期构造运动控制，南部基底抬升，形成由南向北倾斜的单斜构造[4]。南部出露新太古届泰山群基底层，岩性以片麻岩、闪长岩为主；中南部为古生代寒武系、奥陶系地层，岩性以灰岩、白云质灰岩、白云岩为主；北部覆盖新近系、第四系地层，岩性以砂质黏土、黏质砂土为主。区内地下水类型以裂隙岩溶水为主，寒武系中统张夏组、上统炒米店组及奥陶系下统三山子组为主要裂隙岩溶含水层，受地质构造、地形地貌控制，区内碳酸盐岩地层垂向、水平向的溶隙、溶孔发育良好，连通性好，有利于地下水的补给、径流和富集[23]。趵突泉泉域地质构造及泉群分布如图1所示。

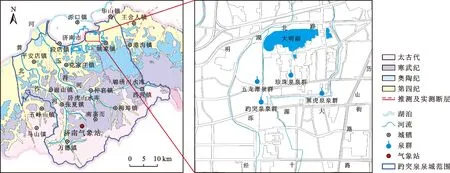
图1 趵突泉泉域地质构造及泉群分布图

在研究区南部的广大低山丘陵区，碳酸盐岩地层垂向裂隙发育，大气降水可直接或通过岩溶干谷垂直入渗，另外，玉符河、北沙河等地表水体的垂直渗漏补给也是岩溶水系统重要的补给来源。受地形坡向、地层倾向的控制，岩溶水由东南向西北径流，径流至市区附近时受侵入岩体的阻挡，岩溶水在岩体附近呈东西条带状富集，岩溶水头的升高使一部分岩溶水在地势低洼处涌出地面，以泉的形式排泄，另一部分沿地层向深部、北部径流[24-25]。研究区岩溶地下水的人工开采包括水源地开采、农业灌溉及自备井开采。由于泉水保护的需要，研究区内水源地大多已停止开采，仅有少数水源地保持较低开采量，每年主要有3次规模较大的农业灌溉，分别是每年的3、6、10月份，另外区内还存在少量工业自备井开采岩溶水。区内生态补源工程措施以河流、湖泊等强渗漏区域自然渗漏补源为主，主要选取泉域内玉符河、兴济河、历阳湖、小岭等区域开展生态补源，补源水主要来源于水库截留、南水北调工程或大明湖弃水等。相关部门可根据泉水水位、降水量等情况，适时调整生态补源位置、时段、补源量，由于每年降水情况不同，对泉水水位预期不同，生态补源量也相差较大。

2.2 数据来源及预处理

本文利用2016年1月1日至2018年12月31日每日降水量、岩溶水开采量、两处生态补源量、趵突泉水位日监测数据开展研究。其中，济南地区降水量数据来源于国家气象科学数据中心(http://data.cma.cn/)济南站降水数据，数据已经过均一性检验及质量控制，其他数据来源于山东省地矿局八〇一水文地质工程地质大队长期保泉工作收集、监测的数据，均由专业人员进行收集和监测，确保数据真实有效。

根据当地水文地质条件，降雨量、开采量、补源量是影响趵突泉水位动态变化的主要因素，而且这些因素的影响效果具有滞后性，另外随着预见期的增加，预测精度也会随之下降[10]，因此本文选择预见期为1 d，即将岩溶水开采量、两处生态补源量及前3 d、前2 d、前1 d的降水量等6个影响因素作为模型输入，当日趵突泉水位作为模型输出。

为了有效评价模型预测的准确性，将数据样本分为训练样本和测试样本，其中选取2016年1月1日至2017年12月31日时段的数据作为训练样本，2018年1月1日至2018年12月31日时段的数据作为测试样本，训练样本和测试样本各参数的统计结果见表1。由表1可以看出，测试样本大部分参数的分布范围在训练样本各参数的分布范围内，有利于提高模型的鲁棒性。

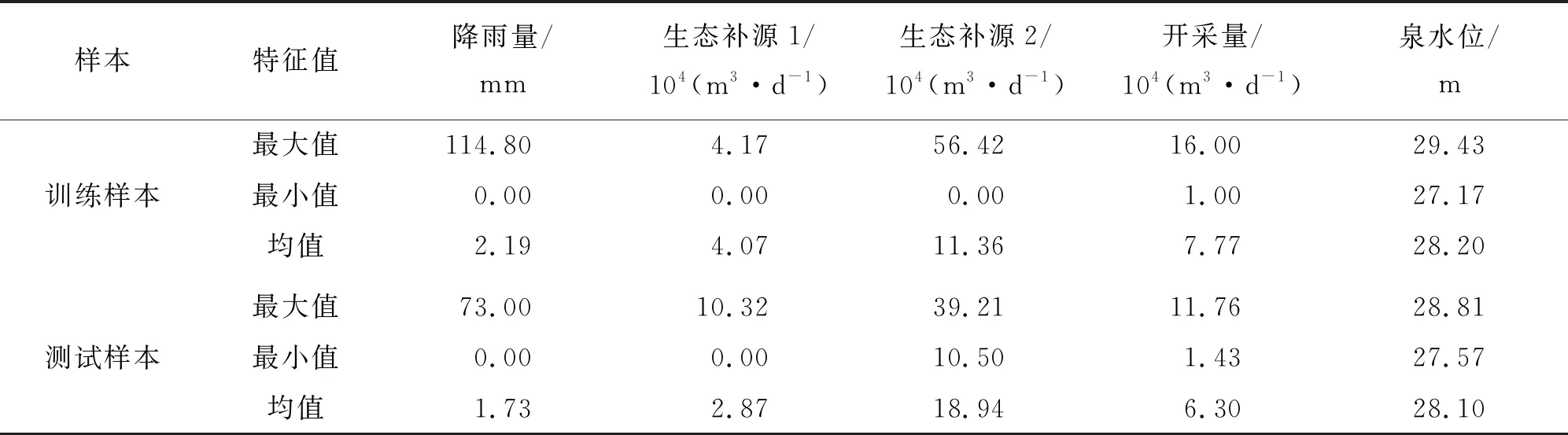
表1 训练样本和测试样本各参数统计表

另外，为了尽可能地减小训练误差，加快模型训练的收敛速度，在模型训练前将数据归一化到[-1,1]区间：

(1)

2.3 BP神经网络算法

人工神经网络是一种通过模拟生物神经网络结构而产生的计算模型，能够进行高度非线性映射，具有一定的稳定性和容错性[26]。在众多神经网络模型中应用最为广泛的是前馈BP(back propagation)神经网络模型，它是一种运用误差反向传播算法训练的多层前馈神经网络，其模型结构由一个输入层、一个输出层及一个或多个隐含层构成。以本文研究内容为例介绍BP神经网络的训练过程。在预测过程中，首先以岩溶水开采量、两处生态补源量及前3 d、前2 d、前1 d的降水量等6个影响因素作为输入层的6个节点，每组数据输入后进入隐含层，每个隐含层节点对各个输入数据进行有权重的线性叠加并加上阈值，得到的结果作为隐含层节点的输入，再将隐含层节点的输入代入传递函数得到隐含层节点的输出，以此计算得到所有隐含层节点的输出。以同样的方法计算得到输出层的输出结果，即本次计算预测的趵突泉水位(输出层1个节点)，再采用性能函数评估预测水位与实测水位，若不在设定的误差允许范围内，则信号逆向反馈，通过学习函数调整网络各层的权值、阈值后重新计算。如此反复迭代，直到误差进入目标误差范围或达到最大迭代次数[10]，得到趵突泉水位的神经网络预测模型，再利用已有输入数据进行水位预测。

隐含层数量一般采用经验公式(2)确定[27]，根据公式计算可以得到隐含层数量在5～14之间，再采用逐个尝试比较相对误差的办法，最终确定隐含层数量为11，网络结构如图2所示。

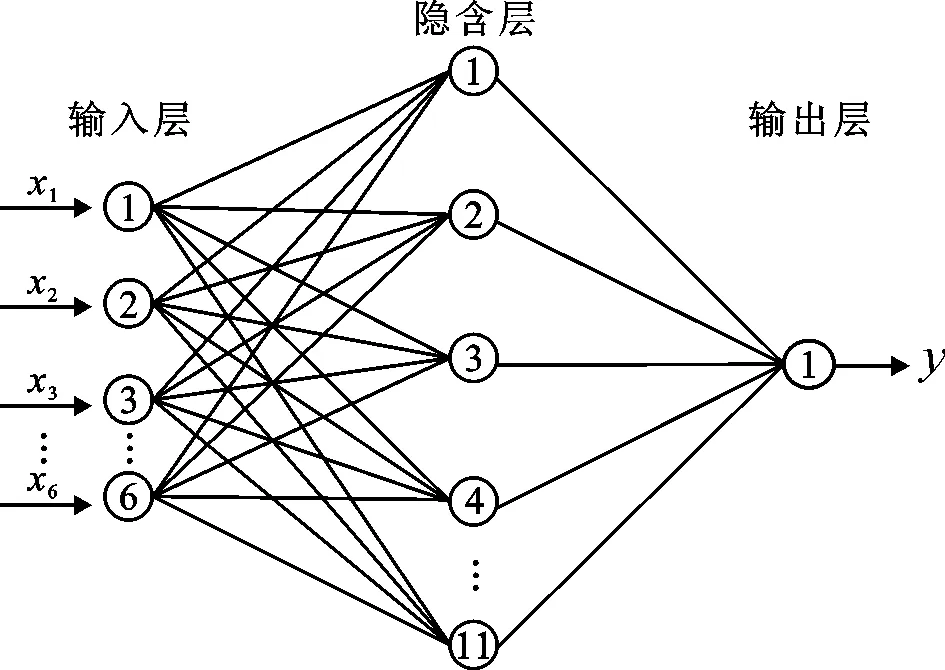
图2 本文采用的神经网络结构

(2)

式中：P为隐含层节点数量；n为输入层节点数量；m为输出层节点数量；a为1～10间的整数。

本文选取S型函数Sigmoid函数作为神经网络中各层间的信号传递函数，将信号非线性映射到(0,1)区间内。

f(x)=1/(1+e-x)

(3)

隐含层神经元和输出层神经元的输入、输出表达式为：

(4)

Oj=f(Ij)=1/(1+e-Ij)

(5)

式中：Ij为隐含层或输出层第j个神经元的输入；wij为从上一层第i个神经元输出到隐含层或输出层第j个神经元的权重；θj为隐含层或输出层第j个神经元的阈值；Oj为隐含层或输出层第j个神经元的输出；f(x)为传递函数；n为上一层神经元的数量。

神经网络中常用的性能函数为均方误差(mean square error，MSE)函数，通过比较模型输出与真实值误差平方和的平均值与目标误差进行比较，判断下一步计算过程。

(6)

若模型输出不符合预期，BP神经网络会在误差反馈过程中对权值、阈值进行调整，实现对各神经元计算结构的调整，逐渐逼近期望输出。在误差修正环节，权值常采用梯度下降法确定，以隐含层与输出层权重修正过程为例，具体数学表达式如下：

(7)

wjk(n+1)=wjk(n)+Δwjk(n+1)

(8)

式中：η为学习因子；E为误差；Δwjk(n+1)为权重修正值；wjk(n)、wjk(n+1)分别为更新前和更新后的权重。阈值的更新理论与权重类似，逐层向前调整权重和阈值矩阵。

2.4 遗传算法

遗传算法(genetic algorithm，GA)是Holland教授结合Darwin的进化论和Mendel的遗传学思想提出的解决寻优问题的一种算法，其具有较好的自适应和寻优能力[28]，而BP神经网络的收敛速度、精确度受初始权重和阈值的影响。因此，为了避免传统BP神经网络受随机初始权重和阈值影响而陷入局部最优，并提高收敛速度和节省计算成本，本文采用GA算法优化BP神经网络模型的初始权重和阈值，其优化流程如图3所示。

图3 GA算法优化BP神经网络模型的流程

首先基于BP神经网络初始权重和阈值结构，随机产生一组权重和阈值组合(染色体)，多个染色体组成一个种群，整个种群中的染色体分别通过网络进行运行计算后，得到各个染色体的适应度值，根据适应度值进行选择、交叉及变异操作，得到新的染色体种群，再次评估适应度值，不断迭代直至达到目标要求[29-30]。

本文采用的遗传算法选择预测输出与期望输出的绝对差作为各个染色体的适应度值，用于表征染色体的优劣性。遗传算法的选择操作可以由多种方法实现，例如锦标赛法、轮盘赌法、最佳个体保存法等，本文选择常用的轮盘赌法在已知每个个体适应度值的基础上进行选择。交叉操作是选取两个染色体，对染色体中一点或多点的位置进行交换，从而产生新的染色体，体现自然界信息交换思想，交叉概率一般为0.20～0.99，本文设置交叉概率为0.7。变异操作是以一定概率选择变异的染色体，将被选染色体某个基因进行变异，一般变异概率为0.0001～0.2，本文设置变异概率为0.1。经多次调试发现，遗传算法迭代20次后权值和阈值组合的适应度值趋于平稳，为了节省计算成本，将遗传算法的终止迭代次数设为20。

对于BP神经网络模型而言，不同的训练算法导致其目标误差及收敛速度也不同，因此为了得到最优的预测模型，本文进行3种训练方法，即梯度下降法(traingd)、有动量的梯度下降法(traingdm)和Levenberg-Marquardt法(trainlm)对BP神经网络模型、GA-BP神经网络模型等6种模型进行训练并评价训练效果，选择最佳的神经网络模型开展泉水位预测分析。

2.5 评价指标

为了全面评价各个模型预测结果的准确性，采用均方根误差(root mean square error,RMSE)、纳什效率系数(Nash-Sutcliffe efficiency coefficient，NSE)和平均绝对误差(mean absolute error,MAE)来对比分析各个模型的表现能力，各指标具体计算公式如下：

(9)

(10)

(11)

3 结果与分析

3.1 模型预测效果评价

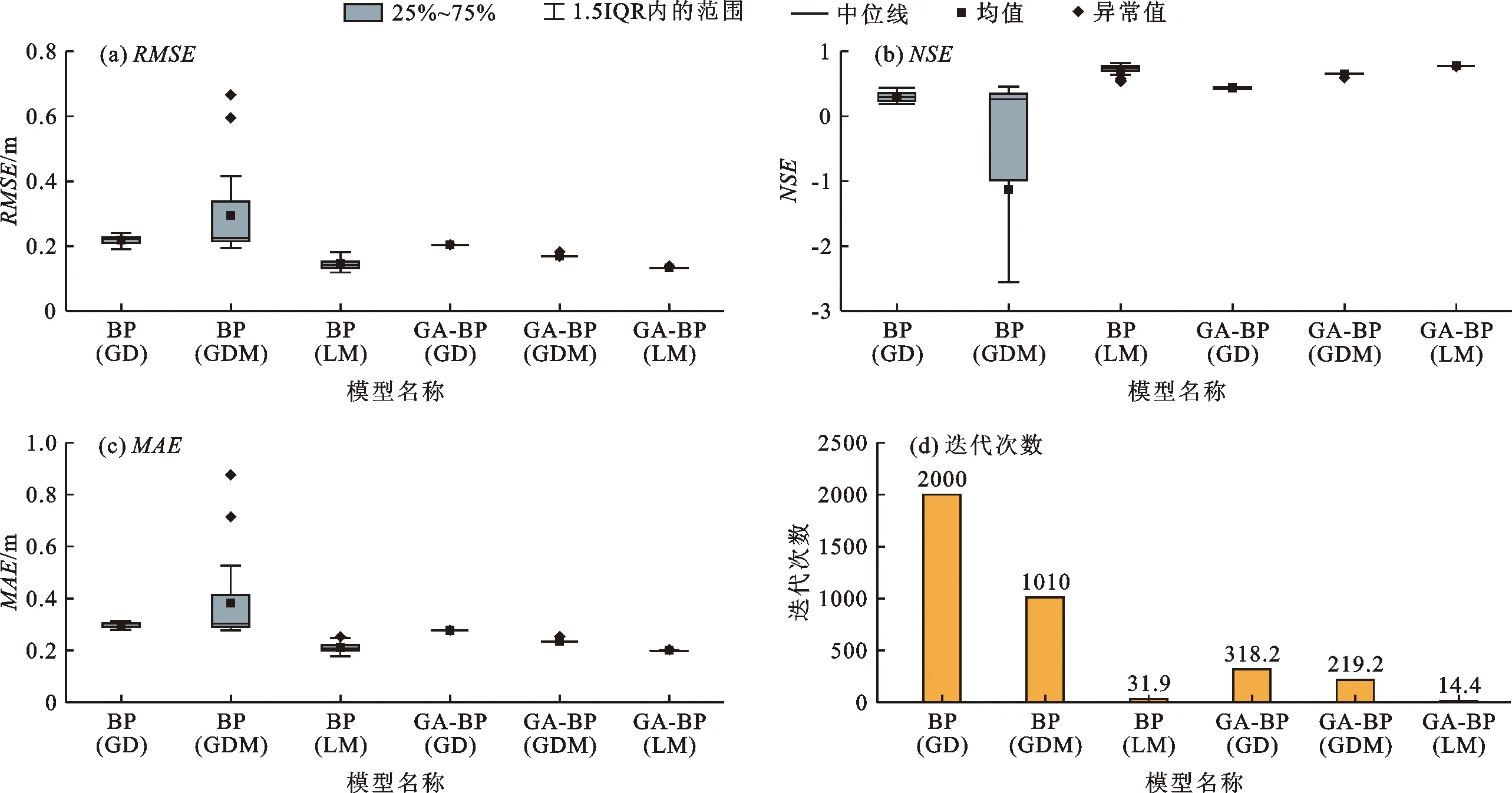
若神经网络模型的权重和阈值的赋值方式、训练函数不同，则其预测效果也不尽相同。为了更真实地反映不同模型预测效果的差异，本文对每种模型分别训练20次，对每次预测计算得到的RMSE、NSE、MAE及总迭代次数4个评价指标进行统计分析，对比模型间的预测效果。

不同模型预测结果的各评价指标及迭代次数统计分析见图4。由图4可以看出，BP神经网络模型与GA-BP神经网络模型的预测结果评价指标整体差异较大，不同训练方法的BP神经网络模型的预测结果评价指标RMSE、NSE、MAE也表现出较大的变异性，说明权值和阈值采用随机赋值的方式会增大模型预测的不稳定性及偶然性。而GA-BP神经网络模型的3个评价指标的变异性极小，且RMSE、MAE值略小于BP神经网络模型，NSE值略高于BP神经网络模型，说明采用GA算法优化得到的权值和阈值作为BP神经网络模型的初始值可以有效提高模型预测的稳定性，且对预测效果也有一定的改善。另外，在相同目标误差的情况下，GA-BP神经网络模型的迭代次数明显少于BP神经网络模型，表明GA算法可以大大减小BP神经网络模型运算的迭代次数，节省大量计算成本。

进一步对比图4中不同训练方法之间的差异可以看出，无论是BP神经网络模型还是GA-BP神经网络模型，以Levenberg-Marquardt法训练的模型预测结果评价指标RMSE、MAE值均为最小，而NSE值的排序为梯度下降法<有动量的梯度下降法

3.2 GA-BP(LM)模型预测效果

模型的预测误差或其百分比是评价模型是否能够实际应用的重要参数。因此，为了进一步分析模型的预测效果，分别计算了6种神经网络模型的训练阶段(2016年1月1日至2017年12月31日)和预测阶段(2018年1月1日至2018年12月31日)的预测误差分布并统计了其误差特征值，结果见图5和表2。

注：神经网络模型名称中的(GD)、(GDM)和(LM)分别表示训练方法为梯度下降法、有动量的梯度下降法和Levenberg-Marquardt法图4 不同模型预测结果的各评价指标及迭代次数统计分析

分析图5和表2可知：(1)BP(GD)、BP(GDM)、BP(LM)模型的误差在训练阶段和预测阶段均较大，特别是在预测阶段误差增大，误差变异系数分别为0.32、0.30、0.29，说明模型预测结果的稳定性较差，且不能很好地表征趵突泉水位动态变化的物理机制。(2)GA-BP(GD)、GA-BP(GDM)模型虽然能够很好地拟合数据，但是在预测阶段误差陡增，误差变异系数分别为0.37和0.59，不能很好地预测趵突泉水位真实的动态变化过程。(3)GA-BP(LM)模型的预测误差较小，误差值基本在0值附近小幅度波动，变化趋势稳定，误差变异系数为0.13，其预测结果的精度及稳定性明显优于其他模型，表明该模型能够很好地表征降水量、开采量、补源量对趵突泉水位动态变化的影响机制。(4)BP(GD)、BP(GDM)、BP(LM)模型与GA-BP(LM)模型的误差分布范围和平均值均相差不大，但GA-BP(LM)模型的误差标准差明显小于前三者(表2)，表明GA-BP(LM)模型的预测误差基本围绕平均值小幅度波动，能够稳定、准确地预测泉水位的动态变化过程。

图5 6种神经网络模型训练阶段和预测阶段的预测误差分布

表2 6种神经网络模型的预测误差特征值统计

本文的研究目标是实现济南市岩溶大泉水位的准确预测，基于上述分析，选取GA-BP(LM)模型进行趵突泉水位预测分析。将2018年的测试样本数据输入到训练好的神经网络模型中得到预测水位输出值，预测水位与实际观测水位动态变化曲线对比见图6。由图6可以看出，该模型的训练数据和预测数据均能够很好地拟合实际观测泉水位曲线，预测阶段NSE值达到0.84，表明GA-BP(LM)模型对泉水位动态变化具有较高的预测精度。

图6 GA-BP(LM)模型预测水位与实际观测水位动态变化曲线对比

4 结 论

北方岩溶泉水位动态变化是受自然和人为因素共同影响的高度非线性变化过程，其变化特点不仅具有趋势性，还具有一定的随机性。基于岩溶泉水位动态变化特征，本文提出采用神经网络算法进行岩溶泉水位的预测研究，得到以下结论：

(1)GA-BP神经网络性能明显优于传统BP神经网络。由于BP神经网络存在易陷入局部最优解的缺陷，采用BP神经网络进行泉水位预测会产生预测结果不稳定、计算成本高的问题。而经过GA算法优化后的BP神经网络模型可以避免陷入局部最优解，保证了预测结果的稳定性并降低了计算成本。

(2)GA-BP(LM)模型更适用于泉水位的预测。神经网络模型的学习算法对预测的稳定性和准确性有较大影响，在梯度下降法、有动量的梯度下降法和Levenberg-Marquardt法3种训练方法中，基于LM法的GA-BP神经网络模型具有稳定性高、计算成本低、预测误差小的特点，更适合对高度非线性的岩溶泉水位动态变化过程进行预测。

受训练样本量相对较少、样本采样空间权重统一、随机因素不确定等因素的影响，神经网络模型在趵突泉水位预测中存在一定的误差，今后可在利用实采时监测传输的降水量、开采量及补源量等数据实现模型的滚动修正预测，根据地下水系统理论判断各岩溶水开采点和补源点对泉水位动态变化的影响权重关系，确定随机因素及其概率分布特征等方面继续完善预测模型，以进一步提高岩溶泉水位的预测精度。