基于UKF的磁流变阻尼器模型更新混合试验方法

孟丽岩， 李 勐， 陈鹏帆

(黑龙江科技大学 建筑工程学院， 哈尔滨 150022)

0 引 言

混合试验是一种结合物理子结构试验加载和数值模拟技术的试验手段，可以有效评价结构的地震响应，在土木工程领域得到了广泛的应用。Hakuno[1]最早提出混合试验的概念，将结构中重要的部分作为物理子结构进行试验加载，数值子结构假定有可靠的模型在计算机中模拟。近年来，混合试验已在数值积分算法、时滞补偿及模型更新等关键方面取得了很大进展[2-5]。

混合试验的数值部分建模是否准确，将影响混合试验精度，模型更新是解决这一问题的有效手段。Yang[6]首次将模型更新方法应用到混合试验中，采用神经网络算法对数值子结构的参数进行识别，利用事先训练好的神经网络预测数值子结构的恢复力，降低数值子结构模型误差对试验结果的影响。王涛[7]提出UKF模型更新混合试验方法，通过试验验证该方法较传统混合试验方法更具有鲁棒性。梅竹[8-9]提出一种在不同边界条件下的模型更新混合试验方法，对钢筋混凝土悬臂柱进行数值仿真，得出UKF能够在线识别材料本构模型参数，同时更新应用相同材料的结构的本构模型参数。陈再现[10]提出基于均匀设计的模型更新混合模拟方法，在试验子结构的基础上，通过均匀设计方法构造验算子结构样本空间，得到最符合试验子结构的数值模型用于模型参数更新，有效提升了识别效率。

鉴于此，笔者提出基于UKF的磁流变阻尼器在线模型更新数值仿真方法，以磁流变阻尼器的Bouc-Wen模型为研究对象，研究Bouc-Wen模型参数对滞回曲线的影响，给出Bouc-Wen模型参数的合理取值建议，数值仿真磁流变阻尼器在线模型更新，识别模型参数，通过与传统混合试验对比，验证所提方法的有效性。

1 磁流变阻尼器的Bouc-Wen模型

1.1 Bouc-Wen模型

1976年，Wen[11]提出磁流变阻尼器的Bouc-Wen模型。该模型的结构原理如图1所示。

由图1可见，Bouc-Wen模型的表达式为

(1)

式中：z——滞回位移，m；

x——位移，m；

x0——初始位移，m；

F——恢复力，kN；

c0——阻尼系数，kN·s/m；

k0——刚度，kN/m；

A、β、γ、α、n——滞回环形状的参数。

1.2 Bouc-Wen模型参数对滞回曲线的影响

Bouc-Wen模型能较为准确反映磁流变阻尼器的应力-应变关系，具有较高的精度，简单方便，易于程序化。为保证在后续模型参数识别过程中，参数调节的有效性，分析磁流变阻尼器的Bouc-Wen模型参数对滞回曲线的影响。n、β和γ的边界可以通过Ismail[12]的热力学分析获得。其中，n、β大于0且-γ≤β≤γ，另外，k0>0，α>0。

1.2.1 黏滞阻尼系数

参数c0代表黏滞阻尼系数，通常与速度的大小有关，反映了力-速度曲线的平均斜率，黏滞阻尼系数c0的具体表达式为

所有参数取值如表1所示。令c0取三组不同的值，分别为40、100、10 kN·s/m。观察c0对磁流变阻尼器的滞回曲线的影响，如图2所示。

表1 模型参数取值

由图2可知，c0对滞回曲线的影响很小。滞回曲线的形状主要与速度有关，在一定范围内几乎不改变位移-恢复力滞回曲线形状。

1.2.2 刚度

参数k0代表模型刚度，通常与位移大小相关，反映了力-位移曲线的平均斜率，刚度k0的具体表达式为

令k0取三组不同的值，分别为30、50、100 kN/m。其余参数如表1所示。观察k0对磁流变阻尼器的滞回曲线的影响，如图3所示。

由图3可以看出，k0主要影响着滞回曲线的恢复力位移曲线斜率，对整个滞回曲线的形状几乎无影响。

1.2.3 屈服刚度差值

参数α代表前屈服刚度与后屈服刚度的差值k1-k2，主要反映了力-速度曲线由线性到非线性的变化率的大小。参数α通常与滞回变量z有关，而z在磁流变阻尼器的Bouc-Wen模型中属于中间变量，影响因素众多，因此，确定α的取值比较困难，一般根据经验，由位移的大小确定α的取值，屈服刚度差值 的具体表达式为

α≤1.5(xmax-xmin)。

令α取三组不同的值，分别为900、100、500 kN/m。其余参数如表1所示。观察α对磁流变阻尼器的滞回曲线的影响，如图4所示。

由图4可知，α取值的不同明显改变了磁流变阻尼器滞回曲线的形状。由于参数α与滞回变量z相关，因此，对恢复力的影响较为显著。

1.2.4 尖锐系数

尖锐系数n控制着滞回环的尖锐程度。令n取三组不同的值，分别为2、1、3。观察n对磁流变阻尼器的滞回曲线的影响，如图5所示。

由图5可以看出，n值改变了滞回曲线的形状且主要影响的是滞回曲线的尖锐程度。

1.2.5 冗余参数

参数A、β、γ为控制滞回环大小和形状的参数，但是它们为冗余参数，没有明确的物理意义，作用是能够更好地控制各种不同激励下滞回曲线的形状。也就是同样的滞回环可以用不同的A、β、γ参数组合。因此，通常设A为110来确保其唯一性，其余参数如表1所示。由图6可以看出，除了β和γ，当所有的参数都相同时，Bouc-Wen模型的滞回曲线非常接近。

1.3 Bouc-Wen模型参数敏感性

为研究磁流变阻尼器Bouc-Wen模型参数的敏感度，采用OAAT法分别对试验1、2进行参数敏感性分析。模型输入为EI Centro地震波，地震加速度峰值为12.5 gal，磁流变阻尼器Bouc-Wen模型的各参数基值选择如下：

试验1α=880 kN/m，c0=50 kN·s/m，k0=25 kN/m，γ=100，β=100，n=2,A=207,x0=3.8 mm。

试验2α=900 kN/m，c0=40 kN·s/m，k0=30 kN/m，γ=110，β=90，n=2,A=110,x0=4 mm。

具体结果见图7和表2。由图7及表2可知，8个参数中α、A和n是最为敏感的，其他参数较为不敏感，并且不同的参数基点值的选取对于参数的敏感度有些微差别。这说明不同规格的磁流变阻尼器，不同的滞回系统，其模型的参数敏感性各有不同。在模型参数识别的调参过程中，所有的参数均是互相影响的，调节一个参数必然会对其余参数的识别算法的调节造成影响，这是一个繁复的过程。但是对于敏感性高的参数调参的幅度可适当减小，而敏感性低的参数调参幅度适当增加，这将大大增加识别算法参数的调参效率。

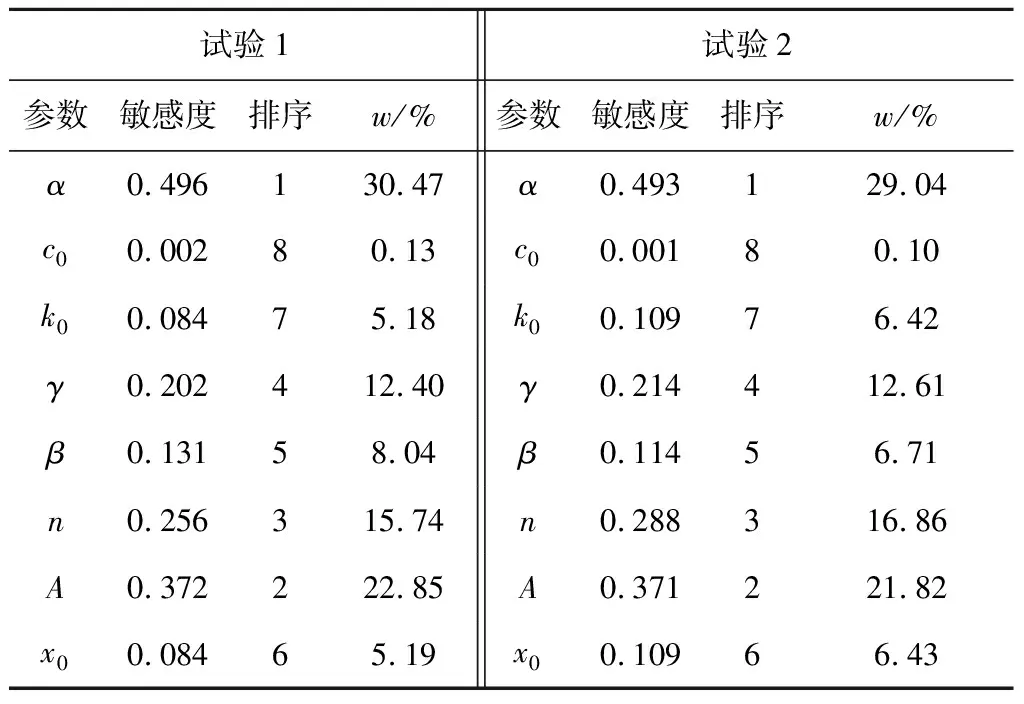
表2 敏感性分析结果

2 在线模型更新试验数值仿真

2.1 参数设置

在传统混合试验中，数值子结构的模型是事先假定的，不能保证其准确性。采用在线模型更新的方法能够在实时混合试验进程中不断改善数值子结构的模型，通过试验子结构的结构反应，使用参数识别算法识别出模型参数，然后将这些识别后的参数代替原有的数值子结构模型参数，从而更新数值子结构模型。基于此，将进行基于UKF的磁流变阻尼器在线模型更新混合试验数值仿真。为研究磁流变阻尼器的力学特性，考虑一个两层装有磁流变阻尼器的框架结构进行基于UKF的在线模型更新混合试验数值仿真，其中,第一层为试验子结构，第二层为数值子结构，如图8所示。

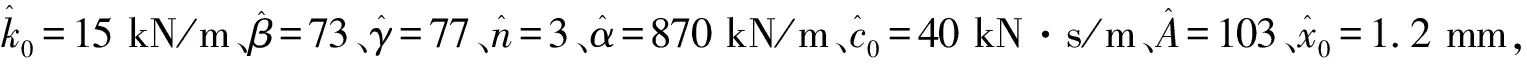
(2)

x3,k+1(uk+1-x4,k+1)+x5,k+1x1,k+1+wk+1。

(3)

初始协方差矩阵以及噪声矩阵的

P0=[10-410-310-410-410-410-410-510-4

10-510-2]×I10,

(4)

式中,I10——10×10的单位对角阵。

Q0=[10-80 0 0 0 0 0 0 0 10-8]T,

(5)

R=10-3×I10。

(6)

在试验过程中，每个积分步长内都需要实现两个模型的更新：一是在参数识别算法中完成模型更新，这是采用在线递推识别算法决定的；二是同时实时更新数值子结构模型，这也是模型更新混合试验中模型更新与传统模型更新的主要差别。

文中通过三种试验以验证基于UKF磁流变阻尼器的模型试验方法的有效性。假定数值子结构和试验子结构的力学模型一样，均选定为磁流变阻尼器的Bouc-Wen模型。三种类型的混合试验数值仿真中，试验子结构模型采用模型参数的真实值，以代表真实的物理试验。数值子结构模型参数的取值各不相同。

(1)真实混合试验模型参数采用真实值，其数值模拟结果代表真实试验的试验结果，在结果分析的图中用“Exat”表示。

(2)传统混合试验模型参数采用初始估计值。其数值模拟结果代表传统混合试验的试验结果，在结果分析的图中用“Conventional”表示。

(3)基于UKF的磁流变阻尼器在线模型更新数值模拟。模型参数将由UKF算法识别并在每个时间步中更新。其数值模拟结果代表文中提出的试验方法试验结果，在结果分析的图中用“UKF”表示。

2.2 结果分析

试验子结构和数值子结构的位移时程反应如图9所示，由图9可见，传统混合试验在第5 s时开始出现偏移，与真实值有所出入，且随着时间的增加并没有减弱的趋势。而采用基于UKF的在线实时更新混合试验数值仿真与真实混合试验的位移反应能够较好的吻合。

试验子结构与数值子结构的位移时程误差分析如表3所示。表中，x1max代表试验子结构的位移最大值，x1min代表试验子结构的位移最小值。x2max代表数值子结构的位移最大值，x2min代表数值子结构的位移最小值。从表3可以看出，传统混合试验不论是试验子结构还是数值子结构，最大值还是最小值的相对误差都远远的超过了基于UKF的磁流变阻尼器的模型更新混合试验的误差值。基于UKF的磁流变阻尼器的模型更新混合试验的相对误差很小，基本都在1%以内，较传统混合试验相对误差减小了97%以上。

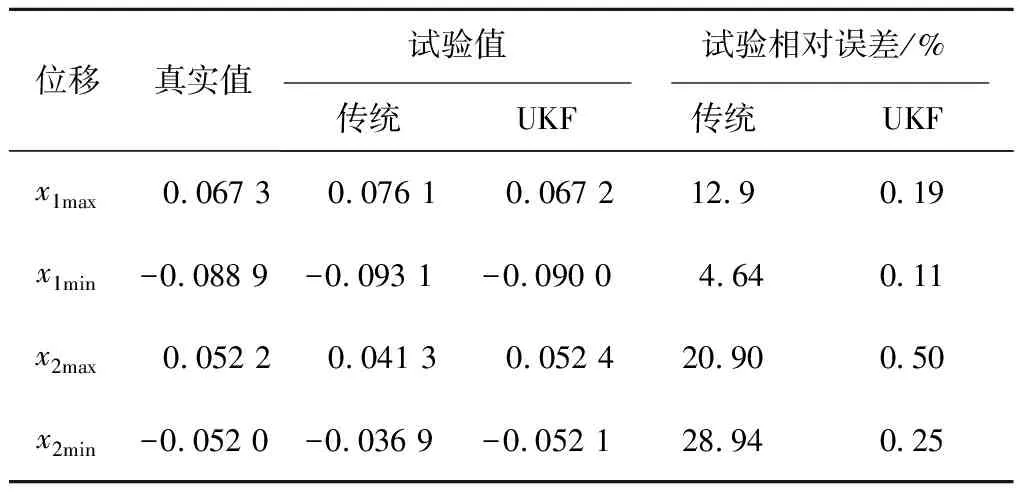
表3 位移时程曲线误差

试验子结构、数值子结构的滞回曲线如图10所示。可以观察到采用传统混合试验与真实混合试验的反应存在较大偏差，而采用基于UKF的在线实时更新混合试验与真实混合试验的位移反应能够吻合较好。这说明采用基于UKF的在线实时更新混合试验，通过试验子结构的反馈实时更新数值子结构的模型是十分有效的试验方法，对磁流变阻尼器的吻合非常好，误差明显减小，提高了混合试验精度。

磁流变阻尼器的恢复力模型参数的识别时程曲线如图11和12所示。采用基于UKF的在线实时更新混合试验能够在较短的时间内准确地识别出模型参数，也很快趋近于真实值。为了定量的观察识别的效果，表4给出了模型参数识别的误差分析。从表4可以看到，识别值与真实值的误差很小，进一步验证了文中提出的基于UKF的磁流变阻尼器在线模型更新混合试验的有效性。

式中：Ri——第i步的恢复力真实值；

Ri′——第i步采取的试验计算得到的恢复力；

M——迭代总步数。

传统混合试验的恢复力均方根误差RMSE为4.60×10-4，基于UKF方法得到的恢复力均方根误差RMSE为5.69×10-4。可以定量了解到，基于UKF的磁流变阻尼器在线模型更新混合试验数值仿真相较于传统混合试验较大提高了试验的精度。

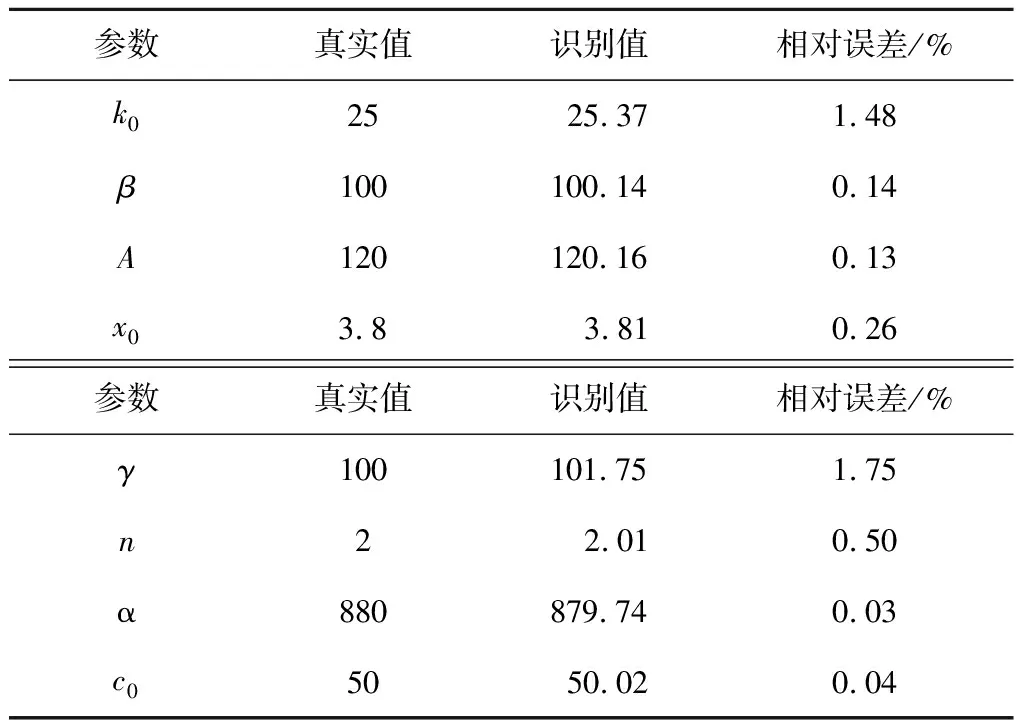
表4 参数识别曲线误差分析

磁流变阻尼器除了模型非线性的问题还需要面对实时加载的问题。由于磁流变阻尼器具有两个特性，一是模型非线性;二是加载实时性。对UKF的识别计算效率进行分析，如图13所示。识别时每步的用时基本在0.001 5 s左右，而地震记录每步的时间间隔也就是积分步长为0.01 s。文中采用的基于UKF的模型更新混合试验方法能够满足对磁流变阻尼器实时加载的要求。

基于UKF的磁流变阻尼器模型更新混合试验仿真耗时24.15 s，计算时间较短，可以用于快速在线实时更新混合试验。从图11～13可以看出，采用基于UKF的模型更新在线数值模拟方法得到的结果与结构真实反应基本吻合，较传统混合试验能够更大程度的反应出真实的结构反应。

3 结 论

(1)分析了磁流变阻尼器的Bouc-Wen模型参数的物理意义及其对滞回曲线的影响规律，可以得到8个参数中，α、A和n是最为敏感的，而其他参数较为不敏感，并且不同的参数基点值的选取对于参数的敏感度有些微差别，通过参数对滞回曲线的影响规律给出了算法初始参数预估值的合理取值建议。

(2)结果表明，相比传统混合试验方法，基于UKF的磁流变阻尼器模型更新混合试验数值仿真模型参数识别值及滞回曲线与真实值吻合程度较高，模型参数k0、β、A、x0、γ、n、α和c0相对误差分别为1.48%、0.14%、0.13%、0.26%、1.75%、0.5%、0.03%和0.04%，位移时程曲线均方根误差降低了11.55%，有效提高了模型更新混合试验数值仿真精度。证明该方法具有较好的精度和收敛速度且耗时较短，较传统混合试验有较大的改善。