基于RF-FR模型的滑坡易发性评价
——以略阳县为例
2022-08-29马啸王念秦李晓抗严冬李嘉琳
马啸,王念秦,李晓抗,严冬, 李嘉琳
(1.陕西工程勘察研究院有限公司,陕西 西安 710068;2.西安科技大学地质与环境学院,陕西 西安 710054;3.陕西乾和实业有限公司,陕西 西安 710000)
陕西是中国地质灾害最为严重的省份之一,据《陕西统计年鉴》:2012~2020年陕西省因地质灾害伤亡293人,而滑坡是造成人员伤亡最为主要的灾害类型之一。近年来,滑坡易发性评价已经成为滑坡灾害风险管控和监测预警的重要手段,众多科研人员致力于此项研究,并取得众多成果。
滑坡灾害易发性评价方法主要分为定性评价、半定量评价和定量评价3种类型。其中,定量评价是滑坡易发性区划最为主要的方法。随着GIS技术的快速发展,将其应用于滑坡灾害易发性评价领域将更加优化了定量评价的准确性。易发性区划评价方法主要有:层次分析法、信息量模型、频率比、逻辑回归、随机森林、支持向量机和人工神经网络等。目前,将2种或多种模型进行对比与耦合来进行滑坡易发性评价已成为国内外学者研究的热点。Chen Wei 等(2018)以太白县为例,将随机森林与确定性因子进行耦合,得出RF-CF模型,结果表明,该模型的精度优于单一的模型; J. Cao等(2019)采用逻辑回归和随机森林模型对川西山区的滑坡灾害易发性进行了评价,得出随机森林模型预测准确率高于逻辑回归模型。郭子正等(2020)基于加权频率比、逻辑回归和确定系数法,以万州区为例进行滑坡易发性评价,得出加权频率比的预测准确性更高。邱维蓉等(2020)通过LR、SVM、BP、RF 4种模型的对比与分析,得出RF模型优于其他3种模型。
结合前人研究得出:将随机森林(RF)模型应用于滑坡易发性评价具有较高的准确性与实用性,而频率比(FR)模型更加能反映滑坡的发育规律。因此,结合2种模型的优越性,将其进行耦合应用于滑坡易发性评价中可提高滑坡灾害易发性预测的准确性。笔者以略阳县域为研究区,首先将频率比(FR)、随机森林(RF)模型应用于滑坡灾害的易发性评价中,得出各模型县域滑坡易发性分区图及其准确性;其次以频率比替代各分级的评价因子数值,代入随机森林模型中进行2种方法的耦合,得出耦合模型下县域滑坡易发性分区图及其准确性。通过对比各模型准确性,得出研究结果。研究结果对滑坡易发性评价模型的优化具有借鉴意义,也可为相关部门进行滑坡防治提供理论依据。
1 研究区概况
略阳县位于陕西省汉中市西北部,地理坐标为东经105°42′~ 106°31′,北纬33°07′~33°38′。县域平面图略呈长方形,总面积为2 831 km2。属暖温带湿润季风气候,多年平均降雨量为860 mm,且降雨量分配不均,呈由西北向东南递增之势,多年平均气温为13.2℃。该区高程分布范围较广,为559~2 399 m,地势南北高、中间低。属于秦巴山区地貌类型。区内有嘉陵江和汉江2条水系,其中嘉陵江水系较大支流有10条,汉江水系较大支流有8条。区内构造断裂发育,主要有褒城断裂、茶店断裂、艾叶-官亭断裂、勉县-阳平关断裂。据统计,略阳县已发生地质灾害及隐患点共482处,其中,滑坡445处,占研究区内地质灾害总数92%。研究区地理位置及滑坡灾害点分布见图1。

图1 研究区地理位置及滑坡灾害点分布图Fig.1 Geographical location and landslide points distribution in research area
2 评价模型简介
2.1 随机森林模型
随机森林 (Random Forest Model,简称 RF) 是将多棵决策树进行集成的算法。随机森林算法能有效解决二分类问题,准确率高,使大数据、高维特征数据能够有效地运行,并且能够得到各评价因子的权重。其方法是:从数据集(N)中随机选择k个特征(列),共m个特征(其中k小于等于m);然后根据这k个特征建立决策树;重复n次,这k个特性经过不同随机组合建立起来n棵决策树,对每个决策树都传递随机变量来预测结果,得到高票数的预测目标作为随机森林算法的最终预测。
2.2 频率比模型
频率比模型(frequency ratio model,简称FR)是一种基于数理统计的预测方法,FR值的大小表征各级评价因子对滑坡灾害发生的重要程度,即FR>1表明该分级区间有利于滑坡发生,FR<1表现该分级区间对滑坡的发生不利。其公式如下:
(1)
式中:ni为各分级区间内滑坡面积,N为研究区滑坡总面积,si为分类面积,S为研究区总面积。
3 略阳县域滑坡评价因子构建
3.1 建立滑坡数据库
基础数据获取方式为:①略阳县30 m×30 m的数字高程模型(DEM),从国家地理空间数据云下载(http://www.gscloud.cn),并提取坡向、曲率、坡度等评价因子。②略阳县气象站点降水量数据。③1∶50 000地质图、路网图、河流分布图在91卫图下载。④陕西省地质灾害点编录数据库。
3.2 评价因子的选取
影响滑坡形成的因素很多,根据研究区内滑坡分布特征及形成条件,选取高程(A)、坡向(B)、坡度(C)、地层(D)、地表粗糙度(E)、距断层距离(F)、曲率(G)、距道路距离(H)、地形湿度指数(I)、距河流距离(J)、降雨量(K)、地形起伏度(L)、高程变异系数(M)和地表切割深度(N)14个因素作为评价因子。
借助ArcGIS软件,将研究区划分为3 122 182个30 m×30 m的栅格。各评价指标的获取方法为:①坡向、坡度、曲率通过ArcGIS工具箱中的表面分析从 DEM 中提取。 ②地形起伏度、地表粗糙度、地形湿度指数、地表切割深度和高程变异系数通过空间分析里的栅格计算器对 DEM 处理得出。③河流通过对河流分布图矢量化获得。④道路通过对路网图进行矢量化,使用欧氏距离分析工具得到。⑤断层、地层岩性通过对1∶50 000地质图矢量化得到。
3.3 评价因子的相关性分析
进行滑坡评价模型预测时,要求各评价因子间相关性小,因而有必要进行评价因子的相关性分析。采取Spearma法得出各因子间的相关性系数(R),R值能反应各评价指标的相关性。通常将相关性分为微弱相关、低度相关、显著相关、高度相关和线性相关,所对应的R取值范围分别为|R|<0.3、0.3≤|R|<0.5、0.5≤|R|<0.8、0.8≤|R|<1、|R|=1。其公式如下:
(2)
将研究区的各评价因子的数据导入到SPSS软件中的相关性分析工具中,得到各因子相关系数(表1)。将相关性系数大于0.3的评价因子剔除掉,根据结果可知地形起伏度、高程变异系数、地表切割深度与坡度、地表粗糙度相关性高。因此,将这3项评价指标剔除,最终得到11项评价因子进行易发性评价。

表1 因子相关性系数表Tab.1 Correlation coefficient between factors
3.4 基于滑坡相对点密度(LRPD)的评价因子分析
滑坡相对点密度(LRPD)能反应灾害点与各评价因子的空间分布关系,得到不同分级状态的因子对滑坡发育的影响。LRPD值越大,则表明该分级区间是滑坡发育的有利因素,各评价因子分级的LRPD值见表2。其计算公式为:
(3)
式(3)中,mi表示因子某一分级内滑坡点个数;M表示研究区滑坡点总数;ni表示因子对应分级所占面积;N表示研究区总面积。

表2 各评价因子分级标准、频率比值及LRPD值表Tab.2 Grading standard, frequency ratio and LRPD value of each evaluation factor
3.4.1 地形地貌因子
选取的地形地貌因子为高程、坡度、坡向、曲率和地表粗糙度。采用自然间断点分类方法将高程划分为5级(图2a)(表2),在高程559~924 m内LRPD值最大,为0.383,而在高程>1 375 m范围内滑坡发育较少,仅占全部灾害点的2.47%,说明滑坡主要发生在高程中低区间的边坡上,原因是在此高程范围内的人工活动强烈、多进行切坡建房和道路建设;加上地表水及降雨的侵蚀作用,易形成地质灾害。按照方位角等间距将坡向划分为9级(图2b)(表2),其中-1~0表示水平坡,即平地,在157.5~202.5 m(正南)区间内灾害点最多,LRPD值为0.262,反映了正南朝向的边坡更容易受到光照、降雨等自然作用的影响,进而形成滑坡灾害。以相等间隔法将坡度分为5级(图2c)(表2),在坡度0°~30°内滑坡集中发育,坡度在30°以上的灾害点仅11处,在0°~10°LRPD值最大,为0.260,说明中低坡度的边坡对滑坡发育影响最大。其原因为在中低坡度处人工活动强烈,人为切坡建房及公路修建导致岩土体局部地区坡度较陡,而图层所提取出来的坡度为30×30 m地区的整体平均坡度,导致坡度值变小,但能反映出在中-低坡度为形成滑坡灾害的因素,而在平均坡度较大的地区,很少有人居住,仅在人工活动的地区构成灾害,因此,在坡度较大的区域滑坡灾害较少。曲率的大小代表边坡的类型,当曲率小于0时为凸型坡,曲率大于1时为凹型坡,曲率等于1时为直线坡(图2d)(表2)。滑坡灾害点多发生于凸坡处,占总灾害点的73.3%,LRPD值为0.181。地表粗糙度表示该地区抗侵蚀能力,指数越大,则抗侵蚀能力越强(图2e)(表2)。滑坡多发生在地表粗糙度指数较小的地貌类型处,在1~1.07分级处,LRPD值最大,表明该分级状态为滑坡的发育有利状态。
3.4.2 地质因子
地质因子包括地层岩性、距断层距离。地层岩性作为内在因子对滑坡发育起重要作用,是由于不同的岩性物理力学参数差异大,直接影响边坡的稳定性(图2f)(表2)。研究区共10套地层,而滑坡灾害点主要分布在泥盆纪、志留纪地层,占灾害点总数的62.2%。在此2处地层的LRPD值分别为0.24、0.119,表明上述2套地层对滑坡发育有利。以相等间隔法将距断层距离以1 000 m划分为5级(图2g)(表1)。滑坡灾害点主要分布在0~1 000 m内,LRPD值为0.139,表明滑坡常发育在断层构造活动带和岩土体结构软弱处。
3.4.3 道路因子
略阳县进行了大量的道路建设,破坏了原始地形、地貌,进而促进了滑坡发育。以等间隔法进行分级,将距道路的距离以500 m等分(图2h)(表2)。灾害点主要分布在0~500 m内,LRPD值为0.291。表明距离道路越近,人类活动对滑坡的发育影响越大。
3.4.4 水文因子
水文因素是滑坡形成、致灾的重要影响因素之一。水文因子包括降雨量、距河流的距离和地形湿度指数。降雨能降低岩土体的物理力学性质,使剪切强度下降,摩擦系数变小,使岩土体结构面软化,是影响滑坡发生的最重要的因子,依据自然间断点将其分为5级(图2i)(表2)。降雨量在828~867 mm时,LRPD值最大,为0.156;河流的下蚀和侧蚀作用容易侵蚀其周围的岩土体,破坏边坡的稳定性,进而为滑坡灾害的形成提供了条件;依据500 m等间隔法将距河流的距离分为5级(图2j)(表2)。灾害点分布数量与距河流距离成反比,LRPD值随距河流距离的增加而递减。地形湿度指数表示在某一流域内的土壤干湿状态(图2k)(表2);依据自然间断点法将评价因子分为5级,LRPD值在各分级中依次递增,表明地形湿度指数越大越有利于滑坡灾害的发生。
4 评价结果
4.1 基于RF模型评价结果
滑坡预测可看作一个二元分类的过程,在进行滑坡的易发性评级时,需要建立等量的正数据集(滑坡)、负数据集(非滑坡)。借助R软件中的随机选取功能,将灾害点数据集和研究区数据集导入;从445个滑坡灾害点随机选取312(70%)个正数据集与从研究区非滑坡灾害点随机选取312个负数据集作为训练集;将滑坡灾害点剩余的133(30%)个正数据集和研究区非滑坡灾害点数据集随机选取的133个负数据集作为测试集。将训练集代入RF模型进行训练,再用测试集对RF模型进行预测,得到模型的准确率为85.36%;然后将训练模型用于整个研究区,得到全区的易发性指数值,易发性指数值越高,则表明越容易发生滑坡灾害。自然断点法的原理为:通过聚类计算方式使得各分组内的相似性保持最大化,组外的相异性也最大化。将其应用于滑坡的易发性分级,通过国内外学者的研究,分类5级有较为优良的效果,能表现出滑坡易发性分组之间的差异性与组内的相似性。因此,将滑坡的易发性等级分为极低易发区、低易发区、中易发区、高易发区和极高易发区5类(图3)。
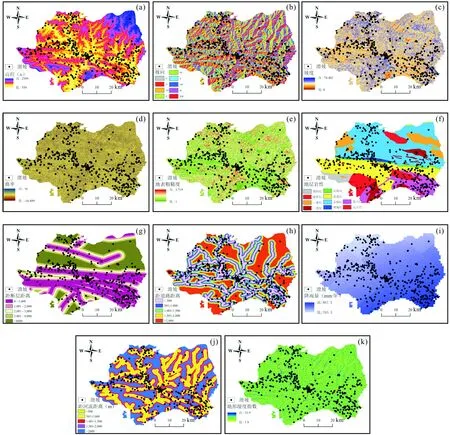
图2 评价因子分层图Fig.2 Evaluation factor classification
4.2 基于FR模型评价结果
根据FR模型方法,得出各级评价因子的频率比值,计算结果见表2。因子频率比值越大,表明滑坡易发性程度越高;最后运用 ArcGIS 栅格计算器工具将所有评价因子进行叠加,按照自然间断点法将其分为极低、低、中、高和极高易发区5类,得到基于FR模型的略阳县滑坡易发性评价区划图(图4)。

图3 基于RF模型的滑坡易发性区划图Fig.3 Landslide susceptibility map based on RF

图4 基于FR模型的滑坡易发性区划图Fig.4 Landslide susceptibility map based on FR
4.3 基于FR-RF模型评价结果
在滑坡易发性评价过程中,由于各级评价因子数据量大,而且数据类型各异,进而影响评价模型的准确性。先将各级评价因子数值采用各分级的频率比替代,则能提高数据分布的规律性;其次把评价因子的数值替换为在该分级的频率比,代入RF模型进行计算,得到基于FR-RF模型的易发性指数,模型的准确率为92.83%;将易发性指数导入ArcGIS中,得到易发性分区图(图5),按照自然间断点法将其分为极低易发区、低易发区、中易发区、高易发区和极高易发区5类。

图5 基于FR-RF模型的滑坡易发性区划图Fig.5 Landslide susceptibility map based on FR-RF
5 各评价模型的检验
将3种模型的测试样本集的易发性指数值及对应的真实类标签导入SPSS软件ROC曲线分析工具中进行分析,得到3种评价模型的预测率曲线(图6),由图6可知,FR、RF、RF-FR 3种模型下训练样本的成功率分别为 0.843、0.901、0.950。其中,RF-FR模型较其他2种模型更好,预测率比FR、RF模型分别高出0.107、0.049,可见RF-FR模型更适合研究区滑坡易发性评价。

图6 预测率曲线图Fig.6 Graph of success rate
采用ArcGIS多值提取致点工具提取各模型灾害点的易发性分级,得到灾害点在各分级内的比例(表3)。结果表明,RF-FR模型滑坡灾害点落在极高易发区、高易发区的比例为87.45%;RF、FR模型滑坡灾害点落在极高易发区、高易发区的比例分别为82.16%、71.56%。说明用RF-FR模型进行易发性评价有更佳的效果。
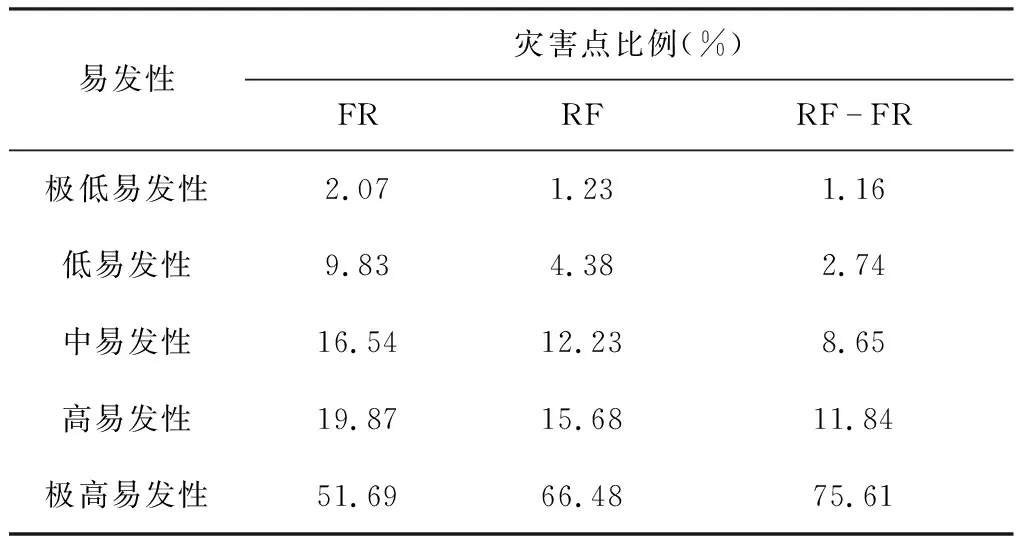
表3 各易发区灾害点比例表Tab.3 Percentages of landslide susceptibility
随机选取略阳县70个滑坡点进行实地调研,结果表明,极高、高和中易发区内分布滑坡点个数分别为53、10和7,滑坡点在低易发区与极低易发区无分布。通过与FR-RF模型中灾害点比例对比,现场调查得出的各易发区灾害点比例与其相近,验证了FR-RF模型预测结果的准确性。
6 结论
(1)根据Pearson相关系数的统计分析,地形起伏度、高程变异系数、地表切割深度与坡度的相关性系数绝对值分别为0.972、0.822、0.962,呈强相关性。剔除地形起伏度、高程变异系数和地表切割深度3项因子。
(2)基于滑坡相对点密度(LRPD)对评价因子进行分析,得出滑坡灾害点与线状因子的距离呈负相关,即距离越近,灾害点越多;反之,灾害点越少。
(3)将RF、FR 2种模型进行耦合,得到RF-FR模型。以ROC曲线对3种模型精度进行检验,结果表明,RF-FR模型测试样本的预测率比RF、FR模型分别提高了10.7%、4.9%,显示耦合模型优于单一模型,且RF-FR模型用于地质灾害易发性评价具较高的准确性与实用性。
(4)基于FR、RF和RF-FR模型,滑坡灾害点落在高易发区—极高易发区所占的比例分别为71.56%、82.16%和87.45%,得出滑坡在高—极高易发区发育较为集中,空间分布呈树枝状发育,主要集中在河流、道路所在区。
