基于半监督集成即时学习的橡胶混炼过程门尼黏度软测量研究
2022-08-29金怀平董守龙陈祥光
金怀平, 张 燕, 董守龙, 杨 彪, 钱 斌, 陈祥光
基于半监督集成即时学习的橡胶混炼过程门尼黏度软测量研究
金怀平1, 张 燕1, 董守龙2, 杨 彪1, 钱 斌1, 陈祥光2
(1. 昆明理工大学 信息工程与自动化学院, 云南 昆明 650500;2. 北京理工大学 化学与化工学院, 北京 100081)
针对工业橡胶混炼过程中门尼黏度标记数据有限,导致模型预测性能受限的问题,提出了一种半监督(SS)集成即时学习(EJIT)高斯过程回归(GPR)软测量方法,称为SSEJITGPR。当查询样本到来时,该方法通过在线迭代学习的方式获取高置信度伪标记样本,其中使用集成后的即时学习高斯过程回归(JITGPR)模型对非标记样本进行预测,并以集成预测方差作为置信度评价准则。随后,基于伪标记样本扩充后的建模数据库构建多样性的半监督JITGPR基模型。最后,采用有限混合机制实现基模型的自适应集成。与传统门尼黏度软测量方法相比,SSEJITGPR在处理局部过程特征、克服标记样本不足、预测可靠度不高等问题上表现出显著优势,其有效性和优越性通过工业案例进行了验证。
软测量;即时学习;半监督学习;集成学习;高斯过程回归;门尼黏度;橡胶混炼
1 前言
橡胶混炼是轮胎制造过程中的首要关键环节,其中门尼黏度是一个反映橡胶制品加工性能的关键性能指标[1-2]。但在实际生产中,由于缺乏可靠的在线检测设备,门尼黏度只能通过实验室离线分析获得,采样周期一般为4~6 h,测量延迟较大,不仅严重影响混炼的质量控制,而且容易造成原料浪费和经济损失。因此,准确可靠的门尼黏度在线测量对于橡胶混炼工业生产过程的监测、控制和优化至关重要。近年来,数据驱动软测量技术被广泛应用于门尼黏度信息的在线实时估计[3-6]。
常用的门尼黏度数据驱动软测量方法包括偏最小二乘(partial least squares,PLS)[3]、高斯过程回归(Gaussian process regression,GPR)[4]、极限学习机(extreme learning machine,ELM)[5]、深度学习(deep learning,DL)[6]等。然而,此类全局建模方法力求在所有过程区域上获得良好的泛化性能,无法准确描述局部过程特征,由此导致模型预测性能受限[7]。因此,基于局部建模技术的门尼黏度预测方法日益受到青睐[3-5]。
集成学习[8]和即时学习(just-in-time learning,JIT)[4-5]是2种典型的局部建模框架。它们均遵从“分而治之”的思想,通过构建局部化的预测模型,以获得更准确的预测结果。鉴于2类建模方法各有优势,将二者结合将有助于提升软测量模型预测性能,因此集成即时学习(ensemble just-in-time learning,EJIT)软测量建模研究近几年获得了较多关注[3-4]。EJIT软测量方法的基本思想是:首先构建多样性的JIT基模型并对主导变量进行估计,然后将局部预测结果融合为最终输出。尽管EJIT软测量建模框架表现出了优异的预测性能,但实际工业过程中,标记样本不足的问题仍然是制约EJIT软测量模型性能的重要因素。
在实际的橡胶混炼工业生产过程中,门尼黏度的测量成本高、周期长,可用于门尼黏度预测的标记样本严重不足。因此,门尼黏度软测量建模广泛存在标记样本不足、非标记样本丰富的现象,而传统监督式软测量方法往往忽略了对非标记样本信息的挖掘。半监督学习正是为实现同步挖掘标记和非标记样本信息以提升模型预测性能而提出的,近年来逐渐被引入软测量应用领域[9-11]。因此,研究高性能门尼黏度半监督软测量建模方法成为一个较为迫切的问题[6]。
综上,本研究提出了一种新的半监督集成即时学习高斯过程回归(semi-supervised ensemble just-in-time Gaussian process regression,SSEJITGPR)软测量建模方法。该方法框架有效融合了即时学习、半监督学习和集成学习的优势,为门尼黏度的准确预测提供了一种新的途径。主要贡献总结如下:(1)使用多种相似度指标,构建多样性的即时学习高斯过程回归(just-in-time Gaussian process regression,JITGPR)基模型,有效克服了传统即时学习使用单一相似度导致预测性能不佳的问题;(2)提出一种新的伪标记估计框架,以协同训练思想为基础,以集成即时高斯过程回归(ensemble just-in-time Gaussian process regression,EJITGPR)为预测模型,以集成预测方差为置信度评价准则,通过在线迭代学习获取高置信度伪标记样本,从而实现标记训练样本的扩充,进而构建高性能的半监督JITGPR基模型;(3)引入有限混合机制,实现多样性半监督JITGPR基模型的自适应集成。通过对工业橡胶混炼过程中门尼黏度的预测,并与传统全局/局部、监督/半监督软测量方法进行比较,充分验证了所提方法的有效性和优越性。
2 算法介绍
2.1 即时学习
即时学习,又称为懒惰学习(lazy learning)[12]或局部加权学习(locally weighted learning)[13]等,是一种能够有效处理过程非线性和时变性特征的局部学习建模框架,近年来已被广泛地应用于软测量领域。与传统的全局建模方法相比,其具有以下主要特征:(1)所有的输入数据和输出数据都存放于数据库中;(2)查询任务到来时,只根据某种相似度选择与查询样本点最相关的样本进行建模;(3)完成预测任务后,丢弃局部模型。
2.2 半监督学习
传统的监督学习方法往往需要大量的标记样本,然而在实际的工业过程中,由于技术和经济条件的限制,往往存在“标记样本缺乏、非标记样本充足”的现象,而非标记样本同样也包含大量有价值的信息,对提升预测模型性能具有重要意义。半监督学习(semi-supervised learning)[14-15]正是为解决此类问题而发展起来的。作为机器学习的一个重要分支,半监督学习允许模型在学习过程中同时使用标记样本和非标记样本来构建模型,以此提升模型的预测性能。一般而言,半监督学习可以分为5类:生成式模型(generative models)[16]、自训练(self-training)[17]、协同训练(co-training)[18]、基于图的方法(graph-based methods)[19]、半监督支持向量机(semi-supervised support vector machines, S3VM)[20]。除此之外,半监督学习和其他方法的结合近年来也受到越来越多的关注,如半监督学习和集成学习的结合[9]、半监督学习和深度学习的结合[21-22]等。此外,半监督软测量建模研究也获得了极大关注[6,9-11]。
2.3 高斯过程回归

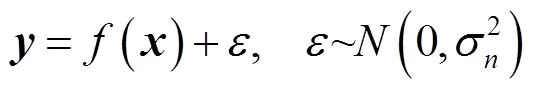

因此,高斯过程可描述为
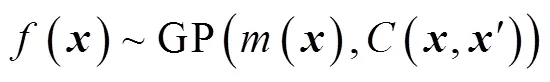
通常,对建模数据进行归一化数据预处理,假设训练样本集产生于一个零均值高斯过程:
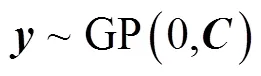


协方差函数是高斯过程回归模型的关键组成部分,在本研究中,选择带有噪声项的Matérn协方差函数,其定义如下:
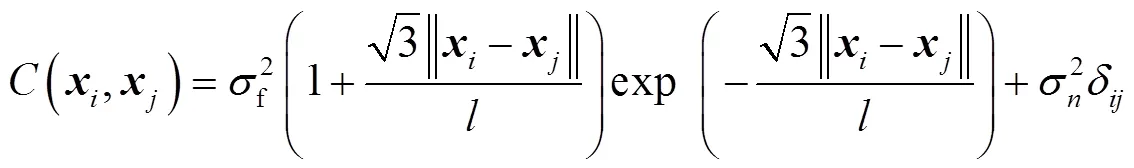
3 SSEJITGPR软测量建模
3.1 多样性相似度定义
合适的相似度函数定义是构建高性能即时学习预测模型的关键所在。相似度准则通常采用某种距离来度量查询点和历史样本之间的相似性,距离越大,相似性越低,反之亦然[24]。目前已经从不同视角定义了很多相似度指标,如基于欧氏距离(Euclidean distance,ED)[25]的相似度、基于余弦(cosine)的角度相似度等,但各种相似度性能表现不一、各有优势,难以从中选择一种适用于所有应用场景的最优相似度指标。因此,本研究定义了欧氏距离相似度、余弦相似度、协方差加权距离(covariance weighted distance,CWD)[26]相似度、皮尔逊相关系数(Pearson correlation coefficient,PCC)相似度,用于构建多样性的JITGPR基模型,综合不同相似度的优势,为构建集成即时学习软测量模型奠定基础。
欧氏距离是评价2个样本点在空间上的欧几里得距离,即样本点之间的点对点的直线距离的一种计算方法,由于其简单高效而常常作为相似度度量准则被应用于即时学习建模。其定义如下:


余弦相似度通过利用空间中两个向量之间的角度来衡量样本相似性,其定义如下:

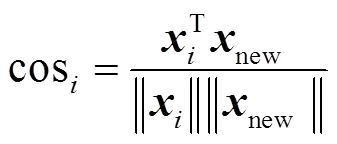
欧氏距离相似性忽略了输入变量之间的差异,为此提出了各种加权距离相似度准则,如加权欧氏距离相似度(weighted euclidean distance,WED)[27]和协方差加权距离相似度等。其中,CWD相似度同时考虑了输入变量之间以及输入和输出变量之间的关系,其定义如下:

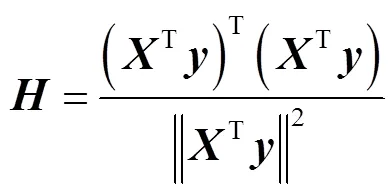
除了基于距离和基于角度的相似度评价指标,2个向量之间的相关性也能用于评价样本之间的相似性,如相关系数准则(correlation coefficient, CC)。本研究使用皮尔逊相关系数相似度作为相似度度量指标,其定义如下:
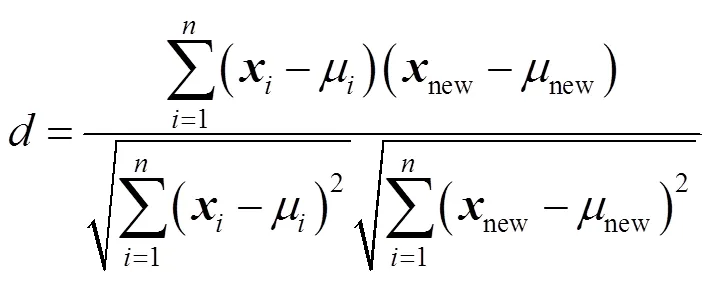
3.2 高置信度伪标记估计
标记样本缺乏是制约即时学习性能的关键因素,获取高置信度伪标记样本以扩充训练样本集是解决此问题的重要途径。典型的伪标记估计方法有自训练和协同训练2种框架,通常采用性能提升率为评价标准挑选高置信度伪标记样本。然而,此类方法需要反复重构模型以评价伪标记样本的置信度,容易造成计算时间过长、计算负担过大。而且,未考虑模型多样性的问题,导致伪标记估计精度不佳。


图1 高置信度伪标记估计获取原理图
(2) 重复以下步骤直至满足终止条件:
b) 采用2a)中所得JITGPR基模型对U¢对应的输出进行估计,获得集成预测输出和集成方差;
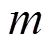
d) 更新U¢,从U¢中移除已标记的非标记样本。
在上述步骤中,多样性JITGPR基模型的融合方式至关重要,本研究采用了一种基于有限混合机制(finite mixture mechanism,FMM)[28]的自适应加权融合方法,详细原理描述如下。

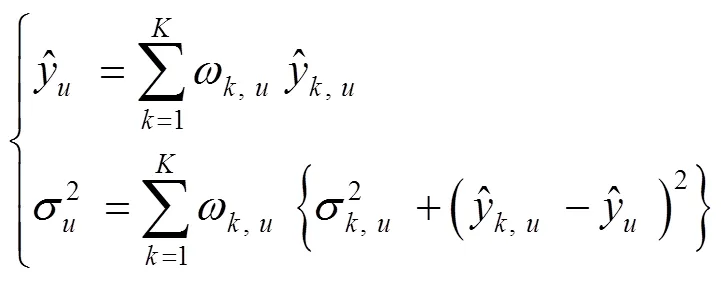
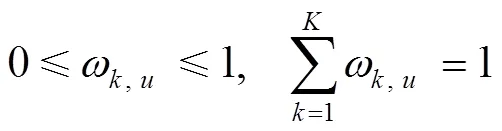

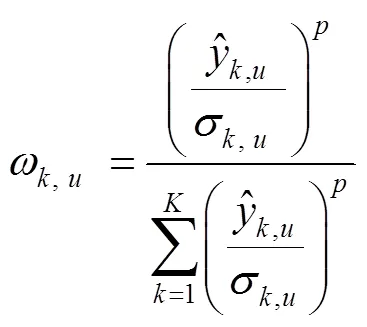
3.3 实施原理
所提SSEJITGPR软测量方法的实施原理如图2所示。
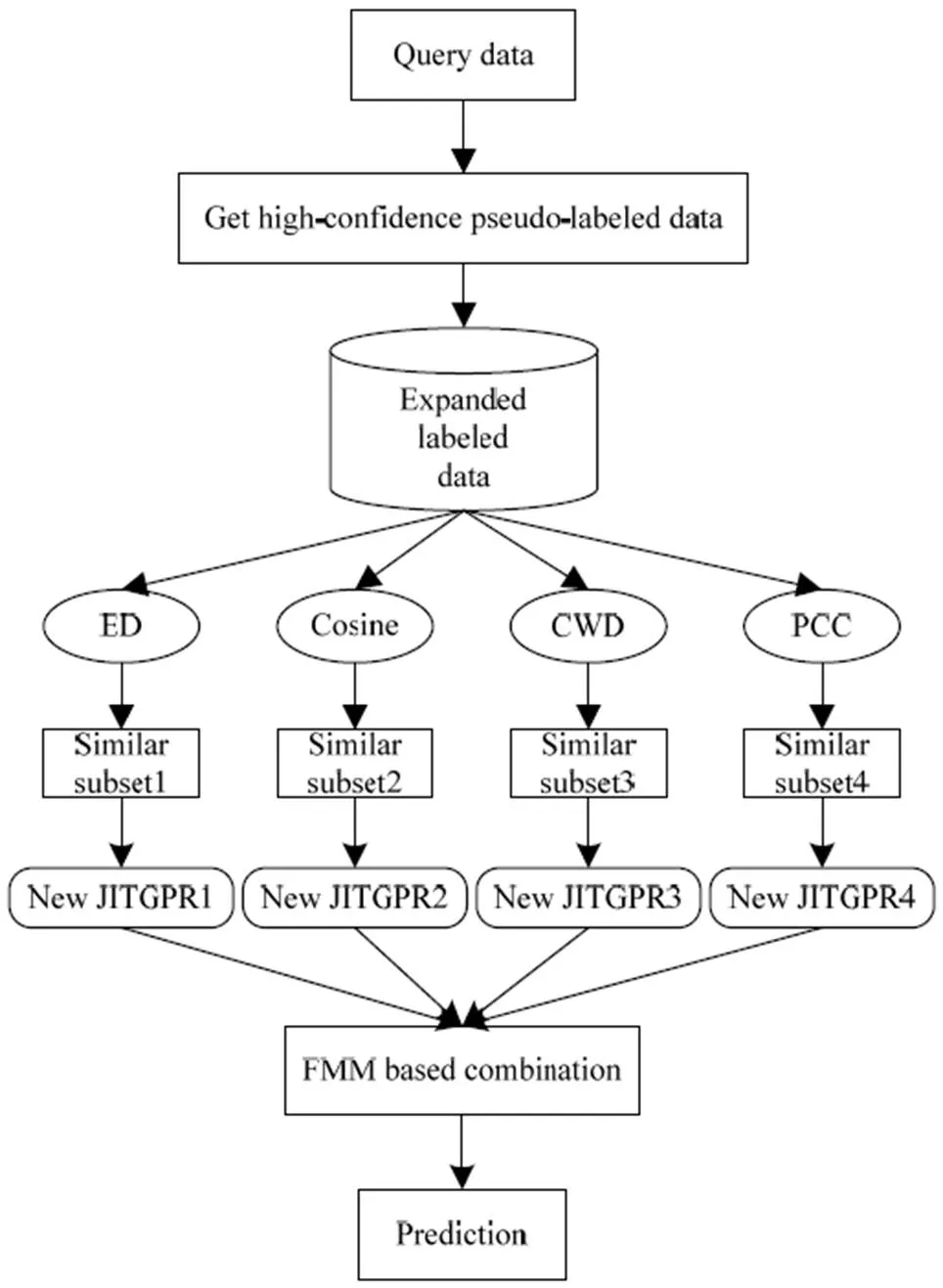
图2 SSEJITGPR软测量建模方法原理框图
实施步骤如下:
(1) 收集橡胶混炼工业过程数据并对其进行预处理,并将数据分为标记集和非标记集;
(2) 当查询样本到来时,采用3.2节所述原理获取高置信度的伪标记估计并将其添加到标记训练样本集;
(3) 使用扩充后的训练样本集,构建基于ED相似度、Cosine相似度、CWD相似度和PCC相似度的四种JITGPR基模型,并对查询样本进行预测;
(4) 使用式(16)所示的有限混合机制对局部预测结果进行自适应集成,获得集成预测均值和方差;
(5) 完成预测后丢弃已建立的模型。当下一个查询样本到来时,转到步骤(2)。
4 工业橡胶混炼过程门尼黏度预测
通过对工业橡胶混炼过程中门尼黏度的预测,验证了所提出的SSEJITGPR软测量建模方法的有效性和优越性。实验过程用于比较研究的方法如下:
(1) PLS:全局偏最小二乘模型;
(2) GPR:全局高斯过程回归模型;
(3) ELM:全局极限学习机模型;
(4) SSELM(semi-supervised extreme learning machine):全局半监督极限学习机模型;
(5) CoGPR(co-training based GPR):协同训练高斯过程回归模型;
(6) JITGPR_ED:基于欧氏距离相似度的JITGPR模型;
(7) JITGPR_Cosine:基于余弦角度相似度的JITGPR模型;
(8) JITGPR_CWD:基于协方差加权距离相似度的JITGPR模型;
(9) JITGPR_PCC:基于皮尔逊相关系数相似度的JITGPR模型;
(10) EJITGPR:使用FMM融合策略的集成JITGPR模型;
(11) SSJITGPR_ED_I/II/III/IV:使用欧氏距离相似度进行相关样本选择的半监督JITGPR软测量建模方法,其中I/II/III/IV分别代表使用ED、Cosine、CWD、PCC相似度选择非标记样本;
(12) SSJITGPR_Cosine_I/II/III/IV:使用余弦角度相似度进行相关样本选择的半监督JITGPR软测量建模方法,其中I/II/III/IV分别代表使用ED、Cosine、CWD、PCC相似度选择非标记样本;
(13) SSJITGPR_CWD_I/II/III/IV:使用协方差加权距离相似度进行相关样本选择的半监督JITGPR软测量建模方法,其中I/II/III/IV分别代表使用ED、Cosine、CWD、PCC相似度选择非标记样本;
(14) SSJITGPR_PCC_I/II/III/IV:使用皮尔逊相关系数相似度进行相关样本选择的半监督JITGPR软测量建模方法,其中I/II/III/IV分别代表使用ED、Cosine、CWD、PCC相似度选择非标记样本;
(15) SSEJITGPR _I/II/III/IV:半监督集成JITGPR模型,其中,I/II/III/IV分别代表使用ED、Cosine、CWD、PCC相似度选择非标记样本。
上述方法中,PLS、GPR、ELM属于全局监督学习模型,JITGPR_ED/Cosine/CWD/PCC属于局部监督学习模型,EJITGPR则属于集成学习模型;SSELM为全局半监督学习模型;SSJITGPR_ED/Cosine/CWD/PCC_I/II/III/IV属于半监督局部学习模型,CoGPR、SSEJITGPR_I/II/III/IV属于半监督集成学习模型。



4.1 过程描述
橡胶工业在国民经济发展中扮演着重要的角色,橡胶混炼是橡胶加工生产中的一个重要环节,本研究应用的工业橡胶混炼过程门尼黏度数据来源于华东一家轮胎生产企业。橡胶混炼是将天然橡胶或者合成橡胶、添加剂、促进剂等原材料按照某种工艺配方混合到一起,通过机械拌合作用,使它们充分且均匀地混合在一起的一种化学过程。橡胶混炼是橡胶制品生产过程中的一道重要工序,一般来说,门尼黏度是监测橡胶搅拌过程中产品质量的一个重要指标。但是在实际的工业生产过程中,每个批次的混炼过程完成后,需要4~6 h方可获得门尼黏度的离线分析值,但批混炼周期仅为2~5 min,巨大的测量延迟严重制约了混炼过程的监测、控制及优化。软测量技术是获取门尼黏度估计值的一种重要途径。考虑到橡胶混炼过程中标记样本缺乏、非标记样本丰富的现状,本研究试图建立一个高性能的半监督集成即时学习软测量模型。由于一个完整批次的橡胶混炼过程仅对应一个终点门尼黏度测量值,因此将时刻0、14、18、22、…、118 s对应的过程变量作为软测量模型的输入变量,包括混合器腔内的温度、电机功率、冲压件压力、搅拌时间、电机转速和能量等。
4.2 预测结果与分析
从集散控制系统和实验室分析中收集相应的标记和非标记样本数据,输入和输出数据中一些明显的异常值通过一个简单的3准则剔除。最后共收集到了1 172批次过程数据,其中包含800个非标记数据和372个有标记数据。将有标记数据进一步划分为训练集(150个样本)、测试集(172个样本)和验证集(50个样本)。
通过交叉验证方法确定各模型的参数如下:PLS的主成分个数为9,ELM的隐藏层数为455,SSELM的隐藏层数为170,图拉普拉斯正则项的权重系数为0.6。同时,采用经验法确定如下参数:CoGPR的迭代次数为70,每次迭代选取的高置信度伪标记数为5个,其他半监督方法的迭代次数为30,每次选择的高置信度伪标记样本数为2个,有限混合机制公式(18)中的为2。此外,对比了局部建模样本数local=5、10、15时的不同模型的预测性能。
表1比较了30种不同软测量建模方法对门尼黏度的预测结果。表中,标志“I”“II”“III”“IV”分别代表使用ED、Cosine、CWD、PCC相似度选择非标记样本。首先,不考虑半监督学习,仅对不同的监督软测量模型性能进行分析比较。可以看出,作为线性建模方法,PLS的预测性能最差,这是因为其无法有效处理过程非线性特征所致,相比而言,其他非线性建模方法的预测性能均有显著改善。但作为传统的全局建模方式,GPR和ELM的性能依然很差。相较于全局建模,基于局部学习建模原理的JITGPR_ED/Cosine/CWD/PCC软测量方法在预测性能上获得了大幅提升。例如,全局GPR的预测RMSE为5.127 0,而JITGPR_PCC的预测RMSE仅为4.149 0,预测精度提升了19.08%。此外,可以看出,在即时学习中,当选取相同的局部样本数进行建模时,使用4种不同相似度指标的JITGPR预测结果具有显著差异,而且由表1数据可以看出,在不同的局部建模样本下,没有哪一种相似度始终能保持最佳的预测性能。因此,为克服使用单一相似度导致的预测局限性,引入集成学习方法,将使用4种相似度的JITGPR基模型融合为EJITGPR模型。不难看出,local=5和10时,EJITGPR的预测性能均优于使用单相似度的JITGPR预测性能,local=15时,EJITGPR预测性能接近最佳的单相似度JITGPR模型。这些结果充分表明,通过融合集成学习和即时学习,EJIT软测量建模框架的性能显著优于传统全局和局部建模方法。

表1 不同软测量建模方法的门尼黏度预测结果
对比分析引入半监督学习以后的门尼黏度预测性能。可以看出,相比于ELM,SSELM由于使用了非标记信息,其性能获得了改善。但相比于GPR,CoGPR的性能变得更差,这可能是因为高置信度伪标记样本选择不当所致。对于局部建模方法而言,当使用本研究所提伪标记估计方法扩充标记样本库之后,所有JITGPR模型均获得了不同程度的性能提升。例如,local=5、10、15时,监督模型JITGPR_ED的预测RMSE分别为4.437 7、5.767 8、6.949 6,但引入高置信度伪标记样本后,半监督模型SSJITGPR_ED_I的预测RMSE变为4.082 5、3.827 0、4.376 5,可见预测误差获得了大幅削减,这充分证明了半监督学习在提升模型预测性能方面的有效性。此外,图3比较了JITGPR与SSJITGPR的预测结果误差曲线图。如图可见,与JITGPR相比,在大多数情况下SSJITGPR的误差幅值要小得多,说明引入半监督学习以后,模型的预测性能得到了显著改善。

图3 JITGPR与SSJITGPR软测量建模方法预测结果误差曲线图(nlocal =10)
从上面的分析可以看出,SSJITGPR表现良好。为了获得鲁棒性更好、可靠性更高的预测结果,再次引入集成学习,将使用不同相似度的SSJITGPR基模型进行融合,以期获得表现更佳的SSEJITGPR软测量模型。从表1中可以看出,使用不同的相似度选择非标记样本时,SSEJITGPR的预测性能比较接近。同时也可以看出,在某些应用场景下,SSEJITGPR的预测性能并未超过性能最佳的单一相似度SSJITGPR模型。这触发一种直观想象:是否可以选用一种表现最佳的单相似度SSJITGPR模型替代SSEJITGPR模型?虽然事实上确实存在比SSEJITGPR性能更佳的SSJITGPR模型,但是实际应用中却很难从中挑出一种单相似度SSJITGPR模型在所有应用场景下均表现最优。反观SSEJITGPR,根据表1结果,在不同的应用场景下,SSEJITGPR均获得了比所有SSJITGPR更佳或者非常接近最佳SSJITGPR的预测性能。因此,集成学习的引入能有效降低SSJITGPR因为相似度选择不当而造成性能较差的风险。为了直观评价SSEJITGPR的预测性能,图4给出了使用该方法获得的门尼黏度预测结果趋势曲线。可以看出,门尼黏度预测值和实际值高度吻合,这进一步表明了所提方法的有效性。
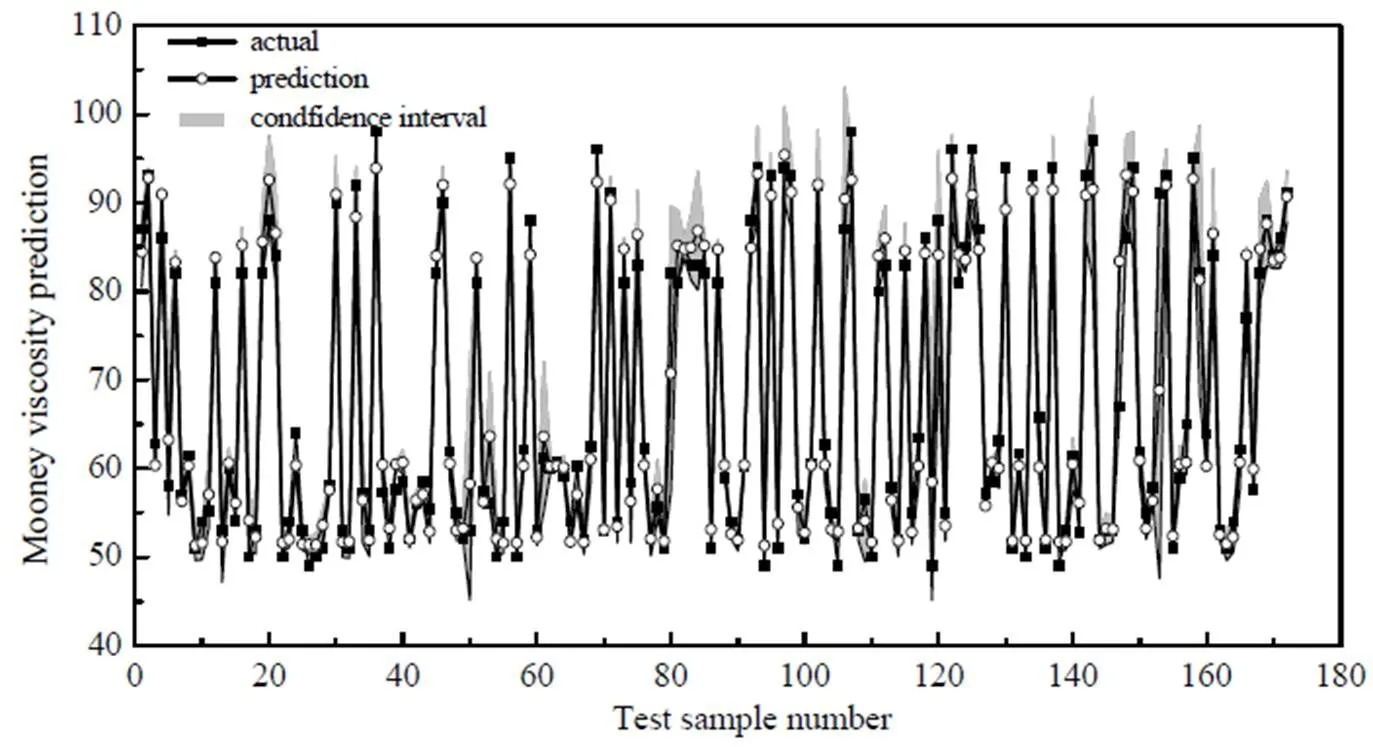
图4 SSEJITGPR建模方法对门尼黏度的预测结果趋势曲线(nlocal =10)
此外,图5比较了不同的JITGPR和SSEJITGPR在不同局部建模规模下的预测性能。从图中看出,相比于各种单相似度的JITGPR基模型,融合集成学习和半监督学习的SSEJITGPR模型表现更佳,特别是随着局部建模样本的增加,这种优势更为明显。同时可以看出在不同局部建模规模下,使用不同相似度的JITGPR模型性能排序并不一致,因此也说明,选择集成学习策略是十分必要的。此外,从性能退化趋势走向上来看,与JITGPR软测量建模方法相比,本研究所提方法对局部建模样本规模的敏感程度要低很多。这些结果再次表明,与传统的即时学习软测量建模方法相比,本研究所提方法对橡胶混炼过程中门尼黏度的预测结果更为准确和可靠。
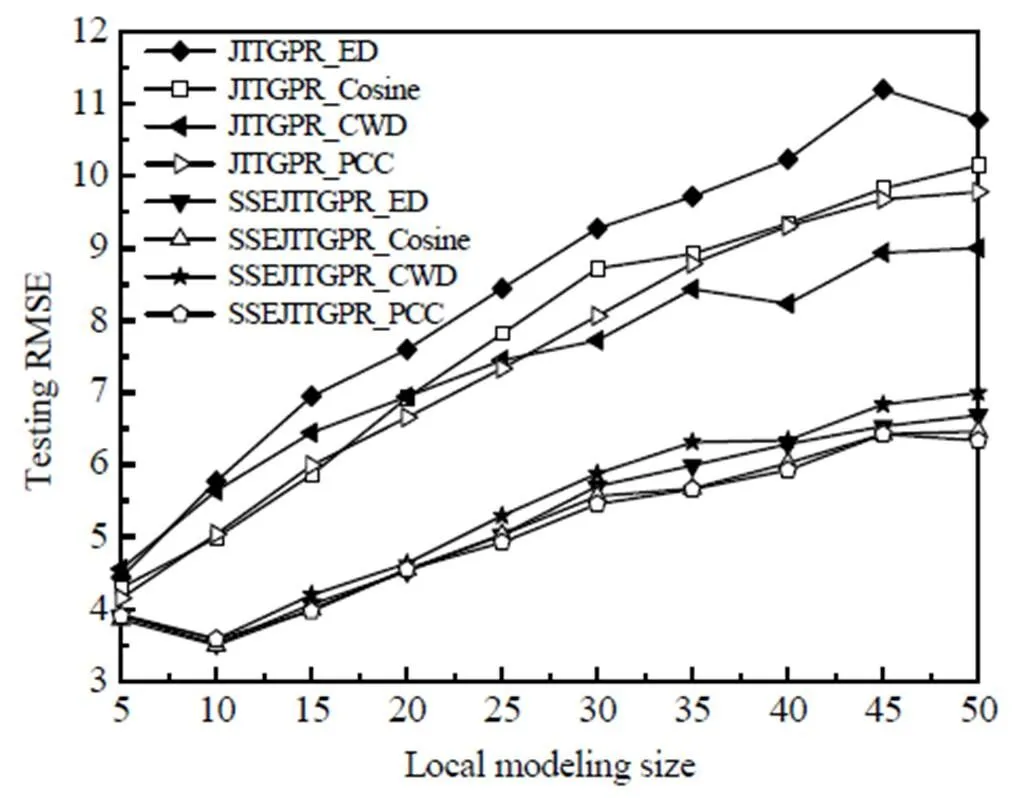
图5 使用不同模型和不同局部建模样本数的门尼黏度预测性能比较
5 结论
本研究提出了一种新的用于工业橡胶混炼过程中门尼黏度预测的半监督集成即时学习软测量建模方法SSEJITGPR。该方法以GPR为基学习器,通过使用多种相似度指标构建多样性的JITGPR基模型,然后使用有限混合机制对基模型进行融合。同时,引入半监督学习,基于集成预测方差选择高置信度的伪标记样本以扩充标记样本集,从而提升JITGPR基模型的预测性能。该方法有效融合了即时学习、半监督学习、集成学习的优势,因此在橡胶混炼过程门尼黏度预测中的表现显著优于传统全局/局部、监督/半监督模型。在后续的工作中,以下问题值得进一步深入研究:如何自适应确定即时学习的局部建模样本数;如何通过其他方法获取高置信度的伪标记样本;如何以其他多样性扰动方式构建同时具有多样性和准确性的基模型;如何通过其他高效的集成策略来实现模型的有效融合。
[1] ZHANG Z, SONG K, TONG T P,. A novel nonlinear adaptive Mooney-viscosity model based on DRPLS-GP algorithm for rubber mixing process [J]. Chemometrics & Intelligent Laboratory Systems, 2012, 112: 17-23.
[2] LIU Y, GAO Z L. Real-time property prediction for an industrial rubber-mixing process with probabilistic ensemble Gaussian process regression models [J]. Journal of Applied Polymer Science, 2015, 132(6): 41432.
[3] 金怀平, 李建刚, 钱斌, 等. 基于多模态扰动的集成即时学习软测量建模 [J]. 信息与控制, 2020, 49(3): 257-266.
JIN H P, LI J G, QIAN B,. Soft sensor development based on ensemble just-in-time learning with multimodal perturbation [J]. Information and Control, 2020, 49(3): 257-266.
[4] JIN H P, LI J G, WANG M,Ensemble just-in-time learning-based soft sensor for Mooney viscosity prediction in an industrial rubber mixing process [J]. Advances in Polymer Technology, 2020, 2020(1): 1-14.
[5] JIN W Y, LIU Y, GAO Z L. Fast property prediction in an industrial rubber mixing process with local ELM model [J]. Journal of Applied Polymer Science, 2017, 134(41): 45391.
[6] ZHENG S, LIU K, XU Y,. Robust soft sensor with deep kernel learning for quality prediction in rubber mixing processes [J]. Sensors, 2020, 20(3): 695.
[7] 刘毅. 间歇过程的核学习自适应建模与控制研究及工业应用 [D]. 杭州: 浙江大学, 2009.
LIU Y. Research on kernel learning adaptive modeling and control for industrial batch processes [D]. Hangzhou: Zhejiang University, 2009.
[8] 金怀平, 黄思, 王莉, 等. 基于进化多目标优化的选择性集成学习软测量建模 [J]. 高校化学工程学报, 2019, 33(3): 680-691.
JIN H P, HUANG S, WANG L,. Selective ensemble learning based on evolutionary multi-objective optimization for soft sensor development [J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(3): 680-691.
[9] JIN H P, LI Z, CHEN X G,. Evolutionary optimization based pseudo labeling for semi-supervised soft sensor development of industrial processes [J]. Chemical Engineering Science, 2021, 237: 116560.
[10] 李东, 刘乙奇, 黄道平. 基于Tri-training MPLS的半监督软测量模型 [J]. 华东理工大学学报(自然科学版), 2021, 47(2): 217-224.
LI D, LIU Y Q, HUANG D P. Semi-supervised soft sensor model based on Tri-training MPLS [J]. Journal of East China University of Science and Technology, 2021, 47(2): 217-224.
[11] GUO R, LIU H. Semisupervised dynamic soft sensor based on complementary ensemble empirical mode decomposition and deep learning [J]. Measurement, 2021, 183: 109788.
[12] AHA D W. Lazy learning [M]. Berlin: Springer Science & Business Media, 1997.
[13] YIN S, XIE X, SUN W. A nonlinear process monitoring approach with locally weighted learning of available data [J]. IEEE Transactions on Industrial Electronics, 2016, 64(2): 1507-1516.
[14] SHAHSHAHANI B M, LANDGREBE A. The effect of unlabeled samples in reducing the small sample size problem and mitigating the Hughes phenomenon [J]. IEEE Transactions on Geoscience & Remoto Sensing, 1994, 32(5): 1087-1095.
[15] ZHU X J, GOLDBERG A B. Introduction to semi-supervised learning [J]. Synthesis Lectures on Artificial Intelligence and Machine Learning, 2009, 3(1): 1-130.
[16] FUJINO A, UEDA N, SAITO K,Semisupervised learning for a hybrid generative/discriminative classifier based on the maximum entropy principle [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2008, 30(3): 424-437.
[17] YAROWSKY D. Unsupervised word sense disambiguation rivaling supervised methods: 33rd Annual Meeting of the Association for Computational Linguistics [C]. Massachusetts: Association for Computational Linguistics, 1995: 189-196.
[18] BLUM A, MITCHELL T. Combining labeled and unlabeled data with co-training: Proceedings of the Eleventh Annual Conference on Computational Learning Theory [C]. New York: Association for Computing Machinery, 1998: 92-100.
[19] SINDHWANI V, NIYOGI P, BELKIN M. Beyond the point cloud: from transductive to semi-supervised learning: Proceedings of the 22nd International Conference on Machine Learning [C]. New York: Association for Computing Machinery, 2005: 824-831.
[20] VAPNIK V N. An overview of statistical learning theory [J]. IEEE Transactions on Neural Networks, 1999, 10: 988-999.
[21] SUN Q, GE Z. A survey on deep learning for data-driven soft sensors [J]. IEEE Transactions on Industrial Informatics, 2021, 17(9): 5853-5866.
[22] LUO Y C, ZHU J, LI M X,. Smooth neighbors on teacher graphs for semi-supervised learning: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition [C]. Salt Lake City: IEEE Computer Society, 2018: 8896-8905.
[23] JIN H P, SHI L X, CHEN X G,. Probabilistic wind power forecasting using selective ensemble of finite mixture Gaussian process regression models [J]. Renewable Energy, 2021, 174: 1-18.
[24] YUAN X F, ZHOU J, WANG Y L,. Multi-similarity measurement driven ensemble just-in-time learning for soft sensing of industrial processes [J]. Journal of Chemometrics, 2018, 32(10): e3040.
[25] KIM S, KANO M, HASEBE S,. Long-term industrial applications of inferential control based on just-in-time soft-sensors: Economical impact and challenges [J]. Industrial & Engineering Chemistry Research, 2013, 52(35): 12346-12356.
[26] HAZAMA K, KANO M. Covariance-based locally weighted partial least squares for high-performance adaptive modeling [J]. Chemometrics and Intelligent Laboratory Systems, 2015, 146: 55-62.
[27] KIM S, OKAJIMA R, KANO M,. Development of soft-sensor using locally weighted PLS with adaptive similarity measure [J]. Chemometrics and Intelligent Laboratory Systems, 2013, 124: 43-49.
[28] FRUHWIRTHSCHNATTER S. Finite mixture and Markov switching models [M]. New York: Springer, 2006.
Study on semi-supervised ensemble just-in-time learning based soft sensing of Mooney viscosity in rubber mixing process
JIN Huai-ping1, ZHANG Yan1, DONG Shou-long2, YANG Biao1, QIAN Bin1, CHEN Xiang-guang2
(1. Faculty of Information Engineering and Automation, Kunming University of Science and Technology, Kunming 650500, China;2. School of Chemistry and Chemical Engineering, Beijing Institute of Technology, Beijing 100081, China)
Traditional soft sensors for Mooney viscosity estimation in industrial rubber mixing process often encounter the scarcity of labeled data, thus leading to great difficulties in obtaining accurate estimations. Therefore, a semi-supervised (SS) ensemble just-in-time (EJIT) learning based Gaussian process regression (GPR) method referred to as SSEJITGPR was proposed. When a query sample comes, a set of diverse just-in-time Gaussian process regression (JITGPR) base models is constructed and combined to predict unlabeled samples for providing high-confidence pseudo-labeled samples through iterative learning, where the ensemble prediction variance is used for confidence evaluation. Then, a group of diverse semi-supervised JITGPR base models is built from the modeling database extended by the selected pseudo-labeled data. Finally, a finite mixture mechanism is used to realize the adaptive combination of the base models. Compared with the traditional methods for Mooney viscosity estimation, SSEJITGPR showed significant advantages in dealing with local process characteristics, overcoming scarcity of labeled data and low prediction reliability. The effectiveness and superiority of SSEJITGPR has been verified by an industrial application case.
soft sensor; just-in-time learning (JIT); semi-supervised learning; ensemble learning; Gaussian process regression; Mooney viscosity; rubber mixing process
TP277
A
10.3969/j.issn.1003-9015.2022.00.008
1003-9015(2022)04-0586-11
https://kns.cnki.net/kcms/detail/33.1141.TQ.20220523.1546.002.html
2021-07-17;
2021-11-19。网络首发时间:2022-05-23 17:25:20
国家自然科学基金(62163019,61763020,61863020);云南省应用基础研究计划(202101AT070096)。
金怀平(1987-),男,云南宣威人,昆明理工大学副教授,博士。
金怀平,E-mail:jinhuaiping@126.com
金怀平, 张燕, 董守龙, 杨彪, 钱斌, 陈祥光. 基于半监督集成即时学习的橡胶混炼过程门尼黏度软测量研究[J]. 高校化学工程学报, 2022, 36(4): 586-596.
:JIN Huai-ping, ZHANG Yan, DONG Shou-long, YANG Biao, QIAN Bin, CHEN Xiang-guang. Study on semi-supervised ensemble just-in-time learning based soft sensing of mooney viscosity in rubber mixing process [J]. Journal of Chemical Engineering of Chinese Universities, 2022, 36(4): 586-596.
