面向船舶智能喷涂系统中物料供应平台的避障控制及其仿真

2022-08-29盛卓然刘金锋

江苏科技大学学报(自然科学版) 2022年3期

盛卓然, 刘金锋

(1.墨尔本大学工程与信息技术学院(FEIT)，墨尔本 3010)(2.江苏科技大学机械工程学院，镇江 212100)

机器人技术在船舶建造领域已得到广泛的研究与实践.涂装是船舶建造过程中的重要环节，且喷涂过程会对人体健康造成损害，研发各类涂装装备代替人工涂装的作业模式是未来发展趋势[1].船舶智能喷涂系统由物料供应平台和智能喷涂平台两大子系统构成，其中物料供应平台负责油漆耗材的运载任务，在喷涂作业时持续地为后者提供油漆物料，这要求物料供应平台能够自主跟随智能喷涂平台.而船舶的喷涂作业多在干船坞中进行，干船坞内环境复杂且有较多障碍物，如钢结构、云梯车等，因此物料供应平台的避障能力是实现系统智能喷涂的关键.文中以物料供应平台的自主跟随与避障为研究对象，开发相应跟随避障控制器.

目前国内外已有多种可行的避障控制算法，如人工势场算法[2]、Bug算法[3]、向量势直方图法[4]、动态窗口法[5]以及模糊控制法[6]等.移动机器人运动学模型的非线性与时变性[7]，以及环境中的障碍物具有位置、形状、尺寸的未知性，会给移动机器人避障造成困难.在上述的避障算法中，人工势场算法存在局部最小点问题[8]，即当某一点的引力势场与斥力势场相等时，移动机器人会陷入停滞；对于Bug算法，其前提条件是将机器人视为一个点，对传感器准确度的敏感性较高，因此当被控对象的运动学模型复杂或传感器噪声较大时，移动机器人的避障能力将受到影响；向量势直方图法中的阈值较难确定，过低或过高的阈值都会导致移动机器人避障失败；动态窗口法会使移动机器人陷入稠密的障碍物中无法脱困[9]；模糊控制法作为以人工经验为基础的控制算法，其核心思想是将复杂的整体逻辑划分为多个简单的逻辑块[10]，并用一组模糊规则进行控制.将模糊控制算法用于移动机器人避障时，具有不需要被控对象的精准数学模型、构造相对容易、易于软件实现、鲁棒性和适应性好[11]等特点，故能胜任对物料供应平台的避障控制.

1 物料供应平台的基础设计与研究

1.1 智能喷涂系统概述及传感器的布置

智能喷涂系统由智能喷涂平台和物料供应平台两个部分组成，其工作状态如图1.智能喷涂平台的载体为一架六旋翼无人机，作业过程中无人机挂载喷枪沿船体侧舷飞行；物料供应平台为的载体为两轮差动小车，其用途为运载油漆耗材，并由一根软管与智能喷涂平台连接为其输送油漆.该系统的工作方式要求物料供应平台能够实现以下两项功能：一是自主跟随智能喷涂平台的无人机；二是自主规避沿途的障碍物.

图1 智能喷涂系统的工作状态Fig.1 Working status of the intelligent spraying system

为实现物料供应平台的自主避障，需获取平台与障碍物的相对距离信息.考虑到平台的不同航向角可能同时存在障碍物的情况，故在该平台的正向180°均匀地布置有编号1～8的超声波传感器，以保证传感器的探测密度.物料供应平台的小车底盘模型与实物如图2.

图2 超声波传感器的布局Fig.2 Layout of ultrasonic sensors

1.2 两轮差速小车的运动学分析

智能喷涂系统的物料供应平台载体为两轮驱动小车，主动轮A、B安装在车头两侧，以两轮差速旋转的方式改变小车的位姿状态.为有效分析该小车前进、转向等运动特性，对其进行运动学分析.该两轮差速小车的运动学模型如图3.

图3 两轮差动小车运动学模型Fig.3 Kinematics model of the two-wheel differential trolley

记两轮间距为d.在某一时刻t，经过极小时间变量Δt后小车左右驱动轮的中点由M1位置移动至M2位置，两轮轴线由x轴逆时针旋转角度θ1，左轮中心点由A1移动至A2，右轮中心点由B1移动至B2.若已知该时刻左、右轮的转速分别为ω1和ω2，则左、右轮行驶的弧度距离分别为：

(1)

当Δt→0时，θ1=θ2→0，则A2B2=A2C=d,由几何关系可得：

(2)

记t至t+Δt时刻小车的航向角的变化量为α，由几何关系可知α=θ1=θ2，可得小车两轮中点的角速度为：

(3)

设小车左右轮的半径均为r，则t时刻小车左右轮的线速度分别为：

(4)

两轮的线速度方向永远平行于同一条直线，因此左右轮中点的线速度为：

(5)

由式(3，5)，物料运载平台的两轮差动小车运动特征见表1.

表1 两轮差动小车运动特征

2 物料供应平台的控制系统设计

2.1 物料供应平台的整体控制流程

物料供应平台的控制系统由避障控制和跟随控制两部分构成，整体构架如图4.

图4 控制系统构架Fig.4 Architecture of the control system

在该控制系统中，物料供应平台与智能喷涂平台的相对位置信息被输入至跟随控制器，同时其与障碍物的相对距离信息被输入至避障控制器.

两种控制器的输出信号经过跟随、避障优先度的判断后，取优先度较高者传输给小车的驱动轮，物料供应平台随即执行跟随或避障行驶，而行驶过程中小车与无人机、障碍物之间位置、距离也实时地作为反馈信息输入控制器，最终实现物料供应平台的跟随、避障功能.为使物料供应平台在目标跟随和障碍物规避之间不顾此失彼，需要对两种控制器进行优先度判断，其判断逻辑如图5.

图5 跟随、避障优先度的判断逻辑Fig.5 Judgment logic of the priority of following and avoiding obstacles

2.2 避障控制设计

文中避障控制器为三输入两输出的模糊逻辑控制器，模糊推理方法采用似然推理中常用的Mamdani推理法，去模糊化则采用centroid法[12].该避障控制器有两个关键技术点：其一是输入信号的合理简化；其二是制定合理的避障规则表，这需要将模糊推理与现实世界中人类驾驶习惯相结合.

对于关键技术点1，考虑到物料供应平台的小车底盘在正半圆安装有多个超声波传感器，若将每个传感器的距离信息都作为单独的输入量，则会造成输入量过多，模糊规则数量激增且分类复杂的问题，从而影响小车的避障的反应速度，增加对运算资源的占用[13].因此将8个传感器分为左、前、右3组，分别记为left(1～3号传感器)、front(4、5号传感器)、right(6～8号传感器).在实际运作中，取每组全部传感器中距离信息的最小值，如left=min(1～3号传感器)，作为该组的数值输入至模糊控制器，由此模糊控制器的输入量可由8个减少至3个.同时，输出量为物料供应平台小车的左右驱动轮转速，记为leftM和rightM.最终的模糊控制器如图6.

图6 三输入两输出模糊控制器Fig.6 Three-input and two-output fuzzy controller

由于3个输入量都为距离信息，且各组中的超声波传感器探测性能相同，因此每个输入量的模糊子集均为“距离很近”，“距离较近”，“距离远”，分别记为“HJ”，“J”，“Y”，论域则为0～1 m.而模糊控制器的输出量为驱动轮转速，且考虑到需要小车实现前进、左右急转弯、左右转弯和原地旋转的功能，因此输出量的模糊子集为“反转”，“低速正转”，“高速正转”，分别记为“F”，“M”，“K”，论域为-1～1 m/s.

而关键技术点2中的模糊规则表是模糊控制理论的核心部分，直接影响小车实际的避障性能.使用if-and-then逻辑语言制定出规则如表2.将全部的规则录入Matlab的Fuzzy logic工具箱便得到模糊规则系统如图7.以设定的传感器距离信息为例，当左侧、前方和右侧与障碍物的距离分别为0.26，0.02，0.02 m时(左、前、后距离障碍物很近)，左轮转速为-0.2 m/s，右轮转速为0.2 m/s，此时小车原地旋转寻找无障碍物的方向作为出口.最终将该模糊控制器生成.fis文件，为后续仿真实验使用.避障控程序的执行流程如图8.

表2 避障模糊规则表

图7 模糊规则系统Fig.7 Fuzzy rule system

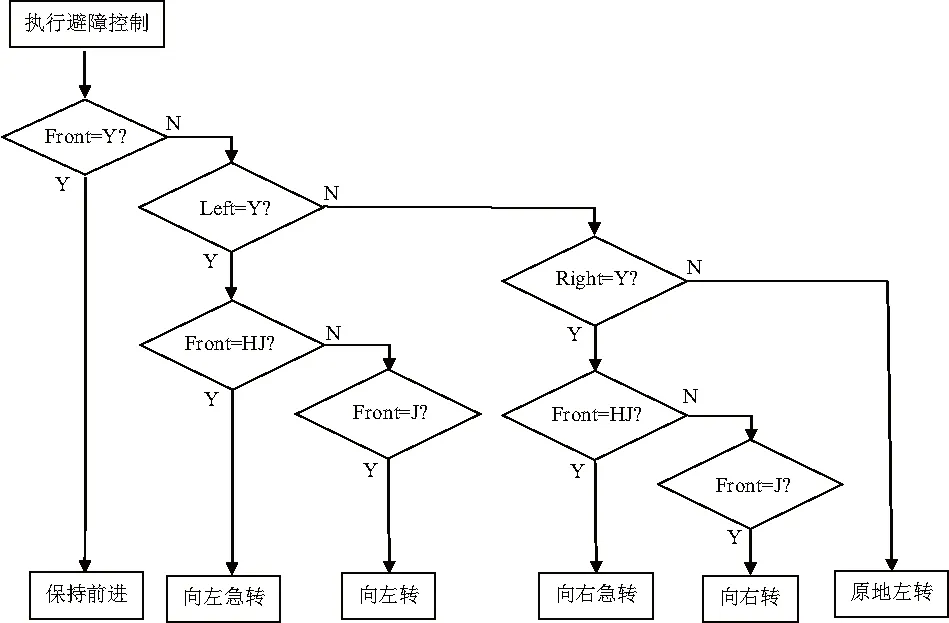
图8 避障控制程序流程Fig.8 Flow chart of the obstacle avoidance control program

2.3 跟随控制设计

为实现物料供应平台对智能喷涂平台的自主跟随能力，基于PID控制算法设计了跟随控制器.当智能喷涂平台按既定任务飞行时，其与物料供应平台之间的距离关系与角度关系均为时变的量，若要实现小车对无人机的自主跟随，则需要在距离与角度两个方面实时地调整小车左右驱动轮的转速.假设在某一时刻物料供应平台的小车与智能喷涂平台的无人机在x-y平面(不计z方向的高度差)的位置关系如图9.

图9 小车与无人机在x-y平面内的位置关系Fig.9 Positional relationship between the trolley and the drone in the x-y plane

记小车和无人机的中心点在x-y平面内的坐标分别为O1：(x1，y1)和O2：(x2，y2)，则二者中心点的距离和角度如式(6、7)，PID跟随控制器以上述的“L”、θ为输入量，小车左、右驱动轮的转速为输出量，得：

(6)

(7)

由PID控制原理，可以得出小车左右驱动轮转速的表达式为：

(8)

式中：KPL、KPθ为L、θ各自的比例环节增益系数，其决定系统达到稳态所需的幅值变化量；KIL、KIθ为L、θ各自的积分环节增益系数，其决定系统达到稳态的速度；KDL、KDθ为L、θ各自的微分环节增益系数，其决定系统的稳定性.

PID控制器性能的优劣取决于各参数的取值，文中采用3组不同的取值进行对比测试，取值如表3.

表3 跟随控制器的PID增益参数取值

设L、θ的初态分别为2.705 8 m和1.443 6 rad.当系统达到稳态，即物料供应平台与智能喷涂系统的中心重合时，3种增益参数的时域变化图像和跟随控制结果如图10、11.

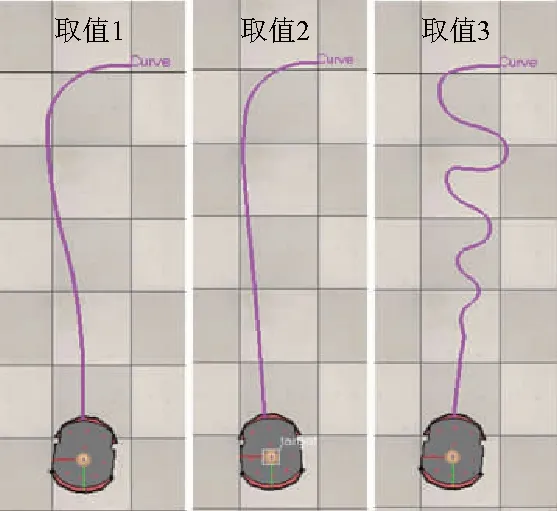
图10 3组PID增益参数取值的跟随轨迹Fig.10 Following trajectories of three groups of different PID gain parameter values

图11 3组PID增益参数取值的时域变化图像

由上述对比可知，虽然取值3达到稳态的速度最快，耗用步数为60，但其存在明显的振荡区间，这不利于复杂环境下对障碍物的规避；取值2为单纯的比例调节，无积分、微分环节，虽然该取值能平滑且无振荡地到达稳态，但耗时最长(160步数)；而取值1在保证无振荡的前提下能够较快地达到稳态(75步数)，其结果便是物料供应平台对智能喷涂系统能够做到平稳且快速的跟随.

3 仿真实验

3.1 实验方法及步骤

为验证跟随与避障控制方法的可行性，以Matlab和CoppeliaSim为软件平台经行联合仿真实验.其中Matlab软件负责运行控制程序，CoppeliaSim软件凭借其良好的物理引擎负责实时呈现物料供应平台的运动轨迹.在CoppeliaSim软件中构建仿真实验环境，如图12.该实验环境由以下部分构成：待喷涂作业的船体、干船坞中常见的障碍物(云梯车、集装箱、油漆桶)、智能喷涂平台以及物料供应平台.

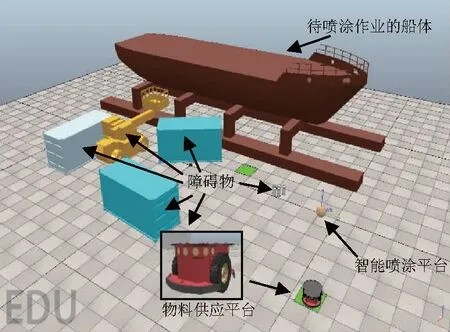
图12 仿真实验环境Fig.12 Simulation experiment scene

CoppeliaSim软件robots-moblie模型库中的Pioneer_p3dx小车[14]与智能喷涂系统中的物料供应平台具有相同的运动学结构以及传感器的布局，故在实验中使用该小车模拟物料供应平台.Matlab与CoppeliaSim的联合仿真需要搭建二者的远程API通信[15].其具体步骤如下：

步骤1 新建项目文件夹，将该文件夹添加至Matlab路径.

步骤2 将CoppeliaSim根目录中的remApi.m、remoteApi.dll以及remoteApoProto.m文件添加至步骤1的Matlab路径.

步骤3 将CoppeliaSim构建的虚拟仿真环境的.ttt文件添加至项目文件夹.

步骤4 在Matlab端控制程序中编写连接远程通信的关键代码.

为实现控制程序对实验环境中物料供应平台的控制，需要CoppeliaSim端将小车、障碍物之间的距离信息以及小车、无人机之间的相对位置信息与Matlab端实时共享，同时Matlab端的控制程序也需根据这些信息实时地调整小车的车轮转速.参考CoppeliaSim用户手册中的Remote API functions (Matlab)部分，可得到以下具体步骤：

步骤1 使用vrep.simxGetObjectHandle函数获得CoppeliaSim环境中各部件的句柄以获得对应的控制权限.

步骤2 使用vrep.simxReadProximitySensor函数读取各传感器与障碍物的距离信息，将数值赋予变量us1至us8，并按照2.2节中的传感器分组方法将us1至us8变量列入数组LD，FD和RD作为避障控制器的输入量.

步骤3 使用vrep.simxGetObjectPosition函数和vrep.simxGetObjectOrientation函数获得小车与无人机之间的相对位置关系，并将数值赋予变量position与angle作为跟随控制器的输入量.

步骤4 将上述输入量的值带入避障和随动控制器，其中避障控制器使用readfis函数读取2.2节中创建好的.fis文件.

步骤5 使用vrep.simxSetJointTargetVelocity函数将各控制器的输出量传回CoppeliaSim环境为小车的驱动轮赋值.

步骤6 分别点击CoppeliaSim端与Matlab端的运行按钮，进行仿真实验.

具体实验过程为：实验开始时物料供应平台处于起始点，智能喷涂平台悬停在小车正上方；随后智能喷涂平台由起始点飞行至停留点并悬停，物料供应平台进行自主避障、跟随至停留点并停下，最后智能喷涂平台飞至终点上方，物料供应平台跟随至终点并终止行驶，实验结束.

3.2 实验结果及分析

起点、停留点、终点之间物料供应平台的跟随避障效果如图13，最终完整的实验轨迹图如图14.物料供应平台在跟随智能喷涂系统行驶的过程中避障5次，碰撞0次.

图13 物料供应平台在起始点、停留点、终点之间的跟随与避障效果Fig.13 Following and obstacle avoidance results of thematerial supply platform between the starting point, the stop point and the end point

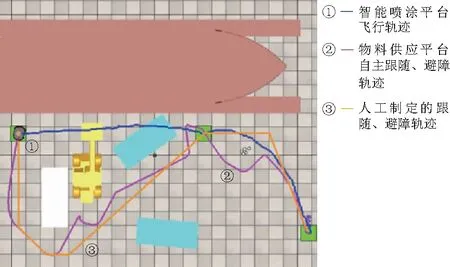
图14 实验轨迹图Fig.14 Track diagram of experimental result

将模糊控制的结果与相同情况下人工操作的结果进行比较可以验证模糊控制器设计的合理性.由图14可见，物料供应平台的自主行驶轨迹与人工制定的轨迹在总体方向上保持一致.3条轨迹路线的对比如表4.

表4 行驶距离对比

由于智能喷涂系统在障碍物上方飞行，因此路线长度最短.而物料供应平台自主跟随、避障的路线长度与人工制定的理想路线长度之间的差别为11.4%.此外，物料供应平台和智能喷涂系统之间的水平距离L随仿真时间t的变化关系如图15，可见L的最大值控制在4.3 m内，且在停留点和终点处的中心完全重合，说明跟随效果良好.