基于压缩感知的菲涅尔孔径编码无透镜成像（特邀）

吴佳琛，曹良才

（清华大学精密仪器系精密测试技术及仪器国家重点实验室，北京 100084）

0 引言

基于透镜的成像系统通过设计光学镜组，将物空间发出的光线会聚到像空间，由像感器直接记录下物体的图像。为了提高成像质量，光学镜组通常采用多片透镜来校正像差，因此光学镜组占据成像系统大部分体积和重量，限制了成像系统的小型化和轻量化。基于编码掩膜的无透镜成像将具有特定图案的掩膜代替透镜置入成像系统内，入射光受到掩膜图案的调制，在像感器上形成编码图像，最后通过算法从编码图像中恢复出原始图像，相较于透镜成像系统具有结构简单、易于构建的特点。编码掩膜无透镜成像打破了物点到像点一一对应的成像方式，将成像的重心由硬件转移到算法上，并有可能进一步提取深度、波长等多维度的物体信息［1，2］。如何建立原始图像与编码图像之间的联系，并通过求解逆问题重建图像则是编码掩膜无透镜成像中的关键问题。

早期编码掩膜成像技术主要应用于高能射线成像中，也称为编码孔径成像。这是由于在高能射线波段中，各种材料的折射率都近似等于1，并有很高的吸收率，无法采用常规光学元件进行折射成像。而无需光学元件的小孔成像技术具有极低的通光量，需要长时间曝光才能获取清晰图像。1961 年，由MERTZ L 和YOUNG N 提出了波带片编码成像技术（Zone Plate Coded Imaging，ZPCI）［3］，用波带片代替透镜实现了编码成像。1968 年，DICKE R［4］和ABLES J［5］对小孔成像原理进行拓展，分别独立提出了用于X 射线和伽马射线成像的随机孔径阵列。之后FENIMORE E E 等提出的均匀冗余阵列（Uniformly Redundant Array，URA）［6］，以及GOTTESMAN S R 等提出的改进的均匀冗余阵列（Modified Uniformly Redundant Array，MURA）［7］已成功应用于工业伽马射线相机和高能天文望远镜系统［8］。这些方法主要基于几何光学模型，未充分考虑入射光透过掩膜版所产生的衍射效应。在可见光波段，由于波长和掩膜版图案特征尺寸相当，衍射效应不能被忽视，因而限制了其应用推广。为此，研究人员设计了各种类型的编码掩膜，如可分离掩膜［9-11］、散射屏［12，13］、菲涅尔波带片［14-16］等，并提出了相应的重建算法以提高成像系统的鲁棒性。

菲涅尔孔径编码成像技术将波带片编码成像技术拓展至可见光领域，其原理是利用菲涅尔波带片将目标物体编码成与同轴全息图具有相同形式的编码图像，因此可借鉴数字全息成像算法来重建图像。SHIMANO T 等提出采集至少四幅不同相位的波带片编码图像用来实现无孪生像的重建［14］。本文作者提出全变差正则化方法［15］和深度学习方法［16］实现了菲涅尔孔径编码成像的单次采集成像。菲涅尔孔径编码成像分辨率与波带片最外环宽度相当，而波带片最外环宽度随着菲涅尔波带片的半径增加而缩小，因此大幅面的像感器可以获得高分辨率的图像，但是对像感器成本提出了更高的要求。

为了在不损失图像分辨率的情况下降低硬件成本，可以使用多个小尺寸像感器来代替大尺寸像感器进行图像采集。由于多个像感器只能获得部分测量值，因此需要通过压缩感知技术来实现菲涅尔孔径（Fresnel Zone Aperture，FZA）编码成像。压缩感知是DONOHO D 等数学家于2006 年左右提出的一种新的信息获取指导理论［17-19］，能够通过稀疏采样，在远低于奈奎斯特采样频率条件下，通过寻找欠定线性系统稀疏解的方式，获得更好的图像重构效果。压缩采样技术已成功应用于磁共振成像［20］、相位恢复［21，22］、荧光显微［23］和全息成像［24，25］中。

本文基于全变差正则化重建算法，验证了FZA 编码成像系统在波带片常数小于某一阈值时具有压缩重建能力，提出一种基于部分采样的FZA 编码图像的压缩成像模型，能够实现在部分测量数据缺失的情况下重建高质量图像，并对不同采样数据量下重建图像质量进行了讨论，分别针对矩形采样和辐射线采样的两种数据采集方式进行了测试分析。

1 菲涅尔孔径编码成像模型

1.1 编码图像的记录

透光率连续变化的波带片被称为伽柏波带片（Gabor Zone Plate，GZP），其振幅传递函数可表示为

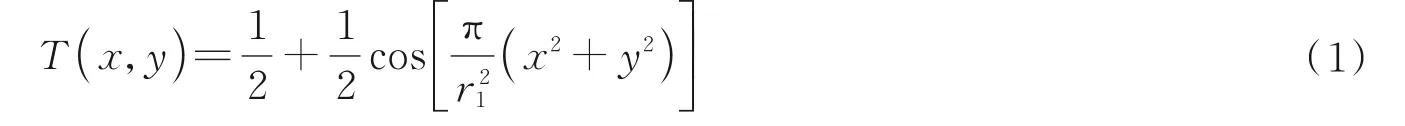
式中，(x，y)为空间坐标，r1为波带片常数，表示波带片最内圈环带的半径。但现有制造工艺难以加工正弦透过率型波带片。通常采用具有二值透过率的菲涅尔波带片（Fresnel Zone Plate，FZP）代替GZP 实现相应的功能。因为FZP 在编码掩膜成像中充当编码孔径的功能，也称之为菲涅尔孔径（FZA）。FZA 编码成像原理如图1 所示，物体到FZA 的距离为z1，FZA 到像感器距离为z2。物体受非相干光照明，其透射或反射的光线经FZA 调制后，由像感器记录下编码图像，最后利用优化算法计算重建出原始图像。

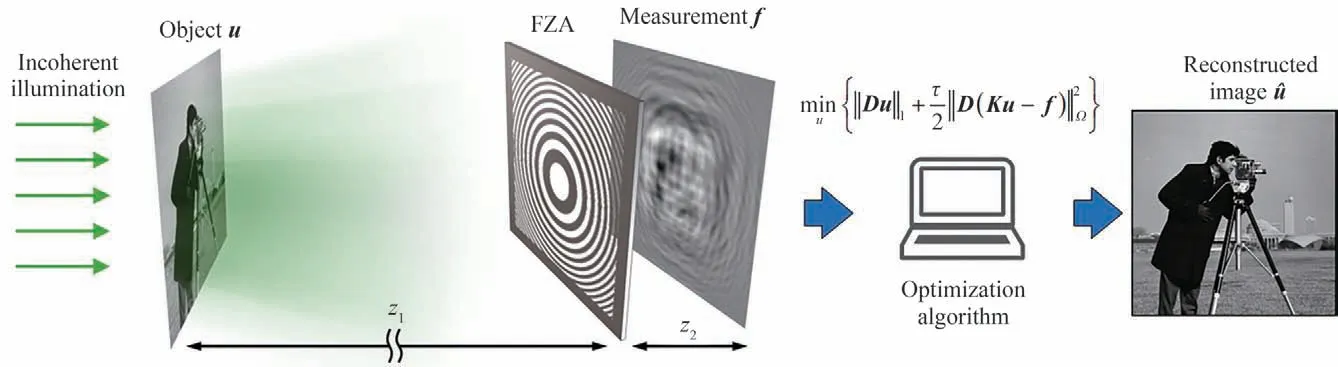
图1 FZA 编码成像示意图Fig.1 Principle diagram of FZA coded imaging

对于编码掩膜成像而言，像感器采集的图像可以表示为物体的像和掩膜版投影的卷积，即

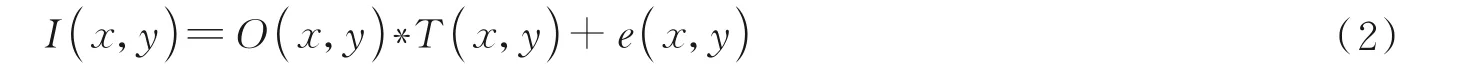
式中，符号*表示卷积算符；O(x，y)表示待复原的物体图像；T(x，y)表示掩膜版投影强度分布，当z1≫z2时，T(x，y)与掩膜版透过率函数等价；e(x，y)表示成像系统中各种因素引入的噪声，包括光电探测器噪声、环境光噪声，以及衍射效应引起的误差等。将T(x，y)中的余弦项用复指数的形式表达，即

1.2 反向传播重建

若要重建原始物体图像，可以数值模拟相干光对编码图像的衍射过程。采用角谱法计算衍射光场，可得重建光场的表达式为

2 菲涅尔孔径编码图像的压缩重建方法

2.1 压缩重建的RIP 条件

CANDÈS E 和TAO T 提出的约束等距性（Restricted Isometry Property，RIP）性质是判断传感矩阵能否实现信号压缩采样的一个重要标准［26］。RIP 性质的表达式为

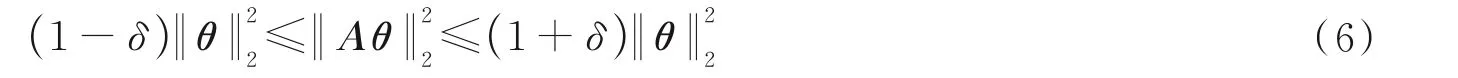
式中，θ为任意稀疏度为K的信号，δ为常数且δ∈(0，1)，A为传感矩阵。若传感矩阵A满足式（6），则可以称传感矩阵A满足RIP 性质，此时优化算法能够以高概率精确恢复原始信号。CANDÈS E 和TAO T 还证明了独立同分布的高斯随机测量矩阵可以成为普适的压缩感知传感矩阵［26］。但在实际中判断矩阵是否满足RIP 性质被证明是十分困难的［27］，而且RIP 只是一个矩阵是否可以作为观测矩阵的充分不必要条件，在实际应用中，人们更关心所设计的测量矩阵在能够准确恢复信号的条件下，所需的测量数量以及可以恢复的信号的稀疏度。因此，可将高斯随机测量矩阵对信号的恢复能力作为参照进行类比。本文采用正弦型波带片的一维径向函数对应的卷积矩阵作测量矩阵，对长度N= 2 048，稀疏度K= 200 的信号进行重构，用来验证菲涅尔孔径编码成像系统是否满足RIP 条件。模拟实验中分别测试了波带片常数为0.8 mm、0.7 mm、0.6 mm、0.5 mm 时的重构情况，信号和波带片的采样间隔为10 μm。其函数图像如图2（a）所示，信号重构结果如图2（b）所示，同时给出高斯随机传感矩阵作为参考。可以看到r1越小，重构误差越小，当r1= 0.5 mm时，重构性能与高斯随机传感矩阵几乎一致。即波带片常数越小，在压缩重建中对信号的重构误差也就越小。

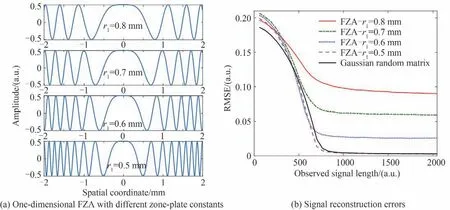
图2 FZA 传感矩阵与高斯随机传感矩阵对信号的恢复能力比较Fig.2 Comparison of signal recovery ability between FZA sensing matrix and Gaussian random sensing matrix

2.2 全变差正则化

通过构造优化目标函数实现编码图像的压缩重建。若以矩阵向量相乘的形式抽象出菲涅尔孔径编码成像的数学模型，则有

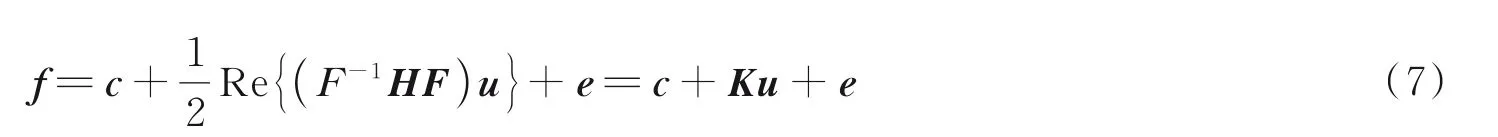
假设待复原图像的像素数为Nx×Ny=Nxy。其中u∈RNxy表示目标图像，f∈RNxy表示编码图像，c和e分别表示常数和噪声，F∈CNxy×Nxy表示二维傅里叶变换矩阵，F-1∈CNxy×Nxy则是对应的逆傅里叶变换矩阵；H∈CNxy×Nxy是对角矩阵，其对角线上的元素是菲涅尔衍射传递函数的离散采样值；Re{·}表示取实部操作；K算子则是结合了F-1HF以及取实部操作，代表了整个成像系统的前向模型。在菲涅尔孔径编码成像应用中，物函数u始终为实函数，且菲涅尔衍射传递函数H为径向对称函数，则Re{(F-1HF)u}等价于(F-1Re{H}F)u，即K算子为线性算子，因此可以用线性回归模型相关的优化算法对原始图像进行求解。

由于孪生像和原始像以及二者之和都能满足式（7），因此图像重建具有多个解，属于不适定性问题，需要施加正则化项使解保持唯一且稳定。孪生像本质上是原始图像的离焦图像，聚焦图像的边缘清晰锐利，边缘以外的区域则过渡平滑，而离焦图像在图像边缘会产生衍射条纹，并且衍射条纹随着传播距离增大扩散到整个图像。反映在图像的梯度上，聚焦图像的梯度大部分趋于零值，呈现稀疏性，而离焦图像则是非稀疏的。所以聚焦图像的全变差要比离焦图像的全变差小得多。图3 给出了离焦图像和聚焦图像梯度域的图像及相应的直方图分布，其中聚焦图像在梯度域具有明显的稀疏特性。因此，可以采用全变差正则化实现抑制孪生像的效果，全变差正则化项可写为

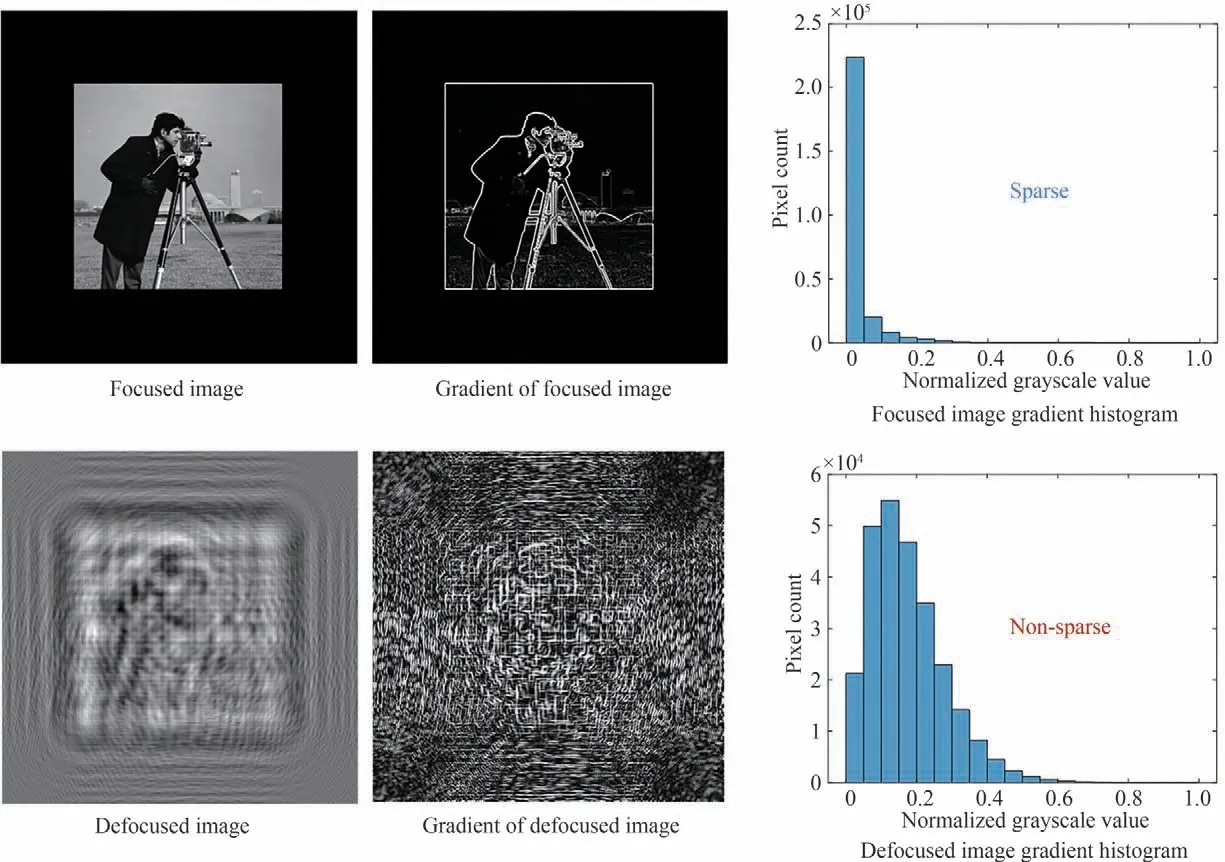
图3 聚焦图像和离焦图像的梯度域稀疏性比较Fig.3 Comparison of sparsity in gradient domain between focused and defocused images

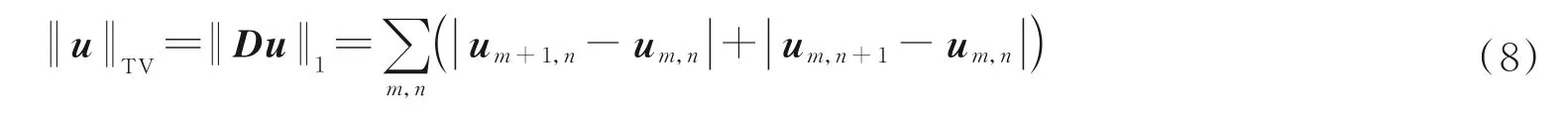
式中，D表示差分算子，m、n表示二维离散图像的像素索引。

2.3 优化目标函数

根据上述分析，设计如下优化目标函数

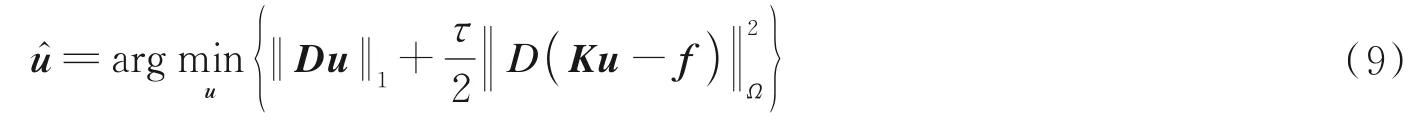
式中，Ω表示采样区域的指标集，‖ ·‖Ω表示在仅在指标集Ω上计算l2范数，τ＞0 为正则化参数。值得注意的是，在误差项Ku-f前添加一个差分算子D，能够有效消除编码图像中常数项的干扰，提高成像质量。

式（9）可以通过交替方向乘子法（Alternating Direction Method of Multipliers，ADMM）进行求解。ADMM 方法可将复杂的问题分解成若干个易于求解的子问题，缩小了问题的规模，降低了求解难度。首先将式（9）改写为等价的约束优化问题，即

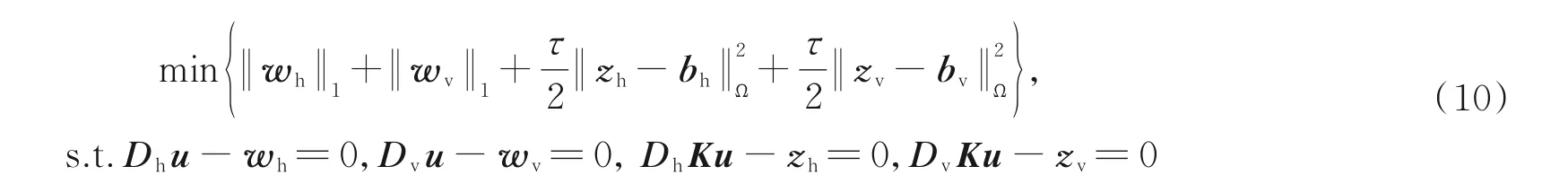
式中，Dh和Dv分别为水平方向和垂直方向的差分算子，bh=Dhf，bv=Dvf。该问题的增广拉格朗日函数定义为

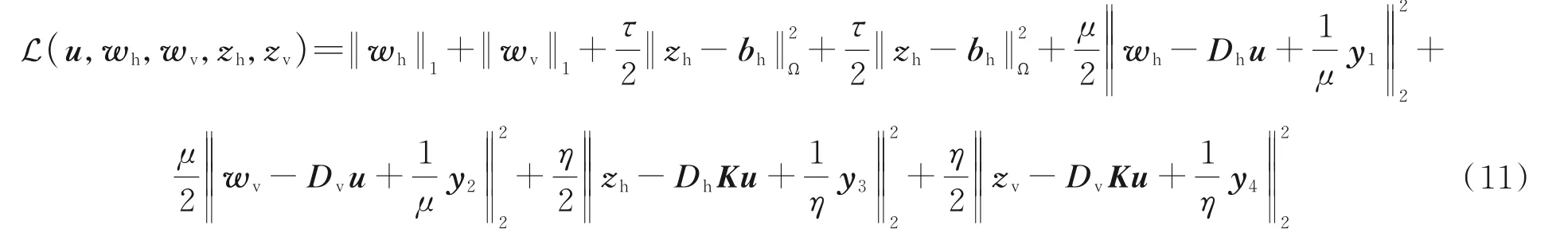
式中，y1、y2、y3、y4为尺度对偶变量，μ＞0、η＞0 为惩罚参数。通过给定中间变量wh、wv、zh、zv和尺度对偶变量y1、y2、y3、y4的初值，ADMM 算法在第k次迭代过程中依次求解如下子优化问题

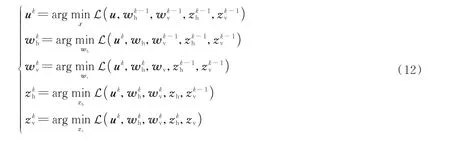
并更新对偶变量

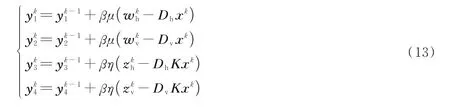
式中，β∈(0，( 5 +1) 2 )用来控制更新的步长。通过交替迭代优化u、wh、wv、zh、zv、y1、y2、y3、y4最终恢复原始图像u。

3 重建结果与分析

3.1 数值重建结果

在数值模拟实验中，原始图像尺寸为256×256 像素，像素间隔为10 μm；掩膜版图案为菲涅尔波带片，波带片常数为0.25 mm，掩膜版尺寸为512×512 像素；完整的编码图像尺寸为768×768 像素。取完整编码图像中心的256×256 像素部分作为像感器所采集的图像，现根据该采集图像，通过减少该采集图像的数据量，测试压缩重建算法对原始图像恢复的性能。首先采用矩形采样区域对编码图像进行采样，采样比例以256×256 像素的采集图像作为100%的测量数据进行计算。由于重建图像的像素值分布范围与原图不尽相同，因此采用相关系数（Correlation Coefficient，CC）对重建图像质量进行评价。对于两幅图像A和B，相关系数定义为

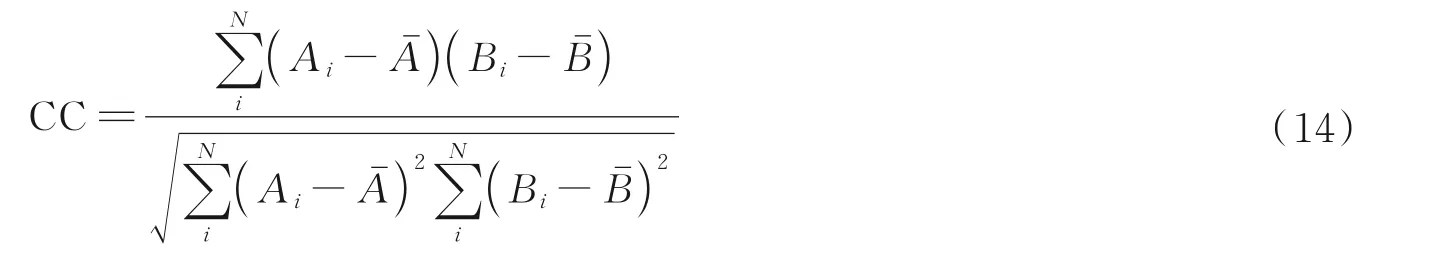
为了进一步分析采样数据量对重建图像质量之间的相关性，对分类主观图像质量（Categorical Subjective Image Quality，CSIQ）数据库［28］中30 幅图像进行测试，每幅图像均采用ADMM 算法迭代200 次，最终重建图像的相关系数分布如图4（c）所示。图中箱线图框内的线条表示样本中位数，框的下边缘和上边缘分别表示下四分位数和上四分位数，即数据从小到大排序后处于25%和75%位置上的值，二者之差为四分位距（Inter-Quartile Range，IQR）。圆圈表示离群值，即超出上下四分位数1.5 倍IQR 的值，竖线的上下两端分别表示除去离群值之后的最大值和最小值。最后用折线图连接了每种采样数据量下相关系数的均值，当采样数据量小于50%，图像重建质量随着采样数据量的减少而迅速下降，在采样数据量仅为6.3%的情况下，重建图像相关系数均值降至0.30。

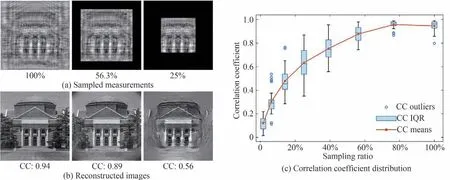
图4 基于矩形采样区域的压缩重建结果Fig.4 Compressive reconstruction results based on rectangular sampling area

实际上，矩形采样并没有充分考虑编码图像在频谱域中的能量分布情况。由于像感器对斜入射光线不敏感，实际视场角被限制在小范围内，也就是波带片投影的位移远小于波带片的直径，此时，像感器的各个像素接收到光强仅来自于波带片投影对应的局部小区域的叠加，因此，编码图像整体上呈现和波带片类似的频率分布，其特点为图像中心低频成分居多，图像边缘高频成分居多。矩形采样只对图像中心部分进行采样，会导致重建图像的高频信息缺失而变得模糊不清。随着衍射距离的增大，菲涅尔衍射图像逐渐向夫琅禾费衍射图像转变，而夫琅禾费衍射图像和原始图像的频谱分布具有相同的形式［29］，因此，菲涅尔衍射图像处于空域图像向频谱图像转化的中间状态，与原始图像的频谱能量分布具有一定相似性。由于大多数自然图像的频谱能量都集中在低频，所以应该在靠近中心的地方进行更密集的采样，以匹配能量分布。采用如图5（a）所示辐射线采样图案，辐射线由图像中心向外发散，并均匀遍布整幅图像，辐射线数量从左到右分别为64、48、32，相应的采样数据量分别为完整编码图像的13.9%、10.7%、7.3%。这种采样方式可以保证中心和边缘的图像信息都能被采集到，并且在图像中心处得到更多的采样数据，可通过线阵相机来实现。类似的采样方案已应用于相位恢复［21］、计算机断层扫描［30］、核磁共振成像［31］等领域。相对于矩形采样而言，辐射线采样能够以更少的采样数据量重建出高质量的图像。如图5（b）所示，辐射线采样仅用10.7%的采样数据重建的图像与矩形采样使用56.3%的采样数据重建的图像有相同水平的重建质量，重建图像相关系数均为0.89。从图5（c）中也可看出，基于辐射线采样的图像重建质量随着采样数据量的减少下降缓慢，即使在采样数据量仅为5.7%的极端情况下，重建图像相关系数均值仍有0.77。

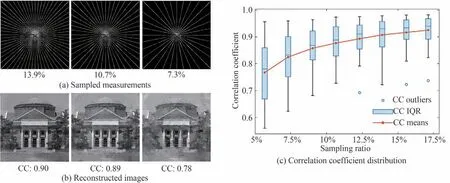
图5 基于辐射线采样区域的压缩重建结果Fig.5 Compressive reconstruction results based on radial line sampling area

3.2 实验重建结果

实验中采用液晶显示屏（Liquid Crystal Display，LCD）显示待成像的图像，LCD 被放置在距离无透镜相机约30 cm 的地方。目标图像为一含有“HOLOLAB”字样的矩形标志，其显示在屏幕中的尺寸为130 mm×140 mm。无透镜相机所采用像感器为QHY163M，像素间隔为3.75 μm。菲涅尔波带片放置在距离像感器3 mm 处，取其中心2 048×2 048 像素作为采集到的完整的编码图像。分别使用完整的编码图像和不同采样模式进行图像重建。使用图6（a）中的采样模式对测量数据进行重建，对应的重建结果如图6（b）所示，所展示的图像为重建图像中心500×500 像素部分。结果表明，在采集数据量仅为7.3%的情况下，该方法仍能有效识别出字母。通过图6（c）字母“O”的横截面强度可以看出，在三种不同采样模式下，图像对比度并未见明显下降，验证了该方法具有良好的图像边缘保持特性。矩形采样模式可由多块小尺寸面阵像感器拼接实现，辐射线采样模式可由单个线阵像感器多次旋转采集，或者采用多个线阵像感器拼接实现。考虑到实际装配的可行性，也可采用中心放置面阵像感器，周围放置线阵像感器的混合排布方式，并对装配完成后像感器阵列进行一次标定，减小装配误差对图像重建的影响。

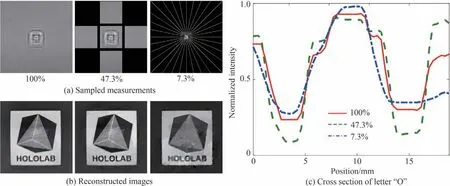
图6 实验测量图像的压缩重建结果Fig.6 Compressive reconstruction results of experimental measurement images

4 结论

本文提出了一种用于菲涅尔孔径编码成像的压缩采样方法，构建了从不完全测量中恢复原始图像的压缩重建模型。分析了菲涅尔孔径编码压缩采样模型的不相关特性，比较了菲涅尔孔径编码的测量矩阵和随机高斯测量矩阵对信号的恢复能力，验证了一维情况下波带片常数小于0.5 mm 时，重构性能与高斯测量矩阵几乎一致。提出并推导了基于ADMM 的压缩重建方法，对不同采样数据量下的矩形采样模式和辐射线采样模式进行了定量分析，验证了辐射线采样模式相比矩形采样模式具有更高的图像采样效率。实验表明，该方法仅通过7.3%的测量数据就可以获得质量良好的图像，可以用于菲涅尔孔径编码像感器阵列成像。所提出的方法能够在保持重建图像质量的同时，大幅降低测量数据，验证了基于菲涅尔孔径编码成像构建多像感器架构的可行性。