新冠肺炎传播预测优化:基于少量早期数据的多阶段SEIRr模型

2022-08-29谭索怡欧朝敏

预测 2022年4期

赛斌, 宋兵, 谭索怡, 欧朝敏, 周涛, 张伟, 吕欣

(1.国防科技大学系统工程学院,湖南长沙 410073; 2.电子科技大学大数据研究中心,四川成都 611731; 3.四川大学华西医院华西生物医学大数据中心,四川成都 610041)

1 引言

2019年12月8日，湖北省武汉市发现不明原因引起的肺炎，后被证实该疾病由新型冠状病毒(SARSCoV-2)引起，2020年2月12日世界卫生组织(WHO)将由这一类病毒引起的疾病命名为COVID-19。与SARS不同，COVID-19潜伏期具有一定的传染性，并且存在大量无症状感染者，这给疫情防控工作带来了巨大挑战。截至2022年6月10日，全球COVID-19感染人数已超5.117亿例，累计死亡人数超632.8万，众多国家的社会和经济因此遭受了巨大损害，人类社会也因此面临着前所未有的挑战。当前我国疫情处于平稳态势，但仍存在着反弹风险，坚持“外防输入，内防反弹”的总策略，减少疫情对社会各方面的影响，研究如何根据疫情形势制定防疫措施具有重要意义。在面对突发传染病时，掌握疫情发展态势，合理有效的防疫政策能够控制疫情发展，将影响降到最低，也能够最大程度地保障社会各方面的正常运转。由此可见，准确合理地预测传染病发展趋势，提前规划应对措施或制定防控策略，才能最大化地实现“动态清零”策略。

自疫情暴发以来，基于传染病传播动力学模型分析与预测COVID-19的传播特征及发展趋势成为了研究人员的主流研究方法。在疫情发生初期，Wu等通过使用中国疾病预防控制中心发布的2019年12月31日到2020年1月28日期间医学统计数据，结合官方航空指南的每月航班预订数量与腾讯位置大数据得到的人口流动数据构建SEIR模型，估计得到COVID-19的基本再生数为2.68(95%Crl 2.47～2.86)，疫情倍增时间为6.4天，推断COVID-19在中国内地主要城市的感染人数将呈现指数增长并预测武汉市将在2020年1月25日会有75815位新冠肺炎感染患者。Zhou等基于2020年1月25日前的已有的医学统计数据及国际同行估计的感染人数，参考SARS流行病的参数构建SEIR模型估计COVID-19基本再生数，得出COVID-19基本再生数在2.9～3.2之间的结论。Shen等基于新冠疫情的传播机制，考虑了防控措施，建立传染病传播动力学模型，预测出COVID-19暴发规模将在2020年2月5日到达峰值。Tang等基于似然估计和模型仿真的估计结果表明，武汉市的控制繁殖数可能高达6.47(95%CI 5.71～7.23)，该文章也预测了在最严格的管控措施下，中国内地将于2020年1月23日起的两周内达到疫情峰值最小。王聪等利用文献统计的最新流行病学数据估计疫情早期基本再生数，结果显示武汉市在2020年1月21日前后的传染病参数

为2.55(95%CI 2.55～2.65)。

可见，基于病理学的传染病传播动力学模型的COVID-19基本参数信息分析与疫情发展态势预测研究对新冠肺炎流行因素的掌握以及防控策略和措施的制定具有重要作用，并且对于早期疫情的控制具有指导性作用。随着互联网及大数据等技术的迅猛发展，也有学者将SEIR模型结合人口迁徙网络或机器学习等方法研究传染病的传播机制，例如，Yang等基于对潜伏期患者具有感染性的考虑优化了SEIR模型，并结合LSTM深度学习方法进行建模，预测得到中国内地的疫情规模将于2020年2月28日到达顶峰，然后在4月底逐渐平缓。Jia等利用手机定位大数据分析人口流动时空特征，然后基于疫情暴发前武汉输入到全国各地的人口流动数据，构建了“时空风险源模型”，该模型最多可以提前两周预测出新冠疫情暴发的时间、强度和地理分布。谭索怡等对北京市COVID-19的密切接触者进行数据分析时发现，新增密切接触者的增长率与5～6天后的新增确诊病例增长率变化趋势一致，由此推断中国内地新增确诊人数在2020年2月13日左右开始出现下行。但是，由于在疫情暴发初期医学检测能力不足,以及对新型冠状病毒肺炎传播机制、传播能力认知的不足，导致了研究人员在进行COVID-19疫情动力学建模研究时缺乏足够的医学统计数据以及对新冠肺炎传播机制的错误认识，因此难以准确估计疫情发展态势。

随着COVID-19相关特性研究的不断深入，有研究表明COVID-19的潜伏期患者也具有感染性，并且存在无症状感染者，而大量已有的建模预测研究忽略了这些特征。所以，考虑到各种实际情况时，一般都需要在传统SEIR模型上进行必要的修改以贴合新冠肺炎实际传播情况，例如，北大统计学团队的Yan等细分人群种类建立vSIADR模型估计有效再生数并对各国疫情进行波次划分，研究了25个国家的控制措施对COVID-19传播的效果；López和Rodo等改进SEIR模型建立了SEIQRDC模型解释了潜伏期的感染传播情况。魏永越等开发SEIR(+CAQ)动态模型较为准确地预测了中国内地主要疫区的累计确诊病例数。然而，由于没有全面考虑到疫情传播特征与机制以及对疾病的认识的动态变化造成的防控、诊断及治疗的优化等问题，以上研究方法存在或预测准确率低，或没有全面考虑COVID-19传播特征，或用于拟合数据多、预测周期短等问题。因此，在面对重大新发突发传染病时，构建更为合理的传播动力学模型，采用多阶段建模方法预测疫情发展趋势并分析传染病传播机制势在必行，这将有利于相关部门制定更为科学合理的防控措施,各地医疗卫生机构提前做好应急准备工作，有效提升疫情防控效率。

为解决上述问题，本文在综合考虑COVID-19的传播特性的基础上，构建了多阶段SEIRr模型预测COVID-19传播趋势，并基于国内外不同阶段真实医学统计数据进行实证分析，验证了模型的有效性、可靠性及普适性。其主要创新点如下：(1)充分考虑了COVID-19传播特性，即潜伏期患者传染性与自治愈等特点，增强了传染病传播动力学模型的稳健性。(2)创新性地应用了梯度下降算法进行参数估计，提升了传播动力学模型参数估计的有效性。(3)增加了对模型输入初始医学统计数据初始值的估计，降低了模型对前期数据的质量要求。本文提出的方法和模型具有很好的可解释性，可以为相关部门制定科学合理的疫情防控措施提供一定的理论支撑。

2 模型与仿真

2.1 SEIRr模型建模

经典的SEIR模型将人群分为了

(易感者，未感染但存在感染风险人群)、

(潜伏者，感染但不不具有传染性的未发病状人群)、

(感染者,已发病的具有传染性人群)以及

(康复者，指病愈或因病死亡人群)4类。然而，据现有研究表明：COVID-19的潜伏期人群具有传染性，且由于疫情初期检测力度不足导致部分无症状患者和自治愈人群被选择性忽略了；另外，现实情况下并不是每个人与病毒携带者接触后就一定会被感染。因此，

类人群中存在一定比例的无症状感染者、自治愈人群以及无效接触者，他们将直接从潜伏期人群中移除出去。

(1)

根据此次COVID-19疫情的特征，本文做出如下假设:

(1)假设考察地区的人口总量

不变，即不考虑人群生死及迁移等种群动力因素。

(2)假设考察期间，病毒不发生变异，疫情防控政策维持相对稳定，即保证传染率不发生变化。

(3)假设COVID-19的传染率为

，则在

时刻单位时间内被感染者感染的人数为

(

)

(

)

(

)。(4)考虑潜伏期人群具有传染能力，其传染能力为感染者的

倍(

<1)。(5)假设

与病毒携带者接触后可以转变为无症状、无效接触、自治愈和感染但未被确诊四类人群中的一种，其中前三类人群将以速率

从

中移除成为

类，感染未确诊人群将以速率

转为感染者

，最终被移除成为

类。则在

时刻由感染者转为康复者的人数

(

);由潜伏者转为移除者的人数

(

)。

基于以上假设，本文构建了考虑疫情防控措施影响的SEIR模型——SEIRr模型，图1为SEIRr模型的示意图。模型的微分方程表达式如公式(1)所示，微分方程中的各个参数的取值参考及其具体含义参照表1。

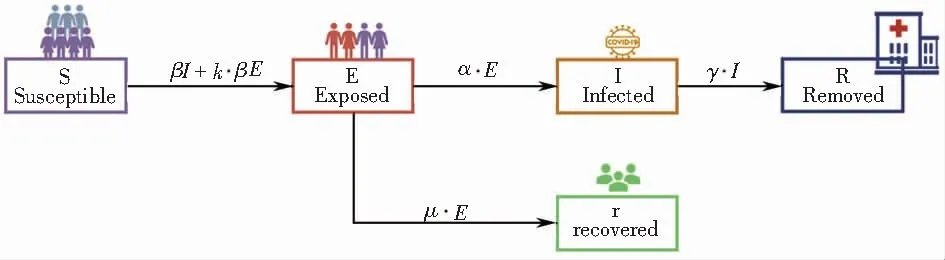
图1 SEIRr模型示意图

2.2 参数设计与估计方法

利用传染病传播模型进行仿真预测的必要前提是得到有效的参数值，在本模型中需要求解的参数包括

、

。由于

和

分别是潜伏期患者发病速率(平均潜伏时长

的倒数)与平均康复速率(平均治愈时长

的倒数)，二者受医疗资源与诊疗水平限制，本文假设短时间内二者为常量。据Li等，Guan等估计，

与

分别约为5.4天与13天，故

5.4，

13。因此，待估参数还有

、

。此外，为进一步提高SEIRr模型的预测效果，本文在估计上述未知参数的同时通过梯度下降算法自动调整微分方程输入初始值

(0)、

(0)，从而有效克服因疫情暴发初期对新发传染病认知不足造成的数据统计偏差和数据不足等问题。

为有效、准确估计模型参数，本文采用批量梯度下降算法进行参数估计，各参数值在梯度下降算法拟合优化过程中损失函数最小时取得。梯度下降算法的损失函数如下

(2)

其中代表实际值与预测值间的均方误差为L2正则项(可以有效避免过拟合问题)，

代表

等待拟合参数。

3 实证分析

3.1 数据来源

本文所采用的用于模型拟合与预测的真实医学统计数据包含国内和国外两部分。其中国内数据获取于中国国家卫生健康委员会官方网站及各地方卫生健康委员会官方网站的每日疫情通报数据，国外数据主要来源于美国霍普金斯统计的各国每日累计确诊人数、累计死亡人数以及累计治愈人数等流行病学数据。由于本文研究模型的假设条件之一为传播环境稳定，故武汉数据取2020年1月23日宣布“封城”以后进行研究，其他疫区的医学统计数据均取自于2020年1月24日全国各地实施公共卫生安全一级响应措施以后。同理，本文所研究的国外的医学统计数据也均取自于传染病传播环境相对稳定之后的数据。用于模型拟合的数据为疫情前期10天左右的每日现有确诊人数，其余数据用于检验模型拟合效果。

3.2 武汉疫情预测分析

首先，考虑到疫情初期病毒检测水平的不足而造成确诊病例数堆积，2020年2月12日中国卫生健康委员会首次将临床诊断病例纳入统计导致武汉市当天累计确诊人数激增，这使得武汉市在该日前后两天统计数据出现明显断层。为消除数据问题造成的预测偏差，本文对2020年2月12日新增加的临床诊断病例进行平均平滑处理，将其平均分配到1月23日至2月12日期间，图2a为数据处理前后的对比图。然后，我们利用梯度下降算法迭代运算5000次对平滑处理后得到的每日确诊人数进行拟合，估计相应的传播动力学参数。SEIRr模型参数初始值设定以及通过批量梯度下降算法拟合得到的结果如表1所示。

表1 武汉市SEIRr模型参数设置详情

详情参数含义初始值参数设置依据拟合结果MCMC抽样N舱室中的接触人数2000000文献[28]2001272-S(0)初始易感染人群1997455S=N-E-I-R1998364-E(0)初始潜伏期人群1500估计值1502-I(0)初始感染人群991湖北省卫健委数据再平滑处理1349-R(0)初始移除类人群(包括治愈与死亡)54湖北省卫健委数据57-β易感者与感染者的接触速率4.5按经验随机取值4.3081.023kk·β表示易感者与潜伏期人群的接触速率1按经验随机取值0.2020.015μ潜伏期人群中的无效接触、无症状感染、自治愈人群转化为r的速率2.9按经验随机取值3.2360.079α潜伏期人群被检测为感染者的检测速率1/5.4文献[22,23]1/5.41/5.4γ感染者被治愈速率1/13文献[23]1/131/13

武汉市现有确诊人数的预测如图2b所示，图中绿色圆圈为参数拟合用数据，其余真实数据(黑色圆圈)作为对比评价SEIRr模型预测效果，最终得到了

=0.975的拟合优度。从拟合得到的结果可见：①武汉市每日现有确诊人数的预测结果与实际基本符合；②潜伏期人群相较于感染期人群的传染率不高，约为感染者的20

左右，这与中国-世界卫生组织新型冠状病毒肺炎(COVID-19)联合考察报告所描述的“感染者在出现症状前1～2天才能检测到核酸病毒判断潜伏期患者在出现症状1～2天才具有传染性”的研究是相吻合的；③从图2c可以看出后期治愈速率是大于1

13的，从而导致疫情进度存在10天左右的滞后，这与医疗资源与诊疗手段的更新相关。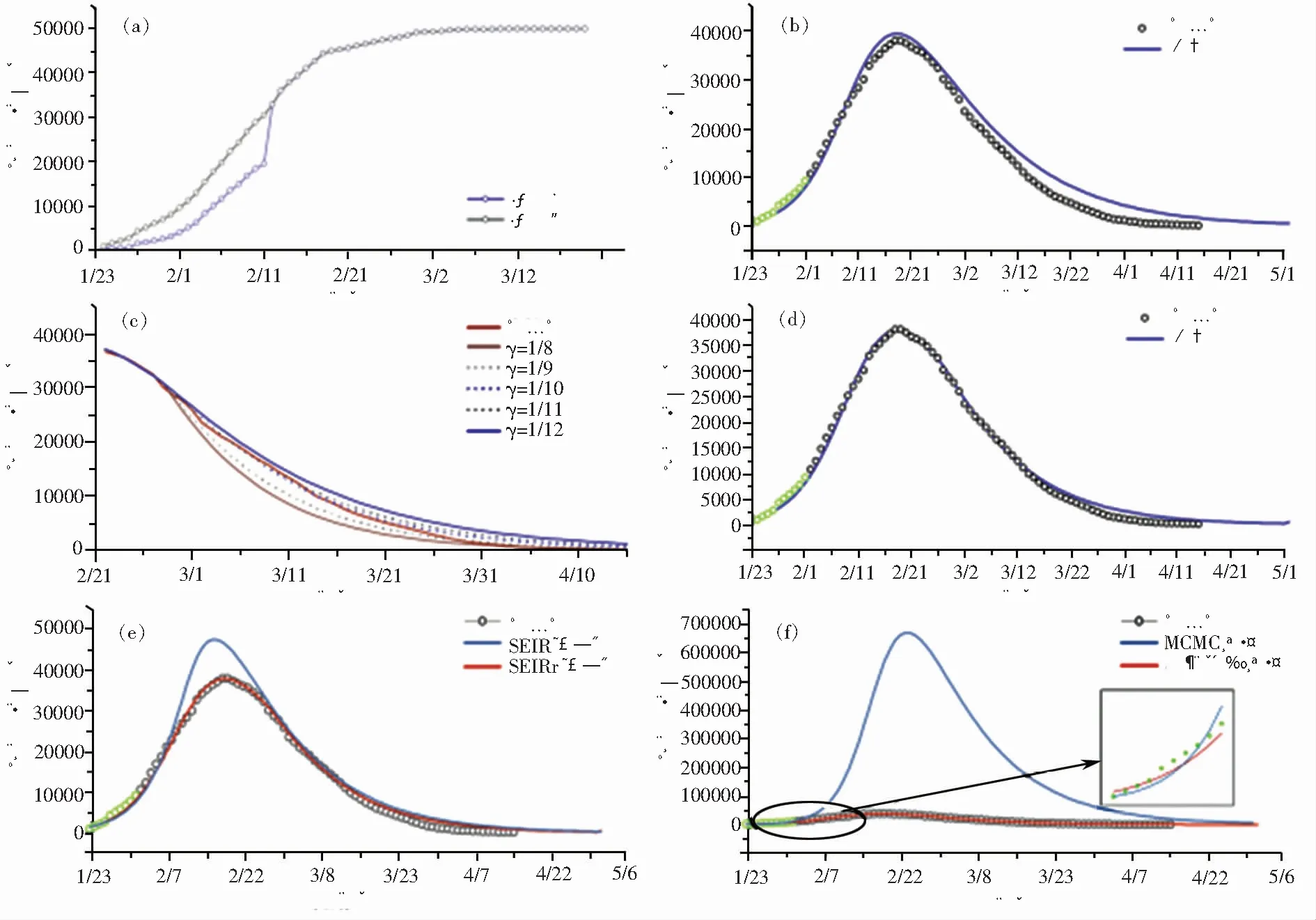

图2 武汉市疫情预测

从结论③中可以看出，随着各界对COVID-19认知水平的提高，武汉市针对COVID-19的诊断与治疗效果存在显著提升，然而在新冠肺炎暴发初期发表的论文基本都忽略了该因素对COVID-19发展态势的影响，这也导致其预测COVID-19的发展趋势与实际情况存在较大的偏差。本文考虑改变后期(2020年2月27日以后)参数进行仿真模拟预测疫情发展态势以验证我们的推测，当后期治愈速率更新为1

10时的预测效果最佳，其拟合优度提升到

=0.996,和图2d所示。为进一步验证SEIRr模型的预测效果和批量梯度下降算法可靠性，本文使用控制变量法进行了必要的对比试验。首先进行了马尔科夫蒙特卡洛方法(MCMC)和批量梯度下降算法的参数估计效果对比实验：为保证与批量梯度下降算法参数一致，MCMC确定模型输入初始值以及参数

和

与梯度下降算法一致的基础上，使用了8000次NUTS采样，最终确定

、

三个参数值，预测值如表1所示。结果表明，与批量梯度下降相比，MCMC仅能估计三个参数，且估计精度与抽样次数相关，抽样次数越多则精度越高；估计参数的预测效果如图2(f)所示，批量梯度下降方法的结果显然优于MCMC方法。然后是SEIR和SEIRr的模型预测效果对比实验：在该实验中两模型的参数估计方法均采用批量梯度下降算法迭代运算5000次对武汉市1月23日至3月2日期间的每日确诊人数进行拟合并得到模型参数，然后将参数代入相应模型进行仿真实验，预测效果如图2(e)所示。结果表明，SEIR模型存在疫情峰值时间预测偏早，疫情峰值偏高等问题，SEIRr模型预测效果显然比传统SEIR模型更好。

3.3 国内主要地区疫情预测

为了验证模型的普适性，本文用同样的方法对国内的广东、河南、湖南、重庆、浙江等地区在2020年1月24日至2020年2月3日期间，以及上海在2022年3月11日至2022年6月10日期间每日现有确诊人数进行拟合，从而得到相应的传染病传播动力学方程的参数。与2020年原始新冠病毒特性不同的是，此轮上海疫情是由变异毒株——“奥密克戎”引起，据复旦大学研究成果表明，其平均潜伏期时长和在院治疗时长分别为1.2天和5.6天。因此，上海疫区的参数

与

分别设置为1

1.2和1

5.6。通过仿真预测得到的结果如图3中的红色实线所示，各地区拟合优度也都在90

以上，与武汉市情况类似，国内其他地区的后期治愈速率同样得到了提升，治愈速率更新后的拟合效果如图3中的蓝色实线所示(其中2022年上海疫情仅用单阶段模型即可得到相对准确可靠的拟合结果)。这表明，在传染病传播环境稳定的条件下，SEIRr模型的预测精度和准确性具有可靠性；随着人们对病毒认识的提高和诊疗水平的提升，使得COVID-19患者的平均治愈速率能够提升并维持相对稳定。

图3 中国主要地区疫情发展趋势预测

3.4 国外疫情趋势拟合与预测

为了进一步验证模型的普适性，本文挑选了传染病传播环境都是较为稳定的意大利、德国、日本、瑞士四个国外疫区疫情发展趋势进行预测。其中意大利和德国均采取了类似于中国的封城措施，意大利在2020年3月4日宣布全国学校停课，3月8日实施“封城”措施，德国则是在3月16日由总理默克尔正式宣布实施“紧急防疫措施”。而日本则是在4月7日实行“软封城”措施，该措施更多地是依靠居民的自觉性。瑞士实行的是“群体免疫政策”，政府没有采取任何强制措施对COVID-19进行限制。

使用同样的方法对国外数据进行参数估计并预测疫情发展趋势，参数设置与预测结果如表2与图4所示。实验结果显示，各国实际与预测每日现存确诊人数之间的拟合优度均在0.97以上。这表明，基于前期的公布的少量医学统计数据，利用梯度下降算法对SEIRr模型求解，也可以有效预测国外疫情发展趋势。

表2 国外疫情SEIRr模型拟合结果

国家βkμ第一阶段α第二阶段α第一阶段γ第二阶段γ德国3.6320.6954.2131/5.41/5.41/141/14日本3.3570.03033.1081/5.41/5.41/141/14意大利3.0250.4163.0171/121/101/151/13瑞士4.7660.4123.0861/101/81/161/13

进一步，本文对比了上述四个国家拟合所得的传播动力学模型参数。可以看出，实施“群体免疫”政策的瑞士传染率最高；而意大利的防控措施效果较好，其传染率是所有国家中最低的；德国和日本的传染率较为相近；意大利与瑞士的检测速率与治愈速率均较小，本文推断这是由于意大利感染人数较多所致，瑞士则是因为实行“群体免疫”政策而导致的检测水平滞后，康复周期变长；但两参数值在第二阶段是有增大的，这进一步佐证了“随着对疾病认知的提高，医疗资源也必将得到优化”的观点。

图4d为意大利疫情趋势预测结果，该结果所用的拟合数据为3月21至4月5日之间的每日现有确诊人数。为说明使用近期数据能够更好地预测疫情发展的变化趋势，本文使用不同时期的数据对意大利疫情趋势进行预测，其结果如图5所示。由图5可见，随着参数学习所用的医学统计病例数所处时间段的推移，SEIRr模型预测准确率不断提升；从总体上来看，前期预测结果较实际医学统计数据高但各时间段所推测出的疫情峰值与实际日期均高度重合。这有可能是由于意大利在疫情初期存在检测力度不足而导致前期公布的每日现有确诊人数偏低。

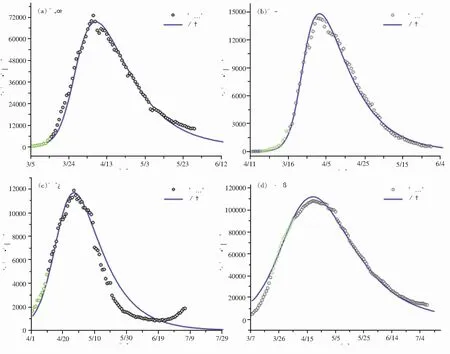
图4 国外部分国家疫情发展趋势预测

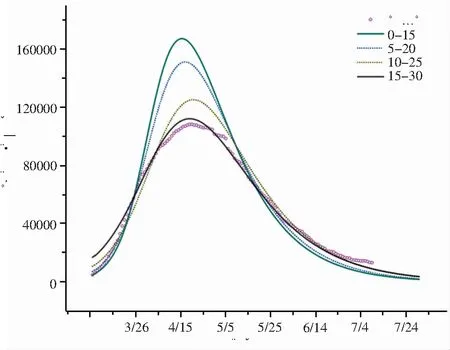
图5 不同拟合数据下的意大利疫情预测结果

4 结论与展望

本文结合COVID-19传播特征提出了一种考虑潜伏期患者传染性、感染期人群自治愈能力、无症状感染者以及无效接触人群的SEIRr模型。模型基于疫情早期少量医学统计数据，使用批量梯度下降算法估计传播动力学参数及初始感染人数从而预测疫情发展趋势。研究得到以下的结论：(1)本文的各项实验结果表明，通过估计模型初始值可以有效克服因早期医学统计数据误差以及对传播特征的错误理解等原因而造成预测偏差问题。(2)相较于传统SEIR模型，SEIRr模型假设更贴合COVID-19实际传播情况，实现了对国内外多个地区的疫情发展趋势的精准预测，其拟合优度提高到了0.95以上。(3)相较于基于统计学的MCMC抽样的参数估计方法，梯度下降算法具有更好的拟合效果，能够为其他传播动力学参数估计提供有效借鉴。

基于本文相关研究结果，得到的传染病防控管理启示有：(1)从源头抓起，坚决管制隔离病毒携带者和密切接触者，防止疫情扩散。(2)降低传播率

，舆论引导民众做好个人防护措施，政府加大监管力度，切断病毒传播途径。(3)提高参数

的值，在条件允许的情况下，适当增加核酸检测强度，及时发现病毒携带者，尽早隔离。(4)提高治愈速率

，加大相关科研的投入，研发疫苗和治疗药物，提升医疗资源配置，以应对大规模的疫情反弹风险。