显著特征的标记图像倾斜校正方法研究

高 聪

（黄河水利职业技术学院，河南 开封 475000）

0 引 言

图像倾斜校正是数字图像处理技术中的重要处理方法，用途极为广泛。随着对工业生产效率和产品质量检测要求的提高，对数字图像处理的计算速度和检测精度提出了新的挑战。针对这一难题，提出一种具有显著特征图像的倾斜校正算法。

本课题图像倾斜校正算法采用“显著特征的标记图像十字线”设计方案。该方案以标记图像十字线为图像处理核心，并给出具体倾斜校正算法和处理方法。在标记图像处理过程中，首先通过直线拟合获取标记图像的倾斜角度。其次，根据标记图像的特征对倾斜校正算法进行研究。最后，对图像插值方法进行优化。该图像倾斜校正算法具有较高的计算速度和检测精度，适用于对工业产品表面质量检测有较高速度和精度要求的领域。

1 标记图像直线拟合

1.1 直线拟合与角度获取

在标记图像采集过程中，由于受工业生产环境的影响，难免对标记图像的采集造成不同程度的倾斜。在对标记图像进行倾斜校正的处理过程中，首先要获取标记图像的倾斜角度。获取倾斜角度的方式主要采用标记图像边缘点直线拟合。标记图像是具有显著特征的十字线标记。为提高检测速度和检测精度，采用霍夫变换算法对标记图像进行直线拟合，以获取倾斜角度。

霍夫变换将图像像素空间变换到参数空间进行处理。通过在参数空间检测特征点进行直线拟合。

霍夫变换的基本算法：假设(x,y)是直角坐标系中的一个坐标点，经过该坐标点的直线有无数条。经过该坐标点的直线均符合公式（1）：

式中：为斜率；为截距。对式（1）进行变换得到式（2）：

式中，将，作为新的参数向量，建立新的坐标系。该方程的斜率和截距分别定义为x，y。将该方程转换为参数空间后如图1所示。假设(x,y)是直角坐标系中的一点，则该点映射为霍夫变换空间中的一条直线=-xa+y。同理，(x,y)是直角坐标系中的另一点，则该点映射为霍夫变换空间中的另一条直线=-xa+y。反之，经过坐标点(x,y)和(x,y)的直线对应霍夫变换空间一点(,)。在霍夫变换空间中的两条直线的交点为坐标(,)，同时，、分别为直角坐标系中直线的斜率和截距。由此得出，直角坐标系中的直线上的所有坐标点对应于霍夫变换空间中的一簇直线，同时，这些直线均相交于一个坐标点。反之，霍夫变换空间的一个坐标点对应于直角坐标系中的一条直线。

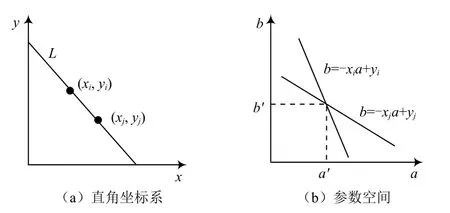
图1 直角坐标与参数空间的对应关系

通过将直角坐标系转换为霍夫变换空间的方式，能够轻松计算出直线的倾斜角度。但利用这种方法检测直线时会遇到一种特殊情况，即当直线为90°时，其直线对应的斜率为无穷大，此时该方法不能对直线进行处理。

为避免这种特殊情况，将检测方法转换为极坐标的形式进行计算，从而避免斜率无穷大的直线。极坐标表达式如公式（3）所示：

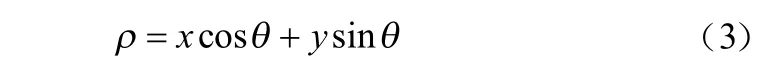
式中，角为轴与原点到直线距离线段的夹角；为直线到原点的垂直距离。直角坐标系与极坐标系关系如图2所示。

图2 直角坐标系与极坐标系关系

其基本原理与参数空间类似，将直角坐标系中的一个坐标点映射为极坐标中的一条曲线。直角坐标系中的一条直线映射为极坐标系中的一簇曲线，并且这些曲线相交于一点(,)。该极坐标点中的参数就是所求直角拟合后的斜率相关参数。从而将计算标记图像的倾斜角度转换为寻找霍夫变换空间中的极大值点，这样就将图像处理问题转变为了数学问题。

具体的直线拟合算法如下：

假设一幅标记图像为，其尺寸为×。图像中任一点(x,y)处的像素值为(x,y)。在霍夫变换空间中将平均赋值为个离散值，且满足∈[0, π)，为采样的个数。定义参数空间直线拟合公式如式（4）所示：

式中，=0, 1, ...,-1，=0, 1, ...,-1。

在显著特征的标记图像中，采用霍夫变换参数空间直线拟合的方法：

（1）对(,)参数空间做离散化处理，并定义对应的累加器，初始化为0。

（2）对标记图像进行搜索，并定义每一个坐标点(x,y)处的极坐标方程=xcos+ysin。

（3）在霍夫变换参数空间中计算所对应的，确定(,)。

（4）搜索整幅标记图像，将获取的值(,)对应的累加器加1。

计算完毕后，找到最大的值，并标记对应的(,)。此时，参数(,)即为直线拟合对应的相关参数。

显著特征标记图像采用霍夫变换直线拟合的参数空间示意图，如图3所示。标记图像在参数空间中形成了很多白色点，这就将直线拟合问题转变为了寻找参数空间中最亮的白色点。该点对应的即为所求直线拟合的参数。霍夫变换对直线拟合的条件要求较低，其有较好的抗噪声能力，且其检测精度较高，计算速度快。

图3 霍夫变换示意图

1.2 标记图像倾斜校正

通过直线拟合获取标记图像倾斜角度后，要对标记图像进行倾斜校正。在倾斜校正过程中对图像的细节特征会造成损失，因此会影响检测精度。所以对标记图像倾斜校正的研究具有重要意义。

图像校正的算法如下：假设一幅标记图像为，其中的一个像素点为(,)。将该像素点顺时针旋转角度，则旋转后的像素点坐标位置为(,)。图像旋转示意图如图4所示。

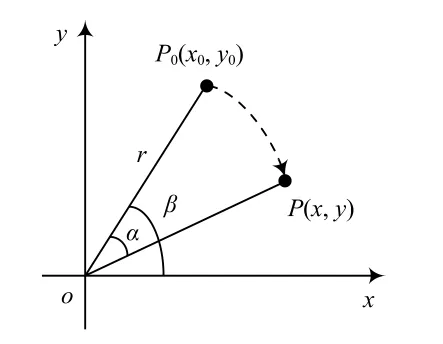
图4 图像旋转示意图

图4中，为像素点到坐标原点的距离，为像素点到坐标原点的直线与轴夹角，则像素点可用公式（5）表示：

旋转角度后的像素点可表示为公式（6）所示：

将公式（6）转换为矩阵形式，如式（7）所示：

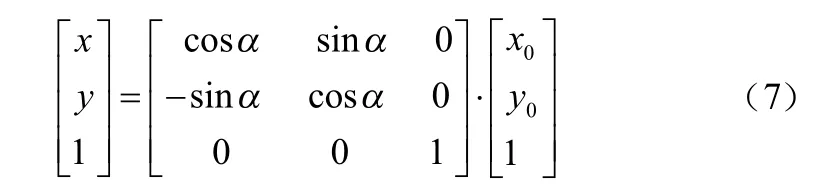
逆变换为式（8）所示：

在图像旋转过程中，如果采用公式（7）计算，则可能会出现标记图像旋转后无对应像素点的现象。因为像素点坐标均为整数，所以将坐标旋转公式进行逆变换。即采用反向映射方法，将旋转后的像素点按照映射关系确定原像素点。公式（8）即为旋转坐标公式。

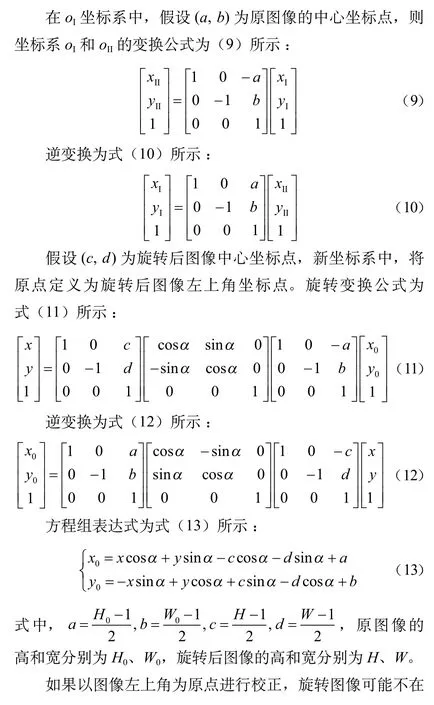
在实际工程问题中，一般都是以图像中心为原点进行校正。因此在对图像校正之前，要进行坐标变换。坐标系变换如图5所示。

图5 坐标系转换示意图

2 图像插值

利用坐标校正公式（13）进行计算时，主要针对的数据类型为浮点型。因为校正后的像素坐标可能是非整数，即校正后图像像素找不到对应的原图像像素。所以要将非整数像素坐标变为整数像素坐标，即图像插值。图像插值的计算速度和精度是矛盾的，因此需要根据实际工程来确定插值算法。计算速度和精度取折中的最优算法是双线性插值方法。

双线性插值算法的原理：设校正后某一个像素点在原图的映射坐标为 (,)，灰度值为(,)。(,)，(+1,)，(+1,+1)，(,+1)分别为(,)4个相邻点，且≤≤+1，≤≤+1。对应的灰度值为(,)，(,+1)，(+1,+1)，(,+1)。

（1）由(,)和(+1,)的灰度值求出(,)的值，如式（15）所示：

（2） 再由(,+1)和(+1,+1)求出(,+1)的值。如式（16）所示：

（3） 最后由(,)和(,+1)的值求出(,)。即式（17）所示：

在插值算法过程中，定义[]为不超过的最大整数值。式（17）中，=[]，=[]，=-[]，=-[]。双线性插值法如图6所示。

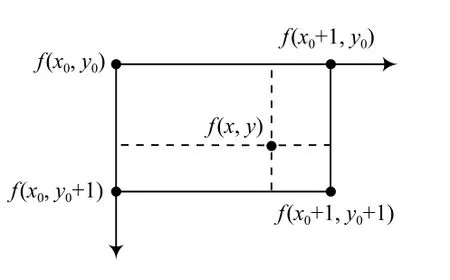
图6 双线性插值法

标记图像校正如图7所示。

图7 标记图像校正效果图

3 结 语

本文对显著特征的标记图像倾斜校正算法进行了研究。通过分析实际工程中对计算速度和检测精度的要求，提出一种更优的校正算法。该算法不仅具有较高的计算速度，同时也保护了标记图像的边缘特征点，从而提高了检测精度。最终破解了计算速度和检测精度间的矛盾。该图像校正方法适用于对图像处理速度和检测精度均有较高要求的场合。