基于CNN-LSTM-PSO的私有云故障检测

曹炳尧，柏 杰，侯佩儒

(上海大学 特种光纤与光接入网重点实验室，上海 200444)

0 引言

私有云的高可靠性是保障业务系统及云上作业正常运行的关键因素，在基于私有云环境本身高可靠的基础上实现对私有云的故障检测可以及时排除故障因素，进一步增强系统可靠性。目前在故障检测方面大多直接对系统级别故障数据进行检测，该方式在故障种类单一时可获得较好的预测结果[1]，但在私有云这类多因素故障的场景中效果并不理想。同时在正常私有云环境下，单靠运维人员对监控指标、运行日志等海量数据进行分析，排查潜在风险，也存在数据处理困难，排查准确率低，流程效率缓慢等缺点。

因此，针对上述问题，本文根据私有云监控指标的时间序列数据，采用X11分解算法对监控指标数据进行预处理获取特征数据并作为神经网络输入，将卷积神经网络(CNN)和长短期记忆(LSTM)循环神经网络融合进行模型构建，实现对监控指标时间序列的训练和预测。由于LSTM网络克服了RNN对时间序列预测时存在的梯度爆炸和梯度消失等问题，目前LSTM模型在时间序列上得到了广泛应用，并且在私有云监控指标的预测中表现也比较突出。

文献[2]验证了LSTM模型在云环境下对监控指标时间序列比单一模型在预测上具备精度更高的优势。Sudhakar[3]结合RNN和LSTM模型对服务器工作负载进行预测，并通过对比验证了预测效果其优于ARIMA模型，但相较而言其预测时间更长。Zhang等人[4]将萤火虫智能优化算法对LSTM预测模型进行优化实现对云主机负载的预测，提高了峰谷值处的预测精度。文献[5]提出了GRU-LSTM组合模型对云计算资源负载进行预测，提高了预测精度的同时减少了预测时间。文献[6]进一步对LSTM模型进行优化，结合PF模型提高了突发负载时预测精度。文献[7]结合果蝇优化算法对LSTM模型进行改进，通过对果蝇算法的寻优能力的提高加强了预测的精确度，但是存在突发状况变化的预测精度低的缺点。

上文实验中，通过将LSTM模型和其他算法结合的方式实现时间序列预测，这种多模型体系往往在预测精度上高于单一模型，但是一方面部分模型在LSTM超参数的选择往往采用试错法或者只进行简单的优化，而忽略超参数对模型预测效果的影响，另一方面在简单优化超参数的模型中往往仅采用单一LSTM网络结构进行预测，预测精度又没有复合模型高。本文在将LSTM神经网络模型和CNN神经网络结合的基础上，利用PSO算法实现超参数的优化工作，并采用采用高斯正态分布实现确定预测的波动范围，设定其上下限阈值，从而对真实数据进行故障检测，使其在预测结果及故障检测中产生更好的效果。最后通过和单一模型以及多模型结合的预测方法进行多方面对比，从而展示、分析本文设计算法的优缺性。

1 相关理论与技术

本节主要介绍卷积神经网络(CNN)、循环神经网络(RNN)、长短期记忆神经网络(LSTM)以及粒子群优化算法(PSO)。神经网络是一门重要的机器学习技术，它通过模拟人脑的神经网络以期实现近似人脑功能的人工智能技术，而粒子群优化算法是群集智能的一种，为多主体优化系统体系中的一种算法。

1.1 卷积神经网络

卷积神经网络(CNN，convolutional neural network)是一种可以同时学习多种特征的深度神经网络，目前在已被广泛应用于多个领域，包括图像、语言识别，资源预测等[8]。CNN的网络结构由输入层、卷积层、池化层、全连接层以及输出层构成，其中卷积层和池化层通过相互配合可以学习并总结历史数据的抽象特征信息，其中卷积层对输入数据进行滤波工作，计算提取出数据的建模特征，具体计算方式如公式(1)，从而挖掘出数据特征向量关联关系，池化层会在获取的特征信息基础上保留卷积后的主要特征的同时降低网络复杂度，提升模型特征信息提取效果。基于CNN算法的优越性已经有很多研究人员将CNN成功应用于故障诊断中[9]。

(1)

式中，⊗表示卷积计算；F表示卷积层输入数据；ω表示卷积核的权重参数；C、Wf、Hf分别为卷积核的通道数、宽度以及高度。

一般情况下一维CNN网络处理时间序列数据具有更佳效果，二维CNN网络则在图像处理方面效果更好，本文中数据为时间序列数据，选择一维CNN网络。在经过池化层后将数据输入全连接层，将多维数据转化为一维。一维CNN网络结构如图1所示。

图1 一维CNN结构图

此外，CNN网络的神经元之间共享一个卷积滤波器的参数，从而大幅度减少网络冗余参数，避免过拟合现象。

1.2 循环神经网络

传统的神经网络如CNN神经网络在同层之间神经元不会互相传递信息，输出信号仅与输入信号相关，因此无法处理具有连续关系的输入信号且无记忆能力，对本文中的时间序列数据处理效果不佳。为此要构建具备记忆功能的神经网络模型，可采用循环神经网络(RNN，recurrent neural network)，通过梯度下降算法、权重共享以及前向反馈机制实现对时间序列的预测，目前循环神经网络已被广泛应用在自然语言处理[10]、计算机视觉[11]、计算机生物学等领域，在计算机及IT系统领域中的应用还较少。

未展开的循环神经网络结构如图2(a)所示，其网络结构同传统神经网络相同，包含输入层、隐藏层和输出层。图中A表示神经网络模型，xt表示输入时间序列在t时刻的数据，ht表示在t时刻的输出数据，其中区别于CNN网络的是隐藏层输出的数据除了会将信息流输出到ht，同时会将当前时刻的神经元信息传递到下一时刻的神经元，并在下一时刻加以利用，U、W、V为神经网络中的权重矩阵。这种链式结构揭示了RNN本质上是与时间序列相关的，但是RNN虽然理论上可以保留所有的历史时刻的信息，在实际情况下，信息的传递会因为时间间隔造成衰减效应，即梯度消失，这种情况下会严重降低对数据有长期依赖的信息在处理上的效果。并且RNN模型由于在训练时需要预先确定延迟窗口长度，但是该值的改变难以确定，其最优值也难以获取。所以本文将进一步研究其优化算法LSTM。

图2 RNN和LSTM结构图

1.3 LSTM神经网络原理

由于RNN上述的问题，文献[12]提到了长短期记忆神经网络(LSTM，long short-term memory)。LSTM通过实现时间递归，将隐藏层中RNN细胞替换为LSTM细胞，并在细胞内采用“门”的概念实现长距离的保留长期历史信息[13]。图2(b)为LSTM神经网络结构图。和RNN网络相比，此处LSTM网络添加了表示细胞状态，用以表示当前LSTM网络的状态信息并用来传递到下一时刻的LSTM网络中，其次在隐藏层中设计了3个门结构：ft遗忘门、it记忆门和ot输出门，LSTM神经元隐藏层网络结构如图3所示。

图3 LSTM神经元隐藏层网络结构

遗忘门决定了上一周期的时间序列是否从历史数据中进行过滤，记忆门与之相反，它决定输入信息Xt和Ht-1中需要保留的信息，主要将该循环周期内的需要存储的时间序列信息存储到神经元状态中，Ct细胞状态通过更新传递到下一时刻Ct-1，输出门并非最终输出状态，仅为当前时刻输出信号，需要作为下一时刻输入信号传递到下一阶段，详细计算方式如公式(2)～(6)：

ft=σ(Wf·[ht-1,xt]+bf)

(2)

it=σ(Wi·[ht-1,xt]+bi)

(3)

c′=tanh(Wc·[ht-1,xt]+bc)

(4)

ot=σ(Wo·[ht-1,xt]+bo)

(5)

ht=ot·tanh(c)

(6)

式中，W是门的权重矩阵，σ表示sigmod函数，b是门的偏置项。

由获取到的时间序列数据输入当前时刻数据Xt，前一时刻的细胞状态Ct+1作为该网络神经元状态输入，将当前时刻的信息Xt通过遗忘门ft处理，去除冗余信息以后和输入门合并生成当前时刻的细胞状态Ct，同时由处理过的历史信息与经过记忆门it处理后的输入信息进行运算得到当前时刻输出信号ht，该信号也将传递到下一时神经元。

LSTM神经网络通过增加细胞状态，并经过遗忘门和记忆门更新细胞状态，从而长时间保存了时间序列数据的历史信息，有效缓解了梯度消失、梯度爆炸以及长期依赖的问题。

1.4 粒子群优化算法

在LSTM算法中，除了LSTM内部网络结构的参数需要通过训练得到，还存在大量需要在训练网络模型之前预设的参数，这些参数被称为超参数(hyper-parameters)，这些参数在训练过程中保存不变，但其值对模型训练具有较大影响，训练完成后通常需要进行调优，找到一组全局最优超参数。目前超参数优化算法包括网格搜索法、随即搜索算法、贝叶斯算法等，本文采用粒子群优化算法(PSO，particle swarm optimization)对LSTM模型的超参数进行优化。

PSO算法是由Eberhart和Kennedy提出，通过模仿大自然群居动物的集群觅食行为，通过在群体中的个体间的互相关系来寻找最优解[14]。其凭借易于实现、参数少等优点被广泛应用于神经网络训练、遗传算法等领域。粒子群通过粒子间信息交换保留记忆进行迭代向全局最优解进行演变，获取最优粒子实现寻优。

寻优超参数被包含着粒子群的向量内，设置M个参数构成搜索空间创建粒子群，粒子群内包含N个粒子，计算具体方式如公式(7)：

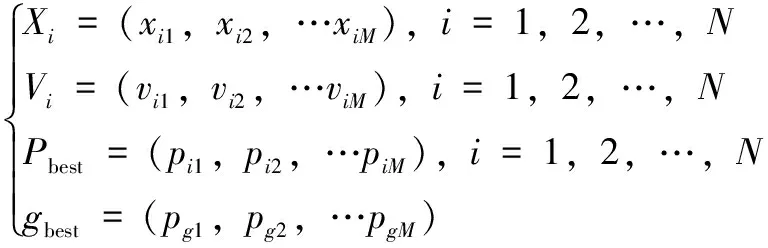
(7)

式中，Xi表示粒子的位置，Vi表示粒子的寻优速度，Pbest表示第i个粒子的搜索到的最优位置，gbest表示迭代后整个粒子群搜索到的最优位置。

本文将PSO应用于LSTM的超参数优化中，并建立LSTM-PSO模型，以寻找超参数的全局最优解。

2 方案设计

根据私有云监控指标时间序列数据的特点，结合第1节相关理论，本节提出CNN-LSTM-PSO模型的故障检测的方案，首先采用X11分解法等技术对时间序列进行数据预处理，并在此基础上选择为LSTM模型添加卷积层的方案实现对模型的训练及预测，最后基于多层PSO算法完成对超参的选优算法以进一步优化预测效果，并使用高斯正态分布进行阈值选定。

2.1 整体方案设计

本文以LSTM神经网络为核心，将实现过程分为七层，包括数据预处理层、卷积层、输入层、隐藏层、网络训练场、超参优化层和输出层，其基本实现框图如图4所示。实现过程描述如下：

步骤1：数据预处理层将短采样周期监控指标时间序列进行平滑处理，并将数据分解得到周期和趋势数据。

步骤2：卷积层将数据归一化，并使用CNN网络模型进行特征学习并提取。

步骤3：输入层对特征数据进行训练集划分，数据分割以满足LSTM神经网络输入要求。

步骤4：隐藏层为LSTM核心层，构成网络训练模型核心，实现网络训练及结果预测。

步骤5：网络训练层通过对训练过程中的模型输出和实际数据计算损失模型loss，并采用adam优化网络算法优化权重矩阵，完成模型参数的训练。

步骤6：超参优化层初始化粒子群，并使用PSO优化算法迭代训练获取全局最优超参数。

步骤7：输出层通过训练完成的神经网络对测试数据集进行预测，同时通过高斯正态分布计算预测值的阈值，通过比较真实数据是否在该范围内以检测该时刻监控指标数据是否存在异常。

图4 整体方案设计

2.2 基于X11分解法的时间序列预处理

本文监控私有云监控指标其周期粒度一般为30 s或者1 min，考虑到短周期时间序列的波动性大，易造成毛刺等现在，同时为了统一周期粒度指标，对数据先进行平滑处理，将周期重置为3 min，单周期值取该周期范围内子周期的平均值。同时时间序列通常可以被分解为趋势、周期及残差3个变量，如经典分解法可将时间序列分解为周期成分、趋势成分和残差，其计算方式如公式(8):

y(t)=S(t)+T(t)+R(t)

(8)

式中，S(t)为周期成分(seasonal component)，T(t)为趋势成分(trend-cycle component),R(t)为残差成分(remainder component)。

但在本文中的监控指标的时间序列除了会被上述因素影响之外，还会受到季节、月度变化等因素的影响，为此本文采用X11算法以去除月份和季节因素，在获得的趋势周期成分中，在使用经典分解法即公式(8)进而获取到精确的周期数据和趋势数据，其中X11算法基本公式如式(9)：

Yt=CtStItPtDt

(9)

式中，Yt是原始序列，Ct是趋势周期成分，St是季节成分，It是先验月因子，Pt是工作日因子，Dt是不规则成分。

通过结合X11分解法和经典分解法获取到精确的周期和趋势数据。X11分解法(X11 decomposition)可以获得完整数据的所有趋势成分，对于假期、季节等已知的影响因素都有着更好的处理结果。

2.3 基于CNN-LSTM网络模型训练及预测

传统的LSTM模型虽然可以对中长时间序列进行预测，但是由于其遗忘门的存在，在对大规模数据进行训练时，会遗忘部分重要信息，造成模型训练效果出现退化现象。而卷积神经网络CNN通过其卷积层可以挖掘历史数据中更深层次的特征信息。因此通过CNN网络先进行特征信息学习后再传入LSTM网络进行时间序列学习将使模型对未来时间数据的数据更精准。

网络训练和预测的核心是隐藏层，通过训练获取隐藏层矩阵参数，并以该模型对数据进行预测。经过2.2小结预处理后得到处理后的周期和趋势时间序列分别为S(t)和T(t)。此处以周期序列S(t)为例，设S(t)={s1,s2,…,sn}，在卷积层采用z-score对特征值的训练集进行归一化处理，将其映射为均值为0，方差为1的标准序列，以此消除特征单位及尺度等影响，其计算方式如公式(10),完成归一化的数据表示为

(10)

式中，x为实际值，μ为均值，σ为标准差，z为归一化结果。

初始训练模型采用64单元的LSTM层，时间步长为12，预测长度为10。同时为防止过拟合的发生，采用EarlyStop和Dropout技术，其中早停法(EarlyStop)通过在模型验证集上表现开始下降时停止训练避免过拟合，随机丢弃层(Dropout)通过一定概率的让部分神经元不参加模型训练以减少过拟合现象。损失模型(loss)采用均方误差(MSE，mean-square error)进行计算，并以该损失函数最小为目标，给定初始的超参数，并使用Adam优化算法对隐藏层的网络权重进行更新，进而获得训练模型并对测试集进行预测。

2.4 基于PSO算法的超参数优选

LSTM常见超参数包括学习率η、迭代训练次数C、分割窗口长度L、神经元个数N、状态向量大小Sstate等。其中学习率η绝对目标函数的收敛能力，合适的学习率可以其在合适时间内收敛到局部最小值，反之学习率过大可能会造成模型震荡导致无法收敛，过小则学习效果欠佳，易造成模型训练用时增加，本文学习率的设置范围为[0.01,0.001]。训练次数C表示本文需要进行图3中网络训练层Adam优化网络权重参数的次数，训练次数过小无法得到最优网络权重参数，过多会增加训练时长，浪费计算机计算资源，对实时检测的时效性有一定影响[15]。

本文将基于PSO对4个关键超参数(学习率η、迭代训练次数C、分割窗口长度L、神经元个数N)进行选优，将这4个超参数作为PSO粒子，通过更新粒子的速度和位置获取每个粒子全局最优值，LSTM-PSO模型流程如图5所示。

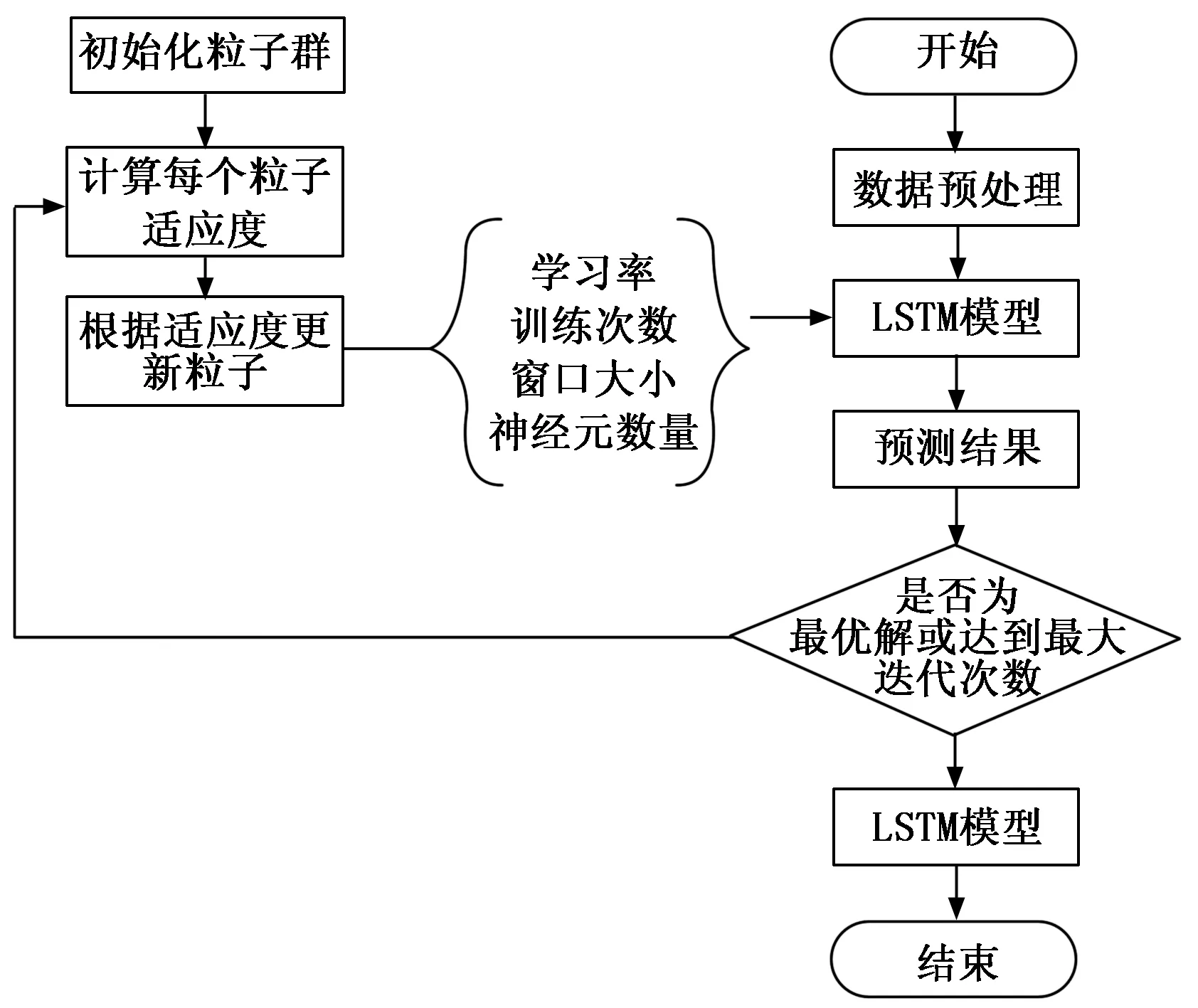
图5 LSTM-PSO预测模型流程图

在图4的基础上，将LSTM模型训练过程置于PSO模型内，对于关键的超参数先设置经验值进行模型训练，然后根据表1中超参数取值范围通过计算粒子适应度更新粒子迭代训练获取最优解。如表1为本文设置超参数取值范围。

表1 超参数取值范围

PSO通过适应度来评价解的好坏，本文中适应度函数通过设置真实值和预测值的平均百分比误差(MAPE，mean absolute percentage error)的最小值来实现，公式如(11)和(12):

(11)

F(x)=min(M)

(12)

式(11)中,n表示预测时间序列的监控项个数，Pact表示监控项的真实值，Ppre表示监控预测值，M表示MAPE，式(12)中F表示适应度。

2.5 基于高斯正态分布的阈值选定

高斯正态分布模型计算简单，且运算速度快，在进行故障实时检测中更快速、准确。通过对样本值的均差和方差来计算整体概率分布，设随机变量服从一个位置参数、尺度参数为的概率分布，且其概率密度函数为式(13)，则该随机变量为正态随机变量，且符合正态分布[16]。

(13)

本文进行预测的趋势周期模型符合正态分布。正态分布进行阈值计算求得阈值上限和阈值下限，在本文中必须当趋势周期实际值超过阈值时，将其判定为出现故障。异常检测的实际原理就是小概率事件一般不会发生，当出现时即视为出现故障[17]。

3 实验测试与分析

3.1 数据集及故障类型

在私有云环境中，按照固定时间采集到监控项指标数据作为时间序列，其中监控项指标包括CPU、内存等基本监控指标、电源开断、物理服务器风扇转速等物理指标以及应用服务状态、端口状态等监控指标。本文主要以已搭建私有云内某虚拟主机CPU、内存、磁盘3种监控指标作为时间序列进行数据分析和模型对比，每条指标选取1年的数据，初始周期统一取3 min，将前3个月数据作为训练集，后9个月数据作为测试集。

而在上述指标中呈现的故障类型也存在不同的形式，通常包括点异常、集合异常以及峰值异常，如图6所示。其中点异常可以在检测期间单独处理而无需考虑时间关系，所以最好处理，通常简单阈值设定的方法即可处理。峰值异常则取决于其相邻数据点的值，因此需要检测局部信息，而集合异常是由于一系列数据点同时表现出异常而产生的，所以需要对时间序列进行处理，本文采用的CNN-LSTM-PSO模型对此有着很好的检测效果。

图6 私有云监控指标故障类型

同时为对模型预测结果进行比较，本文采用标准差(SD, standarddeviation)来反映实际值与预测值的离散程度[18]，模型监控指标的预测值和实际值分别进行均方根误差(RMSE，rootmeansquareerror)、平均绝对误差(MAE，mean absolute error)和平均百分比误差(MAPE)的计算对预测结果的精确度进行比较，这3个值越低，表示误差越小，精度越高。其中RMSE、MAE计算方式如公式(14)、(15)，MAPE如公式(11)：

(14)

(15)

式中，yact表示第i个样点监控项的实际值，ypre表示第i个样点监控项的预测值。

故障检测的能力则使用精度(precision)、召回率(recall)和F1分数来评估，精度越高表示检测准确率越高，召回率越高表示漏检故障可能性越低，F1越高表示整体效果越好，计算方式如公式(16)～(18)所示：

(16)

(17)

(18)

式中，TP(truepositive)表示正确检测出的异常数，FP(false positive)表示正常数据被检测为故障的数量，FN(false negative)表示异常数据被检测为正常的数量。

3.2 对比模型

本文将会从以下几个时间序列模型和所提出的CNN-LSTM-PSO模型进行实验对比。

1)自回归移动平均(ARIMA，autoregressive integrated moving average model)模型基于时间序列的趋势变化、周期性和随机干扰实现对平稳时间序列的预测[19]。模型表示为ARIMA(p,d,q,其中p为自回归项数，d为差分项数，q为移动平均项数[20]。本文基于ARIMA模型，并结合网格搜索法对ARIMA模型的3个参数进行调优，从而实现对监控指标的时间序列预测。

2)Holt-Winters指数平滑不同于常见的时间序列分解法，其基本思想是通过加权平均移动法来实现时间序列预测[21]。Holt-Winters可以在捕捉周期分量和趋势分量的同时直接进一步捕捉到季节分量，以表示序列数据的局部特征变化，其原理是通过将时间序列上远近时刻的数据进行权重划分，其中较近时刻给予较大权值，较远时刻给予较小的权值从而同时兼顾所有时刻，实现时间序列的预测[22]。

3)将本文第一节提到的RNN模型以及单独使用LSTM模型的预测进行效果比对。

4)采用论文[5]的模型，将GRU和LSTM组合构建GRU-LSTM模型进行模型训练和预测。该模型先使用GRU网络提取监控指标的输入变量特征，构成高维映射空间时序性特征向量，然后将结果输入到LSTM网络进行训练。

3.3 平台环境

本文使用计算机配置如下：处理器为Intel(R) Core(TM) i7-8750H，CPU频率为2.2 GHz和2.21 Hz；内存为32 GB；操作系统为Windows11(64位)；程序设计语言位Python3.7，采用pandas、keras、states等程序包。

3.4 实验结果

为直观体现本文模型的预测效果，以监控指标CPU使用率作为预测数据，选取数据的间隔时间作为横坐标，CPU使用率作为纵坐标。图7、图8分别为本文设计模型CNN-LSTM-PSO和GRU-LSTM模型对CPU指标进行预测的结果，可以看到两种模型都可以大致预测到数据的走向，但本文预测拟合效果更好，精度更高，而GRU-LSTM在线性上升或者下降部分效果较好，但在谷峰值位置处明显有部分数据预测效果不佳，不如本文模型。由此可看到CNN结合LSTM的模型对极端峰、谷值都有着更好的拟合效果。且在抖动频繁的时间点，CNN-LSTM-PSO模型的预测结果更接近真实值，这也证明了通过PSO实现超参选择在一定程度上提高了模型的精确度。

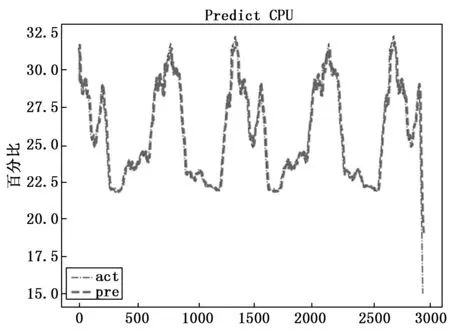
图7 CNN-LSTM-PSO模型预测效果

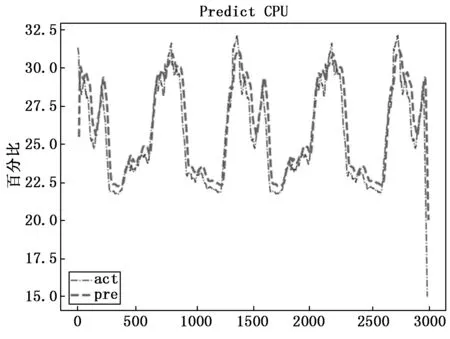
图8 GRU-LSTM模型预测效果

为进一步说明CNN-LSTM-PSO模型预测性能，将其分别与ARIMA、Holt-Winters、RNN、LSTM以及GRU-LSTM五种模型进行对比，并以RMSE、MAE以及MAPE作为参考指标，同时计算模型训练和预测的耗时，结果如表2所示。

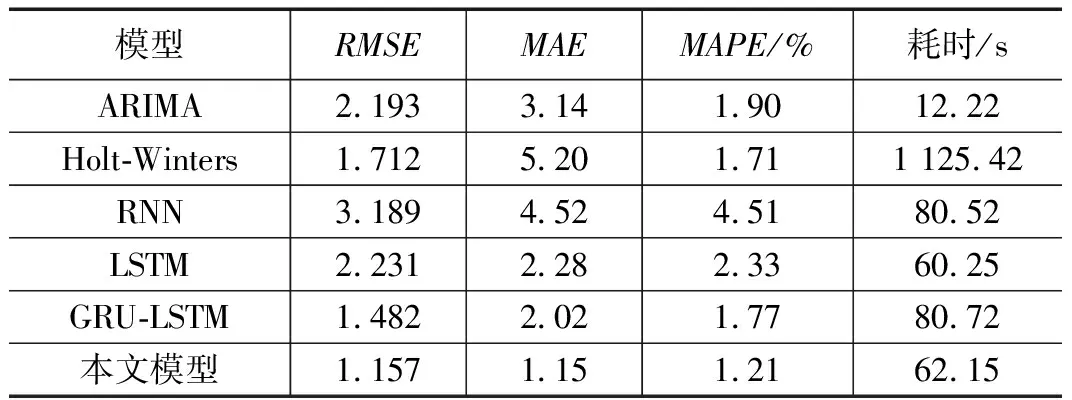
表2 ARIMA、Holt-Winters、RNN、LSTM、GRU-LSTM及本文模型预测效果对比结果

从表2可以看出，RNN和LSTM神经网络模型误差都比较大，预测准确度最不理想，Holt-Winters预测效果略有提升，但是其耗时过长，ARIMA模型耗时最短，但是其预测效果较差，论文[5]中所提的GRU-LSTM模型在可控耗时情况下其预测效果也较好，但是相比于本文的CNN-LSTM-PSO模型在预测效果上还有一定差距，其中对于监控指标波动处的预测效果差距更大。并且本文模型在训练和预测的总耗时上虽比ARIMA和LSTM模型略高，但相比于Holt-Winter、RNN和GRU-LSTM都要略快一些。可以看出，本文提出的CNN-LSTM-PSO在模型性能上有着较好的优化。最后本文通过高斯正态分布进行阈值选定。当实际值超过图中阴影部分上下阈值时，即判定此时出现故障。

本文通过精度、召回率和F1值来比较本文设计模型的故障检测效果，如表3为内存使用率的性能比较结果。由上文预测效果可以分析出单RNN模型和LSTM模型效果较差，此处将不在进行比较。

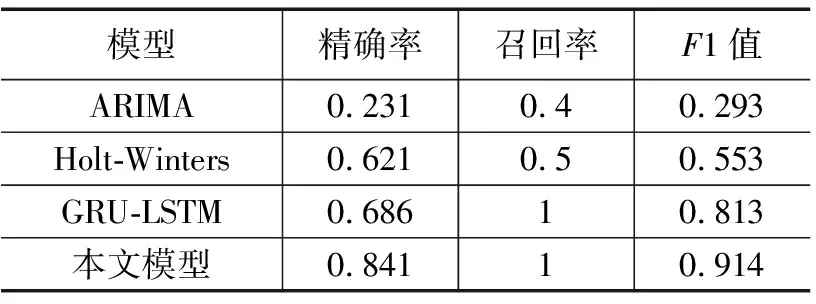
表3 ARIMA、Holt-Winters、GRU-LSTM及本文模型故障检测效果对比结果

结果表明，相对于本文提出的模型，ARIMA、Holt-Winters模型的精度、召回率和F1值都有所欠缺，整体效果较差。而GRU-LSTM模型和本文模型召唤率都较好，但是本文模型精确率更优，因此F1值也最好。可以看出，本文提出的CNN-LSTM-PSO模型在故障检测效果上有着明显的优势。

3.5 参数选优

在进行超参选优时，LSTM网络的超参数范围根据表格1中的范围进行设置，同时设置种子群规模seed为30，最大迭代次数40。寻优主要通过2.4节中提高的LSTM预测模型的参数得结果，包括适应度F(x)和超参数学习率η、迭代训练次数C、分割窗口长度L、神经元个数N的变化趋势，详细结果如如图9所示。

图9 PSO优化结果曲线图

通过PSO对LSTM网络的超参数进行选优，当迭代次数达到19时适应度最优，且迭代次数最少，如图9(a)所示，此时3个超参数都达到最优效果。此时通过图9(b)、9(c)、9(d)可以看出学习效率为0.007 6，分割窗口长度为652，神经元个数为369。通过对超参数变化曲线图分析可以发现超参数都有两个峰值，在迭代次数为19和迭代次数为27分别有一个高峰值，但是迭代次数在19时效果更好。

4 结束语

针对私有云故障检测的问题，本文提出了CNN-LSTM-PSO模型对关键监控指标故障的检测方法，采用X11分解法和经典分解算法可以获取时间序列的周期成分和趋势成分，同时使用CNN-LSTM模型可以对长时间序列预测有更好的拟合效果,利用PSO对LSTM模型网络的超参数进行选优工作，在避免简单人为确定超参数导致无法取得全局最优的同时，将超参选优的时间控制在确定时间内，保障模型预测的实时性。采用高斯正态分布确定阈值大小，最终实现了私有云的故障检测工作。

测试结果表明，相比较其他时间训练模型，本文提出的CNN-LSTM-PSO模型能够有效提高预测的精确度和准确性，同时训练及预测耗时在可控范围之内，在对私有云的故障检测中有着较好效果。