基于改进萤火虫算法优化的电力光纤线路状态预测模型研究

2022-08-26孔历波毛一凡欧阳李亮

计算机测量与控制 2022年8期

孔历波，毛一凡，欧阳李亮，康恺，何超

(浙江大有实业有限公司杭州科技发展分公司，杭州 310052)

0 引言

近年来，光纤通信由于损耗小、速度快、容量大合抗干扰等特性，在电力领域得到广泛的应用[1]。当光纤线路发生故障时，将导致电力通信中断，进而给用户及企业造成不可逆的损失。因光功率数据能够在全面表征电力光纤通信线路受各种参数的影响程度，故通过预测电力光纤光功率的发展趋势，能够达到预测通信线路未来状态的目的[2-4]。目前光纤维护主要通过在线实时获取光功率数据来进行，当光功率数据超越前期设定的阀值时，系统将开启光时域反射仪(OTDR，optical time domain reflectometer)进行测试，通过分析测试得到的曲线进行光纤故障诊断与定位，之后由现场工作人员进行维修，从而恢复电力通信。但上述方法仅能实时掌握电力通信线路的实时状态，处理已经发生的故障，不能预测和提前分析线路状态未来的发展趋势，对未来故障进行有效的规避，因此基于电力光纤的光功率数据的特性，构建精准的光功率预测模型，提前掌握电力光纤线路状态成为下一阶段研究的重点[5-9]。

光功率是一种具备复杂性、时变性及非线性等特性的时间序列数据。近些年，国内外学者针对时间数据序列预测进行了大量的研究，并得到多种时间序列预测方法[10-16]，例如支持向量机 (SVM，support vector machine)模型、神经网络预测模型、自回归滑动平均(ARMA，auto-regressive and moving-average)模型、灰色预测模型等方法。SVM预测模型中核函数的类型及参数对其泛化性能和学习能力起到决定性作用，故选用单一核函数的SVM预测模型，呈现出较低的预测精度；神经网络预测模型处理非线性数据时，存在局部极小值和学习速度慢等问题；ARMA预测模型在对非线性时间序列数据进行处理时，首先需要进行平稳化处理，并且整体的预测精度相对较低。

针对上述的不足，学者们对预测算法进行改进和融合。文献[17]提出一种差分自回归移动平均模型与支持向量回归模型融合的功率预测模型(ARIMA-SVR，autoregressive integrated moving average model-support vector regression)光伏短期功率预测模型，实现短期光伏功率预测，提升电力系统光伏消纳和能源协调的整体能力；文献[18]提出一种自适应粒子群优化ARIMA-SVM光功率预测模型，对SVM的核参数进行优化，实现光功率数据未来趋势的预测；文献[19]提出一种ARIMA-RVM光功率预测模型，对光纤光功率数据进行预测；文献[20]提出一种长短记忆网络(LSTM，long short term memory network)光纤参数预测方法，实现光纤数据的短期预测；文献[21]提出自用自适应粒子群优化的ARIMA-GRU组合光功率趋势预测模型，实现了光功率预测，为电力光纤故障预警监测提供理论依据。

综上所述，在各行各业均有时间序列预测方法的成功案例，但在光纤光功率预测方面的研究和应用还处于探索阶段，预测的精度有待进一步的提升。本文基于光纤光功率预测的实际需求和前人研究成果，提出一种基于改进萤火虫算法优化的光功率预测模型(FA-ARIMA-GRU, firefly algorithm-autoregressive integrated moving average mode-gated recurrent unit)，实现光功率趋势的准确预测，进而提前掌握电力光纤的线路状态，实现预知光纤线路故障、有效规避故障和保障电力通信传输通畅不间断。

1 ARIMA-GRU 模型原理

光功率是一种具备复杂性、时变性及非线性等特性额定时间序列数据，故选用ARIMA模型对高频光功率数据进行预测；选用GRU模型对低频光功率数据进行预测，形成ARIMA-GRU组合光功率趋势预测模型，选用改进萤火虫算法对组合预测模型的参数进行优化，在一定程度提升光功率预测的精度，减小预测误差。光功率预测模型的过程如图1所示。

图1 电力光纤光功率预测流程图

1.1 数据预处理

1.1.1 数据分解

本文选用采用小波变换Mallat算法来对原始光功率数据进行分解，从而得到高频数据和低频数据，分解得到的数据长度为原来数据长度的一半。分解表达式为：

Xj+1=GXj,Zj+1=HZj,j=0,1,...,J

(1)

式中,H表示低通滤波器；G表示高通滤波器；j表示小波分解的层数；Zj+1表示在分辨率2-(j+1)下原始数据分解得到的高频分量数据；Xj+1表示在分辨率2-(j+1)下原始数据分解得到的低频分量数据。

1.1.2 数据重构

数据分解得到的高、低频数据利用Mallat算法进行重构，最终得到重构数据，重构数据的长度与原始数据一致。重构表达式为：

xj=H*xj+1+G*zj+1,j=0,1,...,J

(2)

式中，H*表示H的对偶算子；G*表示G的对偶算子。

1.2 ARIMA模型

ARIMA模型主要由自回归移动平均模块(ARMA，autoregressive moving average)、自回归模块(AR，autoregressive)和移动平均模块(MA，moving average)3个模块组成。

自回归模块主要采用变量的历史数据预测当前数据，其表达式为：

(3)

式中，γi表示自相关系数；yt表示当前的信息；εt表示误差；μ表示常数项；p表示阶数。

移动平均模块主要对预测过程当中所出现的随机波动情况进行解决，其表达式为：

(4)

式中，θi表示相关系数。

由自回归移动平均模块是上述两模块的结合，其表达式为：

(5)

将上述3个模型与差分法结合在一起便构成差分整合移动平均自回归模型，其通过模型解析和定阶(确定p、d和q的值，其中d取1或2)、参数估计和确定、模型验证3个阶段来进行构建。

1.3 GRU模型

GRU神经网络和LSTM神经网络具十分相似的网络结构，具体网络结构如图2所示。由图2可知，GRU神经网络主要包含重置门与更新门，其中更新门表示当前时间步长上接收上一步长状态信息的程度；重置门表示忽略上一步长信息的程度，两者均需要对当前时刻和前一步长时刻状态信息进行线性转换。

GRU模型构建步骤为：

1)更新信息确认。首先，当前输入状态xt和神经元上一时刻的输出ht-1相加；其次，将相加结果与更新门权重Wz相乘；最后运用sigmoid函数对乘积结果进行运算，具体的计算表达式为：

zt=σ(Wz·[ht-1,xt])

(6)

式中,σ表示sigmoid函数；Wz表示更新门权重；xt表示当前神经元的输入；zt表示更新门；

[]表示两向量相连接，即相加；ht表示本次神经元的输出，更新门输出值越大，则代表当前状态代入的上一神经元信息越多。

图2 GRU神经网络模型

rt=σ(Wr·[ht-1,xt])

(7)

(8)

(9)

yt=σ(Wo·ht)

(10)

式中,yt表示GRU神经元整体总输出；Wo表示输出门权重。

光纤光功率的高频数据选用ARIMA模型来进行预测，低频数据选用GRU模型进行预测，将高、低频预测结果相加得到ARIMA-GRU组合预测模型。

2 基于改进FA的ARIMA-GRU模型优化

由上节可知，ARIMA模型在构建过程中p、q的值仅是基于偏相关和自相关分析得到，GRU模型输入长度设定也是通过经验得到，故上述各个参数均有一定程度的优化空间，本节选用改进萤火虫算法对ARIMA-GRU预测模型进行优化，从而提升电力光纤光率预测的准确性，更加精准的掌握电力光纤线路状态。

2.1 改进萤火虫优化算法 (FA)

2.1.1 标准萤火虫优化算法

随着计算机技术的不断创新，智能技术的不断发展，更多新型的智能算法应运而生，为了对模型优化及参数选择等问题进行解决，Yang[22]于2008年提出一种针对模型优化及参数选择[25]的算法，即萤火虫算法，其(FA，firefly algorithm )是众多智能算法中的一种。该算法通过对自然界当中萤火虫群体行为进行模拟，进而达到对模型的优化求解的目的，具有操作简便、参数设置少及计算效率高等优点。在光线功率预测问题当中，预测模型的求解及优化过程就是萤火虫之间移动位置、彼此吸引及优胜劣汰的过程。在整个算法优化进程中，萤火虫彼此之间的吸引是由吸引度和亮度决定。亮度较高的萤火虫代表模型可行解处于优越的位置，并且此时的萤火虫具备较强的吸引力。最亮的萤火虫就是模型优化及参数选择的最优解。随着传播介质的吸收与空间距离的增加，萤火虫的亮度逐渐变暗，并且其位置在每次迭代计算过程中不断地更新，进而问题的解也得到进一步的优化。

对于FA基本原理的数学表达式为：

1)相对荧光亮度:

I(r)=I0e-γr2

(11)

式中，γ表示传播介质的光吸收系数；I0表示初始萤火虫亮度；r表示两萤火虫的笛卡尔距离，其表达式为：

(12)

式中，(xi-xj)、(yi-yj)分别表示第i、j只萤火虫在空间当中的位置。

2)吸引度:

β(r)=(β0-βmin)e-γr2

(12)

式中，β0表示r=0处，即光源处的吸引度大小；βmin表示最小吸引力值。

3)萤火虫位置移动:

(13)

式中,α表示扰动步长因子，通常其取值范围为[0,1]；rand()表示某个随机扰动，通常其为取值范围[-0.5,0.5]内均匀分布或U(0,1)标准正态分布；r表示第i个和第j个萤火虫的笛卡尔距离；[w,b]j表示亮度较第i萤火虫更亮的萤火虫的位置。

萤火虫算法整体流程如图3所示。

图3 萤火虫算法整体流程图

2.1.2 改进萤火虫优化算法

虽然标准萤火虫算法具备操作简便、参数设置少、计算效率高及寻优能力强等优点，但是其在解决非线性和高维度问题时，存在局部最优收敛与收敛速度慢等智能算法的通病。传统萤火虫算法步长因子选用固定值，设置过小会造成萤火虫移动缓慢，从而需要较长时间才能达到收敛，甚至无法达到收敛；设置过大会造成萤火虫反复振荡于最优解附近。

本文参考梯度优化算法当中的Adam算法[24]和 RMSprop算法[25]，对萤火虫算法进行改进，对整体距离进行指数加权平均，并设计了迭代衰减步长因子。改进萤火虫算法还对偏差修正进行考虑，在一定程度上改善初始误差大和过拟合等问题。

2.2 基于改进FA的ARIMA-GRU模型优化

本文采用的改进萤火虫算法当中，各个萤火虫的位置表示ARIMA-GRU组合模型参数的一个可行解；萤火虫位置的适应度用萤火虫的亮度表示。各个萤火虫均会朝着比自己亮度高的个体进行飞行，从而搜寻到更优的位置。各萤火虫吸引其它萤火虫的程度与两者距离成反比，与亮度成正比。改进萤火虫算法优化ARIMA-GRU模型的整体流程如图4所示。由图4可以看出，改进萤火虫算反对自然界中的萤火虫行为进行模拟，通过多次迭代搜索到群里中最亮萤火虫的位置，输出训练ARIMA-GRU模型的最优参数，形成FA-ARIMA-GRU复合模型。

基于改进萤火虫算法的ARIMA-GRU模型优化流程为：

1)初始化。萤火虫的数量假设为N，并对各个萤火虫的位置进行随机初始化。设置介质对光的初始吸引度β0=1.0；初始步长α=0.3；吸收系数γ=1，吸引度的表达式为：

β(r)=(βmax-βmin)e-γr2+βmin

(14)

式中,βmax=1,βmin=0.2，式(14)保证任意两萤火虫之间的吸引度保持在[0.2,1]区间内。

2)计算各个萤火虫适应度值。适应度选用R2指标，其表达式为：

(15)

图4 基于改进萤火虫算法的ARIMA-GRU模型优化流程

3)移动。各个萤火虫飞向比其亮度更大的萤火虫，飞行过程中萤火虫的位置变化可以通以下表达式进行表示：

(β0e-γr2([w,b]j+arand())2

(16)

(17)

式中,α表示扰动步长因子，通常其取值范围为[0,1]；rand()表示某个随机扰动，通常其为取值范围[-0.5,0.5]内均匀分布或U(0,1)标准正态分布；r表示第i个和第j个萤火虫的笛卡尔距离；[w,b]j表示亮度较第i萤火虫更亮的萤火虫的位置。为了进一步提升算法的收敛性，令步长呈现迭代衰减态势，那么第t步长的表达式为：

α=s1α+(1-s1)*(0.97)t

(18)

其中:s1表示一阶矩估计的指数衰减率，s1=0.9；s2表示二阶矩估计的指数衰减率，s2=0.999。

群体中亮度最大的萤火虫不会向另外萤火虫的位置进行移动，其位置更新基于以下表达式：

(19)

4)对移动至新位置的萤火虫的适应度值进行计算，如移动后的位置比原有位置优越，此时位置移动生效，反之萤火虫不发生移动，停留在原地。

5)为了防止优化后模型出现过拟合现象，该算法设定一个适应度阈值。当每次迭代完成后，对当前最优适应度值进行记录，如果最优适应值大于等于设定的适应度阈值或者该算法已经达到最大迭代次数，此时算法输出搜寻到的最优参数，反之跳转至步骤2)继续进行迭代。

6)采用改进萤火虫算法输出的最优参数来构建ARIMA-GRU模型。

3 仿真实验分析

3.1 数据集描述

本文采集杭州某供电公司某一路光纤复合架空地线(OPGW，optical power grounded waveguide)连续350天光功率数据来作为仿真实验数据，取前250天数据进行模型训练和优化；后100天数据用于测试模型预测效果。原始光功率数据如图5所示。

图5 光功率原始数据图

3.2 模型评价指标

本文预测模型效果的评价指标选用均方根误差(RMSE，root mean square error)其数学表达式为：

(20)

3.3 实验配置

本文全部的试实验全部在表1所给出的配置下进行。

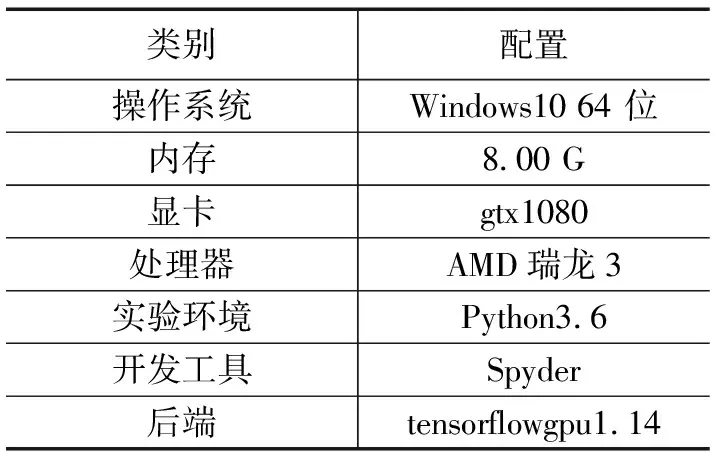
表1 实验设置表

3.4 FA-ARIMA-GRU 模型验证

3.4.1 数据预处理

数据预处理第一步需要对原始光功率数据进行分解与重构操作，而小波变换中不同的小波分解层数与小波基所得到的分解结果是不同的，故确定小波分解层数和选取恰当的小波基在小波变换应用中起到决定性作用。Coiflet、Daubechies、Haar、Symlets等是常用的几种小波基，其在不同的应用场景得到广泛的应用。

在对小波基选取的过程中，重点对相似性、消失矩、对称性、支撑长度和正则性这几点进行重点考虑。dbN小波在大量实际应用过程中呈现出高消失矩和较好正则性等优点，于此同时也暴露出其不具备对称性的缺陷，该缺陷可能致使信号在分析与重构过程当中出现相位失真的现象。symN小波在实际应用过程中较dbN小波具有较好的对称性，能够在一定程度减少相位失真现象的发生。对于小波分解的层数，信噪比不同的信号均有一个接近最优的分解层数，过多分级层数会导致信号严重失真；而分解层数过少会导致信号去噪效果较差，对后续信号的进一步分析造成一定程度的影响。

综上所述，本文选取sym1、sym2、sym3、sym4、db1、db2、db3、db4八种不同的小波基，对各小波基进行1～4层小波分解，并对分解后的小波进行重构，将最终数据代入至本文所构建的预测模型当中，将预测数据与原始数据进行对比，并对预测RMSE值进行计算，得到如表2所示数据。

表2 不同小波基函数与分解层数预测RMSE 值

由表1可知，原始光功率随着小波分解层数的不断提升，损失逐渐增多，致使预测误差不断增大，通过上述数据的对比，得出在一层小波分解当中运用 sym4小波基函数计算所得的结果RMSE最小，故本文选用 sym4 小波基函数对原始数据进行一层小波分解。

通过sym4小波基函数对上述采集获得的原始光功率数据进行一层分解和重构，经过分解与重构得到的光功率数据如图6所示。

图6 sym4小波处理后的数据图

3.4.2 实验结果分析

此节采用ARIMA-GRU预测模型和本文构建的FA-ARIMA-GRU预测模型在前期预留的100天电力光纤光功率测试数据集上进行预测结果和实际数据的对比，并以拟合曲线的方式来呈现不同预测模型所预测的效果，如图7所示。由图7可以看出，本文所构建的FA-ARIMA-GRU预测模型较ARIMA-GRU与原始更为接近，更能准确预测未来电力光纤光功率的发展趋势，从而提前掌握电力光纤的线路状态，为电力光纤故障定位提供可靠的参数依据，起到辅助作用。