On the Local Structure of C3-critical Minimally 6-connected Graphs*①

MO Fen-mei,LIANG Yu

(1.School of Mathematics and Statistics,Nanning Normal University,Nanning 530100,China；2.Nanning No.26 Middle School，Nanning 530022， China)

Abstract：A k-connected graph is minimal if G-e is no longer k-connected for every e∈E(G).S.A.Obraztsova shows that every vertex of minimally 6-connected graph adjacent to one vertex of degree 6.A C3-critical minimally 6-connected graph is a minimally 6-connected graph in which every complete subgraph on at most 3 vertices is contained in a 6-separator.Let G be a C3-critical minimally 6-connected graph,and let G6 stand for the subgraph of G induced by the set of vertices of degree 6.This paper shows that every component of G6 has at least four vertices and has a vertex of degree at least three.

Key words：minimally 6-connected;C3-critical;structure

0 Introduction

For any graphG,let V(G) and E(G) denote the vertex set and edge set ofG, respectively.IfX⊆V(G), let NG(X)={y∈V(G)-X：yx∈E(G) for somex∈X}.Members of NG(X) are neighbors ofXand the set NG(X) is the neighborhood ofX.For anyx∈ V(G), we will write NG(x) for NG({x}).As usual,|NG(x)| is the degree ofx,which is denoted by dG(x).Let EG(x) stand for the set of edges ofGthat are incident withx.We will drop the subscriptGif there is no need to emphasizeG.

A graphGis a criticalk-connected graph ifκ(G)=kand every vertex ofGis contained in a smallest separator.An edgeeof ak-connected graphGis said to bek-contractible ifG/eis againk-connected,otherwise we said thateis non-contractible.Ak-connected graph withoutk-contractible edge is called a contraction criticalk-connected graph.Observe that an edgexyof a non-completek-connected graphGis non-contractible if and only ifGhas a smallest separator containing bothxandy.

Notice that everyK1subgraph of a criticalk-connected graph is contained in ak-separator,and everyK2subgraph of a contraction criticalk-connected graph is contained in ak-separator.W.Mader[1]generalized this observation,he introduced the definition ofCm-critical graph.A connected graphGisCm-critical if every complete subgraph ofGon at mostmvertices is contained in a smallest separator.Further,a connected graphGis aC-critical if every complete subgraph ofGis contained in a smallest separator.W.Mader[1]prove the following theorem.

Theorem0.1[1]EveryC3-critical graph is 6-connected,and everyC-critical graph is 8-connected.

LetGbe ak-connected graph with |V(G)|≥k+2.An edgeeofGis said to bek-removable ifG-eis stillk-connected.Ak-connected graphGis a minimallyk-connected ifGcontains nok-removable edge.Lete=xybe an edge of minimallyk-connected graphG, thenG-ehas ak-1 separatorTwhich separatesxandy.Further,we see thatG-xy-Tconsists of exactly two connected components: one of them containsx, the other one containsy.Ak-connected graph isCm-critical minimal graph ifGis bothCm-critical and minimalk-connected.S.A.Obraztsova[2]showed the following theorem.

Theorem0.2[2]Every vertex of a minimally contraction-critically 6-connected graphGhas a neighbor of degree 6.

Clearly,aC3-critical minimally 6-connected graph is a minimal contraction-critically 6-connected graph.Hence,every vertex ofC3-critical minimally 6-connected graph has a neighbor of degree 6.Let V6(G) stand for the set of all vertices of degree 6,and letG6=G[V6(G)].A.V.Poster[3]shows the following theorem holds.

In [4],it is shown that every vertex ofGhas two neighbors of degree 6,which implies the result of A.V.Poster.

Theorem0.4[4]LetGbe aC3-critical minimal 6-connected,then every vertex ofGadjacent to two vertices of degree 6.

This paper focuses on the local structure ofG6,we have the following results.

Theorem0.5 LetGbe aC3-critical minimally 6-connected,then every component ofG6has at least four vertices.

Theorem0.6 LetGbe aC3-critical minimally 6-connected,then every component ofG6has a vertex of degree at least 3.

1 Some Lemmas

In this section we present a few lemmas which will be used in the proof of the main results.The following properties of fragments are well known (for the proof see [1],we will use them without any further reference.

Lemma1.1[1]LetGbe ak-connected graph,and letSbe a set of subsets of V(G).LetFandF′ be two distinct fragments with respect toS,and letT=N(F),T′=N(F′).If (F′∩T)∪(T′∩T)∪(F∩T′) contains a member ofSthen the following statements hold.

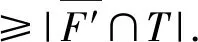
Lemma1.3[4]LetAbe a fragment of ak-connected graphG, and letS⊆N(A).If |N(S)∩A|< |S| thenA= N(S)∩A.

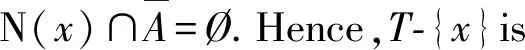
Lemma1.5 LetGbe a contraction criticallyk-connected graph,A={x,y} is a fragment ofG.LetBbe a fragment with respect toxz, wherez∈N(A).If N(A)-{z}⊆N(y), thenA⊆N(B).

ProofSupposeAN(B).Without loss of generality,lety∈A∩B.Then we can see thata contradiction.This contradiction assures us thatA⊆N(B).

Lemma1.6[5]LetGbe a minimallyk-connected.ThenG-Vk(G) is a forest.

Lemma 1.6 assures us that every cycle of minimallyk-connected graph has a vertex of degreek.

Lemma1.7[4]LetGbe aC3-critical minimally 6-connected graph,A={x,y} be a 2-fragment andT=N(A)，then

(1) d(x)=6 or d(y)=6;

(2) If d(x)=7,d(y)=6,then every vertex in N(y)∩Tis degree 6.

Lemma1.8[4]LetGbe aC3-critical minimally 6-connected graph.IfA={a,b} is a 2-fragment,xy∈E(G) and {x,y}⊆N(A), then either d(y)=6 or N(x)∩A∩V6(G)≠Ø.

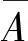
2 A proof of theorem 0.5

Claim1 |A|≥3.

If |A|=1 then,sinceA∩{x,y,z}=Ø,xadjacent to three vertices of degree 6,a contradiction.Hence,we may assume that |A|≥2.Suppose that |A|=2.By Lemma 1.8,we see that eitherx1has degree 6 or N(x)∩A∩V6(G)≠Ø.It follows thatxadjacent to three vertices of degree 6,a contradiction.So we may assume that |A|≥3.

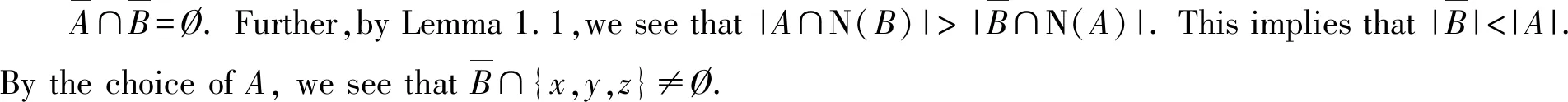
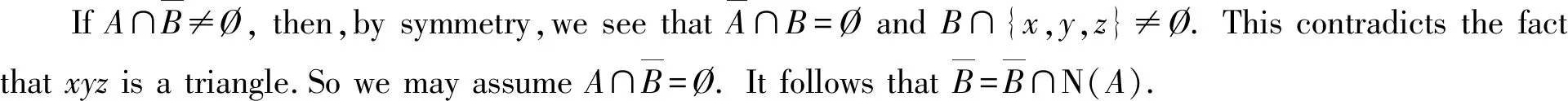
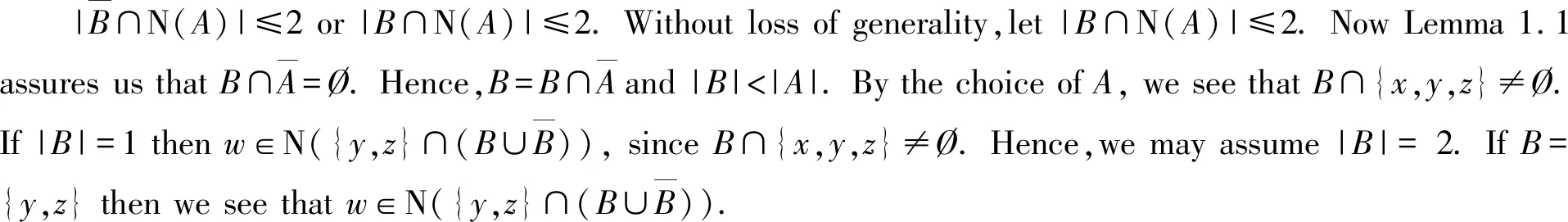
By Claim 3,N(x)∩A⊆N(y)∪N(z).

Claim4 N(x)∩A⊆N(y) and N(x)∩A⊆N(z).

Letw∈N(x)∩A.By Claim 3,we may assume thatw∈N(y).Now we see thatwxyis a triangle.LetBbe a fragment ofGsuch that {w,x,y}⊆N(B).Sincey∈N(B), Claim 3 assures us thatw∈N(z).

By Claim 4,we see that {y,z}⊆N(A).

Claim5 |N(x)∩A|≥2.

Suppose |N(x)∩A|=1.Let N(x)∩A={w} andA′=A-{w}, now we see that {y,z}∈N(A′) andw∈N(A′).Further,by Claim 4,yw∈E(G).It follows thatA′ is anS- fragment,which contradicts the choice ofA.

Claim6 |N(y)∩A|≥3 and |N(z)∩A|≥3.

Suppose |N(y)∩A|=2.By Claim 5,we see that |N(x)∩A|=2.By Claim 3,we see that N(x)∩A⊆N(y) and N(x)∩A⊆N(z).It follows that |N({x,y})∩A|=2.LetA′=A-N({x,y}).It follows thatA′ is a fragment such that N(A′)=N(A)∪(N({x,y})∩A)-{x,y}.Now we see thatz∈N(A′) and N(z)∈N(A′)-{x,z}≠Ø.It follows thatA′ is anS-fragment,which contradicts the choice ofA.So we see that |N(y)∩A|≥3.Similarly,|N(z)∩A|≥3.

3 A proof of theorem 0.6

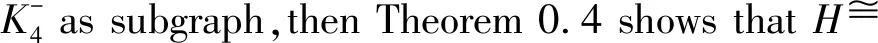
By symmetry,the following claim holds.

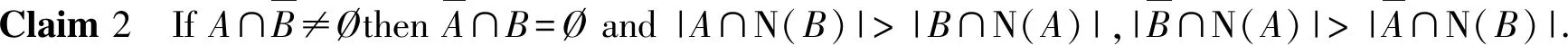
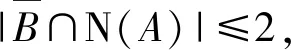
Lemma3.2 LetGbe aC3-critical minimally 6-connected graph,Hbe a component ofG6such that every vertex ofHhas degree 2.LetS={{a,b}|ab∈E(H)} then everyS-fragment has at least three vertices.

ProofLetAbe anS-fragment,let {a,b}⊆N(A) and {a,b}∈s.If |A|=1, sayA={c}, thenHis a triangle,a contradiction.So we may assume |A|=2, sayA={u,v}.Without loss of generality,letu∈N(a).Ifu∈N(b), then Theorem 0.4 assures us that d(u)=7.Now Lemma 1.7 assures us that d(v)=6.Further,N(A) has at least five vertices of degree 6 andvadjacent to at least four vertices of degree 6.Hence,v∉H.It follows thatv∉N({a,b}).It follows that N({a,b})∩A={u}.Now Lemma 1.3 assures us that |A|=1, a contradiction.Hence,both vertices ofAhave degree 6.It follows thatA⊆V(H) andHhas exactly four vertices.Now Lemma 3.1 shows thatHhas at least one vertices which has degree 3,a contradiction.Hence,everyS-fragment has at least three vertices.

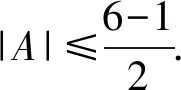
Without loss of generality,let {x1,x2}⊆N(A).Lety1∈N(x1)∩A.LetHmbe a complete graph that containsx1y1such that V(Hm)⊆V(H)∪{y1} andm≤3.Further,we choosem=3 if it is possible.LetBbe fragment such that V(Hm)⊆N(B).

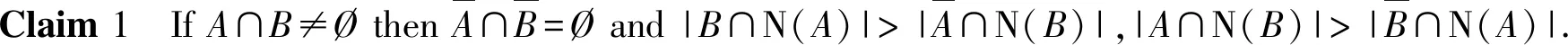
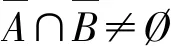
By symmetry,the following claim holds.