基于Ansys的PC梁力学性能及非线性分析

周国贤，蒋一辉

(北京市建设工程质量第三检测所有限责任公司，北京 100037)

1 理论计算

桥梁的极限状态分为承载能力极限状态和正常使用极限状态，预应力混凝土结构的正常使用状态与设计张拉应力有关，同时还需满足反拱及截面上缘应力的要求。对PC梁的极限状态的计算方法和验算内容均取自规范[8]。采用直线布筋和粘结预应力筋形式，混凝土强度等级C50，偏心距50 mm，矩形截面，外观尺寸为200 mm×300 mm×3 000 mm。材料参数值均取自规范[8]。PC梁作为受弯构件，承载能力极限状态计算内容为抗弯承载力和极限荷载。正截面抗弯承载力采用规范[8]中方法计算，计算结果为：Mu=76.03 kN·m，采用三分点加载，极限荷载为：Nu=152.06 kN。

极限状态理论计算结果表明，承载能力极限状态与预应力大小无关，正截面抗弯承载力为76.03 kN·m，极限荷载为152.06 kN。正常使用极限状态与预应力大小相关，设计张拉力为180 kN时，满足全预应力混凝土构件的要求，该条件下，反拱和上缘验算均满足要求。

2 建立分析模型

本模型采用实体力筋法建立预应力筋，降温法模拟预应力。混凝土采用SOLID65单元。混凝土的受压应力-应变关系采用公式(1)计算[9]：

(1)

式中：x为应变/受压峰值应变；y为应力/峰值应力；αa和αd为采用试验结果的回归式计算值[9]。

考虑使用力加载，故混凝土应力-应变曲线中暂不考虑下降段，其受压应力-应变曲线如图1(a)所示。钢筋采用link180杆单元，预应力筋屈服强度1 260 MPa，普通钢筋屈服强度280 MPa。

为避免预应力导致端部混凝土局部承压过早开裂，在相应区域设置了两个钢垫板，与预应力筋和混凝土用节点耦合法进行连接，材料特性与普通钢筋相同。

2.1 极限荷载求解

PC梁加载方式选择三分点加载，即跨中1 000 mm范围内为纯弯段，两侧为剪弯段。考虑避免应力集中在加载点处设置垫板，将集中力换算为面荷载施加在结构上，垫板尺寸为200 mm×200 mm。

(1)施加预应力阶段：施加预应力180 kN，将其带入温度计算公式，得到降温数值为-274.7 ℃。分级张拉完成后结构会有一定的反拱。PC梁施加预应力后计算结果，梁上拱最大值为0.468 mm，除去锚固区的一个梁高范围(圣维南原理)，混凝土全截面受压。压应力最大和最小值分别为4.84 MPa和0.33 MPa。

(2)施加外荷载阶段：施加预应力后，逐步添加外荷载。当外荷载达到160 kN时，PC梁变形出现不收敛，此时PC梁的跨中竖向位移达到32.347 mm，纯弯段的受压区混凝土应力也已经达到抗压强度。

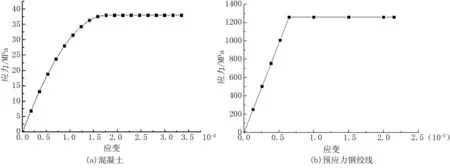
图1 Ansys材料应力-应变曲线

2.2 极限荷载分析

跨中荷载—位移曲线呈现明显的四阶段特性，如图2所示：第Ⅰ阶段为弹性未开裂；第Ⅱ阶段为裂缝发展直到普通钢筋屈服；第Ⅲ阶段为普通钢筋屈服到预应力筋屈服；第Ⅳ阶段为预应力筋屈服至结构破坏。

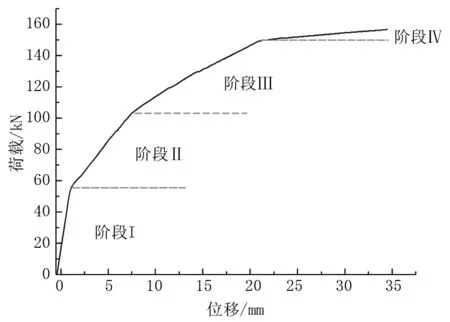
图2 荷载—位移曲线

荷载—位移曲线有3个突变点分别对应不同阶段，随着荷载增大斜率逐渐减小，表明各阶段的刚度逐渐降低，而各阶段内荷载与位移近似线性发展。

3 阶段分析

3.1 PC梁弹性阶段

PC梁弹性阶段跨中截面荷载—位移曲线如图3所示，施加预应力后，结构竖向反拱值为-0.420 mm，施加荷载60 kN后，结构竖向位移为0.875 mm。可以看出，跨中截面位移与荷载呈线性关系，且无突变或转折点，即结构刚度无明显变化，结构不存在材料性能退化和损伤。

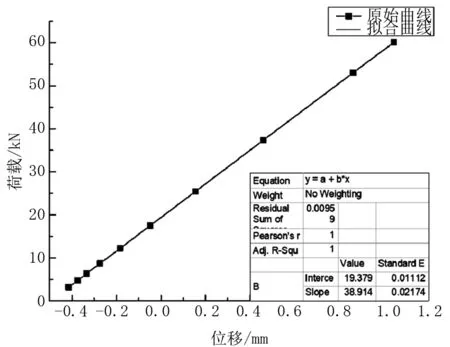
图3 跨中截面荷载—位移曲线

弹性阶段的刚度可由结构力学图乘法求得。刚度表达式为

(2)

式中：EI为桥梁结构静刚度(其中E为混凝土弹性模量，I为截面惯性矩)；L为桥梁计算跨度；P为集中荷载；Uy为跨中截面竖向位移。

采用线性拟合方法统计荷载与位移的关系为

P=38.914uy+19.379

(3)

拟合公式中uy为跨中截面竖向位移，其余参数含义同式(2)。

方程的斜率为38.914，截距为19.379。带入结构刚度计算公式中，得到此时PC梁的刚度

(4)

预应力筋张拉完成后，跨中截面上缘应力为0.60 MPa，跨中截面下缘应力为5.06 MPa，全截面受压。弹性荷载施加后，跨中截面上缘应力为8.34 MPa，上缘受压，跨中截面下缘应力为-3.01 MPa，下缘受拉且未达抗拉强度，截面未开裂，结构处于弹性工作状态。

综合以上分析，在开裂荷载60.09 kN作用下，结构处于弹性阶段，该刚度为结构无损阶段的刚度，可作为结构的初始刚度使用，开裂损伤后的PC梁刚度下降对比分析均以此值为基础。

3.2 裂缝发展阶段

荷载—位移曲线的第Ⅱ阶段，裂缝开始发展直到受拉区普通钢筋屈服，外荷载可达到105 kN，该阶段荷载—位移曲线如图4所示。该阶段初期裂缝发展迅速，之后逐渐稳定，裂缝高度可达0.67 h；预应力钢绞线的应力增长速率将大于截面开裂前。由于截面开裂高度在荷载作用下不断增大，截面的刚度也在不断降低，说明PC梁进入非线性阶段。此阶段混凝土弹性模量已开始下降，应力-应变关系可采用公式(1)描述，其曲线斜率的变化表征弹性模量的降低速率，但总体上变化量值很小。

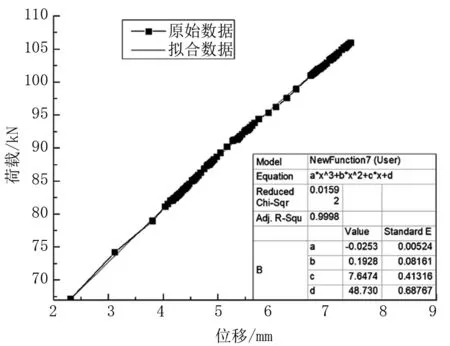
图4 开裂阶段荷载—位移曲线

在分析该阶段刚度时，在原始荷载—位移曲线基础上采用线性拟合的方法与原数据相差较大，尤其是在初始阶段；而且由荷载与应力的正相关关系可知，结构刚度EI的变化应采用二次多项式拟合，荷载—位移曲线的斜率表征刚度的变化率，所以荷载位移曲线可采用三次多项式拟合。荷载—位移拟合曲线方程为

(5)

根据荷载—位移曲线方程求得曲线斜率方程为

(6)

式中：K为拟合刚度。

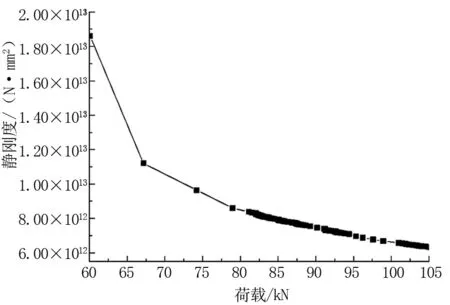
图5 刚度下降曲线

刚度下降曲线如图5所示，取图中数据线性插值可以求得任意荷载下的结构刚度，表1列出了裂缝发展阶段6个具有代表性的裂缝高度和刚度。可以看出，此阶段由于裂缝高度和范围前期增长较快，导致梁刚度前期下降很快；随着荷载增加，裂缝高度和范围发展逐渐减速，梁刚度下降速率逐渐降低；此阶段的结构刚度整体下降了64.11%，所以此阶段刚度下降比率最大。

3.3 普通钢筋屈服到预应力筋屈服阶段

第Ⅲ阶段裂缝继续扩展直到预应力钢筋屈服。该阶段裂缝高度从0.67倍的梁高发展到0.72倍的梁高，扩展量较小；而由混凝土应力-应变关系式(1)可知，此阶段压区混凝土弹性模量逐渐退化，会导致裂缝宽度增大，预应力钢绞线的应力增长加快，上述现象综合表明梁已经进入了弹塑性阶段。

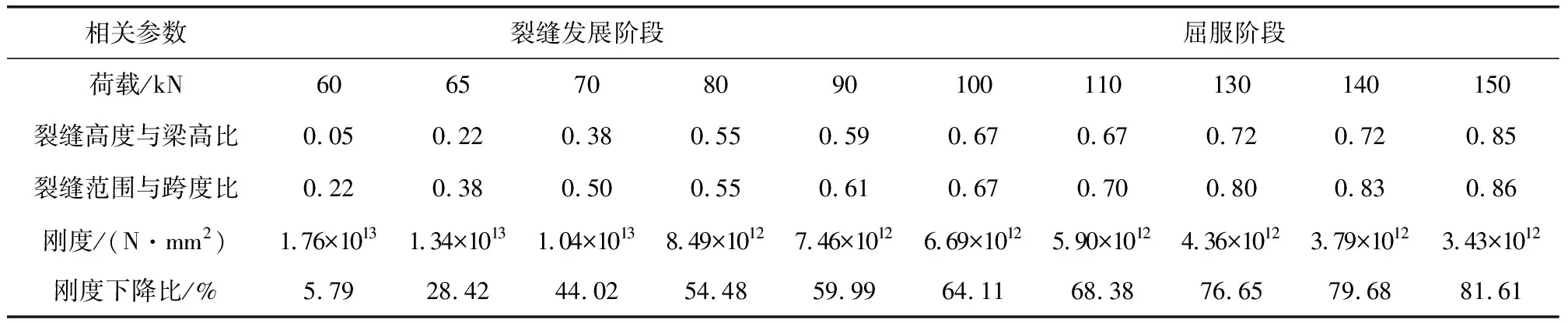
表1 裂缝发展阶段与屈服阶段裂缝特征与刚度变化

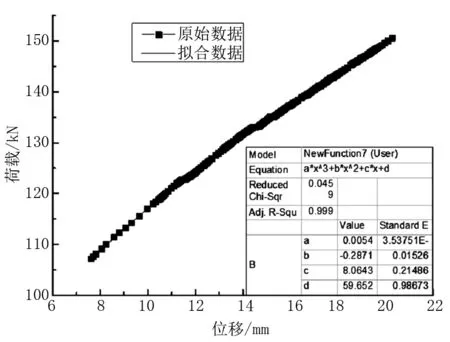
图6 屈服阶段荷载—位移曲线

在计算刚度时，采用非线性拟合的曲线与原始曲线误差较小，可以用于该阶段的刚度分析。拟合曲线方程如下

(7)

根据荷载—位移曲线方程求得曲线斜率方程为

(8)

由计算公式(2)同样可以计算出不同裂缝高度的刚度，表1列出了四个代表性的裂缝特征和刚度。可以看出，随荷载增加，刚度下降量值很大，预应力钢筋临近屈服时达到了81.61%；但刚度下降比率较小，与上一阶段相比较下降了17.50%。

通过以上分析可知，由于此阶段裂缝高度和范围扩展相对减缓，而压区混凝土弹性模量退化，所以该阶段刚度降低是由裂缝扩展和压区混凝土弹性模量退化综合造成的。

另外，当预应力筋屈服后，即荷载—位移曲线的第Ⅳ阶段，继续加载量值很小时，梁变形会持续增大而失稳破坏；只有采用应变加载方式，才能获得预应力筋屈服后的荷载—位移关系，由于此项研究内容往往是桥梁抗震研究的重点，服役混凝土桥梁极少达到此阶段，不属于本文研究范畴，所以不再赘述。

4 结 论

PC梁静力加载过程呈现明显的四阶段特征：弹性阶段刚度基本不变；开裂阶段刚度非线性下降，相比弹性阶段，刚度下降了64.11%，同时裂缝迅速开展，达到0.67倍的梁高；受拉区普通钢筋屈服后， 刚度仍然按非线性下降， 此时刚度下降量值很大，预应力钢筋临近屈服时达到了81.61%，裂缝发展至0.85倍的梁高；预应力筋屈服后，裂缝快速开展到一定程度后趋于稳定，直至混凝土被压碎。与某简支T梁实桥承载能力试验结果[2]相比，由于存在截面形式、尺寸效应和布筋形式等差异，模型计算结果中关于简支梁刚度下降及裂缝高度的具体数值与实桥试验结果的误差在±10%左右，实际桥梁由于受到设计、施工和运营各个阶段的影响，试验结果与模型结果之间的误差在可接受范围之内。