脉冲氙灯加热高性能热塑性复合材料工艺参数分析*

靳子昂，韩振宇，李品华，刘旭黎，孙守政，2，富宏亚

（1. 哈尔滨工业大学机器人技术与系统国家重点实验室，哈尔滨 150001；2. 哈尔滨工业大学芜湖机器人产业技术研究院，芜湖 241007）

纤维增强树脂基复合材料相比于传统金属材料具有轻质、高强、抗疲劳、耐腐蚀和性能可设计等优点，被广泛地应用于航空航天、交通和能源等领域[1–3]。根据树脂基体性质的不同，又可分为热固性和热塑性复合材料[4]。相比于热固性复合材料，热塑性复合材料不仅具有较高的抗冲击损伤能力[5]，还具有良好的耐高温、耐腐蚀和可焊接性能[6]。同时，热塑性复合材料可以在室温下储存，拥有更长的储存周期。此外，当热塑性复合材料被加热时发生的是物理变化，可回收利用反复加工[7]。然而，由于热塑性复合材料具有高熔点和高黏性的特点，因此对其成型工艺提出了更高的要求，成型工艺也更加复杂。此外，高昂的原材料、设备和技术成本也严重限制了热塑性复合材料的大量应用。

自动铺丝作为树脂基复合材料自动化成型技术之一，结合了纤维缠绕和自动铺带的优势，可成型大曲率、复杂曲面和变刚度构件[8–9]。但是，高性能热塑性复合材料熔点较高且加工工艺窗口窄，增加了自动铺丝的铺放难度。目前，自动铺丝技术采用的加热方式主要有热风、红外和激光等[10–15]，每种加热方式各有其优缺点。热风加热的优点是成本低且安装灵活，但是缺点为升温与降温速率慢，使得成型效率低，且热流不稳定，导致能量的利用率低，造成能源的浪费。Qureshi等[16]研究了热风加热CF/PEEK预浸料的工艺参数与力学性能的关系，结果表明，不稳定的热流是目前热风加热的一个严重问题，该问题限制了铺放速度的提高，导致生产效率降低且层合板的力学性能较低。Tafreshi[17]和Zacherl[18]等研究了热空气与CF/PEEK预浸料之间的对流传热系数对传热机理的影响，结果表明，对流传热系数取决于包括喷嘴的几何形状、基板表面的状态、热气流的类型、温度和速度在内的各种参数，而对流传热系数在加热过程中并不稳定。对于红外加热，其通过热辐射对材料进行加热，但是加热温度较低，通常用于加热熔点较低的复合材料。Venkatesan等[19]使用红外加热辅助自动铺丝成型树脂熔点为220 ℃的CF/PA预浸料，结果表明，通过工艺优化制造的层合板缺陷较少，力学性能较好。激光加热具有极快的升温、降温速率和较高的功率，是高性能热塑性复合材料成型比较理想的加热方式之一。Chanteli[20]和Kollmannsberger[21]等使用激光加热CF/PEEK 预浸料，结果表明，激光可以在短时间内熔化树脂，通过工艺优化实现快速铺放且层合板具有良好力学性能。

尽管激光是目前加热高性能热塑性复合材料最好的加热方式之一，但是也存在以下缺点，如前期投入成本较高、空间体积较大、具有一定的安全问题且难以控制光束末端的位置精度等。而近几年出现的脉冲氙灯加热方式不仅具有与激光相媲美的升温、降温速率，而且其光源波段很宽，包含了紫外光、可见光和红外光，这种宽波段光源使用安全，无须激光防护罩，操作人员可以近距离操作，易于扩展以满足不同的加热宽度要求，同时有利于碳纤维的高水平吸收。此外，灯头尺寸小巧、安装方便且相比激光成本较低，有望在未来成为自动铺丝激光加热的替代热源。但目前还没有相关文献报道关于脉冲氙灯作为自动铺丝的加热方式，脉冲氙灯加热高性能热塑性复合材料的工艺参数也是未知。因此，研究脉冲氙灯加热高性能热塑性复合材料的可行性和工艺参数优化对于自动铺丝成型热塑性复合材料构件的发展具有重要意义。

本文采用单因素试验和响应面法研究了脉冲氙灯各参数对高性能热塑性复合材料加热温度的影响规律，以及各参数之间的交互作用影响规律，并提出了相应的工艺参数优化顺序，为自动铺丝成型高性能热塑性复合材料构件的后续研究工作提供参考。

1 试验材料与装置

分别准备了3种热塑性预浸料：CF/PEKK（中国科学院宁波材料技术与工程研究所）、CF/PEEK–1（荷兰Tencate公司）和CF/PEEK–2（黑龙江英创新材料有限公司），其材料参数见表1。利用NewView 8200型白光干涉仪 （美国，ZYGO公司）对3种预浸料的三维表面形貌和表面粗糙度进行测试分析。在3种预浸料表面某一区域沿纤维方向从上到下分别测试3条线粗糙度 （图1），计算这3条线粗糙度的平均值以表征其面粗糙度，得到CF/PEKK、CF/PEEK–1、CF/PEEK–2共3种预浸料的平均表面粗糙度分别为2.66 μm、1.46 μm和24.93 μm （表1）。由表1和图1可知，对于CF/PEKK和CF/PEEK–1两种预浸料，其表面平整光滑，表面粗糙度较小，而CF/PEEK–2预浸料的表面粗糙度较高。

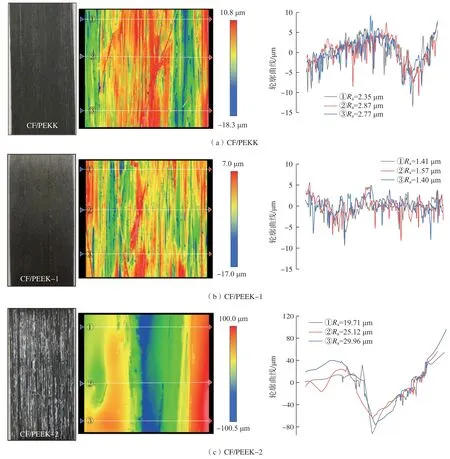
图1 3种热塑性预浸料的表面形貌和表面粗糙度Fig.1 Surface morphology and surface roughness of three kinds of thermoplastic prepregs

表1 3种热塑性预浸料的参数Table 1 Parameters of three kinds of thermoplastic prepregs

热塑性复合材料在自动铺丝成型过程中是否熔化，主要与加热温度和热源移动速度有关，与铺放压力的关系较小 （铺放压力主要影响树脂熔化后的变形），因此本文搭建的试验装置忽略了铺放压力。图2是脉冲氙灯加热热塑性复合材料的测试过程示意图，将热塑性预浸料放置在测试平台上，并用耐高温胶带固定两端。Humm3TM型脉冲氙灯由德国贺利氏 （沈阳）特种光源有限公司提供，其波长覆盖紫外光、可见光和红外光。通过在测试平台上将脉冲氙灯沿着预浸料的纤维方向移动进行加热。红外测温热成像仪（德国，MCRO-EPSILON公司）固定在测试平台的另一端，测量加热过程中预浸料表面的温度，并将峰值温度作为加热温度。

图2 脉冲氙灯加热热塑性复合材料测试过程示意图Fig.2 Schematic diagram of testing process for thermoplastic composites heated by pulse xenon lamp

2 单因素试验分析

影响脉冲氙灯加热塑性复合材料的因素包括脉冲氙灯的电压U、脉冲频率F、脉宽W、灯口与预浸料之间的距离D、热源的移动速度S。根据脉冲氙灯厂商工程师建议，通常脉冲频率F选择60 Hz，灯口与预浸料的距离D选择10 mm。因此，影响脉冲氙灯对热塑性预浸料加热温度T的影响因素主要为电压、脉宽和热源移动速度。

通过单因素试验分别研究了电压、脉宽和热源移动速度对CF/PEKK、CF/PEEK–1和CF/PEEK–2预浸料加热温度的影响。试验过程中发现CF/PEEK–2预浸料在同一工艺参数下，加热温度不稳定，波动很大（图3（a））。根据脉冲氙灯的加热原理，利用储存的电能或化学能在极短时间内发生高功率、高强度闪光，以电磁波的形式传递能量。由于 CF/PEEK–2预浸料的表面粗糙度值较大，对脉冲能量的吸收能力不均匀，导致加热温度的差异较大，因此无法用于后续工艺参数对加热温度的影响规律。而CF/PEKK和CF/PEEK–1预浸料表面粗糙度值小，其加热温度稳定。同时，获得了电压、脉宽和热源移动速度对加热温度的影响规律 （图3（b）～（d））。当脉宽和热源移动速度一定时，加热温度随着电压的增加而升高。同样，加热温度随着脉宽或热源移动速度的增加而降低。根据脉冲氙灯峰值功率P定义，即

P=E/t

式中，E代表脉冲能量；t代表脉宽。由于脉冲氙灯的加热原理是将电能转化为内能，所以当增大电压时，可以获得较高的脉冲能量，进而增大峰值功率，加热温度因此升高。同时，由峰值功率定义可知，脉宽与峰值功率成反比，增加脉宽则会降低峰值功率，加热温度因此降低。对于热源移动速度对加热温度的影响，随着热源移动速度的增加，脉冲氙灯在预浸料表面的停留时间较短，导致加热时间短，故加热温度降低。

3 响应面法分析

3.1 响应面试验结果

响应面法是利用多元回归方程拟合响应因子与响应值之间的函数关系，通过分析响应面等值线探寻最优工艺参数的一种统计方法[22]。根据第2节单因素试验结果，脉冲氙灯对CF/PEKK和CF/PEEK–1两 种 预浸料的加热温度稳定且影响规律一致。因此，下文仅以CF/PEEK–1为研究对象，基于响应面法研究电压、脉宽和热源移动速度对加热温度的交互作用影响规律。对于CF/PEEK–1预浸料，其加热温度区间一般为340～400 ℃[23]。 因此，各响应因子水平如表2所示。

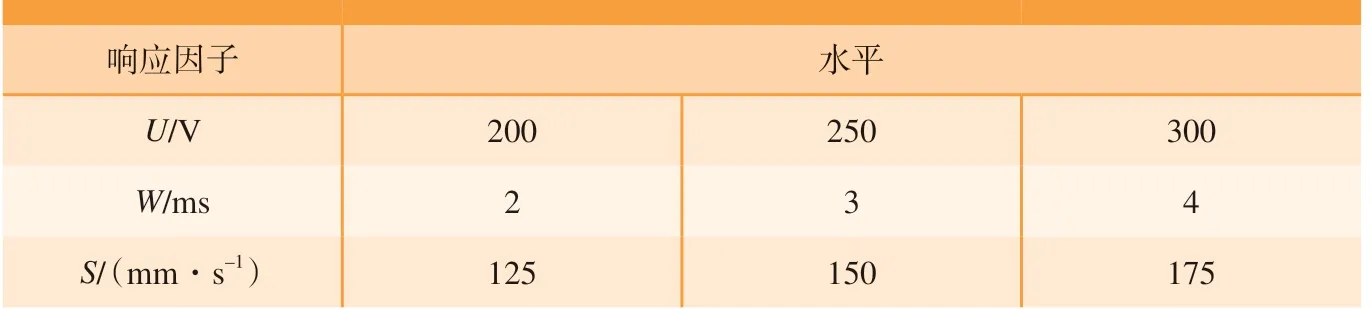
表2 响应因子水平表Table 2 Level table of response factors

采用中心组合试验设计得到17组试验，其试验结果如表3所示。可以看到，在所选响应因子范围内对CF/PEEK–1预浸料的加热温度范围为239～401℃。加热温度的分布范围很大，表明响应因子之间的合理匹配对CF/PEEK–1预浸料的加热温度影响较大。

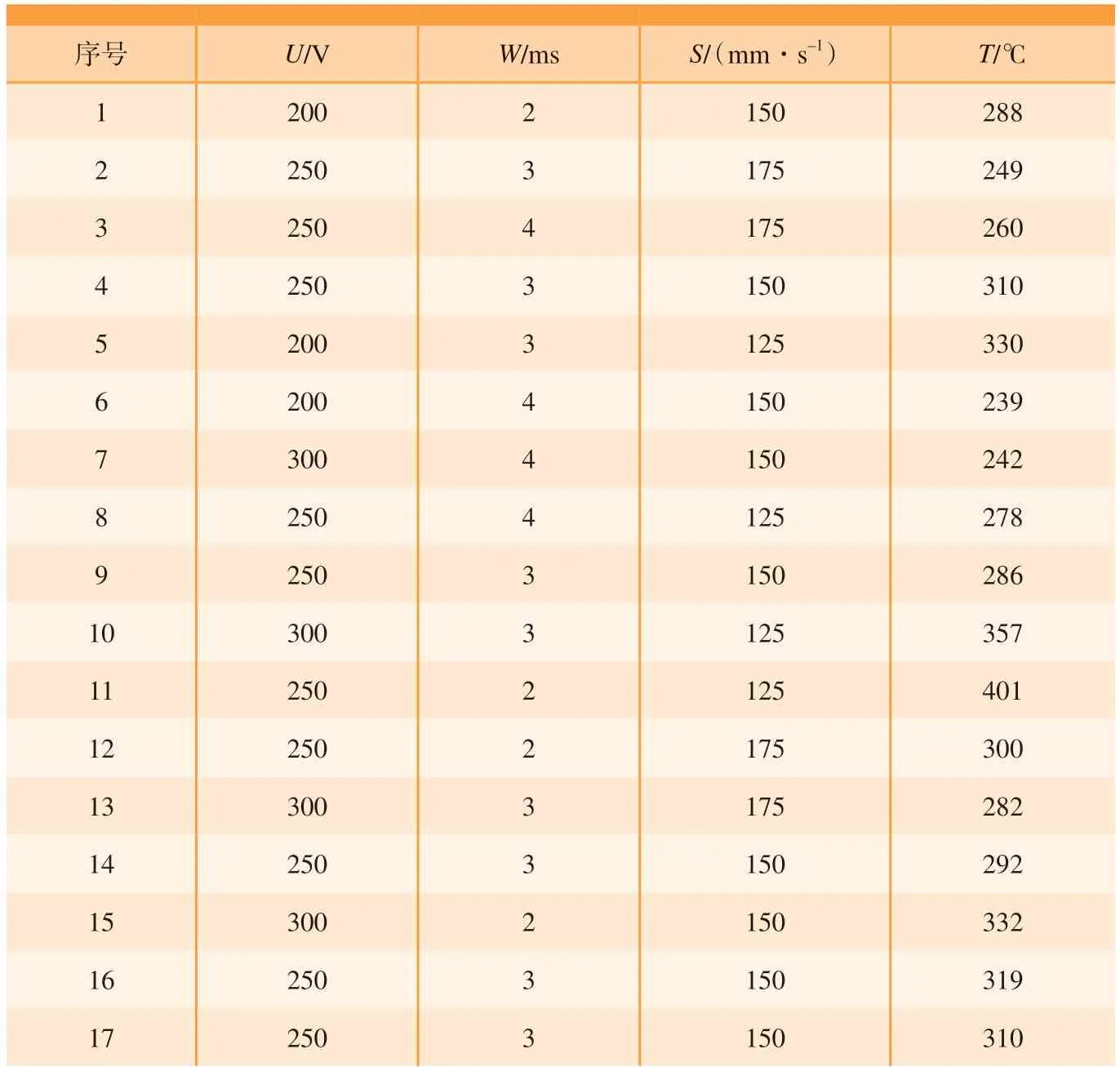
表3 响应面法试验结果Table 3 Response surface method test results

3.2 模型拟合分析

对于CF/PEEK–1预浸料加热温度的试验结果有4种拟合模型：线性模型 （Linear）、双因素模型 （2FI）、二次方程模型 （Quadratic）和三次方程模型 （Cubic），这4种模型拟合的结果如表4所示。可以看出，线性和二次方程模型的显著性p值均小于 0.05，说明上述两种模型的响应因子与响应值之间具有较强的相关性。二次方程模型的失拟度F值最大 （F= 0.7242），表明该模型的误差更小。同时，二次方程模型的决定系数（R2= 0.9638）接近于1，与调整决定系数（= 0.9173）接近，说明模型对试验理论数据做出了良好调整。综上所述，选择二次方程模型拟合结果。

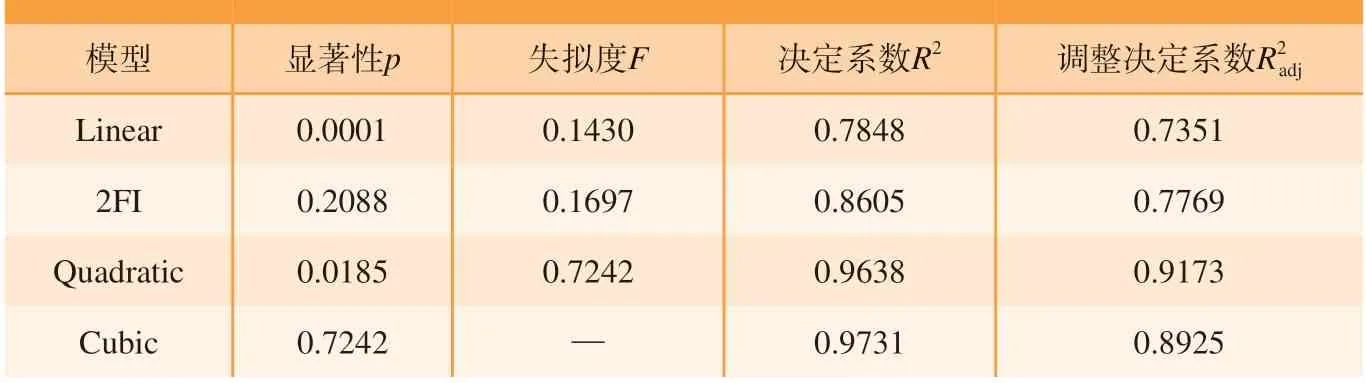
表4 4种模型拟合结果Table 4 Fitting results of four models

根据二次方程模型拟合得到3个响应因子U、W和S，T的回归方程为

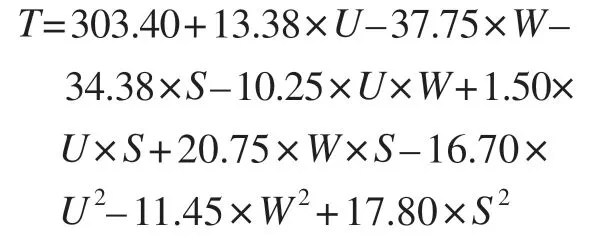
从方程系数中可以看出，3个响应因子单独对加热温度的影响大小依次为W>S>U，即脉宽对加热温度的影响最大，电压对加热温度的影响最小。3个响应因子对加热温度的交互作用影响大小依次为W–S>U–W>U–S，即脉宽和热源移动速度对加热温度的交互作用影响最大。

表5是加热温度二次方程模型的方差分析。可以看出，二次方程模型的F值为20.72，p值0.0003小于0.001，表明存在小于0.03%的可能噪声，这意味着电压、脉宽和热源移动速度对加热温度有显著的影响。同时失拟度F值为0.46，p值0.0558大于 0.05，说明所得方程与实际拟合的非正常误差比例较小，回归方程是可信的。模型中W和S的p值均小于0.0001，表明脉宽和热源移动速度对加热温度的影响非常显著，而U的p值为0.0168，介于0.001和0.05之间，表明电压对加热温度的影响是一般显著的。在响应因子交互作用项中，模型中W–S的p值为0.0111，小于0.05，说明脉宽和热源移动速度对加热温度的交互作用影响比较显著，而U–W和U–S的p值均大于0.05， 表明电压与脉宽、电压与热源移动速度对加热温度的交互作用影响不显著，这与回归方程中各系数的分析结论一致。

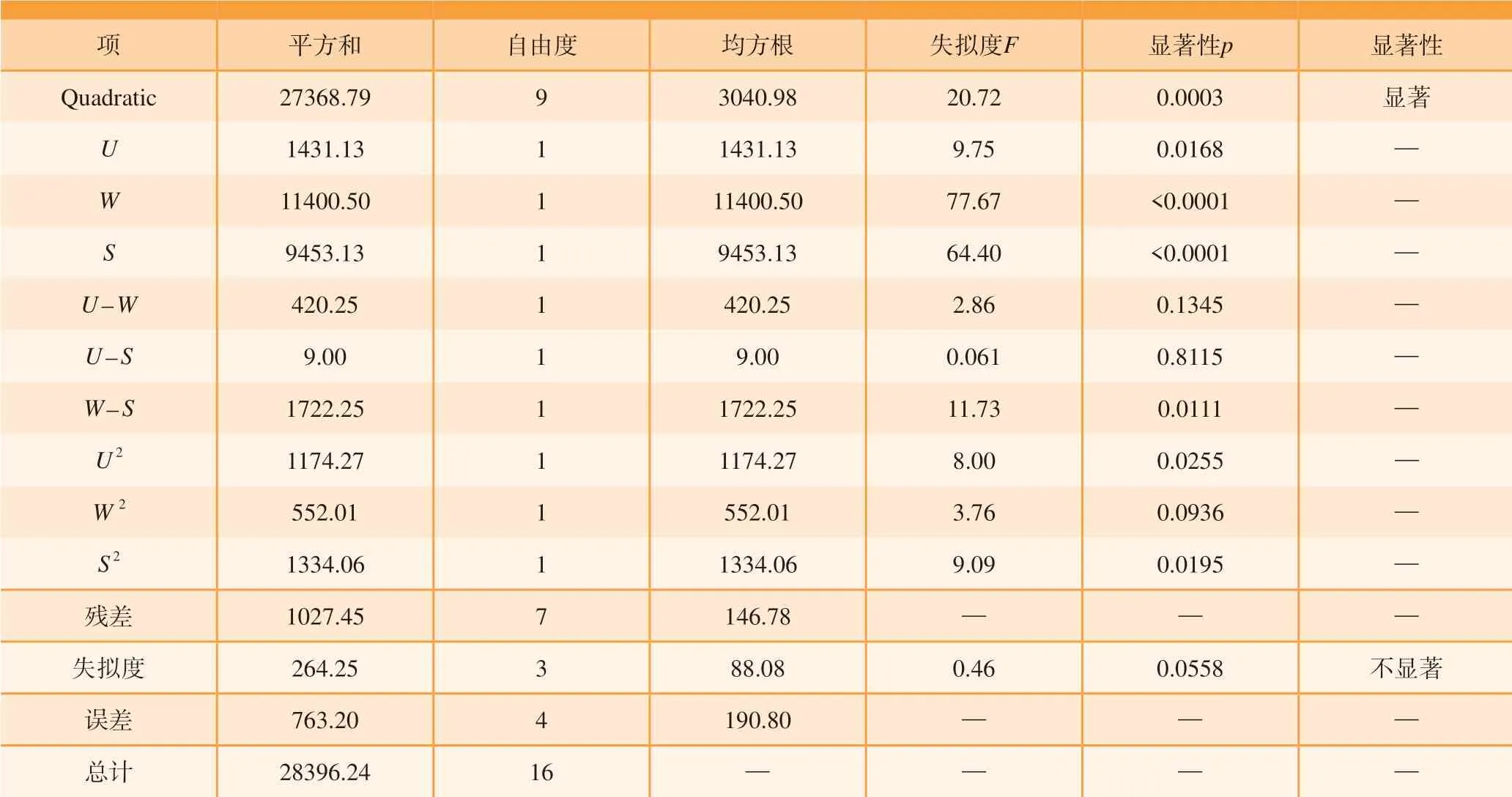
表5 加热温度的二次方程模型方差分析Table 5 Variance analysis of quadric model for heating temperature

根据回归模型的Studentized残差正态概率分布，实际值与预测值的对应关系以及Studentized残差与预测值的对应关系图中的散点分布情况可以推断模型是否合适。如果Studentized残差正态概率分布图中的散点接近线性，实际值与预测值的对应关系也呈线性则表示模型合适。Studentized残差与预测值对应关系图中的点分布散乱没有规律则模型合适[24]。从图4（a）和（b）可以看出，Studentized残差正态概率分布图中的点和实际值与预测值对应关系图中的点均呈线性分布，没有发现异常值的存在，说明加热温度的预测值与实际值之间的误差较小。从图4（c）Studentized残差与预测值的关系图可以看出，散点分布不规则，表明无异常结构模型，进一步验证了模型的适合性。

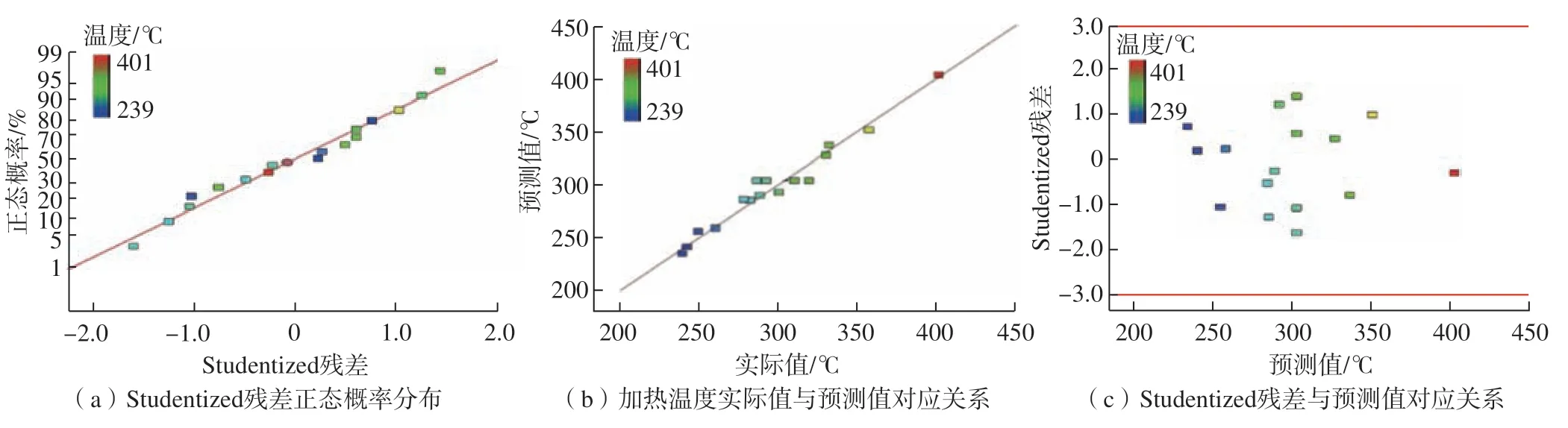
图4 模型适合性验证结果Fig.4 Model suitability verification results

3.3 拟合结果分析

3.3.1 单因素分析

从二次方程模型的拟合结果可以得到电压、脉宽和热源移动速度对加热温度的影响规律，如图5所示。可以看出，加热温度随着电压的增加而升高，随着脉宽和热源移动速度的增加而降低，这与第2节单因素试验的结果一致。同时，从增长的趋势也可以看到，脉宽对加热温度的影响较大，速度次之，电压最小，该规律也与拟合方程的分析结果一致。

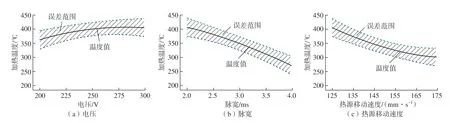
图5 电压、脉宽和热源移动速度对加热温度的影响规律Fig.5 Influencing of voltage, pulse width and heat source speed on heating temperature

3.3.2 响应因子交互作用分析

如图6所示，根据Quadratic模型的拟合方程和方差分析，得到电压对加热温度的影响最小，而脉宽和热源移动速度的交互作用对加热温度的影响最大。因此，研究了电压分别为200 V、250 V和300 V时的脉宽和热源移动速度对加热温度的交互作用影响。可以看出，当脉宽和速度一定时，随着电压的增大，加热温度呈增大的趋势，该结论与单因素试验结果一致。当电压一定时，脉宽和热源移动速度对加热温度的交互影响规律为只有当脉宽和热源移动速度同时减小时，加热温度显著升高。通过单因素的分析可知，这是由于脉宽与脉冲氙灯的峰值功率呈反比例关系，当脉宽和速度都减小时，可以同时增加峰值功率和加热时间，从而使加热温度显著升高。此外，还分别研究了脉宽为2 ms时的电压和热源移动速度对加热温度的交互作用影响 （图7），以及热源移动速度为125 mm/s时的电压和脉宽对加热温度的交互作用影响 （图8）。可以看出，当脉宽一定时，随着电压的增大和热源移动速度的减小，加热温度呈上升的趋势；当速度一定时，增大电压减小脉宽可增大加热温度。

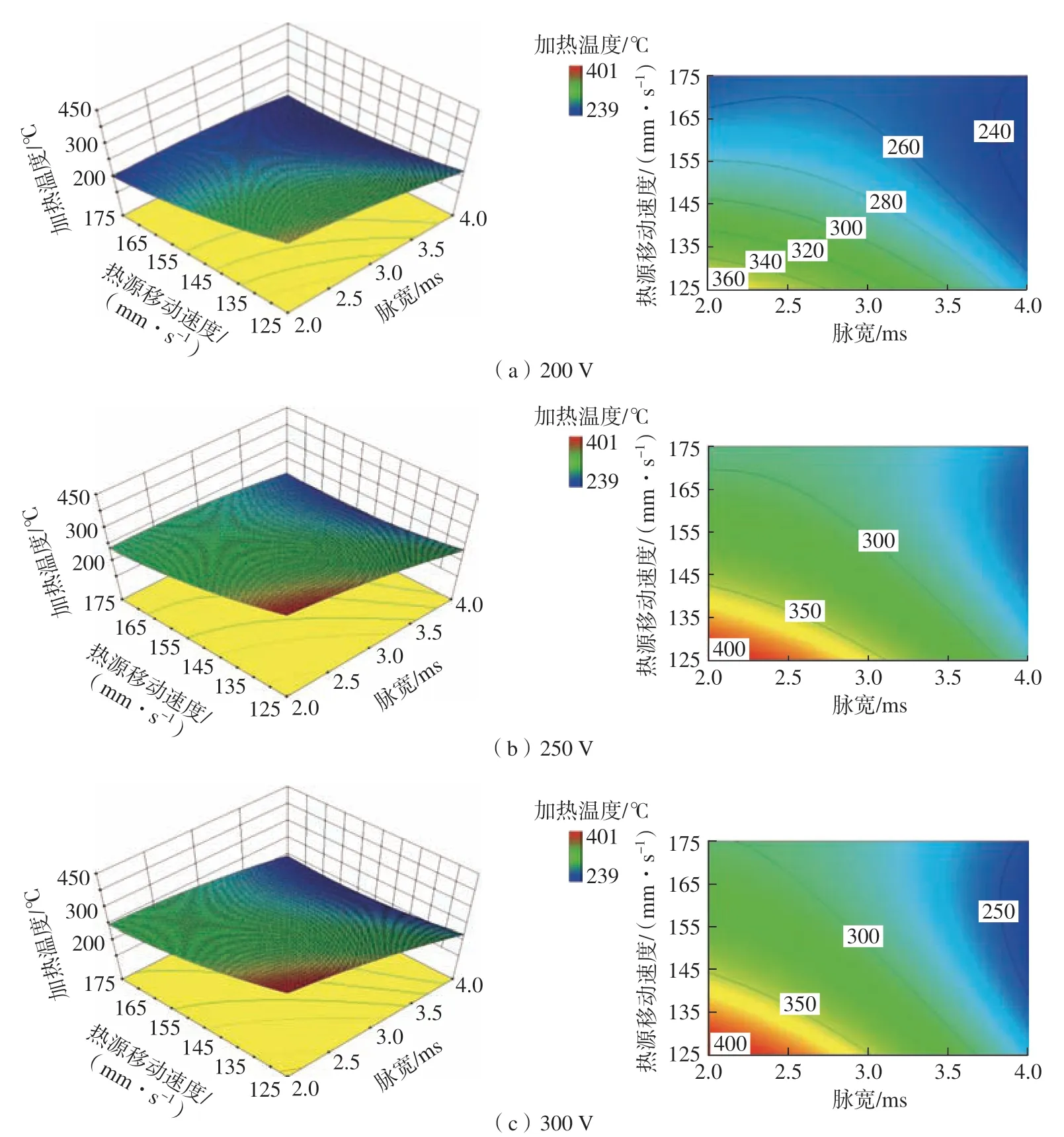
图6 不同电压下脉宽和热源移动速度对加热温度的交互作用等值线图Fig.6 Contour map of interaction between pulse width and moving speed of heat source on heating temperature under different voltages

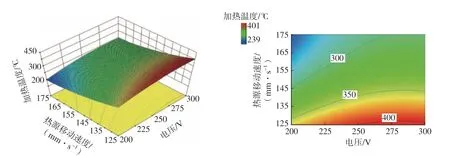
图7 脉宽2 ms时，电压和热源移动速度对加热温度的交互作用等值线图Fig.7 Contour map of interaction between voltage and moving speed of heat source on heating temperature at pulse width of 2 ms

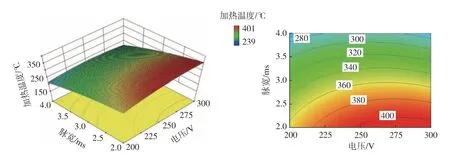
图8 热源移动速度125 mm/s时，电压和脉宽对加热温度的交互作用等值线图Fig.8 Contour map of interaction between voltage and pulse width on heating temperature at moving speed of heat source of 125 mm/s

3.3.3 CF/PEEK表面微观形貌

图9是未加热和最佳工艺参数下（加热温度381℃）的CF/PEEK–1预浸料的表面形貌。从图9（a）和（b）的宏观形貌可以看出，未经加热的预浸料表面平整光滑，而加热后的预浸料表面则出现褶皱变形。这主要是由于树脂和纤维的热膨胀系数不同，在加热后冷却的过程中产生的冷却收缩应变不同，导致褶皱的产生。从图9（c）和（d）微观形貌中可以看到，在加热温度为381℃时，部分区域纤维之间发生“分叉”现象，部分区域树脂较好地浸润于纤维之间，表明在该温度下树脂发生了充分的熔化，树脂的熔化使得预浸料内部纤维与树脂之间的残余应力得以消除[25–26]，故纤维发生“分叉”现象，同时树脂受热熔化流动，冷却后在部分区域浸润于纤维之间，故预浸料表面存在纤维“分叉”和树脂充分浸润的形貌。

图9 不同加热温度下的CF/PEEK的表面形貌Fig.9 Surface morphology of CF/PEEK at different heating temperatures

4 结论

（1）预浸料表面粗糙度对脉冲氙灯加热温度有较大的影响，表面粗糙度越小，加热温度越稳定；粗糙越大，加热温度波动越大。

（2）单因素试验分析得到，加热温度随电压的增加而升高，随脉宽和热源移动速度的增加而降低。二次方程模型拟合分析得到，电压、脉宽、热源移动速度对加热温度的影响程度为：脉宽>热源移动速度>电压；对加热温度的交互作用影响程度为：脉宽和热源移动速度>电压和脉宽>电压和热源移动速度。

（3）在工艺参数优化时，由于电压对加热温度的影响最小，可以先确定电压然后主要调整脉宽和热源移动速度，使加热温度满足相应复合材料的加热要求。对CF/PEEK–1预浸料加热的最优工艺参数为电压221 V，脉宽2 ms，热源移动速度125 mm/s，脉冲频率 60 Hz，灯口与预浸料之间的距离10 mm。此时，加热温度为381 ℃，树脂能够充分熔化，较好浸润于纤维之间。

（4）本文首次验证了脉冲氙灯可用于加热高性能热塑性复合材料，后续工作将重点研究脉冲氙灯辅助加热自动铺丝成型高性能热塑性复合材料构件的工艺优化，以及构件的力学性能研究。

致谢

感谢贺利氏 （沈阳）特种光源有限公司提供的脉冲氙灯加热设备。