基于可控K-means算法的任务均衡多旅行商问题求解
2022-08-25金明
金明
中国电子科技集团公司第二十八研究所 江苏 南京 210007
引言
m个旅行商从中心城市出发,遍历n个城市,每一个城市被且只被一个旅行商访问一次,最终返回中心城市,求解总路程最小的划分及遍历顺序,这是经典的多旅行商问题(mTSP)。当m=1时,该问题退化为单旅行商问题(TSP)。现实中很多问题可以简化为mTSP问题,比如无人机搜索覆盖、物资配送、不合格品控制等[1],因此该问题的求解具有重要意义,但mTSP是一个典型的NP难问题,精确计算方法具有指数级复杂度,只能用于求解小规模问题。mTSP问题一般包含两个优化目标,总路程最小及任务分配均衡,这两个目标并不是一致的,一般无法使这两个目标同时达到最优,通常任务均衡多旅行商问题求解更具现实意义[3-4]。
在求解mTSP问题时可以通过聚类提升算法性能[5],常用的聚类算法包括K-means算法、高斯混合聚类算法、密度聚类算法、层次聚类算法[6]。通过K-means聚类实现子集划分[7],聚类能够把距离相近的点划分成一个子集,各个子集之间互不交叉,仿真实验表明该方法能够获取更短的总路径,但文献中并未考虑任务均衡实现方法。K-means聚类的结果与数据分布密切相关,因此无法确保聚类结果的均衡性,本文在K-means聚类的基础上,基于簇中心距离最近原则,实现了可控K-means聚类,可用于任务均衡mTSP问题求解。
1 数学建模

于是任务均衡mTSp优化目标函数可以描述为:

其中:

表示第k个旅行商机动总距离,约束条件为[3]:

如果需要实现路线最短,只需把优化目标函数从式(3)改为:
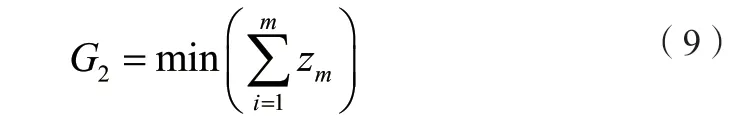
如果同时考虑两个因素的影响可以把优化目标函数修改为:

我们把mTSP分解为两个问题,一是如何把n个城市划分为m个不相交的子集,二是对每一个子集如何求解TSP,单个TSP可用经典的启发式算法求解。划分后的m个子集需满足式(11)。

2 可控K-means聚类算法
2.1 初始划分
假设要求的聚类中各个簇的元素数量为ni,并满足:
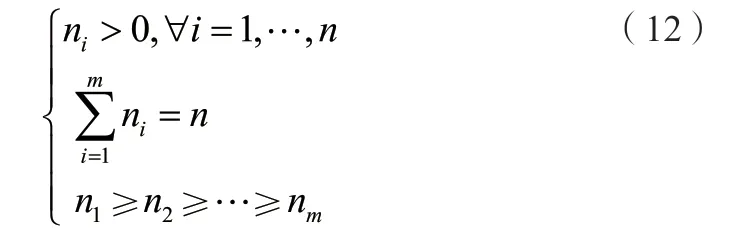

2.2 冲突消解
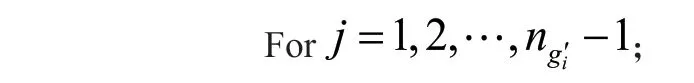
3 任务均衡算法
3.1 算法初始化
3.2 快速迭代
最后,使用TSP算法获取m个最小距离,计算并比较值,直到不再变大。
3.3 精细化搜索
然后,使用可控K-means聚类,获得指定元素数量的划分。之后,使用TSP算法获取m个最小距离,并计算值。
最后,如果 值比前一次迭代的值大,则继续迭代,否则返回前一次迭代结果,并结束迭代。
4 算法推广及应用
4.1 起点各异mTSP
对于m个旅行商起始城市各异问题,可以根据距离最近原则,把m个城市的聚类簇划分给m个旅行商,假设第i个旅行商的起始点设为,构建距离矩阵,矩阵中的元素表示第i个旅行商从城市出发到城市聚类簇中最短的距离,迭代取矩阵中的元素最小值,从而确定该旅行商和城市聚类簇之间的关系,然后删除矩阵最小值对应的行和列,如此重复,直到确定所有旅行商和聚类簇之间的对应关系。
4.2 多人巡检问题
我们还可以把多旅行商问题进行进一步推广成多人巡检问题,m个巡检人员需访问n个站点,每个站点除了站点间机动需要时间,站点巡检也需要时间,此时优化目标从距离均衡变为时间均衡。假设每一个旅行商的机动速度一致,都为,且每一个点位都需要一定的巡检时间,第i个点位的巡检时间设为,此时需要把任务分配给m个巡检人员,需要使各个巡检人员任务完成时间相对均衡。此时只需把算法中的的替换为即可,定义如下。
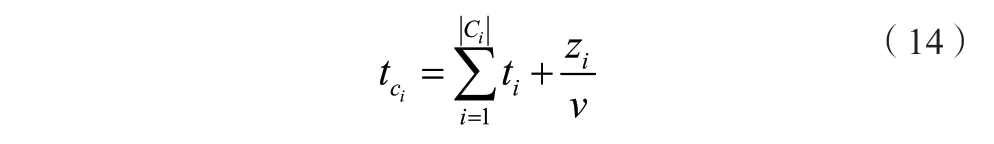
5 结束语
多旅行商问题总路程最小、任务分配均衡的两个优化目标彼此相关,但又不完全一致,本文通过K-means聚类,把距离相近的城市划为一类,可有效减少机动距离。同时针对常规聚类算法簇内元素数量不可控的问题,提出了可控K-means聚类算法。该算法基于簇中心距离最近原则进行聚类,通过消解冲突方法,获得指定元素数量的簇划分。该算法可用于任务均衡mTSP及其推广问题的求解。

