基于PSO的无刷直流电机PI参数自整定仿真研究

樊星男

(太原学院 机电与车辆工程系，山西 太原 030032)

0 引言

无刷直流电机(brushless direct current motor，BLDCM)以其优良的机电特性被广泛应用于精细控制领域，而PI控制一直都是BLDCM重要的控制方法。对于PI参数的整定，大多需要依赖技术人员的经验进行调整，对技术人员的经验依赖性较强，常常难以满足控制要求。

群粒子优化算法(particle swarm optimization，PSO)是一种群智能优化算法，具有全局最优搜索能力，它只信赖于适应度函数，不需要了解对象的全部信息，这样即使在对象模型不确定的情况下，仍然可以根据对象的输出情况对PI参数进行优化。常用的适应度函数主要是基于误差的泛函数积分，包括IAE、ITAE、ISTAE、ISE、ITSE、ISTSE，但是在使用这些适应度函数进行PI参数整定时得到的系统控制效果是不一样的，它们各自侧重于对系统某个阶段或某种状态有较好的控制效果，而很难对系统的整个动静态过程有一个全面的考量。为此，本文提出了一种以系统动态性能指标为参考依据的适应度函数，通过群粒子优化算法对无刷直流电机调速系统中的PI 参数进行自动整定。仿真结果表明，通过该适应度函数寻优获得的PI参数具有更优越的控制特性。

1 BLDCM的数学建模与仿真系统设计

1.1 BLDCM在PI控制下的性能分析

无刷直流电机在PI控制下，其系统框图如图1所示。

图1 无刷直流电机PI控制系统框图Fig.1 The block diagram of PI control system for brushless DC motor

图1中，GPI(s)表示PI控制器的传递函数，Gd(s)表示电机的传递函数，R(s)表示系统输入，E(s)表示系统误差。

PI控制器的传递函数表示见公式(1)。

(1)

式中：KP表示比例系数；KI表示积分系数。

无刷直流电机在忽略换相时电流变化的暂态过程情况下，其A、B、C三相电流可近似认为是两两导通，此时其传递函数表示见公式(2)。

(2)

式中：R为电机线等效电阻；L为线等效电感；KE为反电势系数；KT为电机转矩系数；J为转动惯量；B为粘性阻尼系数。

系统误差表示见公式(3)。

(3)

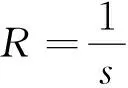
(4)

由公式(4)可以看到，无刷直流电机在PI控制下，其稳态误差为0。因此，对PI参数的调节主要针对的是对电机动态性能的调节。

1.2 BLDCM PI控制系统仿真模型设计

如图2所示，无刷直流电机调速系统采用单闭环控制，采样时间为5 μs，主要包括电机本体、可控直流电源、PI控制器、全桥逆变器和逆变器控制器[1-2]。

当系统启动后，系统预设转速与电机实际转速的差值作为PI控制器的输入量，PI控制器根据输入量和自身的PI参数经计算后产生控制信号，控制可控直流电源的输出电压大小，可控直流电源的输出电压是全桥逆变器的输入电压，而全桥逆变器根据逆变器控制器产生的门控信号将直流电源的输出电压分配给电机定子上的三相绕组，使得三相绕组两两相通，每相导通120°电度角，每60°电度角进行一次换向，从而使电机产生持续的转矩[3-4]。

图2 BLDCM PI控制系统仿真图Fig.2 The simulation diagram of PI control system for BLDCM

在仿真模型中，电机本体采用的是Simulink中的PMSM电机模型梯形波模式；全桥逆变器主要由6个场效应晶体管组成，如图3所示。逆变器控制器采用MATLAB嵌入函数设计完成，通过读取电机上的霍尔信号生成逆变器控制信号。控制器的控制逻辑如表1所示，如当逆变器控制器检测到电机ABC三相的霍尔信号为001时，控制器发出的6个门控信号为000110，表示图3所示逆变器的场效应管Q4和Q5导通，其他场效应管截止。

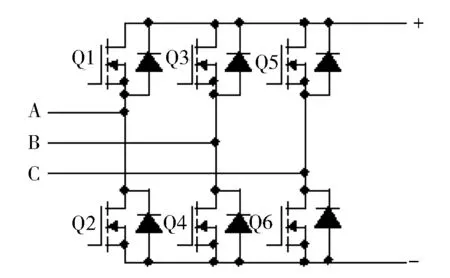
图3 逆变器组成图Fig.3 The composition diagram of the inverter

表1 逆变器控制器控制逻辑Tab.1 The Control logic of the inverter controller

2 基于群粒子优化的PI自整定

2.1 群粒子算法原理

粒子群优化算法(PSO)[5-6]是一种仿生算法，源于对鸟群捕食的行为研究，其基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。群粒子算法表现形式简单，具有较好的全局搜索能力，目前已经被广泛应用于多参数问题的最优解优化问题[7]。

PSO算法可以用公式(5)所示的数学公式进行表示。

(5)

式中：i表示第i个粒子；n表示迭代次数；ΔUi(n+1)表示粒子的移动距离；Ui(n)表示粒子的当前位置；ω为惯性系数，范围[0,1]；c1和c2为加速因子，表示粒子移动的速度,范围[0,2]；r1和r2为[0,1]区间的随机数；Uimax表示当前粒子的历史最佳位置；Ugmax表示所有粒子中最佳粒子的位置。

使用PSO算法进行自动寻优，可以描述为粒子个体不断逼近食物源的过程，这个过程用数学描述就是一个计算适应度函数极小值的过程，所以在选取或者设计适应度函数时，该函数必须是具备极小值的[8]。

2.2 基于误差的泛函积分适应度函数

基于误差的泛函积分适应度函数是在解决自动寻优问题过程中使用非常广泛的一类适应度函数，它包括IAE、ITAE、ISTAE、ISE、ITSE和ISTSE共6个函数[9]，其表示方法如表2所示。

表2 误差泛函积分适应度函数Tab.2 The fitness functions of error functional integral

表2中e(t)表示t时刻系统的误差。从表2可以看出，误差泛函积分适应度函数主要是通过判断误差不同积分方式下数值的大小来评判系统的优劣程度。在这种评判标准下，很容易出现一种问题，那就是系统可能会出现多次短时快速的波动，而由于时间短，其误差积分值并不高。但是，这样的系统并不平稳，有可能会导致出现整个设备的共振现象，对设备危害较大。

2.3 适应度函数的构造

由前文1.1知道，使用PI控制的无刷直流电机系统对于阶跃响应的稳态误差为零，因此在设计适应度函数时只需要考虑系统的动态性能。为此本文以系统动态性能指标为直接评价参数，提出了一种新的适应度函数，其数学表示见公式(6)。

Y=K1F+K2S

(6)

式中：F(Fast)用来描述系统的快速性；S(Stability)用来描述系统的相对稳定性；K1、K2分别表示F、S的权重。

系统动态性能中的快速性和相对稳定性往往是相悖的。通常系统的快速性越强，产生的超调量和振荡次数就越大，也就是相对稳定性越差；而系统的相对稳定性越好，系统的快速性就会越差。所以电机的控制中总是需要根据实际情况在快速性和稳定性这二者之间进行权衡，不断修改控制参数从而达到一个相对最佳的控制策略。通过修改K1、K2可以改变F、S在整个公式中的权重，从而修改自动寻优的侧重方向，比如提高K1的值可以让寻优向快速性方面倾斜。这样就可以在寻优过程中更加方便快速地获得理想PI参数，同时也将PI整定过程变得更加简单有效。

F的数学表示见公式(7)。

F=tr+ts

(7)

式中：tr表示系统的上升时间；ts表示系统的调节时间。从公式(7)可以看出，F值越小，电机转速上升得越快。

S的数学表示见公式(8)。

(8)

式中：Mi表示系统在进入稳态之前的极值；N表示极值个数；I为系统运行的预设转速。从公式(8)可以看出，S值越小，电机在进入稳态前的波动幅度和波动次数越小，电机运行越平稳。

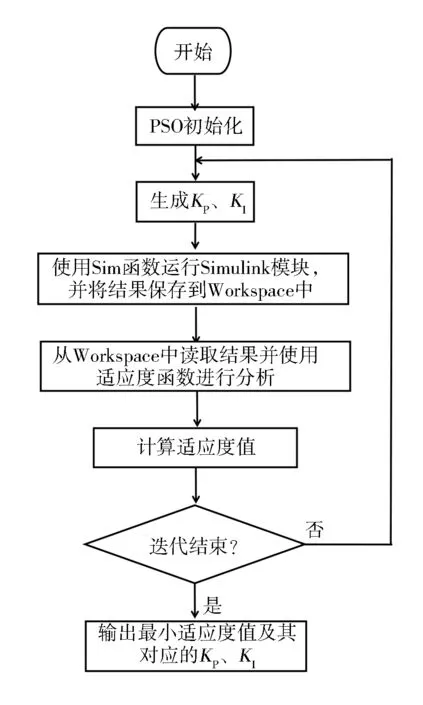
图4 基于PSO算法的PI整定流程图Fig.4 The flow chart of PI tuning based on PSO algorithm

3 仿真试验研究

3.1 仿真系统设计

基于群粒子优化算法的PI整定在BLDCM调速中的应用仿真系统采用了MATLAB函数与Simulink模型相结合的仿真方法，其中MATLAB函数主要进行PSO算法的计算，Simulink模块主要进行BLDCM调速系统仿真。仿真流程如图4 所示，BLDCM调速系统运行完成后，将采样到的数据保存到MATLAB的Workspace中，然后PSO算法读取这些数据进行分析并产生新的PI参数，如此反复，直到获得最优PI参数。

3.2 参数设置

设置Simulink模块仿真时长为0.2 s，目标转速为3 000 r/min；Simulink模块中的电机模型选用的是MATLAB软件中自带的power_brushless DC motor仿真实例中的电机模型，该电机模型的主要参数如下：

1)电机线电阻r=5.7 Ω；2)电机线电感l=0.017 H；3)转动惯量J=0.000 8 kg·m2；4)粘性阻尼系数B=0.001 N·m·s。

在该实例中，MATLAB软件给出的PI参数为KP=0.013,KI=16.61。

设置群粒子算法的最大迭代数为100，粒子种群数量20，KP和KI的取值范围均为[0,100]；分别设置适应度函数中的权重因子K1=K2=1和K1=5,K2=1进行两次寻优。

3.3 仿真结果及分析

分别使用基于误差的泛函积分的6个适应度函数和本文适应度函数，使用PSO算法进行寻优计算。考虑到寻优算法可能存在局部最优解的问题，分别对以上适应度函数进行多次独立的寻优计算并选取最优解作为最终寻优结果，如表3所示。

表3中，本文(1)适应度函数的权重因子K1=K2=1，本文(2)的适应度函数的权重因子K1=5,K2=1。

表3 各适应度函数最优结果Tab.3 The optimal results of each fitness function

从表3可以看出，使用本文适应度函数寻优得到最优解分别为KP=0.006 0,KI=12.058 0和KP=0.009 0,KI=19.267 4，这两个结果最接近于MATLAB软件给出的PI值，这也验证了本文适应度函数的可行性。

使用表3中不同适应度函数寻优得到的最优参数仿真电机调速过程，波形见图5和图6。

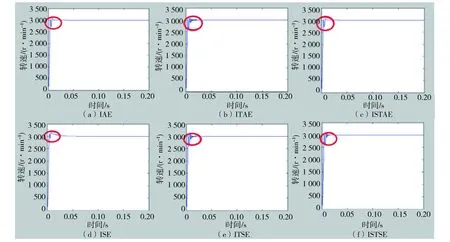
图5 误差泛函积分适应度函数最优结果Fig.5 The optimal results of error functional integral fitness functions

图6 本文适应度函数最优结果Fig.6 The best optimalresults of fitness function in this paper

从图5可以看出，使用误差积分泛函适应度函数得到的PI控制器在调节电机转速时电机的快速性很好，但是相对稳定性较差，在调速过程中出现了多次快速振动。

从图6可以看出，使用本文适应度函数寻优得到的PI控制器在调节电机转速的过程中快速性稍差，但是相对稳定性更好，整个动态过程更加平滑稳定。

图6中实线为权重因子K1=K2=1对应的曲线，虚线为权重因子K1=5,K2=1对应的曲线，比较这两条曲线可以看出，通过增大适应度函数中F(Fast)的权重因子所得到的最优PI参数可以有效提高系统的快速性。

在0.1 s处向电机施加F=3 N·m的负载，仿真波形如图7所示。从图中可以看出，施加负载后系统能够迅速地进行调节并恢复到预设转速，具有良好的抗干扰性。

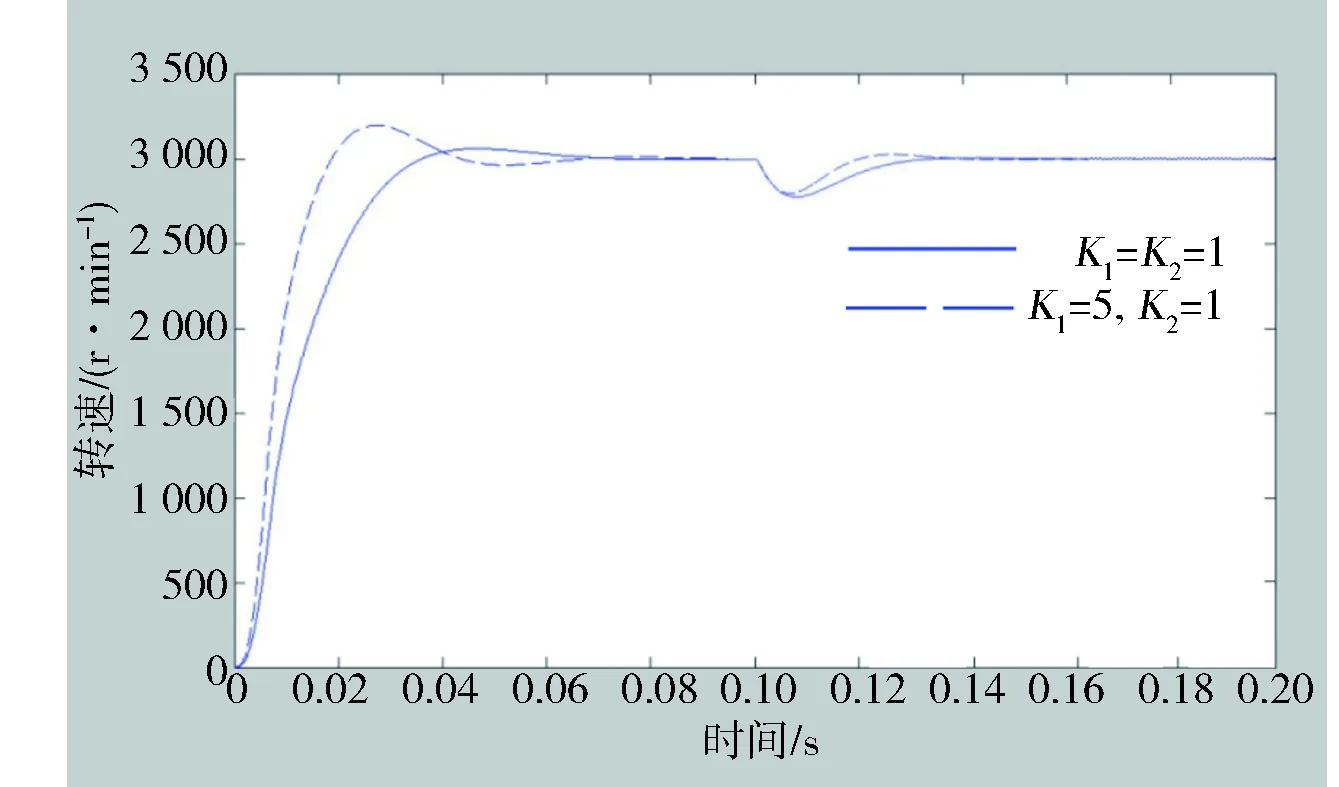
图7 本文适应度函数施加负载后仿真波形图Fig.7 The optimalresults of fitness function in this paper after loading

4 结论

通过以上仿真比较和分析可以看出，本文提出的新的适应度函数，在无刷直流电机调速系统PI参数整定方面的应用是可行的，使用该适应度函数所得到的PI参数最接近于MATLAB给出的最优PI参数，其整体控制效果也明显优于误差积分泛函适应度函数，并且在调节系统快速性、相对稳定性和稳态误差方面具有更加灵活的可操作性。