网络化运营地铁区间中断的影响传播规律

刘 悦，冯旭杰，连训萍，何 祥，刘书浩，胡 昊

（1.交通运输部科学研究院，北京 100029；2.城市轨道交通运营安全管理技术及装备交通运输行业研发中心，北京 100029；3.福建省运输事业发展中心，福建 福州 350001）

0 引言

随着地铁线网的形成，单一故障点引起的客流堆积会通过换乘车站等节点进行传播，从而对整个线网造成影响。据中国城市轨道交通协会统计，2020 年共发生5min 及以上延误事件1 023件[1]，其中发生30min 以上的连续中断行车超过20 起，对地铁运营安全和服务质量造成了较大影响。由于对客流规律掌握不足，导致运营单位制定的区间中断应急处置措施的针对性有待提升，影响了运营秩序的恢复效率。因此，开展网络化运营地铁区间中断的影响传播规律研究非常必要。

目前对于异常事件下地铁客流影响的研究主要集中在突发大客流的传播规律以及应对方面。在突发大客流的传播规律研究方面，元胞自动机模型（Cellular Automata,CA）是使用较为广泛的分析模型，如：张琦等[2]、李曼等[3]、刘纹滔[4]、蒋阳升等[5]构建了基于CA 的线网突发客流消散仿真模型；史宇峰等[6]则聚焦站台，构建了基于CA 的站台大客流疏散模型。此外SIR（Susceptible Infected Recovered）和SIRS（Susceptible Infected Recovered Susceptible）传染病模型也被引入，如李凌燕[7]提出了带有直接免疫的SIRS 大客流路网传播模型，李朴[8]、牛龙飞[9]、曹志超[10]以及郑雪梅[11]等结合复杂网络理论、系统动力学理论等，建立了基于SIR 的城市轨道交通拥堵传播模型。在轨道交通故障条件下的应急处置方面，国内外学者对加开列车、应急公交接驳等方面开展了研究，如：白荣[12]、Cadarso 等[13]、Binder 等[14]、Yin 等[15]等对加开列车的数量和时机进行了分析；Gu 等[16]、Chen 等[17]对应急公交接驳的路线衔接和时刻表优化等方面开展了研究。学者们均认识到故障影响传播规律研究的重要性，但是大多数研究停留在理论分析和仿真模拟层面，使用实际发生的地铁故障条件下的数据进行验证的研究较少，对实际客流管控的指导性不足。因此，通过实际案例对网络化运营地铁区间中断的影响传播规律进行剖析非常重要。

本文对2020年国内某地铁区间中断故障真实数据进行了分析，通过出行时间、进站量以及出站量三项指标研究了区间中断故障影响的发生、传播和消散的动态过程，总结出区间中断故障对地铁线网客流的影响规律，并对传播规律进行了一般性归纳总结，据此为地铁突发事件下应急处置的范围和应急处置措施策略的选取提出建议，以提升地铁线网韧性水平。

1 地铁区间中断影响传播规律实例分析

为剖析区间中断故障对地铁客流时空分布的影响，本文通过对比某城市正常运营情况下与发生区间中断情况下的乘客进出站刷卡数据，分析在同样的线网条件和基本相同的出行需求下，故障对地铁线网乘客出行的影响。

本文中相关参数的定义如表1所示。

表1 参数定义

正常运营条件下单位时间内车站i所在线路j的进站量为：

与正常运营情况下相比，单位时间内线路j的进站量减少量为：

式（2）中：为区间中断情况下相同时间段内线路j的进站量。

正常运营情况下单位时间内车站i所在线路j的出站量为：

与正常运营相比，单位时间内线路j的进站量减少量为：

式（4）中：为故障情况下相同时间段内线路j的出站量。

单位时间内以车站i为起点出行的乘客的出行总时间可表示为：

式（5）中：i′为乘客出站车站，i′可以和i同属一条线路，也可以不属于一条线路。

从车站i进站乘客平均出行时间可表示为：

由于故障导致的车站i出行乘客平均时间延长可表示为：

式（7）中：为故障情况下相同时间段内选择车站i进站乘车的乘客的出行总时间，为故障条件下相同时间段内线路j上车站i单位时间内的进站量。

路线j的平均出行时间可以采用下式计算：

选择线路j出行乘客的平均出行时间延长可表示为：

某城市拥有地铁线路3 条，分别为1 号线、2号线及3 号线，相互关联成为网格状，总里程89.6km，开通运营车站共计80座，初步形成了网络化运营格局。某日，地铁3 号线某一列车发生紧急制动无法缓解，导致304—305站上行区间出现中断，如图1 所示。当日6：20 开始，该列车偏离计划运行图；7：15 时，所有列车均未按计划运行；8：00 以后，列车运行逐渐恢复；直到9：40，所有列车按原计划的发车间隔和停站时间运行。本次区间中断故障期间，于7：01 加开了一列起始站为313 站的上行列车。本次列车故障的影响时段为当日6：20—9：40，覆盖了整个早高峰时期，对列车运行和乘客出行造成了较大的影响。

图1 304—305站上行区间列车故障

1.1 出行时间

由于故障发生，选择地铁出行的乘客均受到不同程度的影响。为进一步明晰故障影响趋势，本文选择故障发生时刻6：20、线路所有列车偏离运行图时刻7：15、列车运行逐渐恢复时刻8：00以及运行全面恢复时刻9：40为关键时间节点，将故障时间段分为6：20—7：15,7：15—8：00 以及8：00—9：40，分别对不同时间段内乘客出行时间进行分析。

首先，区间中断造成故障线路（以下简称本线路）乘客出行时间延长，特别是对运行中断车站及沿中断运行方向相邻车站造成的影响更为显著。如图2 所示，以地铁3 号线为起点站出行的乘客的出行时间均有所增加，6：20—7：15期间为6.3min。其中从301～309 站出行的乘客时间增幅为6.9min，高于其他车站。由于330～333 站在6:20—9:40 期间进站量极小，乘客出行随机性较大，其出行时间不具有统计学意义，图2中未予以显示。

图2 地铁3号线在故障与正常情况下乘客平均出行时间差值

其次，区间中断会对换乘线路造成影响，对不同换乘线路影响不同，且对换乘线路的影响小于本线路；同一线路不同车站受影响程度不同。如图3 所示，对于1 号线，109 站及周边车站、117 站及周边车站受到故障的影响高于本线路的其他车站；如图4 所示，对于2 号线，其起始车站203 站、换乘车站210 站（即313 站）和216 站（即104站）及其周边车站受到故障的影响高于本线路的其他车站，在故障情况下乘客平均出行时间延长幅度高于其他车站。但相对于1 号线各车站而言，2 号线各车站受到的影响均较小。由于114 及122、123 车站在6：20—9：40 期间进站量极小，乘客出行随机性较大，其出行时间不具有统计学意义，图3中未予以显示。

图3 地铁1号线在故障与正常情况下乘客平均出行时间差值

图4 地铁2号线在故障与正常情况下乘客平均出行时间差值

最后，故障影响在线网中的传播需要一定的时间，故障首先对本线路造成影响，而后对换乘出行的乘客造成影响。如图5 所示，6：20—7：15，故障首先对3 号线造成冲击，在7：00 加开了上行区间列车后故障对乘客的出行时间影响有所降低；对2 号线的影响始于6：35—6：40，6：50—7：00 乘客出行时间增加最为显著，平均出行时间增加6.8min；对1 号线的影响时段要晚于3 号线和2号线，始于6：45—6：50，在故障对3 号线和2 号线的影响有所降低时仍保持上升趋势，7：00—7：15 期间以1 号线为起点站出行的乘客平均出行时间增加7.5min。

图5 6：20—7：15各条线路在故障与正常情况下乘客平均出行时间差值

1.2 进站量

比较地铁线网各条线路在区间中断条件下和正常运营条件下早高峰时期的进站量变化，具体如下。

首先，故障当日和正常运营条件下的整体客流规律基本相同，但故障当日高峰时段具有时长缩短、延迟到来、提前结束的特点。如图6～图8所示，故障当日和正常运营条件下各条线路进站量曲线在早高峰均呈现中间高两边低的“凸形”，但故障当日高峰持续时间缩短。其中2 号线高峰时段出现时间延迟约5min，约提前15min 结束；1 号线高峰时段出现时间延迟约15min，约提前25min结束。

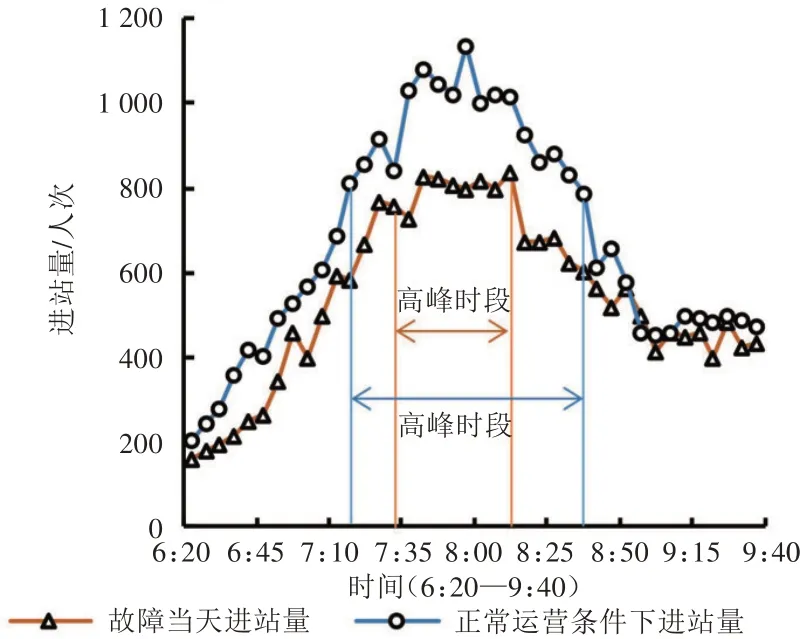
图6 正常运营与故障情况下地铁1号线进站量

图7 正常运营与故障情况下地铁2号线进站量

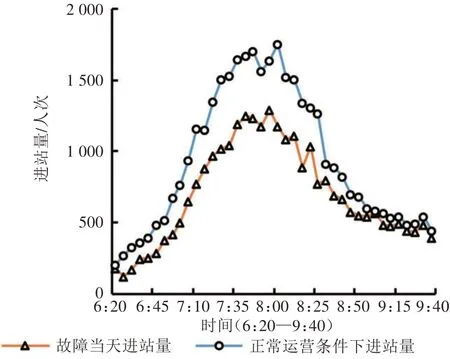
图8 正常运营与故障情况下地铁3号线进站量

其次，受故障影响，地铁1 号线、2 号线和3号线的进站量与正常情况下相比均有不同程度的降低，进站量差值如图9所示。6：20—8：50期间，3 号线进站量受到的影响最大，降低幅度明显高于1 号线和2 号线。在此时间段内，3 号线进站量累计减少28.3%（ΔO3为9 206 人次），2 号线累计减少18.7%（ΔO2为8 146 人次），1 号线累计减少22.2%（ΔO1为5 054 人次）。8：50—9：40 期间，随着列车运行的逐渐恢复，1 号线和3 号线的进站量基本恢复到正常运营水平，而2 号线进站量超过了正常运营水平，在实施应急处置措施时应予以注意。

图9 正常运营与故障情况下各线路进站量差值

再次，运营恢复阶段进站量会逐步回升，甚至超过同期。从乘客出行意愿来看，虽然故障当日9:40 后所有列车才按原计划的发车间隔和停站时间运行，如图6～图8所示，但9：00时故障对乘客出行意愿的影响就已基本消散，9：00 之后的进站量甚至可能会有所提升，运营单位应予以关注。

最后，从各条线路车站的进站量变化情况来看，故障对故障发生区段及相邻车站，换乘车站及周边车站的进站量有不同程度的影响。如图10所示，对于3 号线车站，6：20 时故障发生区段车站的进站量最先发生明显减少，随后相邻车站进站量出现了不同程度的减少；对于1 号线和2 号线，线路换乘车站进站量及周边车站较其他车站减少量更为显著；对于2 号线，在8：50—9：40 时间段内，有87.5%的车站进站量恢复到正常运营情况或有所增长；对于1 号线，在9：15—9：40 时间段内，有39.1%的车站进站量恢复到正常运营情况或有所增长。

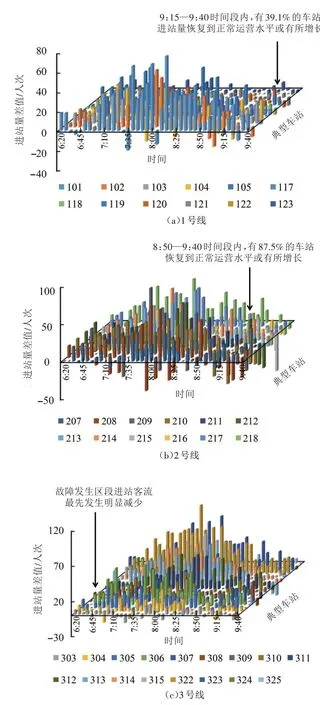
图10 正常运营与故障情况下典型车站进站量差值（6:20—9:40）

1.3 出站量

比较地铁线网各条线路中断条件下和正常运营条件下早高峰时期的出站量空间分布，具体如下。

首先，故障当日和正常运营条件下的整体客流规律基本相同，但出现明显削峰现象。如图11～图13 所示，故障当日出站量随着时间的推移缓慢增加，但是随后没有与正常运营情况一样继续上升进入峰值，而是进入一段较长时间的持平期。因为发生中断后，进站乘客不能在短时间内登上列车，导致候车时间变长，出站峰值延迟到来。受故障影响，线网各线路的出站量较正常运营情况下均有不同程度的降低，出站量差值如图14所示。在6：20—9：00时间段内，3号线出站量受到的影响更大，降低幅度明显高于1 号线和2号线，在此时间段内中，3 号线出站量累计减少29.0%（ΔD3为9 014 人次），2 号线累计减少20.8%（ΔD2为8 568 人次），1 号线累计减少24.0%（ΔD1为5 052 人次）。对于峰值而言，3 号线出站量减少33.1%，1 号线减少26.1%，2 号线减少23.7%。9：00—9：40 时间段内，随着列车逐渐恢复运行，各条线路的出站量基本恢复到正常水平。

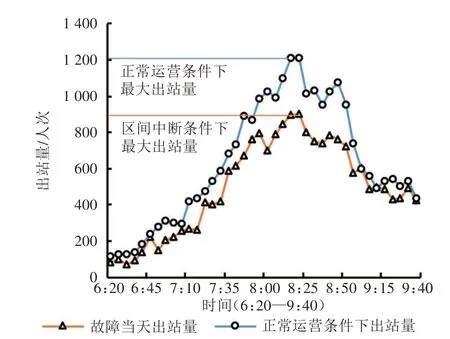
图11 正常运营与故障情况下地铁1号线出站量

图12 正常运营与故障情况下地铁2号线出站量

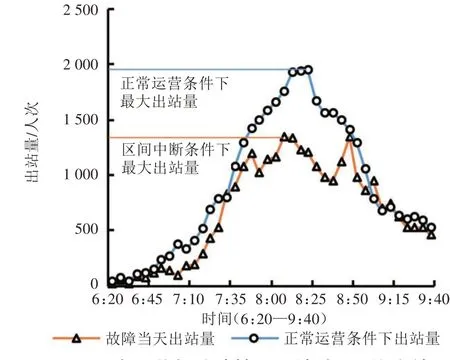
图13 正常运营与故障情况下地铁3号线出站量

图14 正常运营与故障情况下各线路出站量差值

其次，从各条线路车站的出站量变化情况来看，故障对故障发生区段及相邻车站，换乘车站及周边车站的出站量有不同程度的影响。如图15所示，对于3 号线车站，6：25 时故障发生区段及相邻的各个车站的出站量最先出现了较为明显的减少；对于1 号线和2 号线车站，换乘车站及其周边车站出站量较其他车站减少量更为显著；对于2 号线，在9：10—9：40 时间段内，有62.5%的车站出站量恢复到正常运营水平或有所增长；对于1 号线，在9：25—9：40 时间段内，有52.1%的车站出站量恢复到正常运营水平或有所增长。

图15 正常运营与故障情况下典型车站出站量差值（6:20—9:40）

1.4 区间中断传播时空推演分析

随着区间中断的影响范围不断扩大，全线网均受到了一定的影响，故障影响按照“点—线—面”进行传播。由1.1～1.3节可知，区间中断对本线路以及形成换乘关系的线路造成的影响在时空上存在差异。如图16所示，依照时间顺序对故障的传播推演如下。

图16 故障传播范围

首先，区间中断发生于6:20，即刻对3 号线的运营和乘客出行造成影响。如图8 和图13 所示，相对于1号线和2号线，区间中断对3号线的影响更为显著，从空间维度来看，对全线车站均造成影响，尤其是对中断区间及相邻各个车站影响更为显著；从时间维度来看，乘客出行时间的延长幅度明显高于1 号线和2 号线，分别达到42.8%及76.5%。

随后，6:35 即故障发生15min 后，从空间维度来看，故障影响由换乘车站313 传播至2 号线，对乘坐2 号线出行的乘客造成影响。从时间维度看，如图7 和图12 所示，6：35—7：00 期间，2 号线的进站量较同期有明显变化，减少了31.2%，而在此期间出行的乘客的出行时间显著增加，平均出行时间增加6.8min；由于3 号线加开了列车，对乘客出行的影响有所缓解，7：00—7：40 期间2 号线进站量减少了18.3%。故障对2 号线的进出站量影响于8：50—9：40期间基本缓解，8：50起对乘客进站的影响显著降低，9:10 起出站量逐步恢复到正常运营水平，8：00—9：40 出行的乘客的平均出行时间虽仍有延长，但小于6：20—8：00出行的乘客。

最后，6：45 即故障发生25min 后，从空间维度来看，故障影响经由换乘车站101 传播至1 号线，对乘坐1 号线出行的乘客造成影响，至此本次故障影响已传播至线网全部线路。从时间维度看，如图6 和图11 所示，6：45—7：10 期间，乘客进站量减少26.6%；7：10—7：40 期间，受加开列车影响，乘客出行时间延长有所减少，进站量减少幅度下降，进站量减少约20.4%；故障对1 号线的影响于9：25 起基本缓解，9：25—9：40 期间，有半数以上的车站的出站量恢复到正常运营条件下水平。与2号线相比，1号线受到故障的影响较晚，但影响幅度较大。

2 地铁区间中断影响传播规律理论分析

基于本文第一章节某城市地铁区间故障实例分析，本节重点对一般情况进行理论分析。对于故障线路，本应乘坐故障列车及后续列车出行的乘客无法按照原计划出行，在短时间内聚集在站台和站厅，对地铁运营造成较大影响。特别是在早晚高峰时期，出行客流量较大，行车密度高，一旦发生区间中断就会在较短的时间内造成多列列车晚点，线路通行能力下降，不仅对发生故障的区段，而且对于故障线路其他车站的乘客出行亦会造成影响。

地铁形成线网后，故障的影响不仅仅局限于故障线路，也会通过换乘客流的聚集和疏散对其他线路造成影响，如图17 所示。由于区间中断，换乘至故障线路的客流无法及时出行，从而造成了地铁区间中断的影响在地铁线网内传播。通过第一章节的实例分析，可以对出行时间、进站量以及出站量开展一般性理论分析。

图17 故障线网传播示意图

对于出行时间而言，对于i∈S∪R，由于区间中断，故障线路部分乘客滞留于车站内，延后导致增加，进而呈现出乘客出行时间延长的现象；对于i∈R，发生区间中断后本线路后续列车不能正常运行，随着时间推移，相邻车站及整条线路都会受到严重影响，会在区间故障发生后开始增加，但通过增开区间列车的方法可以有效降低；对于i∈X，需要换乘故障线路出行的乘客会显著增加，导致相应线路的Tˉj增加，此时，线网内中断线路影响的传播具体体现为全网车站乘客的平均出行时间增加。

对于进站量而言，当区间出现中断，乘客出行意愿降低，选择推迟出行或换乘其他交通方式的人数增加，Oj减少，故障线路高峰时段延迟到来、提前结束。由于部分乘客需要通过换乘乘坐故障线路，当区间中断后其出行意愿同样受到阻碍，导致换乘线路Oj同步减少。当列车恢复运行后，乘客会继续选择地铁出行，运营恢复阶段Oj会逐步回升，甚至超过同期。此时，线网内中断线路影响的传播具体体现为高峰时段时长缩短、延迟到来、提前结束，并且高峰进站客流量明显减少。

对于出站量而言，当区间出现中断，由于故障线路内乘客无法换乘到其他线路上，同时Oj减少，导致全网范围内Dj下降。对于i∈S∪R，由于需要在这些站下车的乘客无法在区间中断期间抵达目的地，所以会明显下降；对于i∈X，除需要换乘故障线路的乘客外，其他乘客可以正常抵达，但同样会出现下降。此时，线网内区间中断影响的传播具体体现为全网列车出站量出现削峰现象。

3 应对策略分析

区间中断发生后，运营单位需根据故障发生的位置和故障影响传播规律及时采取有针对性的处置措施，防止故障对正常运营造成重大冲击。

（1）对于故障线路，可视情况采取进站限流、加开列车和应急公交接驳等措施应对区间中断造成的影响。除中断区间，应重点关注中断区间周边车站、换乘车站及大客流车站，例如本案例中301～309 车站。为减缓客流涌入速度，应及时采取进站限流、关闭部分闸机等措施缓解站台和站厅的客流拥挤程度。同时考虑到区间中断后将有较长的时间无列车通过，此时应在及时处置区间中断故障的同时，在线路条件允许的情况下适时加开区间列车，可以有效缓解故障线路及换乘线路乘客的出行延误，如本次故障中自313 站开行上行列车。如区间故障难以在较短时间内处置完毕，有大客流聚集等情况出现时，应及时启动应急公交接驳疏散人群，直到受影响区段恢复安全运行条件，滞留乘客疏散完毕为止。

（2）对于换乘线路，可适时启动换乘客流疏导和列车跳停等方式应对区间中断传播影响。故障影响传播需要一定过程，在故障发生后需参考换乘车站距离中断区间的距离，及时启动应对措施，对换乘客流进行疏导，避免堆积在站厅和站台。此时对距离中断区间不同距离的换乘线路均应予以重视，如本案例中换乘线路1 号线和2 号线均受到3 号线区间中断的影响，虽然故障影响首先传播至2 号线，但对1 号线的影响更为显著。当车站客流已接近车站的容纳能力时，换乘线路应及时实施列车跳停，以降低运营风险，保证乘客的人身和财产安全。

（3）在区间中断处置完毕后，应及时关注本线路及换乘线路的客流进出站情况，可能在行车恢复后迎来超过正常运营条件下的进站量，如本案例中在9:00 后2 号线的部分车站进站量超过了正常运营情况，因此客流管控措施不宜过早解除。

4 结语

本文基于某城市发生的地铁区间中断实例，研究网络化运营地铁区间中断的影响传播规律。选取乘客出行时间、进站量以及出站量3个指标，对区间中断对不同线路、不同车站的影响的时域变化规律进行了分析。这3 个指标可以直接通过地铁进出站刷卡记录获取，客观反映网络化条件下区间中断的传播规律。结果表明，地铁网络化运营条件下，单线发生的区间中断会通过换乘车站对全线网造成影响；区间中断对本线路影响最为显著，特别是区间中断车站及沿中断运行方向相邻车站；故障同样对于形成换乘关系的其他线路造成影响，但影响程度较弱，并且影响的传播需要一定的时间；随着时间推移，故障对各条线路的影响逐渐增大，随着故障处置完毕和运行秩序的恢复，影响发生衰减直至消退；发生在高峰时刻前的区间中断会对客流高峰造成“削峰”现象，同时呈现高峰出现时间延迟、结束时间提前的特点。最后，对故障影响传播规律作了一般性理论分析，并提出了区间中断应对策略。

本文主要对乘客的出行数据进行了分析和总结，尚未基于此对客流消散仿真模型的有效性进行进一步探究。下一步，可结合车站乘客出行特征，基于实际发生的区间中断故障中乘客进出站刷卡数据，对基于CA 的突发客流消散仿真模型等相关研究中的关键参数进行辨识，给出参数选取的合理区间以及参数选取标准，提升建模的准确性。