基于IDWPSO-K-means聚类的网约车需求量时变特征分析

付文华，白 竹，张 蕾，王世铎

（沈阳建筑大学 交通与测绘工程学院，辽宁 沈阳 110168）

0 引言

近年来，网约车行业发展较快，相比于传统出租车，网约车服务更方便、快捷，但同样存在供需不均衡问题。对网约车需求聚类可以触发供给方的前瞻性调度行为，选择恰当的聚类算法提取和深入挖掘网约车订单数据的特征，将隐藏的时间需求分布交互性特征显性表达出来，有助于平衡供需关系，合理调度区域运力资源，更好地为乘客服务。

针对网约车需求，国内外学者多从数据挖掘角度研究其特征。张政等以网约车数据集为依据，提出了基于主题模型的出行需求识别方法，可较好地识别不同时间窗口下区域出行需求特征[1]。龙雪琴等以成都市网约车订单为基础，分析了工作日与非工作日网约车上下客的空间分布，证实网约车上下客热点具有明显的区域分布特性，且下客热点更为集中[2]。周梦杰等基于订单数据将居民出行的时间序列分解为空间模态和时间系数两部分，以挖掘乘客的出行特征[3]。Tang 等基于GPS 轨迹数据对出租车OD 点进行聚类分析，可有效识别出行热点区域[4]。He 通过网约车运营数据识别网约车的时空变化特征，证实网约车需求在不同时段内具有较强的规律性[5]。况东钰基于网约车数据对网约车需求进行时序分析，并识别了不同日期属性下需求量的变化规律[6]。

针对网约车时空聚类算法，现有研究多集中于聚类算法改进上。黎新华等提出一种将改进动态时间弯曲距离作为凝聚层次聚类相似性度量的聚类方法，相对于欧氏距离凝聚层次聚类而言，该算法能更好地识别网约车的时间需求变化特征[7]。林基艳等采用基于密度的聚类算法（Density-Based Spatial Clustering of Applications with Noise,DBSCAN）挖掘车辆行驶轨迹数据[8]，但该算法的参数选择对轨迹影响较大。基于此，孙立山等引入K-距离曲线对该算法进行改进并挖掘载客热点，提高了聚类精度[9]。Chen 等以网约车订单的初始经纬度作为特征值进行K-均值聚类，并以此进行区域划分[10]。崔宇超等采用K-均值（K-means）聚类方法对两类网约车订单数据进行聚类分析，发现两类乘客的出行需求呈相似特征[11]。但K-means 的聚类中心是随机选择的，易选到孤立点或选择的初始聚类中心距离较小，且K值较难确定，易导致聚类结果不稳定。Jian 等针对K-means 算法的缺陷进行改进，发现改进算法在出租车热需求方面具有更好的聚类效果[12]。除上述网约车聚类领域外，K-means 算法亦广泛应用在公交客流预测[13]、交通流时间序列预测[14]等其他交通预测领域中。

综上，现有网约车数据挖掘研究多集中在空间聚类领域，对网约车需求进行时间聚类分析的文献较少，且以往研究仅对一种数据模式的网约车需求变化特征进行分析，并未对不同数据模式的需求量变化规律的相似性和差异性进行挖掘。在聚类方法领域，研究重点主要集中在算法改进上，其中K-means 算法因其良好的聚类性能已被广泛应用，但该算法的聚类中心是随机选取的，且K值较难确定，易导致聚类结果不稳定。因此，本文将通过改进粒子群算法优化K-means 的初始聚类中心，并从时段特征和日特征两个角度对网约车需求数据进行聚类分析，以挖掘不同数据模式下网约车需求的变化规律，为网约车运营调度提供参考依据。

1 网约车需求分布特征

获取盖亚数据开放计划[15]中海口市2017 年5月22 日—6 月4 日共两周的网约车订单数据，分析网约车需求在一周内的分布特征，如图1所示。选取2017 年5 月22 日—5 月28 日一周的网约车数据，并将24h以10min为间隔，均匀划分为144个时间序列，分析工作日和非工作日的网约车需求分布特征，如图2 所示。由于多数样本的需求变化特征具有高度相似性，因此随机选取两周的样本数据，以分析网约车需求整体分布特征。

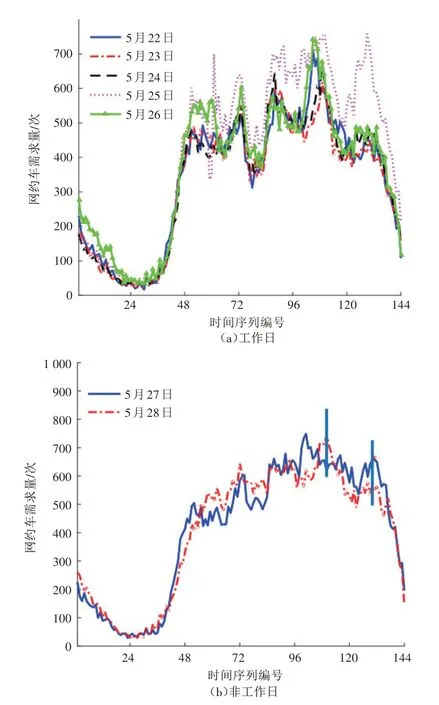
图2 网约车需求时段分布

由图1 可看出，网约车需求与星期属性有较大关系。网约车需求在一周的变化趋势为：周一至周三（5月22日—5月24日、5月29日—5月31日）网约车需求量较平稳，变化不明显；周四至周六（5 月25 日—5 月27 日、6 月1 日—6 月3 日）需求开始增加；周日开始下降。在一周中，非工作日的网约车需求显著高于工作日；在工作日中，周二（5 月23 日、5 月30 日）需求量较低，周四和周五（5 月25 日—5 月26 日和6 月1 日—6月2日）的需求量较高。在非工作日中，周六（5月27日、6月3日）的需求量略高于周日（5月28日、6月4日）的需求量。

由图2 可看出，工作日与非工作日的网约车需求时间分布存在较大差异，其中，工作日的时间序列分布具有较高相似性，且网约车需求变化幅度较大。工作日网约车需求一天内有4 个峰值，分别出现在早高峰时段8：20—8：30、午高峰时段11：50—12：00 和14：20—14：30、晚高峰时段17：20—18：00；非工作日网约车需求一天内有2 个峰值：一个较小的峰值和一个较大的峰值，这2 个峰值分别出现在18: 10 左右和21：30左右。

因此，如何识别不同数据模式下网约车需求时间序列变化的相似性与差异性，对挖掘网约车时间需求特征具有重要意义。

2 IDWPSO-K-means算法

K-means 是一种无监督聚类，可根据样本点的特征划分数据集，使得样本的多维分量在同组内相似，而在不同组之间相异，因此可以较好地识别不同时段和日期内网约车需求量时间序列变化的相似性和差异性。但由于K-means 聚类中心是随机选择的，易选到孤立点或选择的初始聚类中心距离较小，因此本文采用粒子群优化（Particle Swarm Optimization,PSO）算法优化K-means 的初始聚类中心。考虑到传统的PSO 算法存在早熟收敛等缺陷，不少学者对其进行了改进。其中，胡堂清等提出的动态调整惯性权重的改进粒子群算法（Hybrid Particle Swarm Optimization with Dynamic Adjustment of Inertial Weigh,IDWPSO）[16]，改进策略相对简单、收敛速度更快，具有较好的寻优性能。因此，本文采用该算法优化K-means的初始聚类中心。

2.1 K-means算法

MacQueen 于1967 年提出了K-means 聚类算法，用于处理数据挖掘中聚类相关问题[17]，其可将含有n个样本的集合x={x1,x2,…,xn}，划分成k个类簇ω1,ω2,…,ωk。算法的聚类步骤如下：

（1）确定需要生成的簇数k：从样本中抽取k个样本点作为k个原始聚类簇中心c1,c2,…,ck，即将x={x1,x2,…,xn}划分为k个类簇：ω1,ω2,…,ωk，其中

（2）计算非簇中心点xi与簇中心ci间的欧氏距离d[18]；

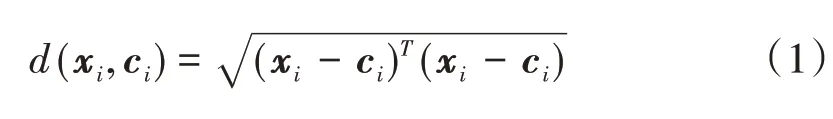
（3）根据欧氏距离矩阵，分配非初始簇中心样本点至距离最近的簇中心样本点所在的类；

（4）根据式（2）计算各类簇内样本的均值，并将该值作为新聚类中心[18]；

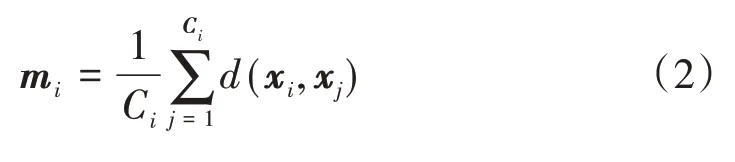
式（2）中：mi是簇i的中心；Ci是簇i的样本数目。

（5）重复步骤（2）～步骤（4），直至各类簇的样本点不再变化，迭代结束。此时输出的结果即为K-means聚类的最终结果。

2.2 IDWPSO算法

IDWPSO 主要在惯性权重和更新粒子位置两方面进行改进，具体如下。

（1）改进惯性权重

惯性权重ω通过指数函数控制，当迭代次数增加时，非线性减小，利用Matlab 中的betarnd 函数生成符合贝塔分布的随机数，以增强算法后期的全局搜索能力，其表达式为[16]：

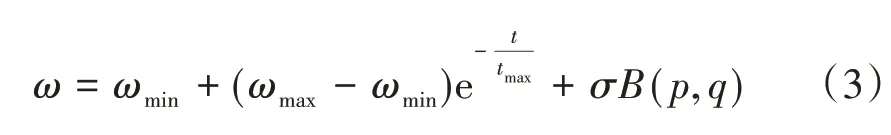
式（3）中：t为当前迭代次数；tmax是最大迭代次数；ωmax,ωmin分别为惯性权重的初值和终值；σ为惯性调整因子，取0.1；B(p,q)为贝塔函数。等号右侧第1 项与第2 项通过指数函数改变，算法前期惯性权重较大，随着迭代次数增加非线性递减。第3 项利用贝塔分布对ω的整体取值分布进行调整。

（2）粒子位置更新

引入差分进化操作更新粒子位置，以避免迭代后期种群多样性下降。其具体步骤为：初始化、变异、交叉和选择，通过变异与交叉操作更新粒子位置。位置更新计算式[16]为：

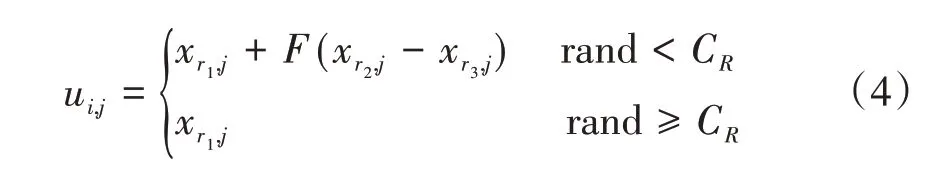
该算法的具体步骤如下：

①初始化种群参数；

②计算各粒子的适应度值；

③比较粒子个体适应度与群体最优值，选择更优者作为群体最优值；

④按式（3）计算惯性权重ω，并更新粒子速度；

⑤若rand ＜CR，采用交叉算子更新粒子位置，否则用PSO算法进行更新；

⑥当达到终止条件时，输出最优解，否则转至步骤②。

2.3 IDWPSO-K-means算法

据此，本文通过IDWPSO 算法优化K-means初始聚类中心的步骤如下。

（1）种群初始化，主要包含以下初始设置。

①设定粒子位置的最小值向量Zmin和最大值向量Zmax（其中Zmin和Zmax是依据所有样本点的各维分量的最小值和最大值所构成的向量而定），并设定粒子速度最大值Vmax。

②将数据集x中的n个样本点在k个簇中随机分配，按K-means 算法，根据式（2）计算k簇内的样本均值，将这k个均值作为聚类中心并以此构成一个粒子，不断重复该过程，直至生成m个粒子。设这m个粒子为，其中为粒子i的位置，是第i个粒子的第j个聚类中心（i=1,2,…,m;j=1,2,…,k）。

③原始m个粒子的适应度函数fitness[19]为：

式（5）中：fitness(Xi)为第i个粒子的适应度函数，其值越小，聚类质量越好。

④将粒子i的最优适应度Pbestfitness(i)的初值设为fitness(Xi(0))，最优位置Pxbesti的初值设为，i=1,2,…,m。

⑤将所有粒子中Pbestfitness(i)的最小者赋值在全局最优适应度Gbestfitness(i)上，将下标记为I，此时该粒子的对应位置PxbestI为全局最优位置Gxbest。

（2）生成下一代粒子群，根据式（6）～式（7）更新粒子i(i=1,2,…,m)的速度与位置，速度值在[-Vmax,Vmax]内，当rand ＜CR时，粒子位置更新算法采用式（4）中的交叉算子法，否则采用式（7）标准粒子群进行位置更新。

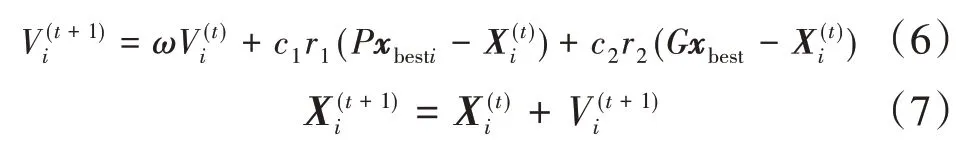
式（6）～式（7）中：ω为改进惯性权重，其计算方法如式（3）所示，可以权衡局部和全局最优能力；r1和r2为独立的随机变量，取值在(0,1)区间；c1和c2为加速系数，用来控制迭代步长，一般取值2.0[20]。

（5）找到所有粒子中最优适应度Pbestfitness(i)最小的值，作为全局最优适应度Gbestfitness(i)的值，并将该粒子的最优位置赋为全局最优位置Gxbest。

（6）若全局最优位置Gxbest在多次迭代后仍未变化，则退出迭代，转到（9）；否则继续运算。

（7）按式（8）降低惯性权重ω值[20]，式中参数含义同前。

（8）重复步骤（2）～步骤（7），直至迭代终止，转到步骤（9）。

（9）将粒子群全局最优位置Gxbest作为Kmeans 的聚类中心进行聚类，即重复执行以下几个步骤。

①将数据集x中样本点分配到离k个聚类中心Gxbest1,Gxbest2,…,Gxbestk最近的簇。

②重新计算k个簇中心。

③重复以上两步，直到k个簇中心无变化，或样本点未被重新分配，则迭代结束，转到步骤（10）。

（10）输出k个聚类中心，以及x的划分。

由于K-means 算法的难点在于事先确定类数k，因此本文预先设置多个k值，选取戴维森堡丁指数（Davies Bouldin Index,DBI）和标准偏差指数（Standard Deviation Based Index,STDI）[21]检验各k值下的聚类有效性，计算公式见式（9）和式（10），从而确定本文算法的聚类数目。

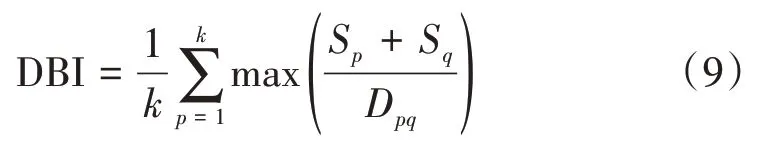
式（9）中：Sp和Sq为第p类和第q类内的元素与质心的标准差；Dpq为第p类和第q类质心间的欧氏距离；其他参数含义同前。式中括号内分子越小则类内元素相似度越大，分母越大则各聚类间相似度越小。因此，DBI值越小，聚类结果越有效。

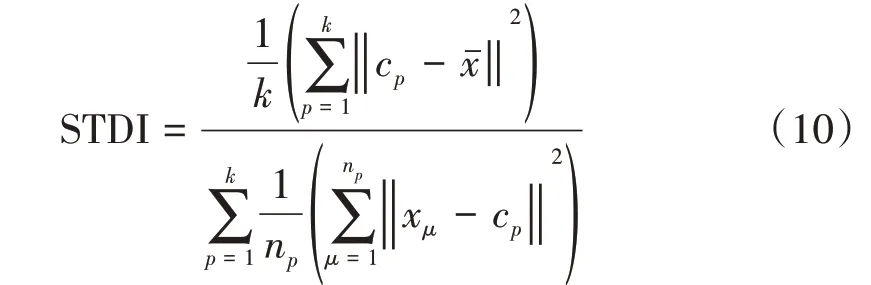
式（10）中：cp是类p的质心；是所有样本的质心；xμ是类p的第μ个样本；np是类p的样本数，k为类簇数。式中的分子表示各类之间的方差，分子越大，则各聚类间相似度越小；分母表示各类内的方差之和，分母越小，则类内元素相似度越大。因此，STDI值越大，聚类结果越有效。

3 实例分析

本文选取盖亚数据开放计划中海口市2017年5 月22 日（周一）至7 月21 日（周五）两个月的网约车订单数据进行分析，由于网约车需求变化特征不仅与一日内的时段有关，也与星期的变化有关，因此本文分别从时段和星期两个不同角度对网约车订单数据进行聚类分析，借助Matlab R2019a，基于IDWPSO-K-means 算法聚类分析网约车需求总量的时段特征和日特征。

3.1 基于时段特征的网约车需求聚类分析

本文将单个调查日按10min间隔共划分为144个时间序列，调查日总计61d，因此本文聚类算法的数据处理对象共144（个/d）×61（d）=8784（个）。当聚类数目为2～10时，其DBI和STDI见表1。

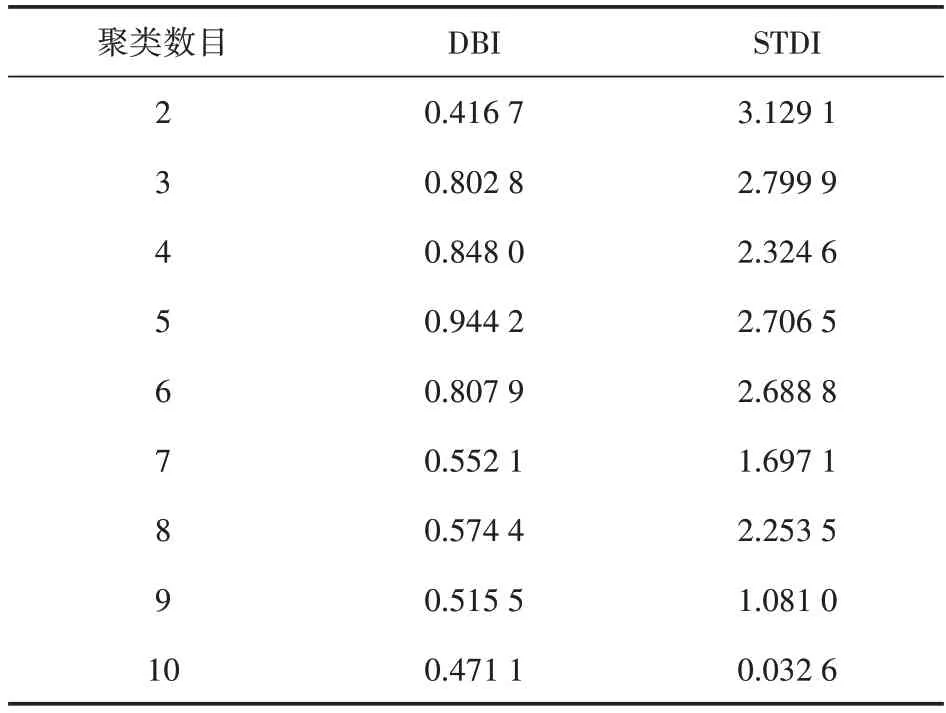
表1 基于时段特征的IDWPSO-K-means聚类检验系数

由表1 可看出，当聚类数目为2 时，DBI=0.4167,STDI=3.1291，同时达到最优，因此基于时段特征合适的聚类数目为2，聚类结果如表2所示。

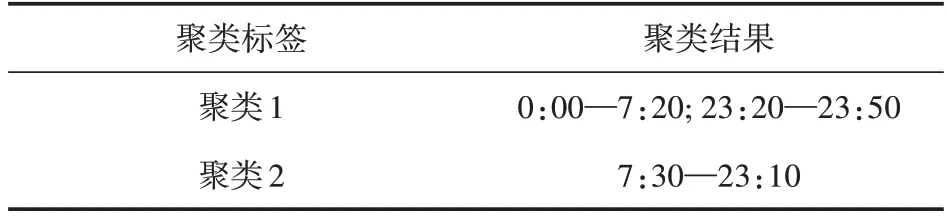
表2 基于时段特征的IDWPSO-K-means聚类结果

由表2可看出，IDWPSO-K-means算法将144个时段的需求量分为2 类，0：00—7：20 和23：20—23：50 均处于网约车需求较低的时段，7：30—23：10 网约车需求较高，与日常经验相似，分类较为合理。

3.2 基于日特征的网约车需求聚类分析

基于日特征聚类的数据模式与基于时段特征聚类相反，是对144 个时段中每个时段61d 的需求量进行聚类，观察同一时段每天需求量的变化情况。此处采用9：00—9：10的时段数据进行日特征聚类，聚类数目同样取2～10时，DBI和STDI如表3所示。

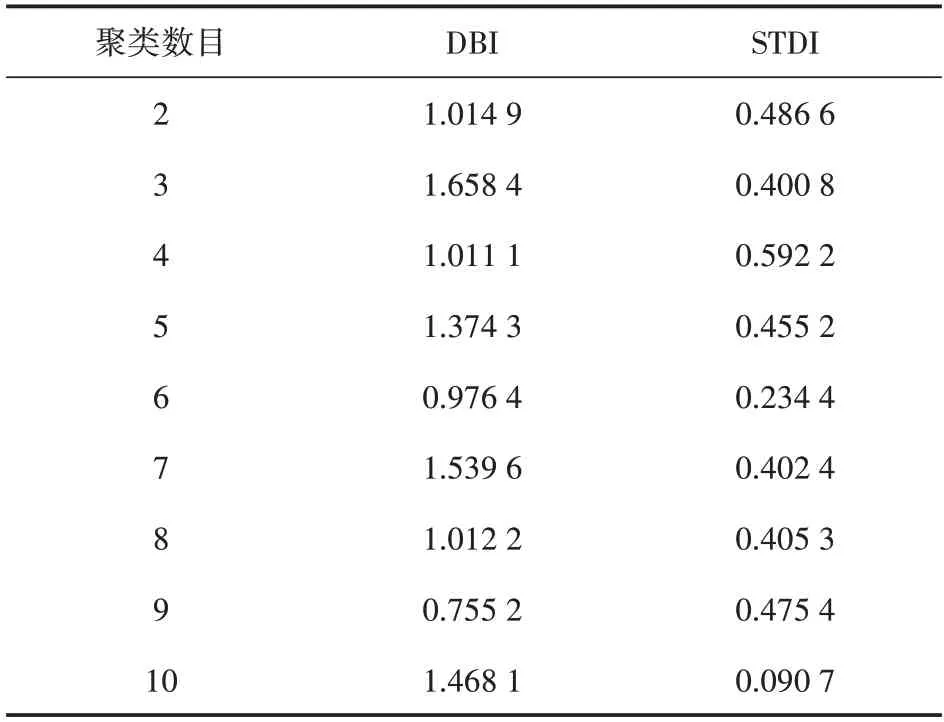
表3 基于日特征的IDWPSO-K-means聚类检验系数

由表3 可看出，当聚类数目为4 时，DBI 和STDI同时达到最优，因此基于日特征合适的聚类数目为4。当k=4时，聚类结果如表4所示。

表4 基于日特征的IDWPSO-K-means聚类结果

由表4 可知，IDWPSO-K-means 算法能较好地区分需求量不同的日期，同一时段中大部分周一至周三的需求量聚为稳定的一类、周五至周六大致聚为稳定的一类，与日常经验较为相似，工作日的出行需求略低于非工作日的出行需求，分类较为合理。个类别中将工作日和非工作日分为一类的原因是，个别工作日的网约车需求过高，与非工作日需求接近；或非工作日的需求量较低，与工作日的需求量接近，被看作异常的工作日或非工作日。

3.3 对比分析

为验证本文算法聚类效果的有效性，选用聚类误差平方和和迭代次数作为聚类评价指标，并与K-means 算法和PSO-K-means 算法进行对比。误差平方和s的计算公式[18]为

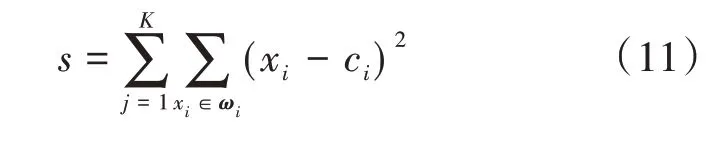
式（11）中：xi为样本点；ci为聚类中心；ωi为第i个样本集合；k为类簇数。

3.3.1 基于时段特征聚类的对比分析

根据式（11）计算当聚类数目为2～10时，基于时段特征聚类的3 种算法的误差平方和，结果如表5所示，迭代次数如表6所示。

表5 基于时段特征聚类的3种算法的误差平方和

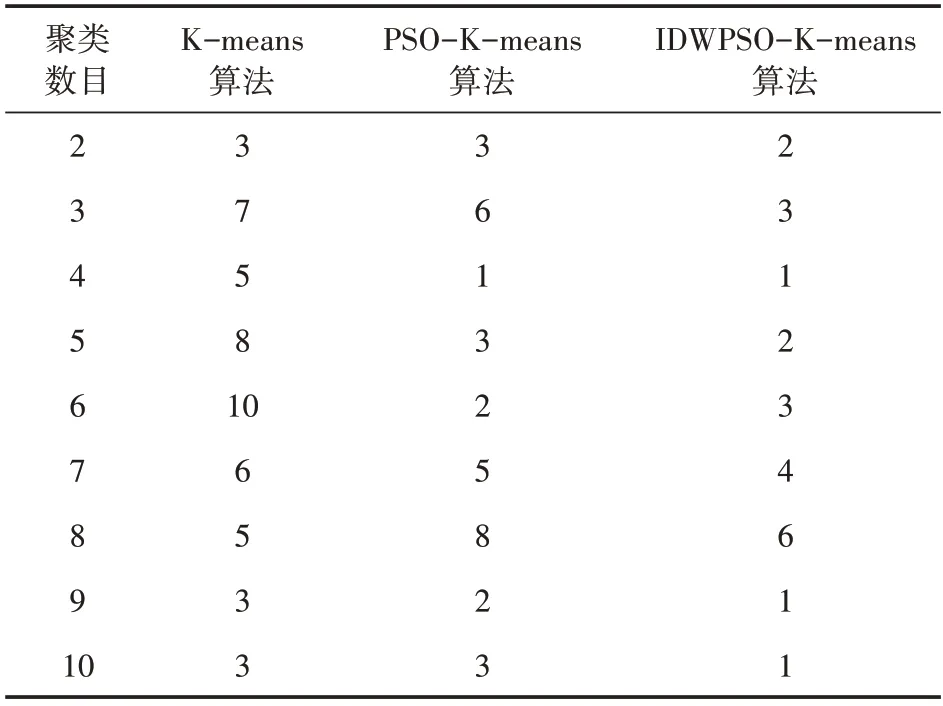
表6 基于时段特征聚类的3种算法的迭代次数

由表5 可看出，PSO-K-means 算法和IDWPSO-K-means 算法聚类结果的误差平方和在任意聚类数目下，均小于K-means 算法。当k=2 时，IDWPSO-K-means 算法和PSO-K-means 算法得到了相同的聚类中心和聚类数目，因此，误差平方和相等。仅当k=3 时，IDWPSO-K-means 误差平方和略大于PSO-K-means 算法。当k=4～10 时，IDWPSO-K-means 算法的误差平方和小于PSOK-means算法。

由表6 可看出，IDWPSO-K-means 算法和PSO-K-means 算法在聚类数目为8 时，迭代次数略高于K-means 算法；在聚类数目为6 时，IDWPSO-K-means 算法迭代次数略高于PSO-K-means算法，但低于K-means 算法；当聚类数目为2～5、7、9～10 时，IDWPSO-K-means 算法均有最小的迭代次数。

3.3.2 基于日特征聚类的对比分析

比较基于日特征聚类的3 种算法聚类结果的误差平方和及迭代次数，如表7和表8所示。

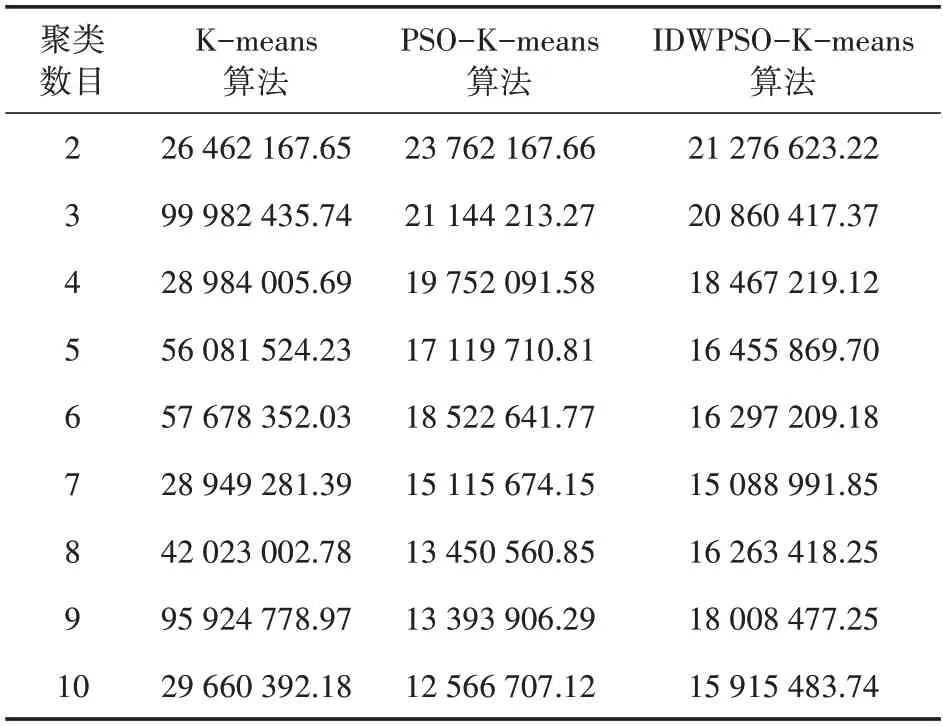
表7 基于日特征聚类的3种算法的误差平方和

表8 基于日特征聚类的3种算法的迭代次数

由表7 可看出，PSO-K-means 算法和IDWPSO-K-means 算法的误差平方和均小于K-means算法。当k=8～10时，IDWPSO-K-means 算法的误差平方和略大于PSO-K-means 算法；当k=2～7时，IDWPSO-K-means 算法误差平方和小于PSO-K-means算法。

由表8 可看出，IDWPSO-K-means 算法按日特征聚类时，当聚类数目为9 时，其迭代次数略高于PSO-K-means 算法，但当聚类数目为2～8 和10 时，IDWPSO-K-means 算法的迭代次数低于或等于PSO-K-means算法。

由此可看出，无论是基于时段特征还是日特征对网约车需求进行聚类，本文提出的IDWPSOK-means 算法的聚类效果均最优，验证了本文算法的有效性。

3.4 基于聚类结果的对策建议

基于时段特征考虑，IDWPSO-K-means 算法将144 个时间序列聚为2 类，较好地识别出了不同时段内网约车需求的规律性；聚类结果较好区分了网约车需求量的时间变化阶段，网约车运营商可基于此优化资源配置，实现运力的合理调度。当网约车需求量处于高峰时段时，运营商需增加车辆供给，以满足乘客的出行需求；当处于需求量低峰阶段时，运营商可适当降低车辆供给，以压缩成本支出，避免运力浪费，实现供需均衡。

基于日特征考虑，IDWPSO-K-means 算法将不同日期的需求量聚为4 类，其中，同一时段内大部分周一至周三被聚为稳定的一类（标签1），周五至周六被聚为稳定的一类（标签3），周日被聚为一类（标签4）。相同类别的网约车需求变化趋势具有较高相似性，网约车运行商可依据不同类别下的交通需求，合理规划网约车运营调度方案，实现合理的资源配置。针对个别星期属性在多类标签出现的情况，将其归为异常类别，如周四均匀出现在标签1与标签2中、周五出现在多类标签中等，运营商需探查网约车需求量在该日突变的主要原因，确定是由于调度决策失误、供需不均衡等内在因素造成，还是由于天气、大型活动等外在因素导致，以提升对异常需求量的处理水平。

4 结语

本文首先对网约车订单数据进行了预处理，分析了网约车需求量的时段和日分布特征。然后针对K-means 算法的不足，提出了一种动态调整惯性权重的粒子群优化（IDWPSO-K-means）聚类算法来优化K-means 的初始聚类中心。最后基于该算法考虑两种不同的数据模式（时段特征和日特征）对海口市的网约车需求数据进行聚类分析。结果表明，基于时段特征的网约车需求量聚为2 类，基于日特征的网约车需求量聚为4 类，相同类别的网约车需求变化趋势具有较高的相似性。与K-means 算法和PSO-K-means 算法相比，IDWPSO-K-means 算法的误差平方和和迭代次数2 个指标的值均更优，能更好地识别出需求量时变特征，为网约车实时调度和规划提供依据。但本文仅针对网约车时间序列进行了聚类研究，尚未对城市传统出租车需求展开研究，未来可综合挖掘不同时段和日期内网约车与传统出租车的需求变化规律，有助于更好地提升城市运输服务水平。