变水温工况下室内空调末端供热能力分析

邹海燕

（山东省淄博市博山区热力公司，山东 淄博 255200）

1 引言

逆卡诺循环为制冷理论，在此理论指导下，制冷性能系数与热源温度成反比，即热源温度越高，制冷性能越差。上述反比特征同样出现在热泵循环中，出水温度越高，则制热性能越差[1]。热冷负荷比值在某种意义上代表了建筑冷热负荷特征，但不同气候条件下的建筑在热冷负荷比上存在不同。若建筑内冷热负荷具有较大差异，则会导致室内空调末端出现供热富余情况，此时应根据实际情况控制供热能力，以此减少由室内空调引发的能源损耗。

2 搭建物理模型

为更好地探究室内空调末端在变水温工况下的供热能力，本文结合风机盘管展开讨论。本次所选择的风机盘管型号为FP-68。该风机盘管的额定工况风量参数为680 m3/h，供热量5.4 kW，供冷量3.6 k W。风机盘管在供冷工况下，其供水温度为7℃，回水温度12℃；在供热工况下，回水温度与供水温度分别为52.5℃、60℃[2]。为保障物理模型完整性，对表冷器相关结构参数进行确定，具体如表1所示。

表1 结构参数

3 分析定流量过程

3.1 修正系数

对风机盘管传热体系分解为3个阶段，即强制对流阶段、铜管导热阶段及空气外掠管束阶段，将3个阶段的热阻数值相加则为整个风机盘管的总热阻。在实际供热期间，铜管导热系数几乎不受水温变化影响，故在本次研究中将其忽略。进一步分析管内外对流换热系数，发现其与多个参数存在关联，即流体流速、密度、特征尺度、流体导热系数、动力黏度、比热容。此外，风侧、水侧的流体流速在定流量过程中不会发生变化，相应的传热参数同样不变，此时仅关注因温度变化而产生的物性参数变动情况，并需修正对流换热系数。

盘管液体冷却导致了温度降低，继而使液体黏度增大，对壁面对流换热系数起到了弱化效果，在系数修正期间，可将修正系数定义为0.25次幂的温度变化前后的动力黏度比值，即（u0/u）0.25，将式（1）努塞尔数Nu、式（2）雷诺数Re与盘管外空气被加热时所产生的对热换流系数关联式（式3）进行联立计算，此时可得当特征尺度与空气流速持续不变时，对流换热系数aw与λ/νn成正比，其中ν代指运动黏度，对不同空气温度条件下的λ/νn参数进行观察，不难看出，该参数在不同空气温度条件下的变化较小，此时可确定，外表面对流换热热阻基本不会受到空气温度变化的影响，可将其忽略不计，可将对流换热热阻看作定值。

式（1）～式（3）中，Nu为努塞尔数；C为比热容，取0.615，J/（kg·K）；Re为雷诺数；n为指数，取0.466；u为空气流速；l为特征尺度，取自外径数值；aw为外表面对流换热系数；λ为流体导热系数；ν为运动黏度。此外，外表面对流换热系数在不同温度条件下的变化情况如表2所示，其中管道外径均为0.01 m，即l特征尺度为0.01 m。。

表2 外表面对流换热系数在不同温度条件下的变化

3.2 迭代计算

将室内环境热负荷看作5.4 kW，冷负荷看作3.6 kW，风机盘管的供热量与供冷量在额定工况条件下可实现协调匹配。当建筑地点发生变化时，假设空调室内环境热负荷、冷负荷分别减小、不变，此时若空调风机盘管若为冷负荷选型，则会在冬季出现出力过剩的情况。此时，可将冬季供水温度调低，以此可缩减空气侧与盘管侧之间的平均温差，但因温度降低，同时减少了内表面对流换热系数，继而增大了热阻，在此情况下可减少风机盘管出力。在已知进风温度t1、供水温度tg、供热能力Q1的情况下可得出出风温度t2、回水温度th，进一步得出平均温差Δtm及供热量Q2，将供热能力Q1与供热量Q2对比，若两者差值小于0.1%，则代表迭代完成。若得出大于0.1%的结果，则需重新带入数值，再次计算，迭代公式见式（4）～式（6）。

式（4）～式（6）中，mw为水侧流量；ma为空气侧流量；K为传热系数；F为传热面积Ca为空气侧比热容；Cw为水侧比热容。确定供水温度后即可得出风机盘管所能适应的室内最大热冷负荷比。

3.3 结果分析

对定流量工况下的空调风机盘管供热能力进行分析，供水温度的降低会带动平均温差与60℃供水温度额定工况比值的减小，此时风机盘管的有效供热量将会降低。若温度降低，则增大液体动力黏度，减小对流换热系数及传热系数，该变化同样会减少风机盘管的有效供热量。若空调供水温度降低至30℃时，对应的室内最大热冷负荷比为0.32，这就代表若空调选择冷负荷风机盘管，在冬季运行时，风机盘管能够承担的最大热负荷低于32%的夏季冷负荷。此外，当水温处于35℃、40℃、45℃时，其最大热冷负荷比分别为0.50、0.69、0.89，故定流量状态下，空调末端最大热冷负荷区间为32%～89%。若供水温度已确定适宜，为避免出现空调供热富余过剩的情况，确定建筑热冷负荷比时，应找出最大热负荷、最小冷负荷的房间，依据该房间的热冷负荷比得出整个建筑的热冷负荷比，以此避免冬夏共用型风机盘管在实际运行时出现不必要的能源损耗。

4 分析变流量过程

4.1 传热系数

当供回水温差低于5℃时，可将室内空调风机盘管调节为流量可变、5℃恒定温差的状态，在风机盘管管径不变的条件下，热水流量与热负荷同步减小，此时管内流速逐渐降低，Re同样随之减小，流体流动状态将逐渐从旺盛湍流区转变为过渡区。计算风机盘管管内强制对流换热的Nu时，多运用式（7）进行计算，并运用式（8）可计算出内表面对流换热系数。

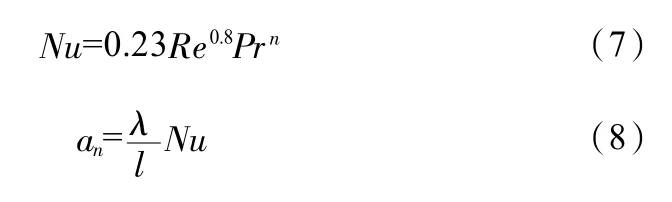
式（7）、式（8）中，Pr为普朗特数；l为特征尺度，取值为管径参数；n=3；λ为流体导热系数。

由于导热系数基本不受温度影响，故忽略不计，且风机盘管管束构造与流体流速并未发生改变，此时可将外表面对流换热热阻、导热热阻判定为定值，将两者相加即可得出额定工况时的总热阻与内表面换热热阻的差值。将内表面换热热阻、外表面换热热阻、导热热阻相加，其导数则为风机盘管传热系数。

4.2 迭代计算

在变流量工况条件下，进风温度t1、供水温度tg、回水温度th为已知条件，此时设定供热量为Q1，此时可得出出风温度t2、热水流量mw的数值，并可进一步计算得出对数平均温差Δtm，在明确热水流量参数情况下，可计算得出雷诺数及管内流速，同时引入普朗特数，计算得出Nu努塞尔数，继而得出内表面对流换热系数。

结合上述分析可见，确定对流换热系数后，可进一步得出综合传热系数参数，并将综合传热系数与对数平均温差进行运算，即可计算出实际供热量Q2。明确供热量Q1与Q2后，将其对比并计算差值，若两者之差小于0.1%，即为迭代完成，若差值大于0.1%，则需按照图1重新迭代计算，最终得出风机盘管变流量工况下的最大热冷负荷比结果如表3所示。

图1 迭代过程

表3 风机盘管变流量工况下的最大热冷负荷比结果

4.3 结果分析

根据表3即可直观清晰地明确风机盘管变流量工况下的最大热冷负荷比在不同供水温度下的变化情况。结合表3可知，当热水温度逐渐提升时，相对应的对数平均温差随之增大，同时会造成液体黏度减小，在此状态下，风机盘管内表面对流换热系数相应的增大。除此之外，当热水流量逐渐增大时，水流速度将根据热水流量情况而增大，此时风机盘管内表面对流换热系数将随之增大。在上述条件下，室内空调风机盘管实际供热能力将急剧上升，继而导致室内最大热冷负荷比高于定流量工况。当热水温度下降、热水流量下降时，上述状态将会呈现出相反表现，而该表现将会随着下降幅度的增大而变得愈发明显，将空调机组的供水温度调节至30℃时，最大热冷负荷比将会降低至15%，此时空调风机盘管需增大选型，成本将会提高，因此，本次工况变化研究仅用于数据分析，在现实生活中，可通过提高供水温度保障空调设备使用效益[3]。

4 结语

综上所述，选择风机盘管分析定流量、变流量工况下的空调末端供热能力变化，在分析期间搭建了物理模型，用于明确风机盘管结构参数，在此基础上结合多种参数，探究空调机组出水温度与室内冷热负荷比之间的关系，以此得出空调系统供热时最适宜的供回水温度，继而确保空调所表现出的供热能力能够与室内热冷负荷比相适宜，避免出现供热过剩、能源浪费现象。