软土地区高压输电线路杆塔抗拔承载力数值模拟研究
2022-08-24胡清晖陈彦宏
胡清晖,陈彦宏
(1.国网甘肃省电力公司兰州供电公司,甘肃 兰州 730070;2.国网甘肃省电力公司兰州新区供电公司,甘肃 兰州 730300)
随着大规模软土地区高压输电线路杆塔的使用,对输电线路塔杆的抗拉和抗拔能力也提出了更高的要求。目前,相关领域提出构建优化的软土地区高压输电线路杆塔抗拔承载力数值模拟模型,结合对抗拔承载力数值模拟和量化分析结果,进行大规模软土地区高压输电线路杆塔的承载力学分析,以此提高输电线路的稳定性和可靠性,研究大规模软土地区高压输电线路杆塔承载力学参数分析和可靠性建模方法,此技术在大规模软土地区高压输电线路的搭建和运维管理中都具有重要意义,相关的大规模软土地区高压输电线路杆塔的承载力数值模拟方法的深入研究近年来也受到人们极大关注[1]。
当前,对软土地区高压输电线路杆塔抗拔承载力数值模拟方法主要有基于特征融合和屈服响应的承载力拟合方法[2]、基于屈服强度特征分析的软土地区高压输电线路杆塔抗拔承载力数值模拟方法[3]以及基于自复位控制的软土地区高压输电线路杆塔抗拔承载力数值模拟方法等[4],以上传统方法通常先构建软土地区高压输电线路杆塔抗拔承载力力学分析模型,通过弹性力学参数分析方法,实现软土地区高压输电线路杆塔抗拔承载力数值模拟,但传统方法存在适应度水平不高,模拟精度不高问题。文献[5]针对架空输电线路工程杆塔基础的荷载特点和软土地区的特殊地质条件,开展了微型沉井基础在上拔、下压、水平、上拔与水平联合荷载工况下的承载特性真型试验研究。但是该方法无法获取承载力残余变形分布曲线,得到的抗拔承载力与实际数值出现偏差,无法得以广泛应用。
为改善传统方法应用过程存在的问题,本文提出基于荷载-应力屈服响应联合特征分析的软土地区高压输电线路杆塔抗拔承载力数值模拟方法。
1 高压输电线路杆塔抗拔承载力参数分析和特征检测
1.1 抗拔承载力参数分析
为实现软土地区高压输电线路杆塔抗拔承载力数值模拟,基于高压输电线路杆塔结构模型,构建软土地区高压输电线路杆塔抗拔承载力参数解析模型,高压输电线路杆塔结构基建结构如图1 所示,软土支撑力方向示意图如图2。
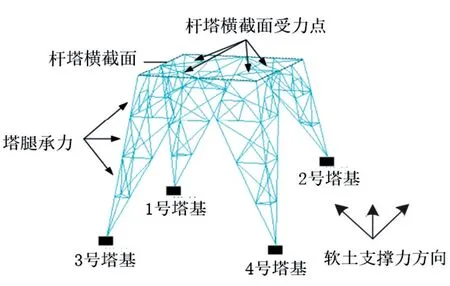
图1 高压输电线路杆塔结构基建结构

图2 软土支撑力方向示意图
在侧向荷载作用下,基于缩尺节点参数分析方法进行软土地区高压输电线路杆塔抗拔承载力参数模拟,通过不同配置数量滞回寻优控制方法进行软土地区高压输电线路杆塔抗拔承载力学的滞回响应特征分析[5]。
设定A为软土地区高压输电线路杆塔抗拔承载力原始参数值,B为侧向荷载值,n为数值的特征点数量,i为土体参数自相关性的时序,构建模糊方程得到高压输电线路杆塔抗拔承载力距离误差:
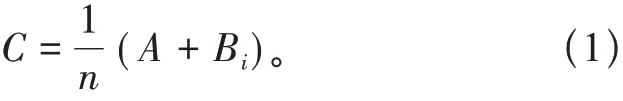
通过式(1)得出的距离误差,计算软土地区高压输电线路杆塔抗拔承载速率之差:
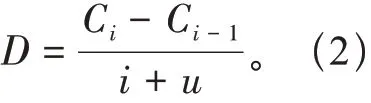
式中:u为更新时刻。
假设稳定参数分布权重为Wj,得到电线路杆塔抗拔承载力增量分布为
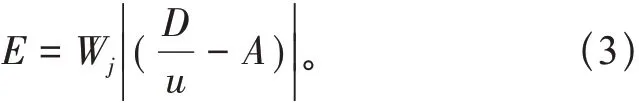
与式(3)所得增量代入动能参数计算式(4)得出软土地区高压输电线路杆塔抗拔的动能参数,用F表示[6]。
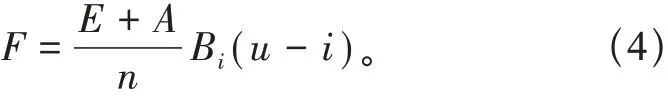
为构建软土地区高压输电线路杆塔抗拔承载的数值力学重构模型,用fi代表所得每一采样点所对应的抗拔承载动力参数并对其进行收集整理,数据集表示为
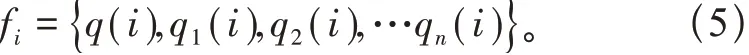
式中:fi表示参数随机场离散数值;q(i)为初步近似估计空间变异特征值;qj(i)为任意每个土体参数信息变化值,对所得fi采用中点法、局部平均法进行标定[7]得到输电线路杆塔抗拔承载力的数据捕获集合为
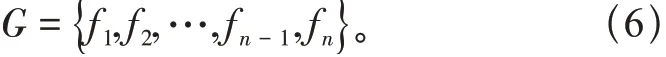
根据以上步骤完成抗拔承载力的参数分析。
1.2 高压输电线路杆塔抗拔承载力特征检测
通过不同配置数量滞回寻优控制方法进行软土地区高压输电线路杆塔抗拔承载力的滞回响应特征分析[8-10]。
假设k为高压输电线路杆塔抗拔承载力的采样时刻,fk为k时刻软土地区高压输电线路杆塔抗拔承载数据,通过线性插值方法进行软土地区高压输电线路杆塔抗拔承载力的拟合插值:

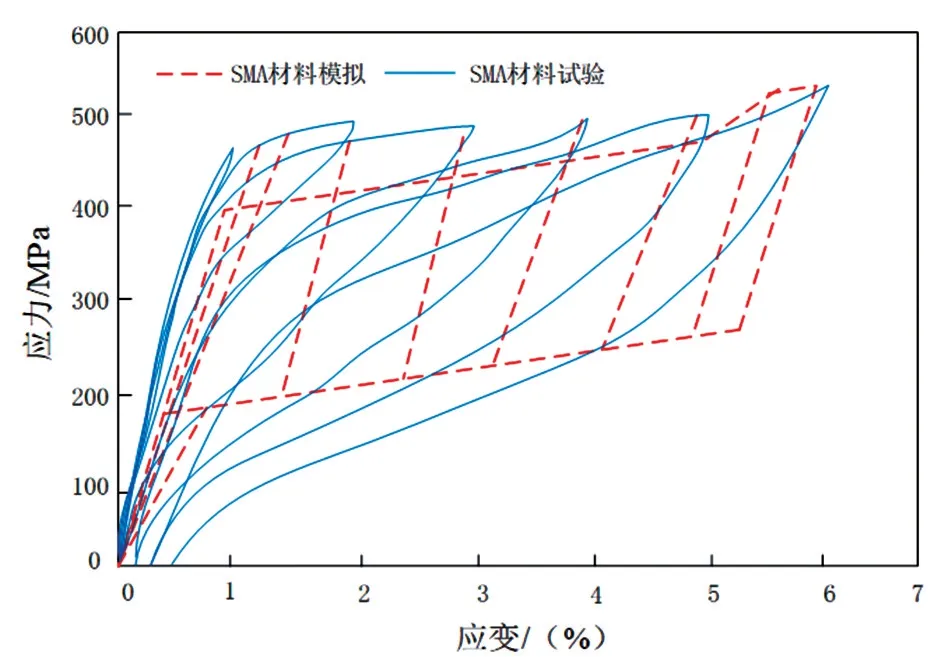
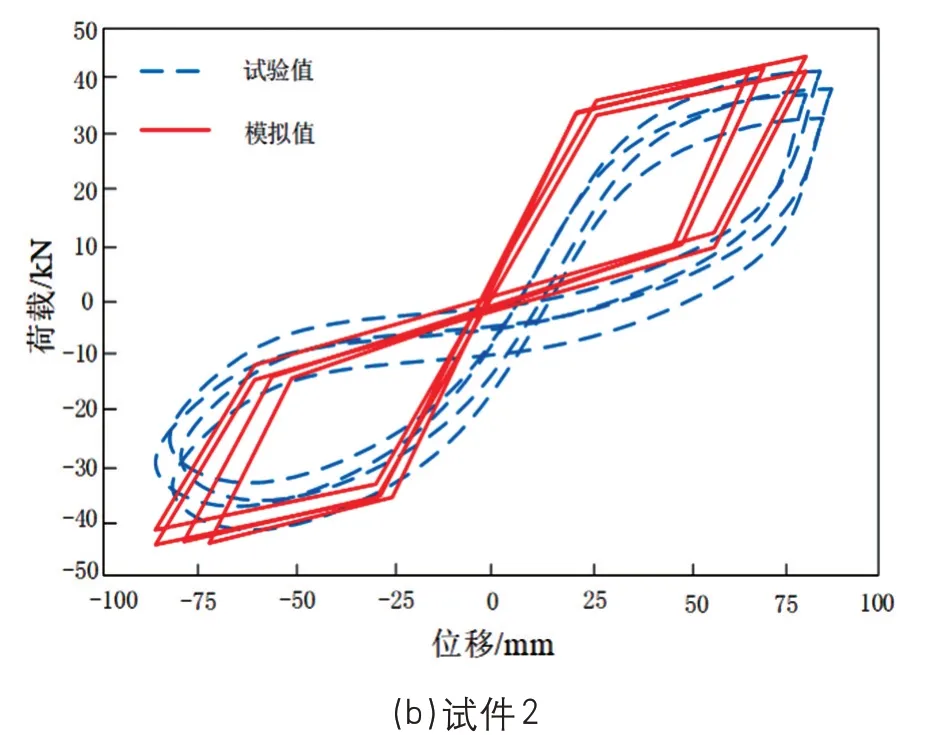
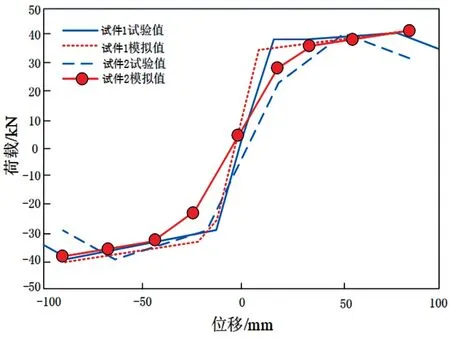
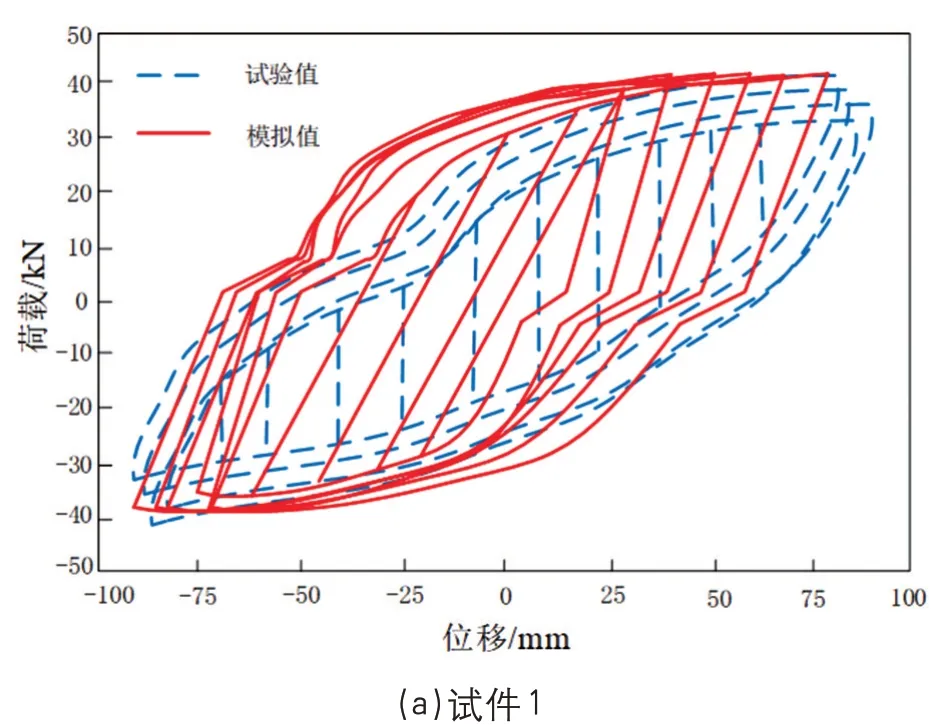
式中:K1 在独立标准正态空间中,检测高压输电线路杆塔抗拔承载力特征,以提高高压输电线路杆塔抗拔承载力数值模拟的精度。高压输电线路杆塔抗拔承载力精度的观测方程: 式中:a为高压输电线路杆塔抗拔承载力观测值;bk为k时刻高压输电线路杆塔抗拔承载力分布的四元数;r为力学参数规划值。 将观测精度值输入力学参数分析模型,得出高压输电线路杆塔抗拔承载力的数值模拟值: 通过I计算得出k时刻对高压输电线路杆塔抗拔承载力的数值模拟结果,实现动态特征分析[11]。 结合骨架曲线、电线路杆塔抗拔刚度退化曲线、承载力残余变形分布曲线联合分析的方法进行参数融合[12]。 通过土体参数自相关性和互相关性的相关分析,分析高压输电线路杆塔抗拔承载参数模拟值H。土体参数自相关系数为 式中:高压输电线路杆塔抗拔承载特性分布递归值为dk+1和hk+1或者mk+1和Ok+1;s为高压输电 线路杆塔抗拔承载力的观测扰动指数。 利用高压输电线路杆塔抗拔承载力数值模拟的自适应状态规划方程对得到的相关系数寻优[13],得到高压输电线路杆塔抗拔承载最优数据t: 式中:q为参考坐标系下的高压输电线路杆塔抗拔承载力的状态估计值;ν为约束二阶非线性特征量。 采用高压输电线路杆塔抗拔承载力参数融合的方法[14],得到高压输电线路杆塔抗拔承载控制的角度优化参数表示为 将q进行线性插值求得高压输电线路杆塔抗拔承载可靠度极限值Z为 通过分析高压输电线路杆塔抗拔承载可靠度极限值,可以构建概率密度模型为 融合高压输电线路杆塔抗拔承载力概率模型的数据,得出w随机样本对应概率为 对概率模型进行荷载-应力屈服响应联合特征分析[15],得到优化控制模型的表达形式: 式中:x为占用概率;y为软土地区高压输电线路杆塔抗拔承载力的动态参数数据量[16]。软土地区高压输电线路杆塔抗拔承载力数值模拟的标准化函数为 考虑极限状态函数约束下,软土地区高压输电线路杆塔抗拔承载的动态控制参数V为 综上分析,模拟软土地区高压输电线路杆塔抗拔承载力,提高输电线路杆塔抗拔承载力模拟模型的正确性和适用性。 通过试验仿真测试验证本文方法在实现软土地区高压输电线路杆塔抗拔承载力数值模拟中的应用性能。试验在国网山东省电力公司实验室大厅完成。基础模型采用钢制锚板基础,由锚板、加筋肋板、钢制立柱组成,其中:锚板材质为35#钢,呈正方形,宽度D= 0.30 m,厚度t= 0.03 m;钢制立柱材质为HRB400 螺纹钢,截面为圆形,直径d=0.04 m。所有模型基础埋深一致,均为0.5 m,如图3所示。 图3 试验用模型基础 设定软土地区高压输电线路杆塔抗拔承载力分布的修正系数为1.36,输电线路杆塔的抗压强度取36.8 MPa,屈服强度为489.08 MPa,弹性模量为57.8 GPa,每次加载均为500 kN。根据上述参数设定,得到软土地区高压输电线路杆塔抗拔承载力数值模拟的试验加载模型如图4所示。 图4 试验加载模型 在图4 所示的软土地区高压输电线路杆塔抗拔承载力数值模拟加载模型中,得到软土地区高压输电线路杆塔的应力监测结果如图5所示。 图5 软土地区高压输电线路杆塔的应力监测结果 由图5 测试结果可知,利用本文模拟方法得到的材料应力与实际试验应力数据基本一致,表明本文方法具有应用有效性。以图5 的软土地区高压输电线路杆塔的应力监测结果为基础,得到软土地区高压输电线路杆塔的抗拔承载力荷载分布如图6所示。 分析图6 得知,本文方法能高精准度实现对软土地区高压输电线路杆塔的承载力数值模拟,材料载荷分布情况与实际情况基本相符,满足该方法的应用要求。 图6 软土地区高压输电线路杆塔的抗拔承载分布 软土地区高压输电线路杆塔抗拔承载模拟值与试验值的对比结果如图7所示。 分析图7 得知,本文方法进行软土地区高压输电线路杆塔的抗拔承载数值模拟与试验值的拟合关系较好,具有较高的数值拟合精度,应用性能良好。 图7 软土地区高压输电线路杆塔抗拔承载模拟值与试验值 为量化分析杆塔抗拔承载力,本文提出基于荷载-应力屈服响应联合特征分析的软土地区高压输电线路杆塔抗拔承载力数值模拟方法。构建软土地区高压输电线路杆塔抗拔承载的数值力学重构模型,采用中点法、局部平均法进行力学特征标定,进行软土地区高压输电线路杆塔抗拔承载力的模拟,提高输电线路杆塔抗拔承载力模拟模型的正确性和适用性。研究得知,本文方法进行软土地区高压输电线路杆塔抗拔承载力数值模拟的精度较高,拟合性能较好。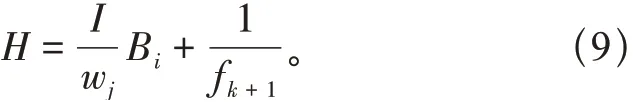
2 高压输电线路杆塔抗拔承载力数值模拟优化
2.1 参数融合
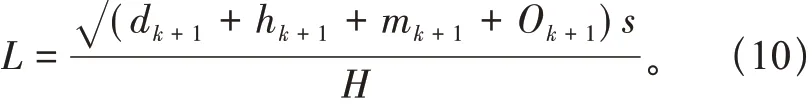
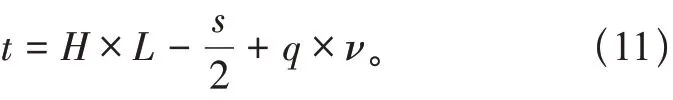
2.2 高压输电线路杆塔抗拔承载力模拟控制
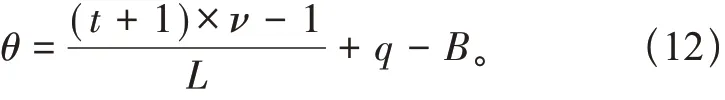
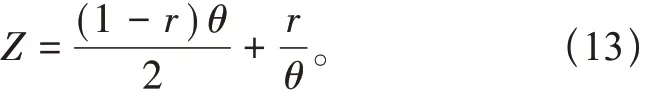
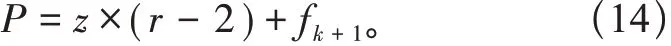

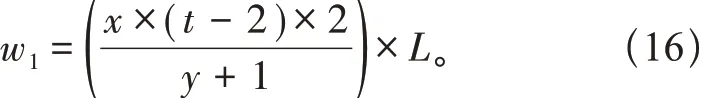

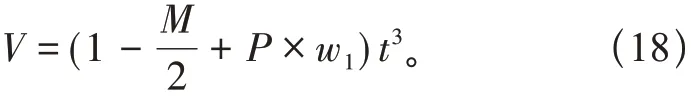
3 仿真测试分析


4 结束语
