Constructing Collective Signature Schemes Using Problem of Finding Roots Modulo

Tuan Nguyen Kim, Duy Ho Ngocand Nikolay A.Moldovyan

1School of Computer Science, Duy Tan University, Da Nang, Vietnam

2Department of Information Technology, Ha Noi, Vietnam

3ITMO University, St.Petersburg, Russia

Abstract: Digital signature schemes are often built based on the difficulty of the discrete logarithm problems, of the problem of factor analysis, of the problem of finding the roots modulo of large primes or a combination of the difficult problems mentioned above.In this paper, we use the new difficult problem, which is to find the wthroot in the finite ground field GF(p) to build representative collective signature schemes, but the chosen modulo p has a special structure distinct p = Nt0t1t2+ 1, where N is an even number and t0, t1, t2 are prime numbers of equal magnitude, about 80 bits.The characteristics of the proposed scheme are: i) The private key of each signer consists of 2 components (K1, K2), randomly selected, but the public key has only one component (Y) calculated by the formula; w1= t0t1 andw2= t0t2;andii)The generated signature consists of a set of 3 components(e, S1, S2).We use the technique of hiding the signer’s public key Y, which is the coefficient λ generated by the group nanager, in the process of forming the group signature and representative collective signature to enhance the privacy of all members of the signing collective.

Keywords: Computing roots; finding roots modulo; collective signature; signing collective; signing group

1 Introduction

Digital signatures [1] play an important role in authentication systems in today’s cyberspace.Other network security services such as ensuring the integrity of information transmitted on the network,preventing the disclaimer of responsibility of a communication partner, etc also need the support of digital signatures [2].It can be said that digital signatures contribute to making cyberspace safer and more reliable.Therefore, digital signatures and digital signature schemes are increasingly interested in research by cryptographic scientists.

Digital signatures is not only used to authenticate a single signer, but it can also support authentication for a collective, or a group, consisting of many different members.These people work together to create a single signature that represents an entire signing group or a group of signatures.Currently, there are many forms of digital signatures and digital signature schemes, in order to meet many different authentication models, which have been researched, published and applied in practice such as: Single digital signatures, group digital signatures [3-6], collective digital signatures [7-9], blind digital signatures [10,11], blind collective digital signatures [12], representative collective signatures[13].The types of signatures generated by a set of signers are often referred to as multi-signatures[14,15].

The group signature is a signature representing a signing group, the signature formation is controlled by the group manager, the group manager’s public key is used to verify the validity of the group signature of the signing group.The collective signature is a signature that represents a signing collective, signature formation is done by all members of the collective, the public key is used to check the validity of the collective signature is formed the public key of all members who participated in creating the signature.A collective signature on document M is considered valid when it is formed by the participation of all members of that signing collective.Representative collective signatures is a new formof collective signature, we rely on the advantages of the group signature scheme and the collective signature scheme to develop the representative collective signature scheme.

Arepresentative collective signature [8,9] is formed froma signing collective consisting of: i)Many groups of members, called signing groups, each group is represented by a group manager; and ii) A number of single individuals, known as individual signers, who do not belong to any group, but are functionally equivalent to the group leaders in this collective.Thus, a single representative collective signature can authenticate allmembers of amulti-level functional collective who are the creators of this representative collective signature.There are three difficult problems commonly used to build digital signature schemes, which are: i) The problem of parsing a composite number into prime factors [16]; ii) Discrete logarithm problem on prime finite field [17]; and iii) Discrete logarithm problem on Elliptic curves [18,19].

The problem of finding modulo roots in finite fields is a new difficult problem, introduced by Nikolay A.Moldovyan in [17].According to the author, the problem of finding thekthprime modulo root (with a prime modulo being a large primep, has the special structurep=Nk2+1, |p|≥1024, N being an even number and k is prime, |k|≥160) is a hard problem, the estimated difficulty isO.Digital signature schemes built on this difficult problem can achieve security level 280, however, the time cost of signature generation and signature checking is an issue that needs to be considered for improvement.According to Nikolay A.Moldovyan, this time cost limitation can be overcome if the difficult problem of finding prime modulo roots is considered in a finite field, with p having the following structurep=Nt0t1t2+ 1, where N is an even number;t0,t1,t2are prime numbers of the same magnitude as 80 bits.

The key pair of the signer in the case ofp=NK2+ 1 is (x,y), the private keyxis chosen at random, the public keyyis calculated by the formulay=xkmod p.But in casep=Nt0t1t2+1 is (K1,K2) andY).That is, the private key consists of two componentsK1andK2, the public key is still one component Y.This is the difference of the signature schemes described in this paper.

In this paper, we use the difficult problem of finding roots modulo in a finite ground field, with a prime modulopwith the structurep=Nt0t1t2+1 and a single signature scheme described by Nikolay A.Moldovyan in [20] to build the collective signature scheme and the group signature scheme.From these two basic schemes, we propose and build two types of representative collective signature scheme,proposed by us: i) The collective signature scheme for many signing groups (the RCS.01-3 scheme);and ii) The collective signature scheme for many signing groups and many individual signers (the RCS.02-3 scheme).These schemes fully inherit the security advantages of the newly created difficult problem and the attack resistance of the basic signature scheme built by Nikolay A.Moldovyan.

2 Constructing the Related Basis Digital Signature Schemes

In this part, we use the problem of finding roots modulo in the finite ground field, with modulo p with the structurep=Nt0t1t2+ 1 [20], to build a collective digital signature scheme and a group digital signature scheme.These are the two basic signature schemes that we use to build the proposed collective digital signature schemes.

2.1 The Collective Signature Scheme Based on Problem of Finding Roots Modulo (The CDS-2 Scheme)

Assume there is a collective ofmmembers who sign the document M.The private keys and public keys of each signer in this signing collective are (K1i,K2i),K1i＜p,K2i＜p, andYi=Kw11iKw22i, withw1=t0t1,w2=t0t2,t0≈t1≈t2≈80 bits andi= 1, 2,...,m.Note that the signer’s private key is a tuple of two components.

The collective public key used in the verification of the collective signature is calculated by the formulaY=∏mi=1Yimod p.FHis a pre-specified one-way secure hash function.

The process of checking the validity of a collective signature is the same as that of an individual signature [20].The following are the procedures of the scheme:

•The procedure for generating the collective digital signature on the document M

Includes the following stages:

1.Each i-thsigner performs the following steps:

- Generate pairs of random numbersT1iandT2i(act as a pseudo-secret key)

- Calculate the value ofRiaccording to the formula:

- SendRito all other signers in the signing collective

2.A certain signer, or all, in the signing collective does:

- Calculate the valueRaccording to the formula:

R acts as the general random component of the signing collective with the contribution of the random componentsRiof each member of this collective.

- Calculate the valueeaccording to the formula:

- Sendeto all other signers in the signing collective

eis the first element of the collective signature.

3.Each i-th signer goes on to:- Calculate their share signature componentS1iandS2iaccording to the formulas:

- SendS1iandS2ito all other signers in the signing collective

4.A certain signer, or all, in the signing collective does the final job: Calculate the second componentS1and the third componentS2of the collective signature according to the formulas:

So the triple value (e,S1,S2) is the collective signature of the signing collective consisting ofmsigners on document M.

•The procedure for verification the collective digital signature on the document M

To check the validity of the signature received with the document M, the verifier performs the following steps:

1.Calculate the value of the collective public keyYaccording to the formula:

2.Calculate the value ofR′according to the formula:

3.Calculate the value ofe′according to the formula:

4.Comparee′withe.Ife′=e: The received signature is valid; Otherwise, it is invalid and will be rejected.

•Proof of the correctness of the CDS-2 scheme:

To prove the correctness of this scheme, we need to prove the existence of the test expressione′=ein the signature checking procedure.

Conspicuously, the test expressione′=ealways exists.

Indeed:

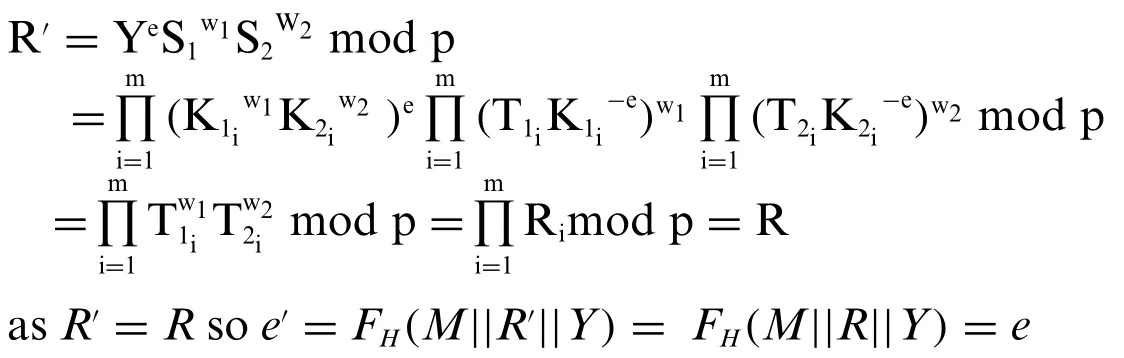
Thus, the test expressione′=ealways exists: This proves that the correctness of the signature check procedure, or the correctness of the CDS-2 scheme, is always guaranteed.

2.2 The Group Signature Scheme Based on Problem of Finding Roots Modulo (The GDS-2 Scheme)

Assume there is a group ofmmembers who sign the document M.The private keys and the public key of each signer in this signing group are (K1i,K2i),K1i＜p,K2i＜p, and, withw1=t0t1,w2=t0t2,t0≈t1≈t2≈80 bits andi= 1, 2,...,m.The private keys and the public key of the group manager (GM) are＜p,w1=t0t1,w2=t0t2and.

The group public key used in the verification of the group signature is calculated by the formulamod p.FHis a pre-specified one-way secure hash function.

The process of checking the validity of a group signature is the same as that of an individual signature [20].The following are the procedures of the scheme:

•The procedure for generating the group digital signature on the document M

Includes the following steps:

1.The GM does the following:

- Calculate the hash value of the document M using the formula:

- Calculate mask coefficients λifor each signer in the group sign according to the formula:

- Send λito each corresponding signeri

- Calculate the first component of the group signature

2.Each i-thsigner in the signing group does:

- Randomly generate pairs of numbersT1iandT2iand then calculateRiaccording to the formula:

- Send theRivalue to the group manager

3.The GM continues to make:

- Generates a random value pairandand calculate the valuesR′,Randeaccording to the formulas:

where δ is a prime number of length |δ| = 160 bits.

-eis the second component of the group signature.

- Send the value ofeto all signers in the signing group

4.Each signericontinues to do the following:

- Calculate the shared signature component ofS1i,S2iaccording to the formula:

- Send the valueS1i,S2ito other signers in the signing group

5.The GM does the final work:

- Check the correctness of the shared signatureS1i,S2iof all signers in the signing group using the formula:

- If all pairs of numbersS1i,S2iare satisfied: Calculate the signature component of a personal share according to the following formulas:

- Calculate the third componentS1and the fourthS2of the group signature according to the following formulas:

So the set of values (U,e,S1,S2) is the group signature of the signing group on the document M.

•The procedure for verification the group digital signature on the document M

To check the validity of the signature received with the document M, the verifier performs the following steps:

1.Calculate the value of the group public keyYaccording to the formula:

2.Calculate the value ofR*according to the formula:

3.Calculate the value ofe*according to the formula:

4.Compare the value ofe*withe.Ife*=e:The received signature is valid;Otherwise, the received signature is invalid, it is rejected.

•Proof of the correctness of the GDS-2 scheme:

To prove the correctness of this scheme, we only need to prove the existence of the check expressione*=ein the signature check procedure.

Conspicuously, the test expressione*=ealways exists.

We have:

So the expressione*=ealways exists: This proves that the correctness of the signature check procedure, or the correctness of the GDS-2 scheme, is always guaranteed.

3 Constructing the Proposed Collective Digital Signature Schemes Based on Problem of Finding Roots Modulo in the Finite Ground Field

In this section, we use the collective digital signature scheme and the group signature scheme described in Section 2 as the basis schemes to build two types of the proposed collective signature scheme:i)The collective digital signature scheme for many signing groups; and ii) The collective digital signature scheme for many signing groups and many individual signers.

3.1 Constructing the Collective Digital Signature Scheme for Signing Groups (The RCS.01-3 Scheme)

This section uses the two schemes just described above as the basis to build a representative collective signature scheme, the first type: The collective signature for many (g) signing groups.

This scheme allows the creation of a collective signature on the document M which represents a signing collective withgsigning groups, each of which consists ofmmembers, which is controlled by the group manager (GM).The signature formation process is run by the group managers.

The input parameters, public keys, and private keys are selected, calculated as the base schemes above.The following are the procedures of the scheme:

•The procedure for generating the collective digital signature for g signing groups on the document M

1.Each GM in the signing collective does the following:

- Calculate mask coefficients λjifor the signers in the j-thsigning group according to the formula:

(λjiis the mask coefficient of the i-thsigner in the j-thsigning group)

- Calculate the value of the componentUjof the j-thsigning group according to the formula:

Ujiis considered as the shared value of the j-thsigning group in the first component of the collective signature for the signing groups.

- Calculate the random componentRjusing the formula:

- SendUjandRjvalues to all other GMs in the signing collective

2.A certain GM in the singing collective, or all, computes the values of theU,Randecomponents of the collective signature according to the following formulas:

and

where δ is a large prime |δ| = 160 bits.

Uandeare the first and second components of the collective signature.

3.Each GM in the signing collective continues to do:

- Calculate the shared signatureS1j,S2jof the j-thsigning group according to the formula:

withSjiis the shared signature of the i-thindividual in the j-thgroup.

- SendS1j,S2jto other GMs in the signing collective

4.A certain GM in the signing collective, or all, does the following:

- Check the correctness of the shared signatureS1i,S2iof all signing groups in the signing collective using the formula:

- If allS1i,S2iare satisfied: Calculate the third and fourth componentsS1i,S2iof the collective signature according to the formulas:

So set of values (U,e,S1,S2) is the collective signature ofgsigning groups on the documentM.

•The procedure for verification the collective digital signature for g signing groups on the document M

To check the validity of the signature received with the document M, the verifier performs the following steps:

1.Calculate the collective public key of the signing collectiveYcolaccording to the formula:

2.Calculate the value of the random componentR*according to the formula:

3.Calculate the value ofe*according to the formula:

4.Comparee*withe.Ife*=e: The received signature is valid; Otherwise, the received signature is invalid, it is rejected.

•Proof of the correctness of the RCS.01-3 scheme:

The precision of this representative collective signature scheme is shown through: i) The existence of a shared signature verification formulaSjishared by the signing team leadersRj; and ii) Existence of the test expressione*=ein the signature check procedure.Specifically as follows:

a) Prove the correctness of the shared signature check formula:

It is easy to see that the formula for checking shared signatureSjishared by team leaders signingRjalways exists.Indeed:

b) Proof of correctness of the signature check procedure:

Conspicuously, the signature check expressione*=ealways exists.

We have:

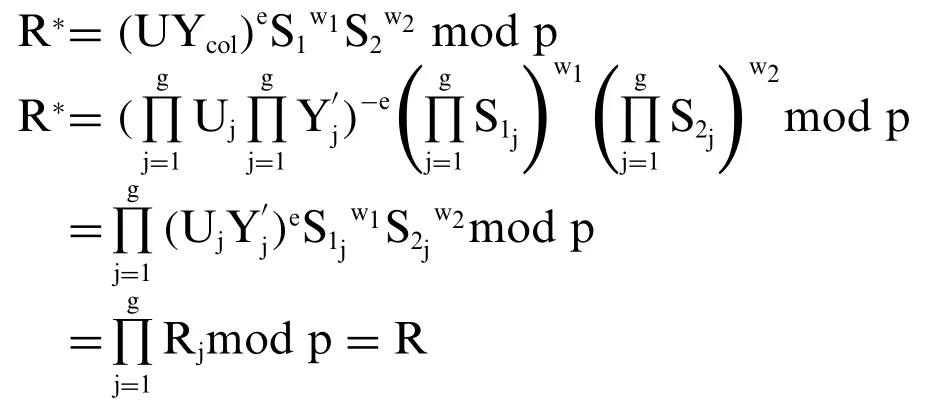
Because ofR*=Rsoe*=FH(M||R*||U) =FH(M||R||U) =e.

So the expressione*=ealways exists: This proves that the correctness of the signature check procedure is always guaranteed.

From (a) and (b): The correctness of the RCS.01-3 scheme is guaranteed.

3.2 Constructing the Collective Digital Signature Scheme for Signing Groups and Individual Signers(The RCS.02-3 Scheme)

This section uses the two schemes just described above as a basis to build a representative collective signature scheme, the second type: The collective signatures for many (g) signing groups andmany (m) individual signers.

This scheme allows the creation of a collective signature on document M that represents a signing collective with m individual signers and g signing groups, each of which consists of m members which is controlled by the group manager (GM).The signature formation process is run by the group managers and individual signers.

The input parameters, public keys, and private keys are selected, calculated as the base schemes above.The following are the procedures of the scheme:

•The procedure for generating the collective digital signature for g signing groups and m individual signers on the document M

Includes the following steps:

1a.Each GM in the signing collective does the following:

- Generate mask coefficient λjifor the signers in the j-thsigning group according to the formula (23).

(λjiis the mask coefficient of the i-thsigner in the j-thsigning group)

- Calculate the value of the componentUjof the j-thsign group according to the formula:

Ujis the shared member of the j-thsigning group to form the first part of the collective signature.

- Calculate the random parameterRjof the j-thsigned group according to the formula:

Rjis a shared member of the j-thsigning group to generate a random parameter of the collective signature..

- SendUjandRjvalues to all other managers and individual signers in the signing collective.

1b.Each individual who signs the j-thperforms the following tasks:

- Choose 2 random numbersT1jandT2jand calculate the random valueRjaccording to the formula:

- Send the valueRjto all signers GMs and other individual signers in the signing collective.

2.A GM or a certain individual signing in the collective calculates the values ofU,Randeaccording to the following formulas:

where δ is a large prime (|δ| = 160bits);Uj= 1 whenj=g+ 1,g+ 2, ...,g+m).

Uandeare the first and second components of the group signature.

3a.Each GM in the signing collective continues to do:

- Calculate the shared componentS1j,S2jof groupjaccording to the formula:

withS1ji,S2jiis the shared component of the i-thsigner in the j-thgroup.

- SendS1j,S2jfor GMs and other individual signers in the signing collective.

3b.Each individual signer in the signing collective continues to do:

(the j-th;j=g+ 1,g+ 2, ...,g+m)

- Calculate the share componentS1j,S2jaccording to the formula:

- SendS1j,S2jto other GMs and individual signers in the signing collective.

4.A GM or an individual in the signing collective doing:

- Check the validity of eachS1j,S2jaccording to the formulas:

withj= 1, 2, ...,g

and

withj=g+ 1,g+ 2, ...,g+m

- If all are satisfied: The third component of the group signature will be calculated according to the formulas:

So the set of values (U, e, S1,S2) is the representative collective signature of a collective consisting ofgsigning groups andmindividual signers on the document M.This type of signature is also known as collective signature shared by multiple groups and signed by many individuals.It represents this collective signing.

•The procedure for generating the collective digital signature for g signing groups and m individual signers on the document M

To check the validity of the signature received with the document M, the verifier performs the following steps:

1.Calculate the collective public key of the signing collective according to the formula:

2.Calculate the value of the random parameterR*according to the formula:

3.Calculatee*using to the formula:

4.Comparee*withe.Ife*=e: The signature received is valid; Otherwise, the received signature is invalid, it is rejected.

•Proof of the correctness of the RCS.02-3 scheme:

The precision of this representative collective signature scheme is shown through: i) The existence of a formula to check the shared signature Sjof each signing group; ii) The existence of the signature test formula shared Sjby each individual signerRand iii) The existence of the test expressione*=e.Specifically as follows:

a) The correctness of the formula to check the shared signature of each group leader:

It is easy to see that the formula for checking shared signatureSjishared by team leaders signingRjalways exists.Indeed:

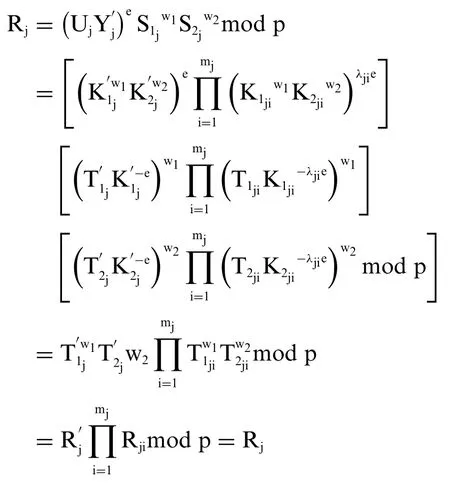
b) The correctness of the formula to check the shared signature per signer:

It is easy to see that the formula for checking the shared signatureSishared by theRsigning team leaders always exists.Indeed:

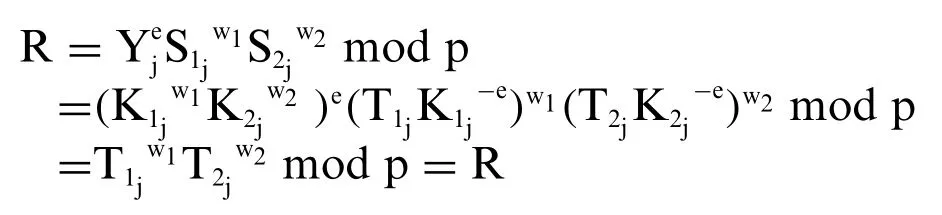
c) The correctness of the representative collective signature check procedure:

Conspicuously, the signature check expressione*=ealways exists.

We see:

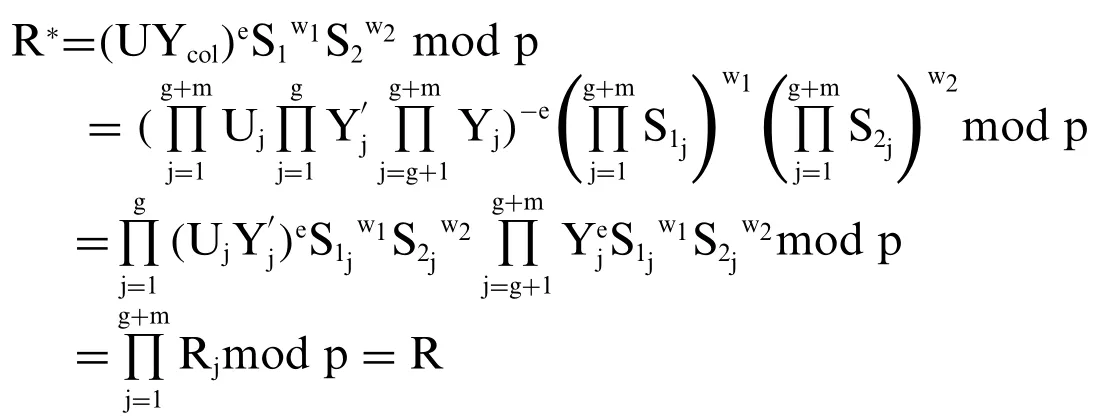
and calculate:

So the expressione*=ealways exists.This proves that the correctness of the signature check procedure, or the correctness of the RCS.02-3 scheme, is always guaranteed.

4 Security Analysis and Performance Evaluation

4.1 Security Advantages of the Proposed Collective Signature Schemes

The group signature scheme we described in Section 2.2 has the following security advantages:

•As the scheme is based on the properties of the prime modulo root problem in a finite field, it inherits the safety level of this difficult problem.The attack resistance of the GDS-2 scheme is completely similar to the basic scheme described by Nikolay A.Moldovyan in [20].To circumvent this scheme, the attacker must find the prime modulo roots to simultaneously determine the two secret valuesK1andK2.

•The public key of all signers, including the group manager, is“masked”by the mask parameter λ.The attacker will not be able to determine who in the signing group participated in the signing to form the group signature.

•The U component of the group signature contains information about all members of a signing group who took part in forming the group signature for this signing group.Consequently, when there is a dispute about the group signature, the group leader will be able to identify the signer easily later and resist the“disclaimer”.

•There is no need to exchange or share security values, private keys, or secret keys between members of a signing group or between members of a signing group with the manager.Therefore, the Internet environment is sufficient to implement this scheme.In addition, the scheme is also easy to deploy on top of existing PKI (Public Key Infrastructure) systems [21].

•As shown in the 5th step of the signature generation procedure, a group manager only proceeds when he or she believes or has verified that all signatures participating in creating the collective signature are valid.The operation generates the final component(S1,S2)of the group signature,by adding the shared signature of the group leader to the product of the shared signatures of all members.This makes it very hard to simulate member signings, or members signing each other’s signatures and also shows the representativeness as well as high responsibility of the team manager.

The representative collective signature schemes built in this paper use the CDS-2 collective signature scheme and the GDS-2 group signature scheme as the basic scheme, so it also has the advantages of security and resistance to attacks like these schemes.

4.2 Performance of the Proposed Collective Signature Schemes

We evaluate the computational performance of the proposed representative collective signature schemes by calculating the time cost that the scheme takes for the signature generation process(Signature generation procedure) and the need for the signature verification process (Signature verification procedure).The time costs of representative collective signature schemes proposed in this paper are shown in Tab.1.

Table 1: Time cost of the proposed collective signature scheme: RCS.01-3 and RCS.02-3

Notations:Th: Time cost of a hash operation inZp;Ts: Time cost of a scalar multiplication inZp;Tinv: Time cost of a inverse operation inZp;Te: Time cost of an exponent operation inZp;Tm:Time cost of a modular multiplication inZp.

According to [22]: Th≈Tm, Ts≈29Tm, Tinv≈240Tm, Te≈240Tm,Tsqrt≈290Tm.

Information from Tab.1 shows that the time cost for signature generation and signature checking of a proposed representative signature scheme is not much larger when compared to the new collective digital signature schemes in [8].

5 Disscusion

•The representative collective signature is a new form of collective digital signature, it was proposed by us in 2019 and has been built on many difficult problems and/or different digital signature standards.The research results of this paper show that the proposed scheme can be built on a customized form of a new difficult problem, the problem of finding roots modulo in a finite ground field, with a two-component private key.This proves that the availability of a representative collective signature scheme is very high.

•The signature generation procedure in the proposed representative collective signature scheme shows that it has all the security advantages of the collective signature generation procedure and the group signature generation procedure.This is one of the advantages of the representative collective signature schemes proposed by us.

•The basic requirement for multi-signature schemes is to record the information of everyone who participated in creating the signature of the group or the collective.This information is needed for the identification of the signer and against the signer’s“disclaimer of responsibility”in the future.The group signature schemes and the representative collective signature schemes built here have met this requirement, the signer information is contained in the first component of the signature, the U component.The algorithm to identify the signer from the information contained in the U has been described in [6].

•The use of the U-component of the representative collective signature is necessary, but this increases the signature size.This is considered a limitation of the proposed scheme.We have proposed and built a two-component representative collective signature scheme, but we can only implement the scheme based on discrete logarithm problems.We are working to build this improved scheme based on the problem of finding roots modulo large primes.

6 Conclusion

Thus, in this paper, we build a collective signature scheme and a group signature scheme using the single digital signature protocol described in [20] via a two-component private key (K1,K2).Based on their computational difficulty, all three schemes are formed in order to find the modulo root of a large prime, with a prime modulop=Nt0t1t2+ 1, in a finite ground field.

The two signature schemes described above can then be used as the basis for building two different types of collective signature schemes: i) The collective digital signature scheme for many signing groups; and ii) The collective digital signature scheme for many signing groups and many individual signers.These two schemes fully inherit the attack resistance of the single signature scheme in [20] and the difficulty of finding the modulo root in a finite prime field, so the security of the scheme is always guaranteed.For all schemes built in this study, if the chosen modulo is 1024 bits, their security level will be 80 bits.

In this paper, we analyze and evaluate the proposed schemes based on their security benefits and computational performance.In the future, the design of a collective signature scheme will be based on the computational difficulty of finding roots modulo on the elliptic curve.

Funding Statement:We received funding for this research from Duy Tan University,Danang,Vietnam.https://duytan.edu.vn/.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.