改进的三次修正DV-Hop定位算法
2022-08-24张晶,李煜
张 晶,李 煜
1(昆明理工大学 信息工程与自动化学院,昆明 650500)
2(云南枭润科技服务有限公司,昆明 650500)
3(昆明理工大学 云南省人工智能重点实验室,昆明 650500)
4(昆明理工大学 云南省计算机技术应用重点实验室,昆明 650500)
E-mail:1256058027@qq.com
1 引 言
在万物互联的物联网世界中,各种各样的传感器在其中扮演着不可或缺的角色,传感器能够对事物进行实时的监测,通过网络通信将有价值的信息再传递给人类[1].例如:对森林动物移动位置的监测、森林火灾检测、战争中敌军的行动位置等等.若无法清楚的了解事件发生的地点,大多数时候所获得的检测信息也就失去了价值,因此对于传感器定位位置的研究一直是传感器的一个研究重点[2].为此,国内外许多学者都花费了大量的人力物力在其定位问题的研究上,也均取得了一定的成功.
传感器是一种对体积、能耗和成本均严格要求的设备,因此对所有传感器均加装GPS定位模块是不现实的[3],而且传感器的位置一般采用飞机随机抛洒的方式,落点不确定,有的落点靠GPS也可能无法实现定位而必须得依靠算法.为此定位算法的研究成为传感器定位问题的关键.用尽可能低的成本完成位置的确定,也一直是评价算法的很重要指标.总体而言,定位算法分有两种[4],一种是对传感器添加一些额外设备完成在实际场景下对距离或角度等信息的测量,故这种算法被称为测距算法,另一种是无需对传感器添加任何额外设备,仅仅依靠网络间的连通性即可完成节点的定位,故这种算法被称为无需测距的算法,尽管这两者中测距算法对位置的估计更为精确,但是添加额外设备也使得节点成本增加、功耗增加,因此DV-Hop作为无需测距中的典型算法,近年来一直属于热门领域[5].
文献[6]对跳数设定阈值,并以此为依据将跳距划分为3种类别,对未知节点进行加权最小二乘求解,并对未知节点周围一跳范围内的锚节点进行二次求质心,将两种解取均值作为最终解,对精度有一定提升,但是该算法没有对一跳锚节点构成的拓扑结构进行分析,而采用所有锚节点进行求质心会增加误差的积累,文献[7]对跳距进行了优化,并对不同锚节点采用其自身跳距的距离计算方式,随后使用levy策略的粒子群算法对未知节点进行求解,虽使用仿生优化算法,但仍存在较大误差,为进一步对精度进行提高从而更有效的定位到事件发生点,本文提出一种3次修正的DV-Hop定位算法,是基于对DV-Hop算法的改进研究,本文对DV-Hop算法的主要改进点有:1)跳数的优化:由于每个节点芯片都具有RSSI测量功能,为此提出基于RSSI测距的跳数划分思想,将离散跳数连续化,得到更准确的跳数值;2)跳距计算的优化:由于锚节点计算跳距时,并没有考虑到误差正负的交替性,因此导致整体误差不能代表出各项误差最小化的缺点,为此提出采用平方误差适应度函数计算跳距的方式,且原始算法未能考虑到锚节点的跳数与距离的匹配关系,而笼统的将所有锚节点均视为同等重要进行最小化适应度函数的求解得到跳距,这会导致误差的传播,因此本文在此评定锚节点的距离与跳数的关系并以此作为权值对适应度函数进行最小化,进而求解锚节点跳距;3)锚节点的反馈:由于DV-Hop是一个依赖网络拓扑的算法,因此距未知节点最近的锚节点的误差信息能够对未知节点的估计坐标有进行校正的作用,本文采用一种新的锚节点误差反馈策略对未知节点位置进行第一次修正;4)采用泰勒展开式对未知节点进行优化:将使用锚节点误差修正之后的未知节点位置作为初始值,在其周围采用泰勒展开式进行寻优,得到二次修正后的未知节点位置,最后加入场景性限制条件,将定位的估计位置超出边界的部分限制在边界上,将小于零的部分限制为0,第3次修正未知节点位置,并将其值作为最终坐标.通过进行的大量实验数据表明,各阶段的改进算法均对未知节点坐标起到了减少误差的作用,且与文献[6]、文献[7]以及各阶段算法而言,本文算法表现十分优异.
2 原始DV-Hop算法
DV-Hop算法一般由3个主要部分构成[8]:
最小跳数值的获取[9].在节点的部署阶段,传感器锚节点将自身的id编号、位置信息、以及跳数值(起始跳数为0),打包为一个数据包进行洪泛传播.当节点第一次接收到各锚节点的数据包时,将接收到的数据包中的信息取出,将其跳数值加1后存入自身的路由表中,随后未知节点将该数据包洪泛给其它节点.若节点不是首次接收到该锚节点的数据包,则对其跳数加1后比对该跳数值与路由表中的跳数值,若小则更新路由表中跳数值,并将该跳数加1的数据包洪泛给其它节点,若大则舍弃该数据包.自此,所有节点均能获得对于各锚节点而言的最小跳数值.
锚节点平均跳距.以锚节点i为例,锚节点个数为N,计算其平均跳距采用无偏估计的方法,适应度函数[10]如下:
f=1N-1∑i≠j(di,j-HopSizei·hopi,j)
(1)
令f=0,则可以求出其平均跳距为:
HopSizei=∑i≠jdi,j∑i≠jhopi,j
(2)
其中,hopi,j为锚节点i与其他所有锚节点的跳数,且均有i≠j,di,j,为锚节点i距其他各锚节点的距离.
未知节点的位置估计[11].各锚节点对其跳距值进行传播,未知节点仅接收第1次接收到的跳距值,其余均舍弃,以便获得最近锚节点的拓扑一跳值,并以此对自身距各锚节点距离进行计算,以未知节点p为例,假设其首次接收到的是锚节点i的跳距值HopSizei,则如式(3)所示:
dp,j=HopSizei·hopp,j
(3)
其中,hopp,j是p距各锚节点的跳数,dp,j为其相对应的近似距离.随后,使用最大似然法列出方程[12],方程如式(4)所示:
(x-x1)2+(y-y1)2=d21
(x-x2)2+(y-y2)2=d22
⋮
(x-xm)2+(y-ym)2=d2m
(4)
其中,d1,d2,d3,…,dm为p距各锚节点的近似距离.
式(4)的矩阵表述为:AX=D,其中:
A=2(x1-xm)(y1-ym)
(x2-xm)(y1-ym)
⋮⋮
(xm-1-xm)(ym-1-xm)X=x
y
D=x21-x2n+y21-y2n+d2n-d21
x22-x2n+y22-y2n+d2n-d22
⋮
x2n-1-x2n+y2n-1-y2n+d2n-d2n-1
使用最小二乘[13]可以解得:X=(ATA)-1ATD.
3 改进的DV-Hop算法
3.1 基于RSSI测距的跳数修正
相对于以往的跳数取值方式,文献[14]采用的是多通信半径的思想,但是多通信半径的思想却会极大增加节点能耗,并且跳数的精确与否直接与预传播半径的划分程度相关,文献[15]采用二通信半径的思想,不能对跳数进行更精准的划分,并且这种划分随着通信半径的增加,跳数会越来越不准确.
为此本文采用RSSI测距的思想对跳数进行连续划分,使得离散跳数成为连续性跳数,但由于RSSI容易受到环境、噪声、多径传播等因素的干扰,本文首先对RSSI进行加权正态滤波优化,使用滤波后的距离对跳数进行连续性划分.
3.1.1 RSSI测距模型
RSSI是现在的最受欢迎测距算法之一,因为现在大多数传感器的芯片都具有测量RSSI强度的功能,无需对传感器添加任何其它额外的硬件设备即可完成对距离的估测,但是由于信号在现实传播过程中,并不是处于真空理想状态,自然会受到各种因素的干扰,因此选择一种合乎实际的模型直接关系到测距的准确与否.而实际中常用的模型主要为传播路径损耗模型,本文采用此模型进行距离的估测.信号传播模型[16]如下:
RSSIr(d)=RSSIr(d0)-10ηlgdd0+ζ
(5)
其中,RSSIr(d)为距发射点d处信号强度大小,RSSIr(d0)为距发射点d0处的信号强度大小,为参考信号强度,一般d0取为1m,且其值已知,ζ为高斯噪声,η为路径损耗指数.
3.1.2 加权正态滤波
由于信号在传播时,经常会受到环境、噪声、多径效应等干扰,因此节点接收到的信号值往往不是真实值,而是受到干扰的值,为此,本文采用加权正态分布对传感器接收到的信号值进行处理.其中正态分布为:
f(x)=12πσexp(-(x-u)22σ2)
(6)
u=1N∑Ni=1xi
(7)
σ=1N-1∑Ni=1(xi-u)2
(8)
其中,u为信号均值,σ为信号的标准差.
根据正态分布的3σ原则,可知信号分布在(u-σ,u+σ)范围内的概率为0.6526,本文取RSSI值处于该区间内的值作为有效值,规避不正常值对整体值的影响,并对该区间内的一系列有效值进行加权优化.
假设节点筛选出的一组有效值为(RSSI1,RSSI2,RSSI3,…,RSSIn),对其进行求平均运算得:
RSSIAVG=RSSI1+RSSI2+RSSI3+…+RSSInn
(9)
经加权处理之后的最终RSSI值为:
RSSIWeight=∑nk=1wk·RSSIk∑nk=1wk
(10)
wk=11+|RSSIk-RSSIAVG|
(11)
其中wk为各有效RSSI的权值.
经过加权正态处理,可以使节点获得更为精准的RSSI值,极大提高了测距的精度,将外界环境的影响降到最低.
3.1.3 RSSI测距的跳数修正方法
由于RSSI与距离的对应关系为:
d=10A-RSSIr(d)10η
(12)
其中,A为参考信号强度即RSSIr(1),为此,节点根据其修正的RSSIWeight计算出的距离为:
dweight=10A-RSSIWeight(d)10η
(13)
为此,修正的连续跳数为:dWeightR,其中R表示节点的通信半径距离.
3.2 跳距适应度函数的修正
原始DV-Hop算法在对跳距进行计算时,采取了无偏估计[17]的方式计算跳距,但这种方式未能考虑到误差是随机分布且正负相间,导致总体误差最小化并非能使各项误差最小化,为此本文采用平方误差函数作为适应度函数求解跳距,如式(14)所示:
f2=1N-1∑i≠j(di,j-HopSizei·hopij)2
(14)
其中,di,j为锚节点i距其他所有锚节点之间的真实距离,N为锚节点个数,hopi,j为其相应的跳数最小值,且均有i≠j.
使f2对HopSizei求偏导数,并令其值为0:
∂f2∂HopSizei=0
(15)
可以解得,跳距值为:
HopSizei=∑i≠j(hopij·di,j)∑i≠jhop2ij
(16)
尽管如此,在对锚节点跳距计算时,此适应度函数也并未考虑到锚节点距离与跳数之间的匹配关系,如图1锚节点分布.

图1 锚节点分布图Fig.1 Distribution diagram of anchor nodes
锚节点i与锚节点a、b、c之间的距离均大约为节点通信半径距离R,然而节点i与节点a、b、c之间的跳数约分别为hi,a、hi,a+ha,b和hi,c.若采取同样眼光看待这种锚节点关系,则会对锚节点的跳距计算产生很大的误差,本文采用跳数-距离匹配因子αi,j来对平方误差适应度函数进行修正,其中:
αi,j=di,j/hi,j
(17)
这种跳数-距离匹配因子可以让距离与跳数不匹配的锚节点在参与计算跳距时所分配的权重值更小,如图1中,在计算锚节点i的跳距时,给锚节点a、b、c所分配的权重分别为:
αi,a=di,a/hi,aαi,b=di,b/(hi,a+ha,b)αi,c=di,c/hi,c
因此,跳距的计算方式为如式(18)所示:
f2=1N-1∑i≠jα2i,j(di,j-HopSizei·hopij)2
(18)
同样的,令∂f2/∂HopSizei=0,可以解得:
HopSizei=∑i≠jα2i,j·hopij·di,j∑i≠jα2i,j·hop2ij
(19)
3.3 锚节点误差反馈策略
DV-Hop是一个依赖拓扑结构的算法[18],且传感器在分布时,一般采取随机抛洒的方式,因此节点分布一般基本是随机均匀分布的.根据DV-Hop的定位特点,未知节点跳距采取最近锚节点传播的形式[19],因此越接近待定位节点的锚节点,节点之间的拓扑形式越相似,用同样方式,定位锚节点和定位未知节点之间的误差也越接近.于是本文提出一种锚节点误差反馈策略对未知节点估计位置进行修正.
使用改进后的跳数、跳距对锚节点的位置进行估计,假设锚节点的估计坐标为(,),真实坐标为(x,y),据此可以得到锚节点估计坐标与实际坐标的偏差值为:
Bx=-x
By=-y
(20)
随后锚节点将此偏差值与其锚节点id打包成数据包,进行洪泛传播.
未知节点对偏差值的接收规则为:
若未知节点通信范围内存在大于等于3个的锚节点,则将所有该范围锚节点偏差值的平均作为该未知节点的校正值.
若未知节点通信范围内锚节点数小于3,则将距该未知节点最近的3个锚节点的加权偏差值作为其校正值.对此未知节点仅接收3个不同锚节点id传来的偏差值,存储在自身路由表中,并将其继续洪泛传播给其邻节点,其余偏差值均舍弃,对接收到的3个与其最近的锚节点的偏差值进行加权作为自身定位的校正值,因为在实际传感网络中,相距较远的锚节点的定位偏差是毫无意义的,引入较远锚节点的偏差不仅会增加节点自身的计算量,也会带入误差,为此本文仅选择3个最近锚节点的加权偏差值作为未知节点的校正值.
假设未知节点接收到的3个最近锚节点分别为i,j,k,且其偏差值分别为(Bi,x,Bi,y),(Bj,x,Bj,y),(Bk,x,Bk,y),则该节点的校正值为:
x=∑kq=i(Wq×Bq,x)
y=∑kq=i(Wq×Bq,y)
(21)
其中,Wq=1/dp,q∑kq=i1dp,q,dp,q为改进的距离.
假定未知节点使用改进后的跳数、跳距值,得到的自身估计位置为(p,p),则可得到其第1次的修正位置(x,y)为:
x=p-x
y=p-y
(22)
3.4 泰勒中值定理寻优与场景限制
在传统算法中,极大似然估计方程的求解采用的是最小二乘的方式,然而最小二乘无法对未知节点进行更准确的求解,在矩阵ATA接近奇异时,也包含了很大的误差,为此,本文提出使用泰勒展开修正未知节点坐标的方法,将使用优化跳数、跳距、锚节点修正后计算出的未知节点坐标作为展开点对未知节点位置进一步修正,未知节点方程式(23)如下:
(x-x1)2+(y-y1)2=d21
(x-x2)2+(y-y2)2=d22
⋮
(x-xm)2+(y-ym)2=d2m
(23)
其中方程左边部分为:
f(x,y)=(x-xn)2+(y-yn)2
(24)
且n为1,2,3,…,m,m为锚节点数.
将f(x,y)在修正后的未知节点附近使用泰勒展开进行二次修正,假设经过一次修正后的未知节点坐标为(x0,y0),则可以得出:
f(x,y)=f(x0,y0)+(x-x0)f′x(x0,y0)+
(y-y0)f′y(x0,y0)+o(n)
(25)
其中令,α=(x-x0),β=(y-y0),为避免庞大的计算量,为此省略无穷小项o(n),则上式变为:
f(x,y)=f(x0,y0)+αf′x(x0,y0)+βf′y(x0,y0)
=(x0-xn)2+(y0-yn)2+2α(x0-xn)+2β(y0-yn)
(26)
将上式代入式(23)左边项,得出方程组(27)为:
2α(x0-x1)+2β(y0-y1)=d21-(x0-x1)2-(y0-y1)2
2α(x0-x2)+2β(y0-y2)=d22-(x0-x2)2-(y0-y2)2
⋮
2α(x0-xm)+2β(y0-ym)=d2m-(x0-xm)2-(y0-ym)2
(27)
式(27)方程的矩阵形式表示为:
A=2(x0-x1)2(y0-y1)
2(x0-x2)2(y0-y2)
⋮⋮
2(x0-xm)2(y0-ym)X=α
β
B=d21-(x0-x1)2-(y0-y1)2
d22-(x0-x2)2-(y0-y2)2
⋮
d2m-(x0-xm)2-(y0-ym)2
即:AX=B.
使用最小二乘法求解方程组得出X=(ATA)-1ATB,若α2+β2>Q,其中Q为某一较小临界值,则令:
x0=x0+α/3
y0=y0+β/3
(28)
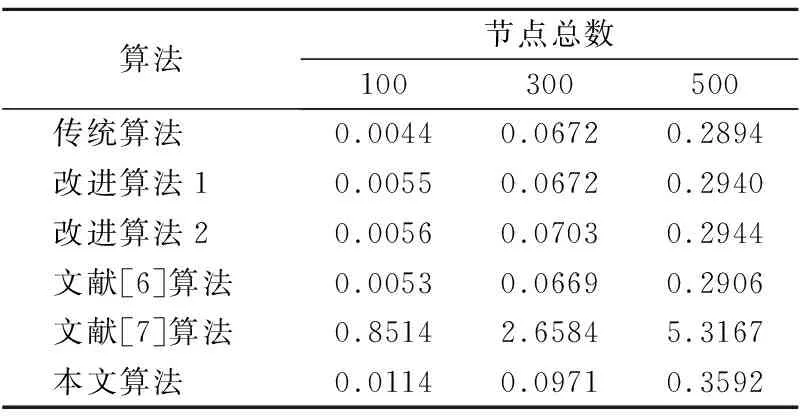
将(x0,y0)代入式(27)重新计算其α、β,直到α、β满足α2+β2 最后,对于实际应用场景下,节点一般部署于某一块区域内,且从理论出发,节点的定位坐标不应超出边界或小于0值,于是,本文算法对于二次修正的未知节点定位坐标加入场景性限制条件,将未知节点估计坐标大于边界值的值,限制为边界值,小于0的坐标值,限制为0.自此完成对未知节点的第3次修正. 本文算法的具体实施过程如下: Step 1.锚节点利用洪泛的方式将包含自身id、初始为0的跳数值、与地理坐标信息的数据包进行传播.各节点通过相邻节点间接收到的一系列RSSI值,经加权正态滤波得到其修正的RSSIWeight,根据计算出的距离得到其修正的连续跳数值.洪泛结束后,各节点获得与其它锚节点的最小跳数值. Step 2.各锚节点利用加权的适应度对跳距进行计算,并利用该跳距和连续跳数估算与其它锚节点距离,随后利用多边定位的方法进行自身坐标的估计,并计算出偏差值. Step 3.锚节点将自身定位偏差打包成数据包进行洪泛,未知节点根据接收规则计算自身校正值. Step 4.未知节点也使用改进的跳数、跳距计算自身坐标,并与校正值相减得到未知节点第1次修正的坐标. Step 5.将第一次修正的未知节点坐标作为泰勒展开式的展开点代入方程组中进行第2次修正,当达到循环退出条件的精度,则退出循环体,并将其最终坐标作为第2次的修正坐标,完成对未知节点的第2次修正. Step 6.将二次修正后的坐标加入场景限制,对不合法的节点位置进行校正,得到其第3次修正后的位置坐标.自此完成坐标的定位. 为评估本文算法与传统DV-Hop算法和各改进算法之间性能的差距,所有试验均设计在matlab 2016平台上进行仿真验证,其中改进算法1采用本文锚节点误差反馈、最小二乘法的第1次修正策略,改进算法2采用本文跳数、跳距优化改进、锚节点误差反馈、最小二乘法的改进的第1次修正策略,本文算法采用跳数、跳距优化、锚节点误差反馈、泰勒寻优、和场景性限制条件的改进的3次修正策略,以及文献[6]和文献[7]的改进算法,进行对比实验,节点部署于100×100范围内,且各节点均随机分布,算法仿真性能采用未知节点的平均误差作为评价算法优劣的标准[20],平均误差越低代表网络中节点的定位越准确,如式(29)所示: Avg_error=∑ni=1(xi-x′i)2+(yi-y′i)2n×R (29) 图2 实验模拟图Fig.2 Experimental simulation diagram 其中n为测试中未知节点的数量,(xi,yi)为其实际位置,(x′i,y′i)为通过算法估计出的位置,实验模拟图如图2所示. 在边长均为100×100的矩形内,设置节点总数为200,其中的锚节点比例变化趋势为0.1、0.15、0.2、0.25、0.3、0.35、0.4、0.45、0.5,节点通信范围均设置为40m,每次实验结果对其取100次的均值,观察6种算法对未知节点定位的准确度. 从图3中可以看出,在同一仿真条件下,在锚节点比例为0.1时,本文算法相对传统算法、改进算法1、改进算法2、文献[6]与文献[7]算法的误差降低了[0.2221,0.1599,0.0561,0.1476,0.1227],在锚节点比例为0.3时,本文算法相对传统算法、改进算法1、改进算法2、文献[6]与文献[7]算法的误差降低了[0.2407,0.1544,0.0597,0.1364,0.105],在锚节点比例为0.5时,本文算法相对传统算法、改进算法1、改进算法2、文献[6]与文献[7]算法的误差降低了[0.2442,0.1535,0.0616,0.1216,0.0852].由此可以得出,传统算法的定位误差在整个变化过程中几乎变化不大,始终处于比较高的水平,改进算法1、改进算法2、文献[6]、文献[7]以及本文算法均随着锚节点比例的增加,误差有所降低,且本文算法即使在锚节点个数较低时,依然拥有较好的定位精度,对于未知节点而言,这一特点也使得该算法在一定程度上能够减少布设时锚节点的数量,从而降低传感网络的造价. 图3 锚节点比例与平均误差的变化趋势图Fig.3 Trend chart of anchor nodes ratio and average error 在边长均为100×100的矩形内,设置节点总数为200,其中锚节点比例为0.25,节点通信范围的变化趋势为30、35、40、45、50、55、60、65、70,每次实验结果对其取100次的均值,观察6种算法对未知节点定位的准确度. 图4 通信范围与平均误差的变化趋势图Fig.4 Trend chart of communication range and average error 从图4中可以看出,在同一仿真条件下,在节点通信半径为30m时,本文算法相对传统算法、改进算法1、改进算法2、文献[6]与文献[7]算法的误差降低了[0.2244,0.1571,0.0561,0.1477,0.1198],在节点通信半径为50m时,本文算法相对传统算法、改进算法1、改进算法2、文献[6]与文献[7]算法的误差降低了[0.247,0.1503,0.0584,0.1274,0.098],在节点通信半径为70m时,本文算法相对传统算法、改进算法1、改进算法2、文献[6]与文献[7]算法的误差降低了[0.2028,0.1249,0.0518,0.1109,0.0799],由此可以得出,传统算法、改进算法1、改进算法2、文献[6]算法、文献[7]算法以及本文算法均随着节点通信范围的增加而有所下降,但本文算法对节点通信范围容错性较强,在较短通信范围的情况下依然可以保持良好的定位准确度,这也在一定程度上节省了传感器的通信能量开销,在保持良好定位准确度的同时,本文算法使得网络更节能. 在仿真环境边长均为100×100的正方形区域内,随机投放的节点总数变化为100,150,200,250,300,350,400,450,500,其中锚节点比例为0.3,节点通信范围为40m,每次实验结果对其取100次的均值,观察6种算法对未知节点定位的准确度. 图5 节点总数与平均误差的变化趋势图Fig.5 Trend chart of the total number of nodes and average error 从图5中可以看出,在同一仿真条件下,在节点总数为100时,本文算法相对传统算法、改进算法1、改进算法2、文献[6]与文献[7]算法的误差降低了[0.2057,0.1383,0.048,0.1357,0.0959],在节点总数为300时,本文算法相对传统算法、改进算法1、改进算法2、文献[6]与文献[7]算法的误差降低了[0.2502,0.1589,0.0647,0.1332,0.0971],在节点总数为500时,本文算法相对传统算法、改进算法1、改进算法2、文献[6]与文献[7]算法的误差降低了[0.2674,0.1657,0.0679,0.1306,0.0903],由此可以得出,本文算法对节点数量适应性较强,在较低节点总数的情况下,定位精度依然比较高,从而本文算法的实用性更强,更健壮. 从计算时间分析,在一个1.8GHZ Intel Core i7 CPU和8GB RAM的系统上进行测试,节点总数分别为100,300,500,其中锚节点比例为0.3,通信半径为50m,其中文献[7]算法的迭代数MAXG为50次,粒子数NP为30,每次时间结果取100次的均值(以秒为单位),如表1所示. 为此,从计算时长上来看,本文算法的计算量远远小于使用改进仿生算法的文献[7],与传统算法相比,本文算法计算量也仅有小量增加,从精度上来看,本文算法的误差最低,具有较好的实际应用前景. 表1 不同条件下算法的平均运行时间对比Table 1 Comparison of the average running time of the algorithm under different conditions 本文算法针对原始算法的跳数、跳距不准确性进行了相应分析与改进,并提出了对坐标三次修正的方法,针对原始算法离散跳数不准确的特点,提出基于RSSI测距的连续跳数划分概念,其次原始算法采用无偏估计的方式计算跳距,在总体误差最小化时,未能使得各项误差最小化,因此本文采用平方误差函数作为适应度函数对跳距进行求解,且原始算法未考虑到在锚节点计算跳距过程中的跳数与距离的匹配关系,跳距引入了更多的误差,为此提出跳数-距离匹配因子对各锚节点在适应度中进行加权,从而得到更精准的跳距.且由于DV-Hop算法是一种依赖网络拓扑的算法,其依靠连通性即可完成对未知节点的定位,根据此特性,提出使用新的锚节点误差反馈策略的拓扑定位误差传递的思想,对使用了优化跳数、跳距计算出的估计坐标进行第1次修正,其次本文对修正后的坐标进行泰勒展开寻优,并将展开式代入未知节点方程组中,进一步对未知节点估计坐标进行修正,最后加入场景性限制条件,第3次修正未知节点坐标.实验也表明,每一步均对未知节点的估计坐标起到了精化作用,该算法的使用使得未知节点定位更准确,且具有实用价值.在以后的工作中,将着重于对加入构建的动态锚节点对误差传递并修正的效果影响以及拓展至三维条件.3.5 算法实施步骤
4 算法分析与实验设计
4.1 锚节点比例与平均定位误差分析

4.2 通信范围与平均定位误差分析

4.3 节点总数与平均定位误差分析
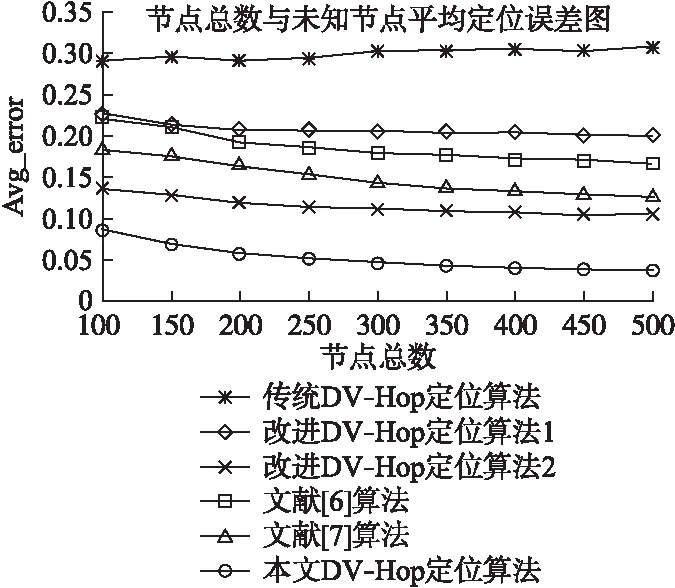
4.4 算法计算时长分析
5 结束语
