基于ARIMA-BP神经网络模型的桥梁SHM应变预测分析
2022-08-23胡琼清伍伟斌钟菊芳
邱 卓, 胡琼清, 伍伟斌, 钟菊芳, 万 灵,3
(1.江西省交通科学研究院有限公司, 南昌 330200; 2.南昌航空大学 土木建筑学院, 南昌 330063;3.浙江大学 建筑工程学院, 杭州 310058)
“十四五”以来,中国为实现交通强国,提升公路桥梁安全耐久水平,多次强调公路桥梁建设健康监测系统的必要性[1]。早在20世纪90年代初期,国家就已经开始注意到结构健康监测系统在桥梁建设、运维、养护中所起的重要作用;时至今日,桥梁健康监测系统已在国内300余座桥梁中得到广泛运用[1]。监测系统实时采集得到的监测数据,是体现桥梁结构特性的重要指标,因此对监测数据的分析及预测是评估桥梁结构状态发展趋势的重要基础[2]。
从国内外学者对桥梁监测数据预测方法研究[3-9]了解到,目前桥梁监测数据预测分析大多采用单一预测模型。如Datteo等[3]利用确定AR模型模拟了桥梁系统的结构响应特征;Oliveira等[4]基于ARIMA算法进行了桥梁结构有效损伤识别;刘启斌等[5]建立了监测数据的长短时记忆网络,实现了谐波监测数据的预测;陈兵[6]基于灰色系统理论,利用最小二乘法构建了GM(1,1)时间响应函数,并结合实际工程数据,得到了良好的预测结果;陆萍等[7]以江津长江大桥健康监测数据为例,建立了ARIMA预测模型,并针对桥梁监测系统的挠度数据进行了预测分析;沈健[8]就天津海河大桥健康监测系统,利用了BP神经网络模型在数据识别中的优势,进行多传感器与单传感器数据的对比融合分析;张鹏[9]利用基于BP神经网络模型的数据挖掘技术对桥梁监测数据进行分析,建立了监测数据的预测模型。
然而,传感设备在服役期所采集的数据往往具有波动性与随机性,采用单一的预测模型可能会存在些许误差[10]。为探究单一预测模型的误差范围,比较不同预测模型的预测效果,本文以江西省某跨江大桥SHM(structural health monitoring,结构健康监测)的实测应变数据为例,选用线性研究理论和复杂性研究理论的经典模型——ARIMA模型和BP神经网络预测模型[10],针对上述问题进行研究与对比,同时提出基于两种基础理论模型的加权预测模型与组合预测模型,并将其预测结果分别与两种基础预测理论模型进行对比,验证两类新模型的合理性与准确性。
合理地构建桥梁监测数据预测模型,能有效地对监测数据进行预警,为桥梁的维护决策提供依据的同时,还能有效地控制结构安全事故的发生,具有重大的工程意义。
1 预测理论模型
1.1 ARIMA模型
自回归积分滑动平均模型ARIMA(p,d,q)是目前应用较为广泛的时间序列模型,其实质是在自回归移动平均模型的基础上针对不平稳信号进行差分处理。ARIMA模型的主要思路为:①利用ADF单位根测试检验信号是否为平稳信号;②若信号为非平稳信号,则对其进行d阶差分以得到平稳信号;③将平稳信号通过使用自相关函数(ACF)和偏相关函数(PACF)来通过截尾性或拖尾性来判定自回归(AR)模型的阶数p和移动平均(MA)模型的阶数q,判定方法参照表1;④通过确定ARIMA模型的参数(p,d,q),就可利用预测函数对测试数据集的值进行预测。
ARIMA(p,d,q)模型的表达式为
(1)
式中:φi(i=1,2,…,p)及θi(i=1,2,…,p)分别为自相关系数和移动平均系数;φ(K)为自相关系数多项式;θ(K)为移动平均系数多项式;K为滞后算子;∇d指d阶后向差分;t为期数;Xt为时间序列;εt为第t期的残差项。

表1 阶数判定方法
1.2 BP神经网络模型
BP神经网络(back-propagation network)是一种具有误差后向传播并重训练的多层前向网络,其通常结构为输入层、隐含层及输出层。该类方法的主要思路为:将输入数据通过权重矩阵映射到隐含层,再通过权重矩阵映射到输出层,然后与期望输出相比较,若是不符合则将误差反向传播,误差以某种形式通过隐含层像输入层逐层反向传递,反反复复,直至输出满足期望输出或者达到学习次数停止,由此得到预测模型。BP神经网络算法的计算公式为
(2)
式中:xi为输入层的输入值;yk为输出层的输出值;f1及ωij分别为输入层与隐含层之间的激活函数及权值;f2及ωjk分别为隐含层与输出层之间的激活函数及权值。
2 加权预测模型
桥梁SHM应变数据通常与结构温度具有较强的相关性,而温度的变化往往具有趋势性,但应变数据却不完全受温度的影响,无论是适用于线性序列预测的ARIMA模型[12],还是适用于非线性序列预测的BP神经网络模型[13],皆无法对桥梁SHM应变数据进行精确地预测。因此,应当结合二者模型的优点,构建更为精准的预测模型。
加权预测模型是指利用ARIMA预测模型与BP神经网络模型分别对桥梁SHM实测应变序列进行拟合分析,将二者得到的预测序列进行权重分配再求和,以得到与实测应变序列误差最小的预测序列。该方法的表达式为
Jt=k1X1t+k2X2t
(3)
式中:Jt为加权模型预测序列;X1t为ARIMA模型预测序列,k1为其权值;X2t为BP神经网络预测序列,k2为其权值;k1+k2=1。
实现加权预测模型分为以下5个步骤:
第1步,确定差分阶数d。将SHM应变序列同时通过ADF和KPSS检验以判断原序列是否平稳,若序列未能通过平稳性检验,即采取差分运算直至该序列达到平稳。
第2步,将平稳信号通过使用自相关函数(ACF)和偏相关函数(PACF)识别其截尾或拖尾得到p和q(识别判定方法见表1),构造ARIMA(p,d,q)模型并得到ARIMA模型预测序列。
第3步,构建BP神经网络的结构,配置隐含层层数、最小学习率及最大训练误差。
第4步,以前10个应变数据作为输入值,将第11个数值作为输出,进行滚动训练,依据上一步所配置的各项参数不断对预测参数进行调整,直至满足误差要求或超过最大训练次数,得到BP神经网络预测模型,并利用该模型得到BP神经网络预测序列。
第5步,参照式(3)的运算规则,利用MATLAB建立一个关于k1=0.1,0.2,…,0.9的循环,求得各k1对应的加权模型预测序列,令原始序列分别减去这些加权模型预测序列,得到各k1对应误差序列,对误差序列的绝对值进行求和得到各序列的误差总和,选择较小两个误差总和对应的k1值,即判定在此区间内可以找到最小误差的权值,反复运用上述这一夹逼方法,求得权值k1与k2。
3 组合预测模型
结合实际工程经验,桥梁SHM应变数据的变化往往与其结构温度变化具有一定的相关性,而结构温度受大气温度昼夜、季节更替的影响会出现趋势性,因此导致桥梁SHM应变数据也存在变化趋势。
组合模型针对SHM应变序列具有趋势变化的特点,采用适合于线性研究理论模型的ARIMA对桥梁SHM应变序列的趋势项部分进行预测,再选用BP神经网络模型对应变序列除趋势项以外的细节项部分进行预测,最后将二者模型的预测序列进行叠加,形成组合预测序列。组合预测模型流程如图1所示。
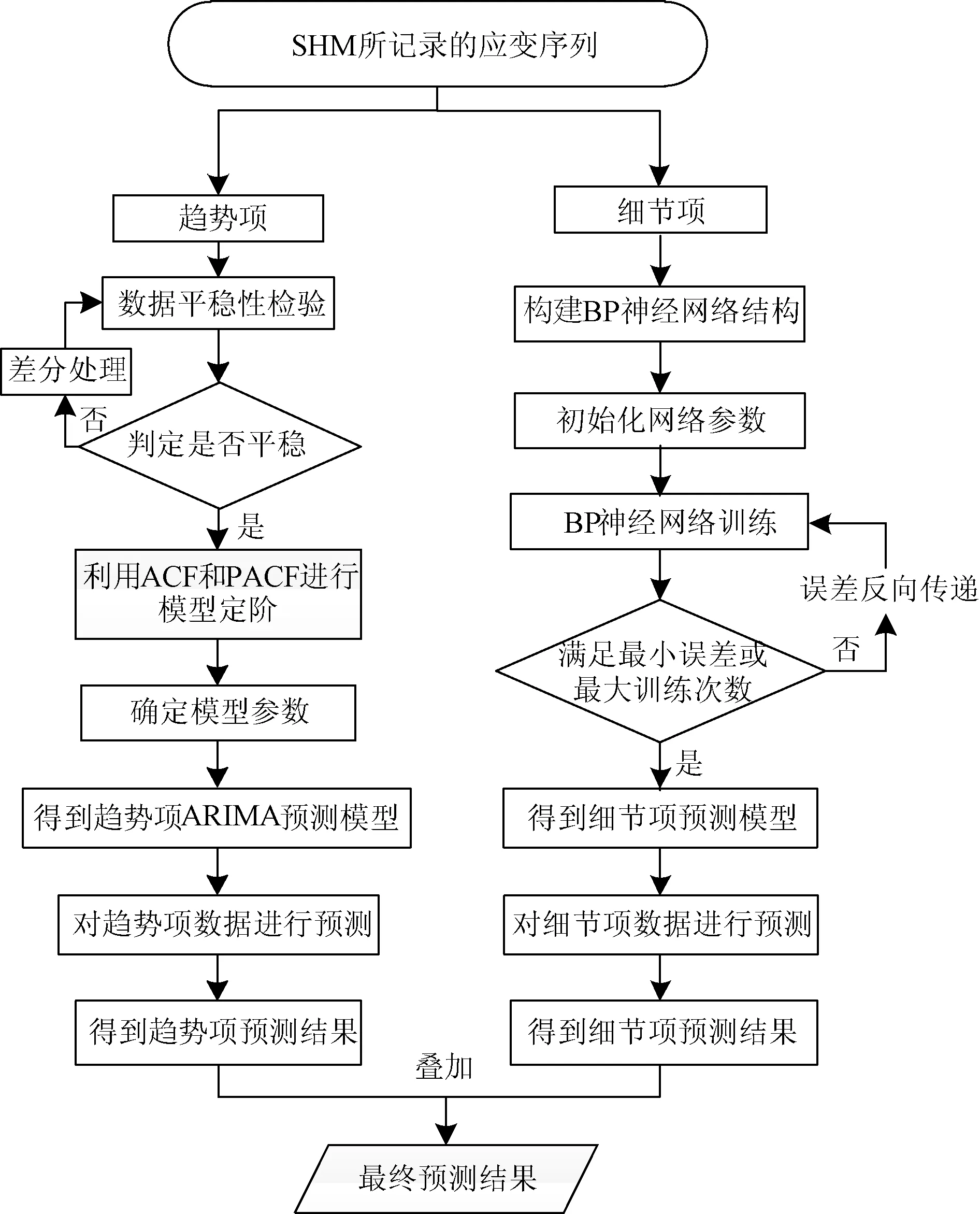
图1 组合预测模型流程
4 桥梁SHM应变数据预测
4.1 数据选取及处理
选用江西省某跨江大桥桥梁结构健康监测系统2021年4月的某一应变传感设备记录的应变监测数据作为分析案例。由于应变传感设备的采集频率较高,数据量过大,不利于分析效率,因此对所采集到的数据进行抽样提取,同时再利用3倍标准差原则对记录数据进行剔除异常值处理,最终共获取600个应变数值,用以后续的预测分析。
4.2 应变数据预测
4.2.1 单一模型预测分析及对比
利用1.1节ARIMA模型理论,对所选取的应变序列进行预测分析。经验算,ARIMA(4,1,5)的模型参数最为适用此次应变数据的预测。该模型的预测效果如图2所示。经整体观察,ARIMA预测序列基本与原应变序列贴合。为更加清晰地分辨其预测效果,特将420~540期处数据情况进行局部放大,可见ARIMA预测序列确与原序列存在细微的偏差。通过计算其误差评价得到该模型的残差平方和SSE(sum of squared error)、均方误差MSE(mean squared error)、平均绝对误差MAE(mean absolute error)、平均绝对百分比误差MAPE(mean absolute percentage error)、均方根误差RMSE(root mean square error)及决定系数R2(coefficient of determination)分别为7.332 8、1.354、0.083 4、39.28%、0.110 6、0.998 7。

图2 ARIMA模型预测结果
运用1.2节BP神经网络模型理论,对所选取的应变序列进行预测分析。神经网络模型采用3层网络结构,10个输入节点,10个中间节点和1个输出节点。设定学习率为0.1,最大训练次数为50 000,最大训练误差为0.01,建立BP神经网络预测模型,并利用该模型得到BP神经网络预测序列。该模型的预测效果如图3所示。经整体观察,BP神经网络预测模型较好地贴合了原应变序列的数据变化,经局部放大处理,可以直观地看出其预测效果与真实数据变化趋势完全一致,但依然存有部分误差。

图3 BP神经网络模型预测结果
结合图2与图3进行分析,可明显看出BP神经网络预测序列与原数据的贴合度优于ARIMA预测序列,两类模型的误差评价见表2。由表2可知,BP神经网络误差评价指标SSE、MES、MAE、MAPE、RMSE及R2分别为2.594 8、0.805、0.050、23.68%、0.065 8及0.999 5。其中,决定系数越高说明预测误差越小,其余评价指标越高预测误差越大。经分析,在此案例中,BP神经网络模型各误差评价指标均要优于ARIMA模型,因此认为,BP神经网络模型相比ARIMA模型更适用于本案例的预测分析。两类模型的误差对比如图4所示,其中ARIMA模型的误差包络范围明显大于BP神经网络模型,前者误差总和约为50 με,后者误差总和约为30 με。

表2 ARIMA、BP神经网络模型误差评价
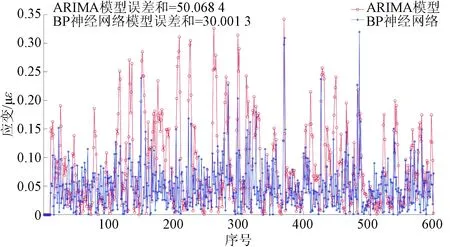
图4 ARIMA、BP神经网络预测误差对比
4.2.2 ARIMA-BP神经网络加权模型预测分析
为探究更好的预测模型用以桥梁SHM应变预测,通过结合各单一模型的优势,采用第2节提出的加权思路,对两类模型进行加权处理,以得到新的加权预测模型,并验证其合理性及有效性。其方法前4步分别为各单一模型的构建思路,第5步利用夹逼方法不断对加权预测序列的权值进行迭代,直至找到权值最优解,经反复运算,得到最终权值k1=0.332 1,k2=0.667 9,其最小误差总和为21.092 7 με。将加权系数代入至加权公式中求得最终的加权预测序列,预测效果如图5所示。由图5可见,加权模型的预测结果与原序列的贴合度明显要优于单一模型,该模型既能完美符合变化趋势的同时几乎不与原序列曲线存在预测误差。
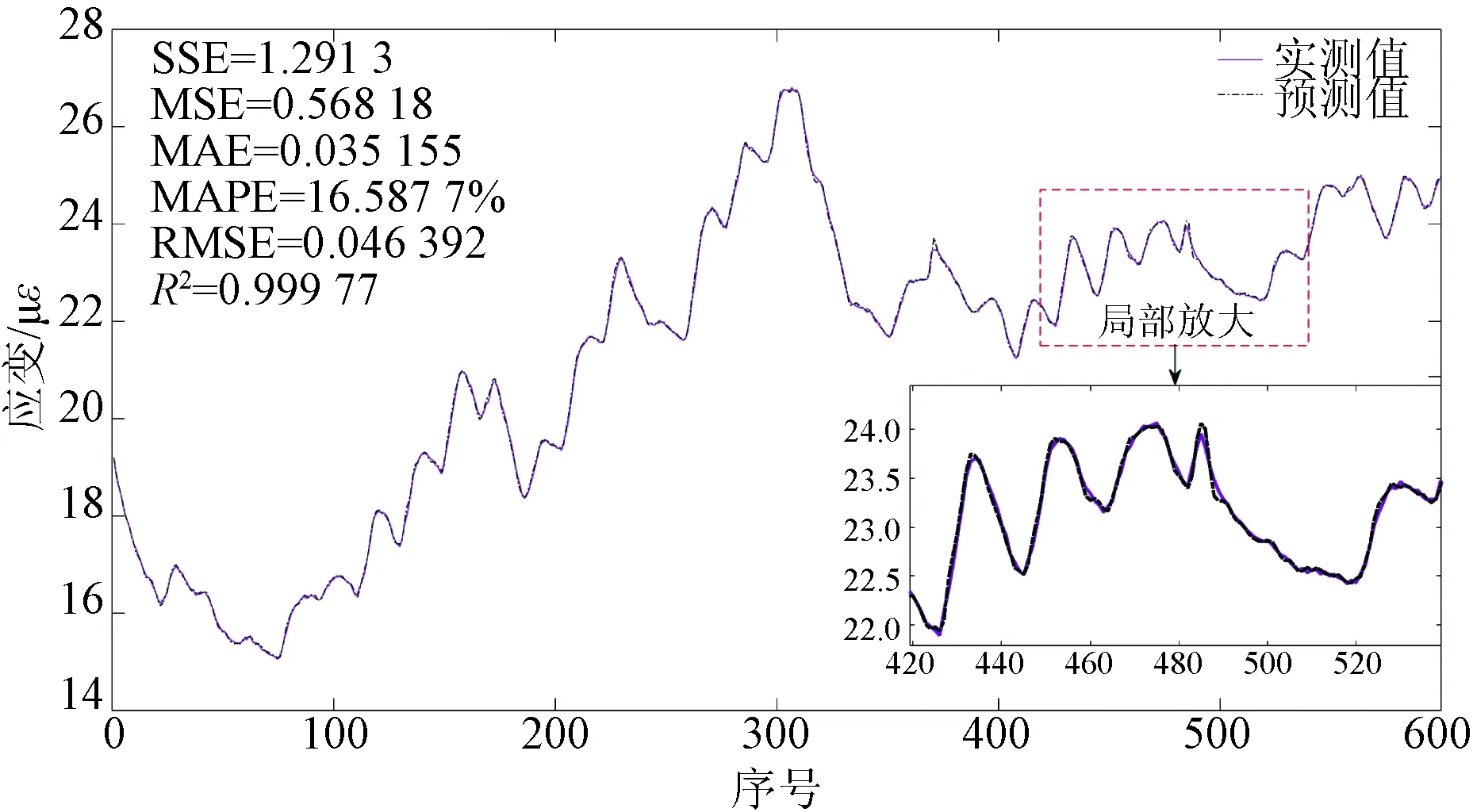
图5 ARIMA-BP加权模型预测结果
4.2.3 ARIMA-BP神经网络组合模型预测分析
由于应变数据的变化不仅具有趋势性,还具有细微波动的复杂性,于是可对应变数据进行分解,将其分解为趋势项序列与细节项序列。已有研究表明,ARIMA适用于对趋势项这一线性变化的序列预测,BP神经网络模型则更适用于细节项这一复杂的序列预测[14]。因此,可参照第3节的思路,利用ARIMA对桥梁SHM应变序列的趋势项部分进行预测,再选用BP神经网络模型对应变序列除趋势项以外的细节项部分进行预测,最后将两类单一模型进行组合叠加,以获得新的组合预测模型,并参照组合模型得出组合预测序列,预测效果如图6所示。由图6可见,组合模型的预测效果明显要优于单一模型,可以认为,该组合模型能很好地对原序列进行预测。
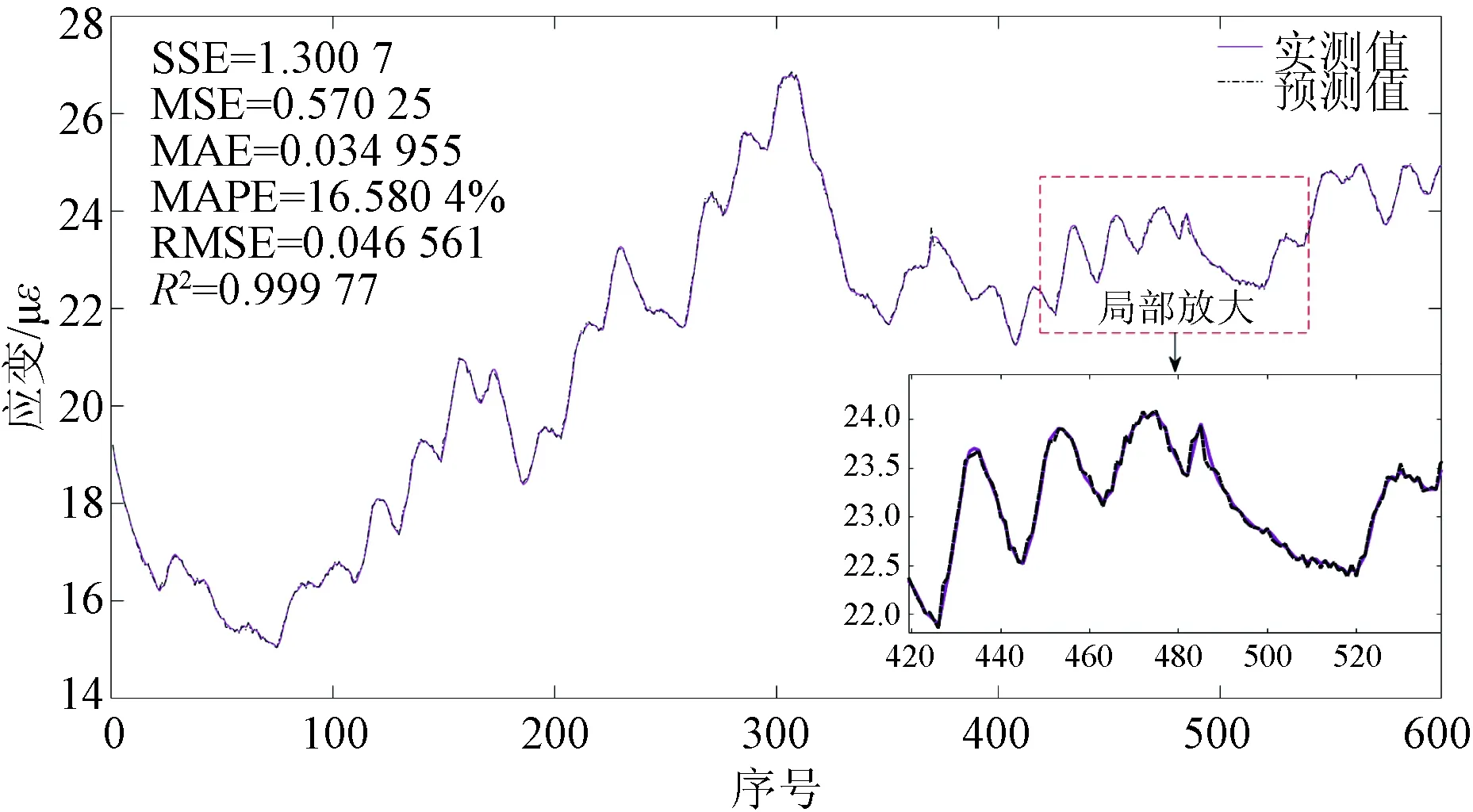
图6 ARIMA-BP组合模型预测结果
4.2.4 模型评价
由4.2.1节已知,BP神经网络预测模型的预测效果要优于ARIMA预测模型,因此将加权模型、组合模型与BP神经网络预测模型进行对比,以分析加权、组合模型的优势与合理性。各类模型的误差评价见表3。由表3可知:无论是加权模型还是组合模型的误差评价均优于单一模型,且各项指标均相差较大,其中加权与组合模型的SSE与BP神经网络模型相差最大,高达50.23%;加权模型的各项误差评价指标均与组合模型的评价指标十分接近,其中,加权模型的SSE、MES、RMSE分别比组合模型的低0.009 4、0.002 1、0.000 2,加权模型的误差指标MAE、R2与组合模型的相等,而MAPE高于组合模型0.01%。
图7及图8分别为BP神经网络与ARIMA-BP加权模型预测误差对比以及BP神经网络与ARIMA-BP组合模型预测误差对比。由图7、图8可知,BP神经网络模型的误差包络范围明显大于其他两类模型,其中加权模型的误差总和约为21.09 με,组合模型的误差总和约为20.97 με,均小于BP神经网络预测模型的误差总和。因此,在本案例中,可以认为加权模型和组合模型的预测效果均要优于单一模型。图9为ARIMA-BP加权模型与组合模型预测误差对比。分析图9,两类模型的误差包络范围接近,结合表3中的各项误差评价指标进行分析,可以认为ARIMA-BP加权模型与组合模型均适用于本案例应变序列的预测分析。
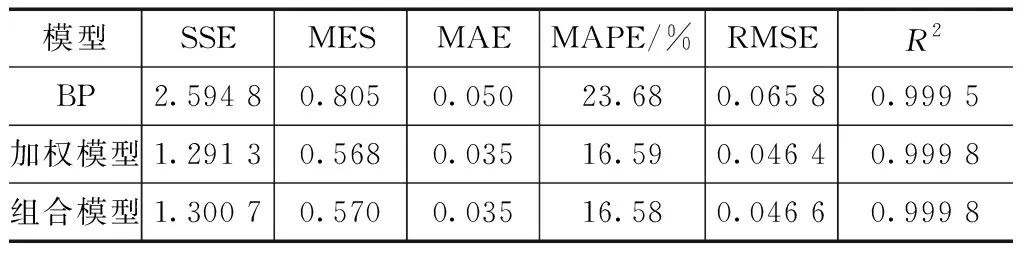
表3 不同预测模型的误差评价
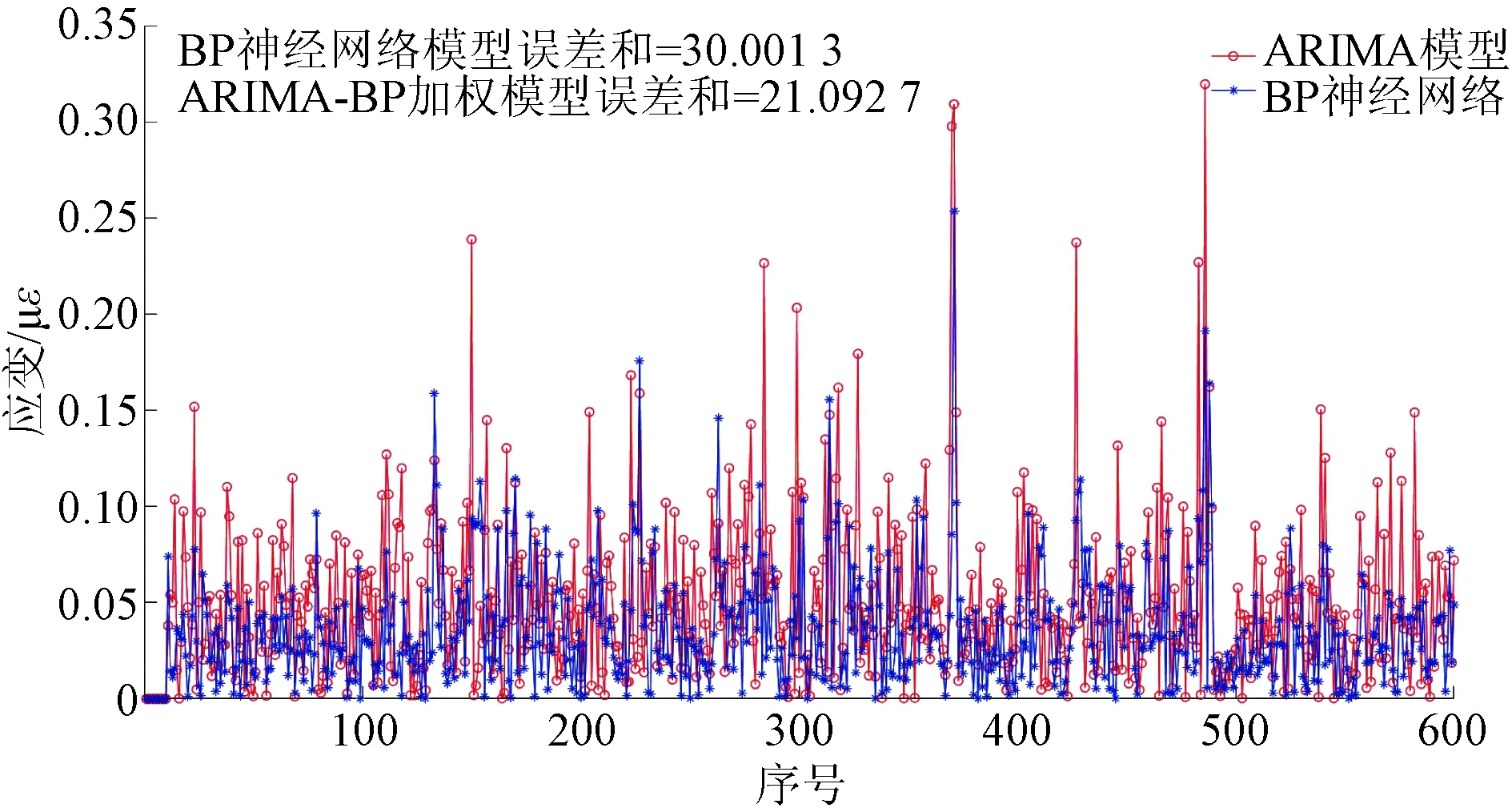
图7 BP神经网络与ARIMA-BP加权模型预测误差对比
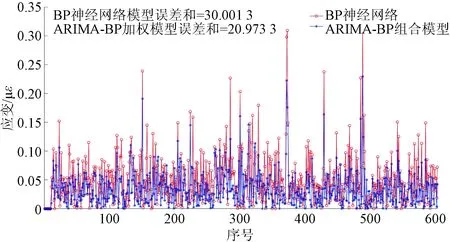
图8 BP神经网络与ARIMA-BP组合模型预测误差对比
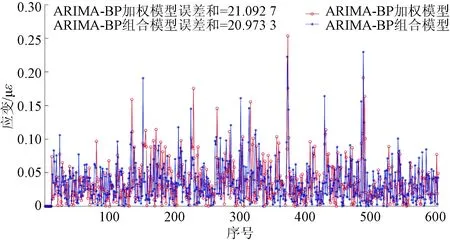
图9 ARIMA-BP加权模型与组合模型预测误差对比
5 结论
通过对ARIMA模型与BP神经网络这两个分别适用于线性研究理论和复杂性研究理论的经典模型进行梳理,提出了基于这两种预测模型的加权模型与组合模型更适用于桥梁SHM应变预测的方法。并以江西省某跨江大桥桥梁结构健康监测系统的某一应变传感设备记录的应变监测数据为例验证了两种方法的合理性。得出以下结论:
1)BP神经网络模型的预测结果优于ARIMA模型的预测结果。
2)当ARIMA-BP神经网络加权模型的权值k1取值0.332 1,k2取值0.667 9时,存在模型最小误差总和,值为21.092 7。
3)无论是预测结果还是预测的误差指标均表明,ARIMA-BP神经网络加权模型与ARIMA-BP神经网络组合模型均相比单一模型具有更好的预测效果。
