面向遥感影像分类的时延权重及群体分类PSO改进方法
2022-08-23于国强宋君陶于军令滕俊利张丽丽林琳
于国强,宋君陶*,于军令,滕俊利,张丽丽,林琳
(1.山东省圣达地理信息测绘工程有限公司,山东 威海 264200;2.山东正大地理信息科技集团有限公司,山东 潍坊 261000;3.山东省水利科学研究院,山东 济南 250014)
0 引言
遥感影像是获取地球资源与环境信息的重要手段,广泛应用于农业、林业、地质、海洋、气象、水文、军事、环保等领域。近年来,山东省大力推进数字强省建设,打造具有山东特点的一体化智能监测技术体系和常态化监测机制,这些对山东省遥感影像数据生产处理能力提出了更高要求。
遥感数据处理具有计算量大、数据密集、计算模型复杂等特点,而且近年来随着遥感数据获取终端的不断发展,遥感数据的来源更多,数据类型更加多样,数据处理模型也更为复杂。为了应对这些挑战,一些智能化算法在遥感数据处理模型解算中得到了应用,其中粒子群算法应用相对广泛[1-2]。
Kennedy与Eberhart于1995年提出了粒子群优化算法(Particle Swarm Optimization,PSO),该算法受鸟类群或鱼类群中生物运动的启发,通过模拟运动过程并进行模型构建,实现目标的优化,PSO是群体智能算法的一种[3-5]。
PSO是一种群体优化算法,其通过不断的迭代来逐步改进候选解的精度,从而实现优化的目标。PSO具有参数少、流程简单的特点,同时具有较好的鲁棒性和收敛性,应用于很多单目标优化、多目标优化问题。PSO首先设定一组初始解(即粒子),然后根据粒子位置和速度变化数学公式,在解空间中移动这些粒子,每个粒子运动受个体及群体位置的影响,在整个粒子群群体中,这些位置是逐步向最优解逼近的,当粒子群移动的次数(即迭代次数)到达一定数量时,能够获得满足精度要求的解,多数情况下,通过粒子群获得的是近似解而非准确解,并且每次计算的结果也是不一致的[6-7]。
PSO不同的参数会对优化结果产生非常大的影响,所以科学、合理的参数是PSO算法优化的重要内容。PSO是一种元启发式算法,通过很少的假设来进行问题优化,同时适用于大范围的解空间。然而PSO的初始模型在解决简单模型时能够获得理想的结果,由于基础粒子群算法步骤较为简单,当面对离散型等相对复杂的模型时,往往容易陷入局部最优解,从而无法得到理想的解结果。本文从遥感数据处理模型的特点出发,通过参数动态更新及粒子群群体分类2种策略,提出了一种基于PSO的改进算法,经过实验分析,该算法较基础粒子群算法具有明显优势。
1 相关工作
1.1 PSO算法基础
PSO算法是基于群体的,个体根据对环境的适应度,结合群体的适应度,移动到更佳的位置。粒子在解空间中以一定的速度飞行,这个速度取决于其自身飞行经验和群体中同伴的飞行经验来动态调整。粒子的飞行决定因素,如图1所示,速度的计算如公式(1)所示,位置的计算如公式(2)所示。
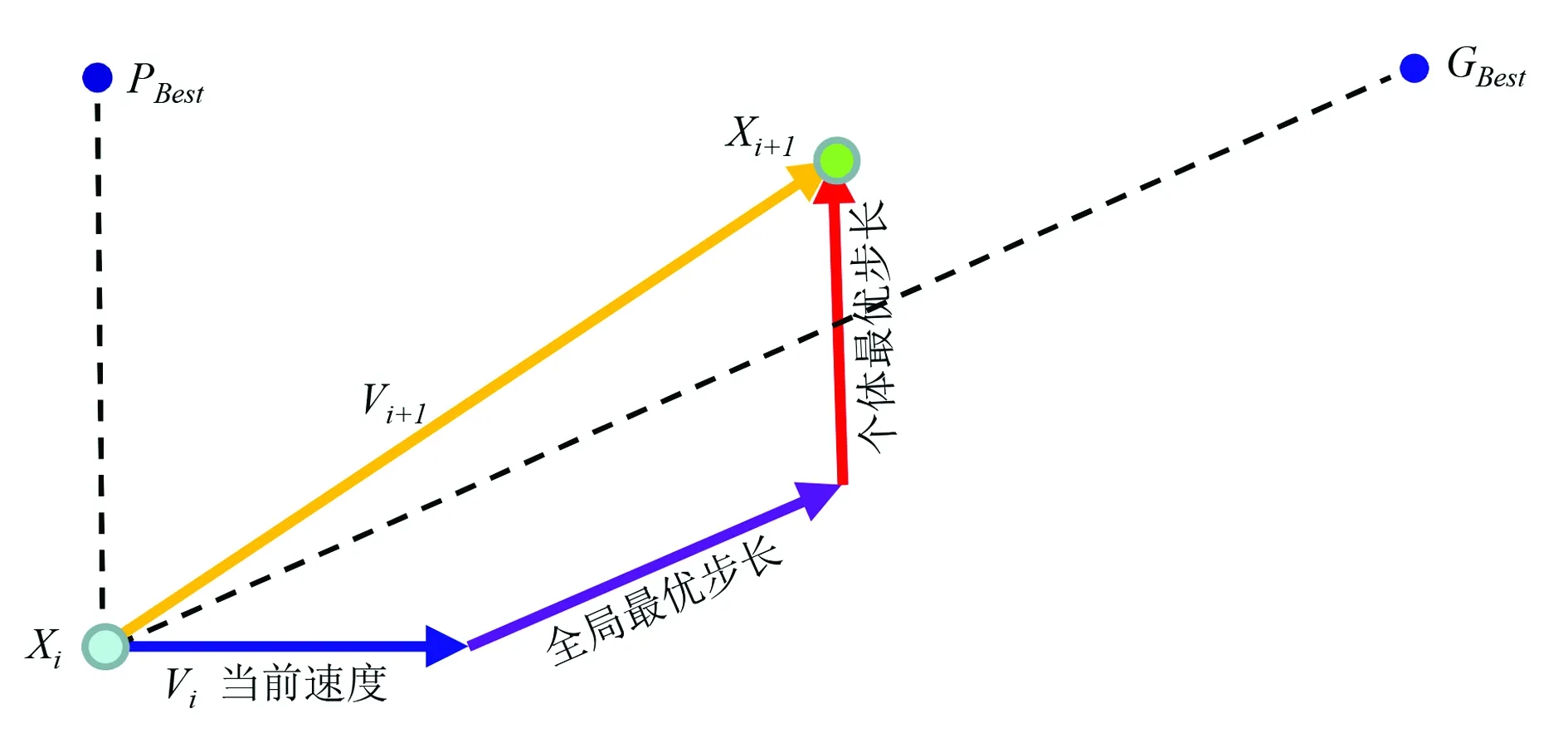
图1 粒子位置更新示意图
Vi+1=ω·Vi+c1·γ1·(PBest-Xi)+c2·
γ2·(GBest-Xi)
(1)
Xi+1=Xi+Vi+1
(2)
其中:ω为速度系数;Vi为当前速度;c1为个体最优步长系数(学习因子);γ1为随机数(范围一般为[0,1]);PBest为个体最优位置;Xi为个体当前位置;c2为全局最优步长系数(学习因子);γ2为随机数(范围一般为[0,1]);GBest为全局最优位置;Vi+1为粒子新的速度;Xi+1为粒子新的位置。
PBest、GBest通过目标函数进行判断,即将粒子的新位置代入目标函数计算新的目标函数值。
针对基础粒子群算法的问题,国内外很多学者从收敛速度、增加多样性、全局方法等方面提出了诸多改进策略,总体可以归纳为惯性权重法、模糊惯性权重法、压缩因子法、选择法、繁殖法、空间邻域法、邻域拓扑法、社会趋同法、序列生境技术法、函数延伸法等方法[8-14]。本文提出的参数动态更新及粒子群种群分类,是从收敛速度、增加多样性2个方向对PSO算法进行改进。
1.2 PSO算法在遥感中的应用
PSO算法提出后,国内外很多学者在其基础上进行了优化,并与其他智能化算法或者遥感数据处理算法结合,将其用于遥感数据处理工作。
张兵等[7]在解决混合像元分解问题时,为了解决数据噪声引起的端元提取不准确的情况,引入了PSO,并进行了改进,重新定义了速度和位置的更新策略和表示方法,降低误差对端元提取的影响,有效提高了结果精度。烟贯发等[15]基于改进PSO优化LSSVM参数提出了一种悬浮物的遥感反演方法。为解决传统SVM分类方法的缺陷,丁胜等[16]基于PSO提出了PSO-BSSVM分类模型,大幅提高了分类精度。AN等[17]提出了一种改进的具有互信息相似性度量PSO模板匹配算法,该方法具有良好的鲁棒性,在准确性和效率方面均优于标准粒子群算法。WANG等[18]基于PSO和CNN提出了一种新的边缘检测方法,与Sobel算子和LOG算子相比,该方法取得了较好的检测效果,且结果更完整、准确。在利用PSO进行多光谱遥感影像分类时,为解决PSO容易陷入局部最优解的问题,LI等[19]提出了改进算法,该算法具有均衡的利用和探索能力,获得了更好、更稳定的分类结果。Agrawal[20]基于多目标PSO算法提出了一种最优神经网络拓扑结构自适应多光谱卫星图像分类方法,该方法比传统方法具有更大的优越性。
PSO具有简单易用、可调参数少的优点,虽然存在易提前收敛、陷入局部最优解问题,但是经过算法改进,在遥感数据处理领域得到了广泛的应用。自PSO算法提出以来,一直得到研究人员、技术人员的关注,随着人工智能算法、遥感技术的发展,经过改进的PSO算法的应用将更为广泛。
2 计算法
2.1 算法流程
为了解决标准PSO算法容易出现局部最优解,导致解不稳定,难以满足遥感数据分类需要的问题。本文从粒子群群体多样性及动态速度更新2个方向对PSO算法进行了改进。图2为本文提出改进方法的算法流程图。

图2 算法流程图
Step1:对粒子种群进行初始化,确定粒子的群体类别,即正常粒子或个体粒子,如正常粒子执行Step2,个体粒子执行Step5;
Step2:对于正常粒子,按照解空间范围,对粒子的速度、位置进行随机初始化;
Step3:基于目标函数,粒子当前位置计算粒子的适应度值;
Step4:判断当前适应度值是否是个体最优,如是则更新个体最优位置、最优适应度值,否则不更新;
Step5:对于个体粒子,首先按照解空间范围,对粒子速度、位置进行随机初始化,并计算适应度值;
Step6:个体粒子不考虑全局最优步长,仅通过个体速度和个体最优步长,来寻找新的个体位置,并利用目标函数计算新的适应度值;
Step7:获得个体粒子的个体最优位置、个体最优适应度值;
Step8:基于本轮迭代Step4、Step7的所有粒子的个体最优值,更新全局最优值;
Step9:根据迭代条件,判断迭代是否结束,如满足则结束,否则正常粒子执行Step10,个体粒子执行Step12;
Step10:对于正常粒子选择一定比例进行变异,如变异则执行Step2,未变异执行Step11;
Step11:按照速度、位置计算公式,即公式(1)、公式(2),基于Step4、Step8的结果,更新粒子个体速度及位置,执行Step3;
Step12:对于个体粒子,判断当前值是否已经满足极值条件,如满足则执行Step5,否则更新个体速度及位置并执行Step6。
2.2 改进策略
基础粒子群在解决复杂离散型问题时,最容易出现的问题是产生局部最优解,以及早熟、提前收敛等问题,避免这些问题最直接的方法是增加粒子的数量来应对陷入局部最优问题,增加迭代次数来应对解的精度问题。但是这种方法带来的最大问题是粒子群优化算法时间复杂度过高,计算量和计算时长大幅增长。
基础粒子群算法,在迭代的后期,粒子个体对最优解提升的贡献值越来越低,而且存在多数粒子工作叠加的情况,这就造成了一些粒子在做无用功。在迭代的后期,粒子数量对整体问题的性价比越来越低。因此,本文的改进策略包括优化迭代后期粒子的作用,此外为了避免陷入局部最优,增加粒子群的种群类别,通过不同种群不同分工,将粒子工作的侧重点进行区分,在不损失解精度的前提下,增加粒子在解空间分布的离散度,从而降低陷入局部最优解的风险。
将粒子分为3类,如图3所示,包括正常种群、个体种群2个大类。正常种群的粒子采用传统粒子群算法进行速度和位置更新,其中在正常种群中又存在变异粒子。个体种群粒子仅考虑个体因素进行速度和位置更新,个体种群会与全体粒子共享最优位置及最优解信息。

1—个体粒子;2—正常粒子;3—变异粒子图3 粒子群种群划分策略
个体种群粒子数量占全体粒子数量比例根据待解问题的不同,比例设定在50%~70%范围内,个体粒子仅通过个体速度及个体历史最优位置来更新当前速度和位置,但是需要对全局粒子进行信息输出,即提供个体最优解信息。当个体粒子满足最优解极值判断条件后,该粒子重新进行随机初始化,然后根据新的位置重新寻找个体最优解。
变异粒子是正常粒子在迭代过程中的变异,粒子变异后,需要重新初始化,变异粒子根据新的速度和位置进行正常更新,根本上变异粒子是正常粒子的一种,与正常粒子是可以相互转换的。为了避免一些优秀的粒子(比如当前最优位置的个体)也参与变异,从而降低求解收敛的速度及损失当前区域最优解空间,曾经获得过全局最优解的粒子均不参与变异,一直以正常粒子的身份更新。随着迭代次数的增加,变异粒子数量的比例也会越来越高,这就规避了上文提到的在迭代后期粒子群的数量,对于求解性价比不高的问题。
采用粒子群分类策略,会减少正常粒子的数量,势必影响解收敛的速度和解的精度,虽然可以通过增加迭代次数来解决这个问题,但是会相应的增加计算量,从而增加任务的时间成本。为了解决该问题,提出了时延权重动态变化的速度更新策略,该策略不但能够解决粒子群分类造成的问题,还可在迭代后期减少速度步长,从而提高解的精度。
粒子速度时延权重公示如公式(3)所示。
(3)
其中:WV为粒子速度的权重;Ic为当前迭代的次数;Iall为迭代总次数;qv为权重系数。
从公式(3)可以看出,随着迭代次数的增加,粒子速度时延权重值越来越小,在计算粒子速度时,个体速度的影响力也越来越小,此外个体整体速度也会越来越小,这样就降低了速度的步长,利于迭代后期解精度的提高。
为了改变不同迭代阶段个体最优步长及全局最优步长对解收敛速度及解精度的影响,本文对基础粒子群算法中的个体最优步长系数、全局最优步长系数,即公式(1)中的c1、c2,进行了动态调整。c2时延权重计算如公式(4)所示,时延权重计算如公式(5)所示。
(4)
Wc2=1-Wc1
(5)
改进后,粒子速度的计算如公式(6)所示,即公式(1)的改进。
Vi+1=WV·ω·Vi+Wc1·c1·γ1·(PBest-Xi)+Wc2·c2·γ2·(GBest-Xi)
(6)
3 实验及结果分析
基于提出的时延权重及群体分类PSO改进方法,对遥感数据分类进行实验,经实验结果分析,取得了较为理想的分类结果。为了精确验证算法的改进效果,以严格的数学函数模型作为目标函数,来对最优解进行量化分析。
目标函数如公式(7)所示,该函数存在多个凸凹区域,容易陷入局部最优解,如图4所示。实验采用的参数设置如表1所示。
f(x,y)=20+x2+y2-10·cos(2·π·x)
-10·cos(2·π·y)
(7)
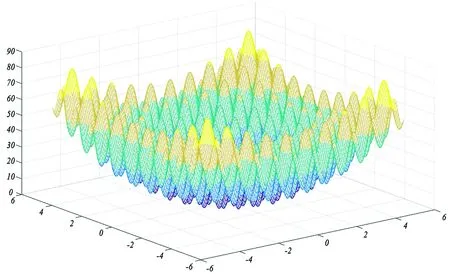
图4 目标函数示意图

表1 参数值设置
将粒子个数分别设定为30、60、90个,迭代次数分别设定为20、40、60、80次,粒子群体正常粒子的比例为60%,个体粒子的比例为40%,正常粒子的变异比例随着迭代次数的增加而提高,如公式(8)所示,qm取值0.7。
(8)
实验对不同粒子数量及不同迭代次数进行了组合,并分别进行了10000次实验,提出的改进算法与基础算法进行了对比和分析。表2所示,其中带有星号(*)的数字为本次提出方法的结果。图5通过100×100像素的图像展示了不同实验方案的结果及趋势,彩色点为局部最优解及解精度大于0.05的情况。

表2 实验结果统计
通过表2、图5可以看出,本文提出的方法相对基础粒子群算法具有明显优势,在陷入局部最优解的次数上,明显少于基础算法,相应精度上也有所提升。通过表2可以看出,在粒子数60的情况下,本次改进的优势最为明显,随着粒子数及迭代次数的增加,算法的优势有所降低,但是相对基础算法,仍具有明显优势。对运行效率也进行了统计,本次提出的算法虽然相对基础算法要复杂,但是运算时间没有明显增加,基本可以忽略不计。

图5 实验结果对比及趋势示意图
4 结论
从遥感影像分类需求出发,选择PSO算法为计算模型,为了解决基础PSO算法容易陷入局部最优解的情况,提出了一种新的参数动态更新及群体分类双策略改进算法。该算法在遥感影像分类中取得了理想的处理结果,同时对该算法进行了定量分析,实验结果相对基础PSO算法,优势明显。该算法通过增加粒子种群分类及粒子变异策略,增加了粒子的多样性,丰富了不同粒子的分工,不同种群粒子在寻找更高精度解或避免陷入局部最优解方面各有侧重,有效降低陷入局部最优解的比例。此外,算法引入了时延权重,改善了迭代计算后期,粒子数量对目标求解的贡献逐步降低问题,激发了粒子活力,进一步降低了局部最优解的比例。改进的算法在少量粒子个数及少量迭代次数的情况下,能够取得较为理想的目标解,适用于遥感数据处理计算量大的场景,具有较好的推广价值。
