基于多源信息融合的磁浮列车组合式测速定位方法*

成 庶 刘 畅 宋丽伟 向超群 李 林

(1.中南大学交通运输工程学院， 410075， 长沙； 2.中车株洲电力机车有限公司， 412001， 株洲∥第一作者， 教授)

区别于普通的轮轨式列车，磁浮列车与轨道间为无接触式运行，故无法通过计轴设备来进行测速定位。当前的磁浮列车测速定位方法按位置信息的参照可分为相对定位法和绝对定位法[1](见图1)。基于列车初始位置和实时位移来推算列车实时相对位置的方法称为相对定位法，其主要采用感应回线、计数轨枕、长定子齿槽检测、多普勒雷达[2]和INS(惯性导航系统)[3]等技术设备。通过轨旁装置来获取列车绝对位置的方法称为绝对定位法，其主要采用GNSS(全球卫星导航系统)[4]、查询-应答器和脉宽编码等技术。

图1 磁浮列车常用测速定位方法Fig.1 Common positioning and speed measuringmethod of maglev train

磁浮列车测速定位系统的精度和可靠性直接关系到列车的运行安全。传感器精度是测速定位系统的关键参数，受限于制造工艺和经济效益之间的平衡性，存在单一传感器应用的局限性。本文提出多源测速定位信息融合的技术[5-6]。该技术通过融合多种设备的测速定位信息，能有效实现各方法之间的优势互补，克服单一测速定位方式所造成的性能缺陷，从而大幅提高测速定位系统的精度、可靠性和抗干扰能力。

基于多源测速定位信息融合技术，本文提出一种新型的磁浮列车组合式测速定位方法，通过联邦卡尔曼滤波算法，实现INS、GNSS及多普勒雷达的三源测速定位信息的有机融合，进而实现磁浮列车的高精度实时测速和连续定位功能。

1 组合式测速定位系统的构成及原理

组合式测速定位系统的硬件包含测速定位、数据通信、数据存储和信息处理四个模块，见图2。其中，测速定位模块和数据处理模块是核心功能模块。

图2 组合式测速定位系统结构组成Fig.2 Structure composition of positioning and speedmeasuring system

1.1 测速定位模块结构组成

测速定位模块采用组合式结构，包含INS、多普勒雷达和GNSS三类信号采集终端。

INS在假设物体做匀速运动的前提下，用物力(被测对象的加速度积分变换)实现列车的测速定位。本研究选用无需稳定平台，适于装备轻量化的联捷式惯性导航技术，其不依赖于外界信息、具备完全自主导航能力，但存在积累误差的问题。

GNSS主要包含组网卫星、信号接收端和地面监控系统三部分，其测速定位性能不受限于时空及方位等因素，具有极高的测量效率和精度。为克服INS存在积累误差的缺陷，本研究选用中国北斗卫星导航系统为列车提供全天候的实时速度和位置信息，以消除积累误差。但GNSS的功效仍受限于铁路沿线如隧道等特殊封闭式地形的影响，存在卫星信号盲区等不可控因素。

针对GNSS存在信号盲区的问题，本研究采用车载XS-IQ2型测速雷达(其测速范围为0.1～2 000.0 km/h)对列车进行不间断的信息采集，成功克服了GNSS存在工作盲区的缺陷。相应的，GNSS和INS也为多普勒雷达的车体震动误差修正提供了良好参照。可见，各方法之间实现了优势互补。

由上述分析可知，这种以“核心优势”补偿“潜在缺陷”的组合方式一方面可以提高测速定位系统的整体综合效能，另一方面还为测速定位系统故障情况下的安全冗余提供了前提。

1.2 信息采集与处理

磁浮列车测速定位系统的软件功能主要包括信息采集和信息处理。通过多源测速定位模块采集的原始速度及位置信息一般可能存在互斥性，并包含各异的噪声。因此，有必要通过融合算法来对原始速度及位置等信息进行科学处理。信息采集初始化与融合信息处理的算法流程如图3所示。

图3 信息采集初始化与融合信息处理的算法流程Fig.3 Process of information acquisition initiation andfusion information treatment algorithm

2 信息融合算法

2.1 基于卡尔曼滤波的测速定位方法

通过在时域内建立测速定位系统的状态方程和测量方程，进而估算出状态变量的最优解。先以组合式测速定位系统中的某单一传感器模块为对象，本文选取位置信息S(k)和列车速度v(k)为状态变量，建立一般状态方程和测量方程如式(1)、(2)所示(其他传感器同理)：

X(k)=Φ(k,k-1)X(k-1)+

ΓW(k-1)

(1)

Zi(k)=HiX(k)+Mi(k)

(2)

式中：

X(k)——k时刻磁浮列车的状态矩阵；

Γ——测速定位系统噪声移动矩阵；

Φ(k,k-1)——状态一步转移矩阵；

W(k-1)——k-1时刻的系统噪声向量;

Zi(k)——第i类传感器的测量输出向量；

Hi——第i类传感器测量矩阵；

Mi——第i类传感器的测量噪声向量。

定义i=n、b、r，其中，n、b、r分别对应INS、GNSS和车载多普勒雷达系统。选取S(k)和v(k)为测量输出量。R(k)表示测量噪声协方差，Q(k)表示测速定位系统噪声协方差(做如下合理假设：R(k)为正定矩阵，Q(k)为非负定矩阵)。在不受线路环境影响的理想情况下，将测速定位系统噪声和测量噪声视为均值为零的高斯白噪声。由此可得卡尔曼滤波递推算法。其中，时间更新方程为：

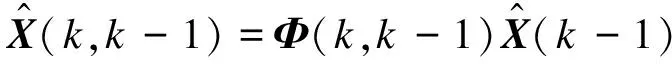
(3)

P(k,k-1)=Φ(k,k-1)P(k-1)ΦT(k,k-1)+

ΓQ(k-1)ΓT

(4)

测量更新方程为：

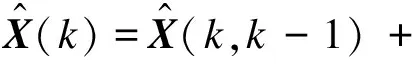
(5)

K(k)=P(k,k-1)HT·

(6)

P(k)=(I-K(k)H)P(k,k-1)

(7)

式中：

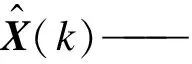
K(k)——卡尔曼滤波增益矩阵；

P(k)和P(k-1)——分别为k时刻和k的前一时刻的估计误差方差阵；

H——传感器测量矩阵；

I——单位矩阵；

Z(k)——k时刻的传感器测量向量。

2.2 组合式测速定位系统的三源融合算法

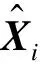
图4 三源信息融合算法框图Fig.4 Framework of three-source informationfusion algorithm

2.3 算法参数改良及可靠性优化

主滤波器会按照权重分配的优化原理将全局估计值逐一反馈到各子滤波器，用于指导各子滤波器的数据优化。分配规则如下：

其中，βi为分配系数，i=n,b,r。分配原则如下：

βr=1-βb-βn

在列车低速运行(v≤50 km/h)阶段，由于GNSS和多普勒雷达传感器的测速定位精度较低，INS有良好的表现，故βn取值较高，βb及βr取值较低。在列车高速运行阶段，GNSS误差影响降低，且多普勒雷达可更好地发挥其测速定位优势，故增大其对应的分配系数。这种考虑列车不同运行速度区间的权重调整方案可进一步提升组合式测速定位系统的精度。

此外，本组合式测速定位系统还具备安全冗余的功能。在某个传感器突发故障的情况下，可将故障模块的分配系数平均调整给其它同级子模块，以实现故障容错。同时，可借助卡尔曼滤波算法对测速定位系统状态做出可靠估计，从而实现安全过渡，在保证列车运行安全的前提下提高线路的综合运营效率。

式中：

Pj——j时刻的状态估计误差方差矩阵；

Φk,j——从j时刻到k时刻的列车状态转移矩阵;

3 磁浮列车运动模型搭建

为便于分析，可将磁浮列车视作1个处于匀速或匀加速运动状态下的惯性体。由于列车运行加速度不可突变，故列车的瞬时加速度为1个定值。此外，匀速运动模型可等效为加速度均值为零的匀加速运动模型。由此，本文最终选用匀加速运动模型来描述磁浮列车的运动状态。数学模型推导如下：

式中：

S(k)、a(k)、v(k)——分别代表k时刻的位移、加速度和速度信息；

ωS(k)、ωa(k)、ωv(k)——分别代表位移、加速度和速度信息在k时刻所包含的系统噪声。

令：

可得式(1)、式(2)所对应的列车离散状态方程和传感器测量方程如下：

代入预设参数值后，即可得到列车匀加速运行工况下的离散状态方程和传感器测量方程。

4 仿真试验

依据已建立的磁浮列车匀加速运动模型，本文借助MATLAB软件平台对本算法进行仿真试验。试验中加入的噪声参数取值如表1所示，设定仿真时长为500 s，主滤波器融合周期为1 s，则通过磁浮列车匀加速运动模型的模拟仿真，即可得到列车运行仿真结果如图5及图6所示。

表1 组合式测速定位系统的噪声参数取值表

a) 磁浮列车的速度仿真曲线

b) 局部放大图图5 速度曲线仿真结果Fig.5 Simulation results of speed curve

图5为磁浮列车的速度仿真曲线。由图5可见，融合波形与参考波形高度拟合。由局部放大图可以看出，测速误差小于±0.5 km/h。

图6为匀加速工况下磁浮列车的位置曲线及局部放大仿真结果。由图6 b)局部放大图可以看出，定位误差小于±10 m，仅在变速时刻产生较明显误差，但组合式测速定位系统仍能在短时间内恢复列车位置跟踪。

a) 磁浮列车的位置仿真曲线

b) 局部放大图图6 位置曲线仿真结果Fig.6 Simulation results of position curve

由仿真结果可知，本文提出的磁浮列车新型组合式测速定位方法能达到较高的精度水平。组合式测速定位系统在综合考虑外界干扰的情况下，仍能保持较高的校正精度和稳定的波形输出。这体现出本测速定位方案具有较优的测量精度，以及较强的鲁棒性和自主运行能力。

5 结语

本文首先分析INS、GNSS及多普勒测速雷达传感器等测速定位方法的优缺点，提出了基于多源信息融合的组合式磁浮列车在线测速定位方法；随后，基于联邦卡尔曼滤波算法，通过分配系数优化、安全冗余和状态预估等手段提高系统的测速定位精度和系统鲁棒性；然后，搭建磁浮列车匀加速运行工况下的精确数学运动模型；最后，采用MATLAB软件进行仿真试验，验证了所提方法的有效性和可靠性。