SBOOSP for Massive Devices in 5G WSNs Using Conformable Chaotic Maps

Chandrashekhar Meshram,Agbotiname Lucky Imoize,Sajjad Shaukat Jamal,Amer Aljaedi and Adel R.Alharbi

1Department of Post Graduate Studies and Research in Mathematics,Jayawanti Haksar Government Post-Graduation College,College of Chhindwara University,Betul,460001,M.P.,India

2Department of Electrical and Electronics Engineering,Faculty of Engineering,University of Lagos,Akoka,100213,Lagos,Nigeria

3Department of Electrical Engineering and Information Technology,Institute of Digital Communication,Ruhr University,44801,Bochum,Germany

4Department of Mathematics,College of Science,King Khalid University,Abha,Saudi Arabia

5College of Computing and Information Technology,University of Tabuk,Tabuk 71491,Saudi Arabia

Abstract:The commercialization of the fifth-generation(5G)wireless network has begun.Massive devices are being integrated into 5G-enabled wireless sensor networks(5G WSNs)to deliver a variety of valuable services to network users.However,there are rising fears that 5G WSNs will expose sensitive user data to new security vulnerabilities.For secure end-to-end communication,key agreement and user authentication have been proposed.However, when billions of massive devices are networked to collect and analyze complex user data, more stringent security approaches are required.Data integrity, nonrepudiation, and authentication necessitate special-purpose subtree-based signature mechanisms that are pretty difficult to create in practice.To address this issue,this work provides an efficient,provably secure,lightweight subtreebased online/offline signature procedure(SBOOSP)and its aggregation(Agg-SBOOSP)for massive devices in 5G WSNs using conformable chaotic maps.The SBOOSP enables multi-time offline storage access while reducing processing time.As a result, the signer can utilize the pre-stored offline information in polynomial time.This feature distinguishes our presented SBOOSP from previous online/offline-signing procedures that only allow for one signature.Furthermore, the new procedure supports a secret key during the pre-registration process, but no secret key is necessary during the offline stage.The suggested SBOOSP is secure in the logic of unforgeability on the chosen message attack in the random oracle.Additionally, SBOOSP and Agg-SBOOSP had the lowest computing costs compared to other contending schemes.Overall, the suggested SBOOSP outperforms several preliminary security schemes in terms of performance and computational overhead.

Keywords: Subtree-based online/offline signature procedure (SBOOSP); 5G WSNs;provably secure scheme;massive devices;conformable chaotic maps

1 Introduction

Massive access configuration enables the sharing of radio spectrum amongst an enormous number of devices.Massive access presents a potential risk of information leakage because one device in the network setting can receive a signal from other devices in the network.In order to address this access security problem, upper layer encryption techniques have been deployed[1].However, wireless communication technology is fast evolving, and eavesdropping nodes are gaining significant intrusion capabilities.As a result, the traditional encryption techniques need to be significantly enhanced to guarantee the security of user information.In recent times, massive devices are gaining widespread adoption in 5G and beyond 5G wireless communications.Massive devices are designed using cost-effective nodes,and they have limited computational processing power.Therefore, they are not able to satisfy the high complexity requirements of advanced encryption techniques.

The commercialization of fifth-generation(5G)wireless networks has facilitated advanced technologies to address the proliferating issues in 4G LTE wireless networks [2].In recent times, 5G wireless networks have witnessed the massive deployment of radio access networks to support several applications,including wireless sensor networks(WSNs)[3,4].Practically,sensor nodes in WSNs can be configured and integrated into billions of massive machine-type communication (MTC) devices(MD)in 5G wireless networks to facilitate user data transmission over WSN-assisted channels[5–7].However,there are growing concerns that the security of these channels is grossly limited,and the need to secure sensitive user data being transmitted over these channels is not negotiable[8].Toward this end,efficient,provably secure,and lightweight subtree-based online/offline signature procedures are currently being exploited to address this problem.

1.1 Motivation and Contribution

This paper presents a comprehensive overview of efficient,provably secure,lightweight subtreebased online/offline signature procedures.Most schemes are designed based on hard problems that are relatively difficult to solve in practice from the literature review.Such schemes require high computing resources and prohibitive communication costs.Moreover, most of these schemes cannot be tested entirely using AVISPA,Scyther,and other security validation tools.Therefore,deploying such schemes in small devices with limited computational resources can be detrimental and pose serious reliability issues.In order to address this problem, the need to exploit efficient, provably secure, lightweight subtree-based online/offline signature procedure (SBOOSP) to boost the security and extends the processing capabilities of resource-limited massive devices in 5G WSNs is not out of place.Thus,we present an efficient,provably secure,lightweight subtree-based online/offline signature procedure(SBOOSP)for massive devices in 5G WSNs.It is worth mentioning that the proposed SBOOSP lowers the computational and communications costs drastically.

Additionally, the current study is motivated by using conformable chaotic maps to design the SBOOSP scheme for application in massive devices in 5G WSNs.The proposed SBOOSP demonstrates appreciable security in random oracle unforgeability of subtree-based signature(STBS)under chosen message attack.Furthermore,we present an extension to the proposed SBOOSP to facilitate the registration and implementation of different messages in 5G WSNs.Additionally, our SBOOSP was tested and compared with several schemes using standard metrics.Finally, our SBOOSP offers robust and superior security characteristics to the preliminary schemes applied to resource-limited and low-powered devices in 5G WSNs.

1.2 Paper Organization

The rest of this work is arranged in the following manner.Section 2 gives a brief literature review.Section 3 presents the preliminary background to conformable chaotic maps and notations associated with subtree.Section 4 offers the proposed efficient,provably secure,lightweight subtreebased online/offline signature procedure for massive devices in 5G WSNs using conformable chaotic maps.In Section 5,the security examinations and helpful discussions are reported.The aggregation of the proposed SBOOSP scheme for massive devices in 5G WSNs is highlighted in Section 6.Section 7 discusses the performance analysis of SBOOSP and Agg-SBOOSP.The primary setting of the SBOOSP technique for massive devices in 5G WSNs is presented in Section 8.Finally, a concise conclusion to the paper is specified in Section 9.

2 Related Works

The traditional encryption schemes depend on secure key distribution that may not find practical applications in massive devices such as grant-free random access in 5G and beyond 5G wireless networks.Thus,there is a need to deploy physical layer security schemes to complement the conventional encryption schemes to guarantee secured massive access in 5G WSNs[9].The physical layer security ensures that the eavesdropping channel capacity is less than the information transmission percentage of the link being considered.Consequently, it becomes challenging for the eavesdropper to decode the intercepted signal accurately [10,11].In order to improve the secrecy performance of physical layer security, there is a need to degrade the quality of the eavesdropping signal while enhancing the quality of the desired signal significantly.Thus, multiple-antenna schemes have been employed to provide physical-layer security [12].By transmitting the desired signal in the null space of the eavesdropping channel matrix,it becomes extremely difficult for the legitimate signal to be intercepted by the eavesdropper[13,14].However,the high spatial resolution of large-scale antenna arrays in 5G wireless networks can be exploited to guarantee secure access for massive devices in 5G WSNs[15,16].

In the existing literature, Even et al.[17] proposed online/offline signature to address some of the highlighted security vulnerability issues.Part of the signature process is carried out online, and the other part was done offline.The offline-signing process consumes considerable time and is more costly in terms of computational resources.Additionally, the online signing phase is much faster,lightweight,and efficient.In Even et al.[17],a general construction suitable for transforming a digital signature technique to its online/offline signature equivalent is presented.One major limitation of this generalized construction is the extension of each signature in a quadratic time.Interestingly,Shamir et al.[18] address this fundamental limitation using the hash-sign-switch scheme that converts any signature type.Also, some special purpose schemes have been proposed [19] to enhance the Shamir and Tauman scheme.

Kurosawa et al.[20], proposed online/offline signature procedures independent of the random oracle.Additionally,short signatures[21]and efficient online/offline schemes[22]without the random oracle have been proposed.For low-power devices,the online/offline signature procedures reported in[23]are prospective.Also,lattice-based online/offline signature procedures are given in[24].Furthermore, Xu et al.[25] presented an identity-based online/offline multi-purpose signatures procedure.Though the scheme found practical applications in IoTs and WSNs, several limitations have been reported.Li et al.[26] noticed that the scheme [25] could not restrain forgery attacks.However,recent studies have shown that Li et al.’s scheme is not entirely free from security flaws.Several security schemes reported in the literature have demonstrated various limitations requiring massive improvements.In order to address this problem, chaotic maps assisted schemes are currently being deployed to secure 5G wireless communication channels[27].These schemes have been widely applied to hash functions [28], symmetric encryption [29], S-boxes [30], and provably secure online/offline identity-based signature techniques[31].

Chain et al.[32],proposed a chaotic map-based digital signature scheme.Similarly,chaotic mapassisted cryptographic schemes have been highlighted in[33],and identity-based encryption schemes have been presented[34].Lately,Meshram et al.[33]presented an online/offline IBSS scheme based on a partial discrete logarithm.The scheme accepts pre-stored information for offline signature in a polynomial time.Furthermore,Meshram et al.[35]suggested an aggregation scheme for deployment in WSNs.The scheme requires lower computational resources and presents a faster processing time compared to the preliminaries.In recent times, a chaotic maps-assisted subtree-centric model for cryptosystems in cloud-based environments was proposed[36].In[37],fractional chaotic maps based on short signature schemes under human-centered IoT situations have been reported.Also,the authors[38]created an efficient and highly secured level subtree-based online/offline short signature procedure using chaotic theory.

There is no doubt that a few works related to the current paper have been reported.For instance,Maxwell’s source issue with random input data has been expanded leveraging conformally mapped polynomials[39].Also,conformal-based mapped polynomial chaos expansions have been carried out for uncertain dynamical systems [39].Additionally, conformal Chebyshev chaotic maps have been deployed for the robust construction of authentication protocol for healthcare telemedicine services[40].It is worth mentioning that Conformable Chaotic Maps(CCM)-based lightweight schemes are highly coveted to support the security of critical user information transmitted over 5G WSNs channels.However,the works[39–41]did not consider the application of conformable chaotic maps in the design of secure lightweight subtree-based online/offline signature procedure for massive devices in 5G WSNs as in the current paper.

3 Background and Material

The notations we utilize in our new procedure,SBOOSP using conformable chaotic maps under the fuzzy user data allotment for 5G WSNs,will be laid out in this section.Then we will go over some mathematical definitions and some fundamental notions of conformable chaotic maps.

3.1 Notations

Our SBOOSP for 5G WSNs uses conformable chaotic maps with fuzzy user data sharing.The following are the notations we used in our presented SBOOSP.When there is no doubt,we use[y,]as a shorthand for{y,y+1,...,},and[y]for[1,y].Allow Siɖ={iɖ1,...,iɖk}to be a set of(iɖ)identities that comprise all identities execution in iɖ for every iɖ =(iɖ1,iɖ2,...,iɖk), where iɖ is an identity vector.The position histories of iɖ in the model’s tree structure are defined as Iiɖ=The expected recipients form a subtree in a tree-organized identity-based signature/encryption procedure[38,42].In the tree structure,the identity vectors and the positions of their receivers are unified into T.Any genuine T must be able to cover the root node.This indicates that the PKG is in control of the structure.Also, T’s identity set and T’s position indices are denoted by ST= ∪iɖ∈TSiɖand Iiɖ= {i: iɖi∈ ST}.Similarly, the phrase Sup(iɖ)= {(iɖ1,iɖ2,...,iɖk′): k′≤ k} can be used to show that iɖ =(iɖ1,iɖ2,...,iɖk)is superior.Subtree T’s anticipated receivers are considered asSup(T)=∪iɖ∈TSup(iɖ).

Let us explore how the symbolizations work with the subtree-based architecture SBOOSP for massive devices in 5G WSNs.The proposed procedure is good for ensuring fuzzy entity data distribution while meeting security standards and specifications.Nevertheless, it has problems with multi-receiver efficiency.Assume the users are arranged in the tree structure,as indicated in Fig.1.To specify a prearranged user with iɖ=(B,F,),the position indices of iɖ and identity set are Iiɖ={2,6}and Siɖ= {B,F}respectively.The user builds a collection of Sup(iɖ)= {(B,F),(B)}that includes both herself/himself and her/his superiors.When a data owner delivers a message to a subtree like T={(B,G),(B,F),(A)},the message is sent to a set of receivers in that subtree.ST={A,B,F,G}and IT={1,2,6,7}are the identity set and location indices of T,respectively.T’s superiors are demarcated as Sup(T)={(A),(B),(B,F),(B,G)},which is the user contract that the proprietor of the data wants to express.

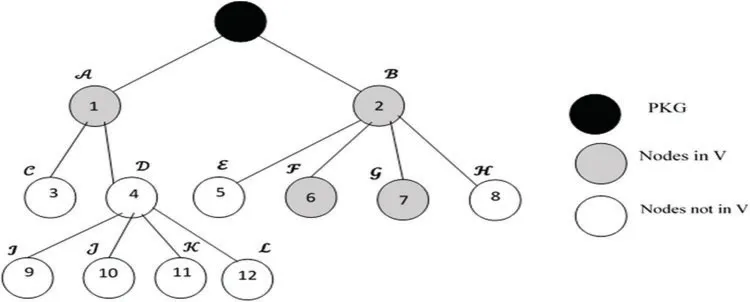
Figure 1:An illustration of a signature structure based on subtrees

3.2 Chebyshev Chaotic Polynomials

We examine the operatory of Chebyshev sequential polynomials(CSP)(see[43]).CSP T(y)is a-degree polynomial in the variant.Let ∈[-1,1]be the arrangement,and be an integer.CSP reported the following in general:

Under this circumstance,the functionalcos-1and cosrepresented ascos-1:[-1,1]→[0,π]and cos: R →[-1,1].

CSP[33,36–38,44]has two primary properties:chaotic and semi-group properties.

1.The chaotic properties:The CSP map is demarcated as[-1,1]→[-1,1]with degree＞1,is a chaotic map associated with the (invariant density) functionalfor the positive Lyapunov exponentλ=ln0.

2.The possessions of what is referred to as a semi-group satisfy the following conditions:

where ∈[-1,1]and a and c are positive integers.

Zhang[44]demonstrated that the semi-group property retains the interval(-∞,+∞),which may be used to improve the property as tracks:

and the semi-group property is also preserved.It is noteworthy that the extended Chebyshev polynomials also commute under conformation.

Chebyshev polynomials(CP)have two assessments that consider handling in polynomial time:

1.Given two elements and v,the discrete log’s(DL)task is to invent an integer a with the end goal Ta=v.

2.Because of three elements ,Ta(y),and Tc(y),the Diffie-Hellman problem(DHP)task is to measure the Tacelement.

3.3 Conformable Chebyshev Chaotic Maps(CCCM)

The conformable calculus(CC)was previously specified as conformable fractional calculus(CFC)[45].Nonetheless,it is straining the recognized properties for fractional calculus(derivatives of noninteger power).Fundamentally,CC takes the subsequent preparation:

Assume∈[0,1]is a fractional(arbitrary)number.If and only if δ0is the self-operator and δ1is the typical difference operational,an operatoris conformable differential.Clearly,δνis conformable if and only if,for differentiable utility.

Recently,Anderson et al.[45]offered a novel formulation of CC created by the control theory to designate the performance of proportional-differentiation controller conforming to the error function.The instruction has the following organization.

Definition 3.1Suppose that∈[0,1],then CC has in the subsequent documentation:

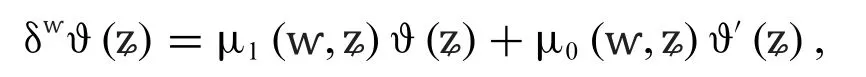
where the functions μ1and μ0attain the boundaries

The frequent formula(1)can replace by(2)

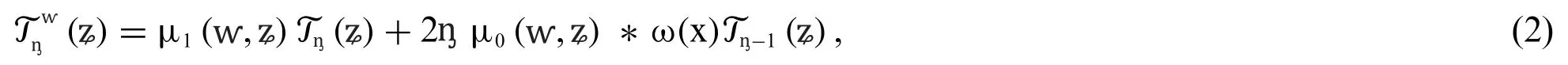
3.3.1 Properties of CCCM:TheCCCM has the Following Two Stimulating Possessions

Definition 3.2(Chaotic properties of CCCM).The Conformable Chebyshev Chaotic Maps fulfills the recurrent relations under chaotic property[46]i.e.,

Definition 3.3(Semi-group properties of CCCM).The semi-group properties look for CCCMs located on interval(-∞,∞)[46],i.e.,

Note that,when →0 is used,we get the original case from[44].

At this point,we note that the DL and assignments for the CCP are approximately DHP occur.

Figure 2:CCP for different values of =0.25,0.5,1 with =and

4 The Proposed SBOOSP Using Conformable Chaotic Maps

We will describe the novel efficient SBOOSP for massive devices in 5G WSNs that we have devised in this section.The plan is made up of five steps described as follows.

4.1 Setup

4.2 Extraction

The client’s private key is the pair(ξ,χ).It is worth noting that a properly created secret key must satisfy the following equality:

4.3 Offline-Signing

In the offline stage,the signer does the following calculation:

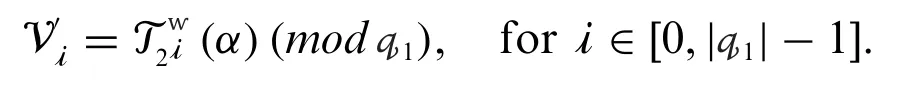
At the offline phase,we do not need the private key or knowledge of the message.It can also be considered a public parameter prepared by the(trusted)PKG rather than the offline-signing step.

4.4 Online-Signing

At the online phase,to register a message M ∈(-∞,∞)using(ξ,χ),the signer selects x ∈Rat random.Let x[i] be the ithbit of x.Describe Y ⊂{1,...,|1|} to be the set of indices such that x[i]=1.

The signature ɕ is(V,ξ,k).

4.5 Verification

To verify the signature ɕ =(V,ξ,k)foriɖ and M,the verifier initially calculatesζ=(V,ξ,M)and determines whether

If it is equal,accept it.Reject otherwise.

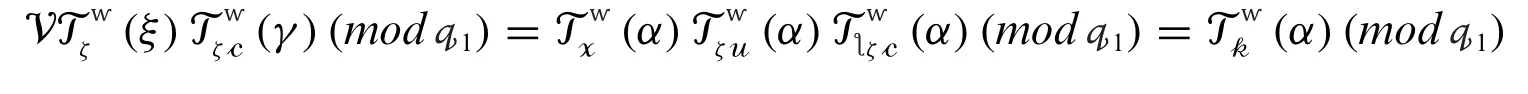
Remark 1.Following earlier discussions in this paper, any trusted third party can execute the offline signing algorithm as no secret data is required.Additionally, offline data can be reused gainfully.In practice, If the offline signing stage, which the PKG handles, is included in the setup process(and the offline data is placed as part of the public parameter).The suggested technique is a usual identity-based signature procedure with a fast-signing process that does not need exponentiation.

5 Security Investigations and Discussions

To demonstrate that our novel SBOOSP based on conformable chaotic maps is secure,we employ the Bellare et al.[47]acquiesced security proofs.

ands—Signing Oracle (SO) signing inquiries,—hashing inquiries,E—Extraction Oracle (EO)inquiries measure chaos,andτis the time to do an exponentiation operation.

(ξ,χ)is generated as a secret key for iɖ ∈ Sup(T)by B, and the uniformity assessment(ξ,(ξ,iɖ),χ,iɖ)is saved in a list by B.

Cost Reduction Investigation:The random oracle’s consignmentξ,iɖ)is irregular, requiring a mutual probability of at leastThis is assumed in the simulation procedure with extraction oracle failures.The simulation technique is effectivetimes(as a result of the fact that(ξ,iɖ)can also be asked in the signing oracle if iɖ ∈Sup(T)is not demanded in the extraction oracle),with the probability being:

The exponentiations used in the signature and extraction operations determine the process B’s temporal complexity,which is the same as:

6 Aggregation Procedure(Agg-SBOOSP)of the SBOOSP for 5G WSNs

It would be highly advantageous if a sensor node (SN) could sign not just one butiseparate messages simultaneously, with the aggregate signature having the same length as a single message’s signature or substantially shorter than the length of a single signature multiplied byi.Such an aggregate signature is essential in massive devices in 5G WSNs since it can drastically reduce sensor node communication overheads.This paper presents the new online/offline identity-based aggregation strategy for the proposed SBOOSP using conformable chaotic maps.It is made up of the five segments listed as follows.

6.1 Setup

6.2 Extraction

6.3 Offline-Signing

6.4 Online-Signing

6.5 Verification

If it is equal,accept it.Reject otherwise.

7 Performance Investigation

We compare our new SBOOSP to six previous strategies proposed by[33,38,48–51],in this section.We also compare our presented Agg-SBOOSP (extended SBOOSP) procedure to five other related strategies proposed by [33,38,48,50,51], respectively, to demonstrate the efficacy of our innovative design.The notationsare utilized to present our evaluation results.In the signature (online and offline) stage and verification stage, we represent the execution time for a group modular exponentiation, a bilinear pairing operation, a chaotic map operationa modular multiplication,and a one-way hash function.It is worth noting that the signature and verification steps are the only ones that require more computing power than the setup and extraction stages.By comparing the computational costs of our present SBOOSP to the works of[33,38,48–51],we look at the steps of signature and verification.In a similar vein,we compare our new presented Agg-SBOOSP with the works of[35,38,48,50,51].

Tab.1 shows the proposed SBOOSP’s functionalities, and Fig.3 compares the computational costs of existing relevant protocols [33,38,48–51].Tab.2 also includes a functional study of the proposed Agg-SBOOSP,as well as a comparison of computational costs in Fig.4 with other relevant protocols [35,38,48,50,51].We arrive at the following computation time statistics with unit hashing time based on the results of the experiments in [46,52,53]:The following is the order of computational complexity in this method:Recall the running time of hash is 0.06 ms[46,52]and that[ =0.5].References [33,38,48–51], and the SBOOSP, respectively, have total communication costs of 108.57,144.9,466.08,315.48,1.35,1.05,and 0.85 ms.References[35,38,48,50,51],and the Agg-SBOOSP have total communication costs of 108.57,279.87,351.72,108.57,1.26 and 1.06 ms,respectively.

Based on the classical results in [46,52,53], we arrive at the following computation time values with unit hashing time:

Table 1: Computational cost assessment of SBOOSP with other procedures

Figure 3:Communication cost(ms)analysis of SBOOSP with other procedures

As indicated in Fig.3,the interaction value of the suggested SBOOSP is the lowest attained.The tests frequently transform into runtime excels the rest of the linked procedures when using the proposed SBOOSP.Similarly, as the study results in Fig.4 reveal, the interaction value of the suggested Agg-SBOOSP is the lowest.The proposed Agg-SBOOSP frequently transforms tests into runtime and outperforms the other related procedures similar to the SBOOSP.It is interesting to note that the results presented in this paper show related characteristics to the results reported in[54].Next,we shall examine the basic setting for implementing the proposed SBOOSP in massive devices in 5G WSNs.

Table 2: Computational cost assessment of Agg-SBOOSP with other procedures

Figure 4:Communication cost(ms)analysis of Agg-SBOOSP with other procedures

8 Implementation for Massive Devices in 5G WSNs

8.1 Basic Setting

In a single-hop context (see Fig.5), each SN can sign messages with its private signing key accompanying its iɖ identifier information.According to our assumptions,the system parameter is created by the base station(BS).It is integrated with each SN when installed—assuming that either the sensor nodes or the base station can verify the signatures created by the SNs.As with 5G WSNs,we suppose that the BS is robust to computationally complex cryptographic processes,whereas the SNs have limited computing,memory,and battery power resources.Also,we assume that the BS’s private key is safely stored in a trusted server.

The main components of the 5G wireless access network are the 5G access and core networks,as depicted in Fig.6.In the 5G access network,two nodes called Next Generation evolved NodeB(ngeNB)and Next Generation NodeB(gNB)are described briefly.In this configuration,the new radio(NR)user plane and control plane procedures and functions for 5G network users are provided by the gNB.Similarly,the NR user plane and control plane procedures and functions are provided by the ngeNB for the 4G network users.As illustrated in Fig.6,the interface among ng-eNB and gNB is called the Xn interface.The 5G core network part of the configuration in Fig.6 comprises several nodes such as the 5G core Access and Mobility Management Function (AMF) and User Plane Function(UPF) [55].The function of the AMF involves accessing mobility management functions for access control and mobility management.The management of sessions associated with network policies is conducted by the session management function(SMF).Additionally,the UPF performs the user plane functions and can be deployed to different configurations and locations in the 5G wireless network.The proposed system model comprises the registration center(RC),the 5G Massive Devices(MDs),and the 5G core network (5GC).The RC is the entity designed to conduct honest and trust-based functions.The primary function of the RC is to register and or generate system parameters for the massive devices and the AMF based on their identities.The MDs transfer user information to the core network via the ng-eNB.Additionally, the AMF aggregates authentication on the user information received from the MDs and ensures the decryption of the authenticated data holistically.The proposed SBOOSP scheme can be deployed in this setting to provide efficient and robust security for MDs in 5G wireless sensor networks.

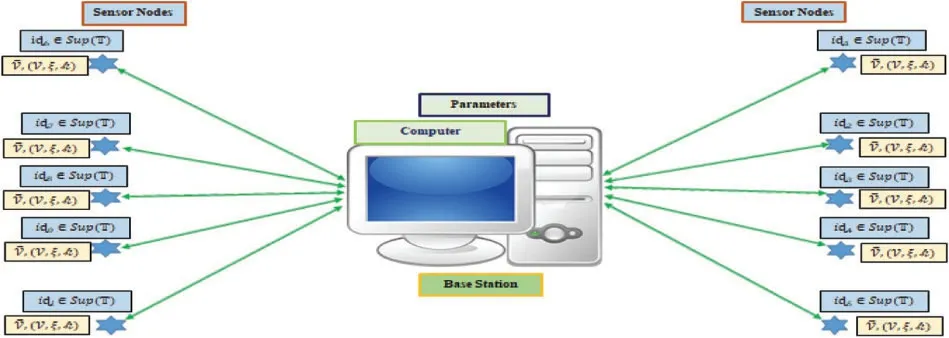
Figure 5:Overview of system implementation

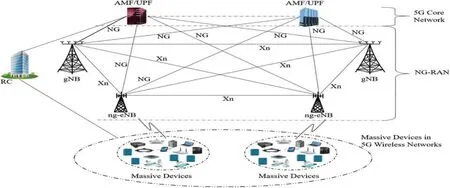
Figure 6:Basic setting of massive devices in 5G wireless networks for the proposed SBOOSP scheme

9 Conclusion

For massive devices in 5G wireless sensor networks with fuzzy user data sharing, this paper presented a new provably secure,lightweight SBOOSP and its aggregation(Agg-SBOOSP)leveraging conformable chaotic maps.In our proposition,each procedure is carried out with the fewest possible operations,thereby reducing the computational processing time of the scheme.Results indicate that the SBOOSP technique performs efficiently and independently of a certificate to verify and validate the signature without requiring pairing operations.As a result,the SBOOSP provides strong security in the random oracle paradigm with high unforgeability when a message is chosen.Additionally,the SBOOSP achieves multi-time offline storage at minimal complexity.Consequently, the signer can utilize the offline pre-stored information in polynomial time,demonstrating a significant advantage over most existing online/offline signature procedures that only allow for a single signature attempt.Furthermore, the new procedure allows for a secret key during the pre-registration process, but no secret key is necessary during the offline stage.The results of the performance investigation of SBOOSP and Agg-SBOOSP approaches are excellent.In comparison to various contenders, the proposed procedures have the lowest computing costs.Finally, both informal and formal security investigations of the proposed procedures demonstrate that the schemes can withstand all well-known attacks with exceptional security features at the lowest communication costs.Future work would focus on an efficient,lightweight,provably secure identity-based online/offline short signature procedure for massive devices in 5G WSNs using the concept of SBOOSP.

Acknowledgement:The authors would like to thank anonymous reviewers of Computers,Materials&Continua Journal for their careful and helpful comments.We extend our gratitude to the Deanship of Scientific Research at King Khalid University for funding this work through the research groups program under grant number R.G.P.1/72/42.The work of Agbotiname Lucky Imoize is supported by the Nigerian Petroleum Technology Development Fund(PTDF)and the German Academic Exchange Service(DAAD)through the Nigerian-German Postgraduate Program under Grant 57473408.

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.