PSO Based Multi-Objective Approach for Controlling PID Controller

Harsh Goud,Prakash Chandra Sharma,Kashif Nisar,Ag.Asri Ag.Ibrahim,,Muhammad Reazul Haque,Narendra Singh Yadav,Pankaj Swarnkar,Manoj Gupta and Laxmi Chand

1Indian Institute of Information Technology,Nagpur,India

2School of Computing&Information Technology,Manipal University,Jaipur(Rajasthan),India

3Faculty of Computing and Informatics,University Malaysia Sabah,Jalan UMS,88400,Kota Kinabalu Sabah,Malaysia

4Faculty of Computing&Informatics,Multimedia University,Persiaran Multimedia,63100,Cyberjaya,Selangor,Malaysia

5Maulana Azad National Institute of Technology,Bhopal,India

6Department of Electronics and Communication Engineering,JECRC University,Jaipur(Rajasthan),India

Abstract:CSTR(Continuous stirred tank reactor)is employed in process control and chemical industries to improve response characteristics and system efficiency.It has a highly nonlinear characteristic that includes complexities in its control and design.Dynamic performance is compassionate to change in system parameters which need more effort for planning a significant controller for CSTR.The reactor temperature changes in either direction from the defined reference value.It is important to note that the intensity of chemical actions inside the CSTR is dependent on the various levels of temperature,and deviation from reference values may cause degradation of biomass quality.Design and implementation of an appropriate adaptive controller for such a nonlinear system are essential.In this paper, a conventional Proportional Integral Derivative(PID)controller is designed.The conventional techniques to deal with constraints suffer severe limitations like it has fixed controller parameters.Hence, A novel method is applied for computing the PID controller parameters using a swarm algorithm that overcomes the conventional controller’s limitation.In the proposed technique,PID parameters are tuned by Particle Swarm Optimization (PSO).It is not easy to choose the suitable objective function to design a PID controller using PSO to get an optimal response.In this article,a multi-objective function is proposed for PSO based controller design of CSTR.

Keywords: Particle swarm optimization; multi-objective PSO; continuous stirred tank reactor;proportional integral derivative controller

1 Introduction

The domain of Chemical engineering always carriages more significant challenges to prevent environmental pollutants and protect its stability with the use of various modeling and control methods.In addition,it can significantly profit the living style and health conditions of humans[1–4].CSTR is a fundamental process system significantly employed in various process industries as well as chemical plants.It has a highly nonlinear characteristic, which is why it involves complexities in its design and control.Dynamic behavior is highly sensitive to variation in system parameters,requiring more effort to design a suitable controller for CSTR [5–7].In process industries, conventional PID controllers are widely used in different applications if the process is linear and time-invariant [8,9].Calculation of the PID gains using several tuning methods has been proposed.Firstly, the classical tuning law was given by Ziegler and Nichols,and another method was proposed by Cohen[10].

In these conventional offline PID tuning methods,tuning of PID parameters are often not suitable for nonlinear and time-varying systems [11].In such a system, the system parameters are normally changed with the time that needs continuous monitoring and online PID tuning accordingly.Due to this problem,various control techniques based on metaheuristic methods have been employed to find the optimum solution and enhance the controller’s performance.These AI techniques comprised of Differential Evolution (DE) algorithm [12–15], Genetic Algorithm (GA), PSO, and Artificial Bee Colony (ABC) [16–19].Even Nowadays, scientists and researchers are using AI techniques for solving future-driven network security attacks like distributed denial of service (DDoS) attacks[20–23].Furthermore, AI can implement using software-defined networking [SDN] [24–31], named data networking (NDN) [32–34] and cloud computing network [35] with voice over IP (VoIP)[36–39]fiber optic[40–42],worldwide interoperability for microwave access(WiMAX)[43–45],swarm intelligence (SI) [46], Deep learning (DL) [47], robotic system [48], and Satellite [49].In order to estimate the PID controller performance, an objective function is used in the AI techniques as mentioned above.A performance criterion that decides the optimal solutions is selected as an objective function.

Most of the functions are obtained from the analysis of error signals ranging among the desired output and the input signal of a system[50].Performance indices in terms of system error are defined as Integral of Squared Error(ISE),Mean Square Error(MSE),Integral of Absolute Error(IAE),Integral of Time Multiplied by Absolute Error(ITAE),Integral of Squared Time Multiplied by Squared Error(ISTE)and Integral of Time Multiplied by Squared Error(ITSE).IAE and ISE criteria weigh all errors consistently over time.Therefore, it may respond with enormous settling time ts and less overshoot Mp, which ITAE and ITSE can overcome, but the desired stability margin is uncertain.Zwe-Lee introduced a new performance criterion based on time response specifications of the system’s step response[51].Zamani et al.projected a generalized performance measure to ease the regulator of time and frequency domain conditions[52].Eight terms objective function has been introduced with two frequency parameters in above mention papers.A weighting factor determines the importance of each term.

On the other hand, the weighting factor’s selection for the objective function is a challenging job.This manuscript is objectively focused on the temperature control of the reactor.In the presented methodology,the temporary reaction of a plant is superior by scheming an appropriate PID controller.Multi-objective PSO MOPSO-PID optimization algorithm is recovering rise time tr, settling time ts, and maximum overshoot Mp.The remaining of the manuscript is organized as below.Section 2 discusses the mathematical modeling of the reactor in elaborated form.Section 3 shows the regulator of the reactor based on the traditional PID controller.Section 4 shows the Design of an Adaptive PSO-based PID controller and Proposed MOPSO-PID Controller, and Section 5 is based on the comparative study of results obtained by diverse control systems.Lastly, a summarized inference is discussed in Section 6.

2 Literature Review

The conventional approaches to deal with constraints suffer severe limitations and hence are the motivation of researchers to seek more flexible and powerful algorithms.A recent approach was Bioinspired intelligent computing that from its starting was continuously installed in various applications.Fuzzy logic has come as a powerful tool to mitigate the issues mentioned.The global interest in fuzzy logic demonstrates the academic and industrial performances of approximate reasoning over crisp assumption models in real environment applications.The fuzzy controllers in their industrial implementation are employed as intelligent controllers in real controlling applications.With low computational cost, fuzzy logic is highly flexible in dealing with complex non-linear problems.The performances are strictly according to the expertise of a developer that generates rules basis and hence is a subject of interest for most researchers[53].

The adaptive approaches for controlling the non-linear CSTR system depend on its parameters according to the system’s actual state during control.The polynomial approaches are confronted for controller design, and the satisfaction of initial control requirements is considered.Moreover, the systems with negative properties(for example,non-minimum phase behavior or process that consumes additional time)provide more accurate outputs.The subsidiary pole placement method also furnishes the requirements such as stability, asymptotic tracking of reference signals, and compensation of disturbances [54–56].The objective is to control the temperature and concentration in CSTR.In the proposed approach, the transient response of the CSTR plant is improved by designing suitable controllers like PID and adaptive PID controllers using PSO optimization algorithms by achieving less tr,ts,and overshoot.

3 Modeling of System

Utmost commonly employed chemical reactors in the industry are the entirely agitated and irreversible exothermic with CSTR.The system comprises a reactor with a cooling cover.The dissolution process of a manufactured item ‘A’into another manufactured item ‘B’arises in the CSTR and is shown in Fig.1.Generally, the response is heat-releasing.So, the temperature should be managed through flowing liquid and the cooling jacket that encloses the reactor wall.The primary purpose is to adjust the concentrationCAand temperature in the reservoirTRof the manufacturing item at the outlet by deploying the cooling rateFcand flow rateFL[17].

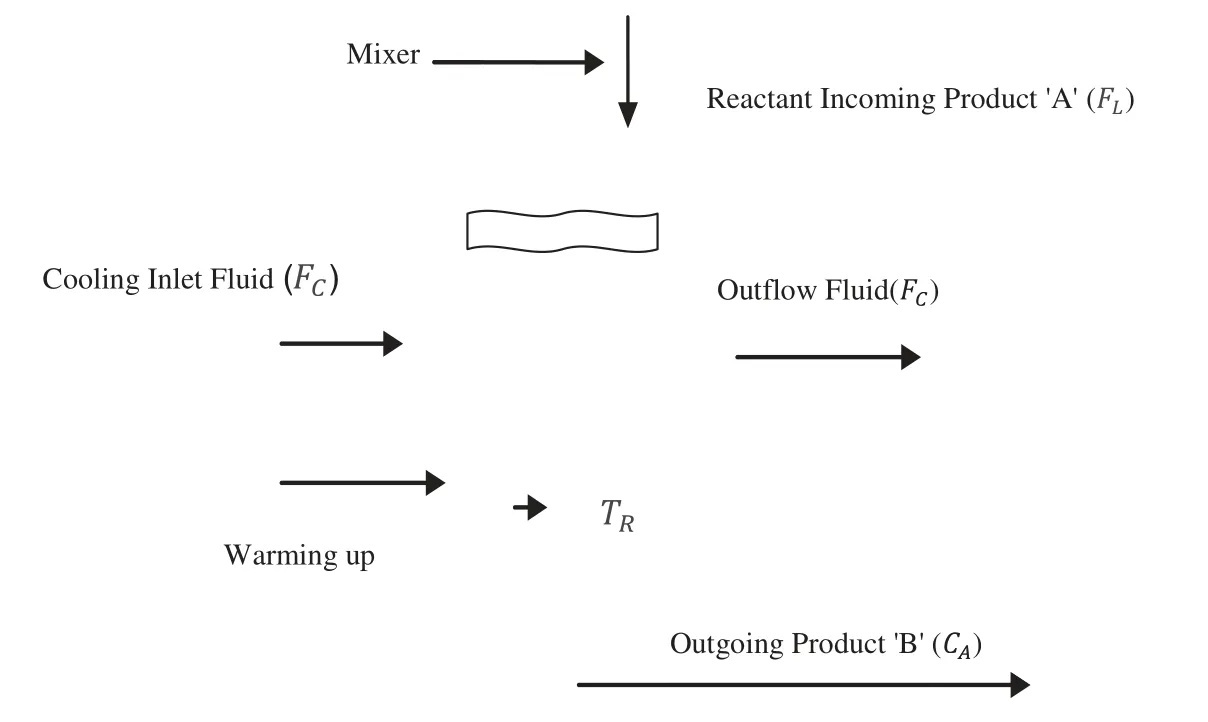
Figure 1:Strategic diagram for the CSTR

CSTR Modeling

The progress of the preliminary model is founded on some assumptions:This is entirely restless;the mass density of the input module is denoted byρand the volume of liquid in reactor isV.The level of reaction(r)is of order one by a port toAis given by:

where,k(reaction rate)

By Arrhenius law:k0is the frequency factor,Eais the activation energy,R:is the universal constant of perfect gases andTRis the temperature of the reaction mixture.

The dynamic performance of the device is depicted through generalized nonlinear differential Eq.(3):

where,TRis thereactor’s temperature,CAiis the concentration of flow,Ais the surface of conversation among reactor and double jacket,ΔHis Enthalpy,CAis the Concentration of product at exit,Uis the heat factor for exchange among reactor and double jacket,Tiis the streamed temperature in the device of reactor.

The second-order transfer function of the CSTR plant,commonly used for simulation studies for standard data specification,is obtained below[12,18].

4 Control of CSTR

The schematic design of the control scheme for CSTR is presented in Fig.2.In this article,the key objective is to stabilize and regulate the reactor’s temperature.The desired step r(t) input is applied, then response c(t) of the reactor is managed by auto-tuned PID controller through a feedback loop.Consequently, an error e(t) is caused by comparing the required temperature and the actual temperature of the reactor, which is fed to the PID controller.The optimized values of controller parameters are calculated by PSO using the objective function defined by Eq.(11).The corresponding response is the novel set theme or the plant’s input temperature.The reactor is then deployed accordingly to set a new value of temperature until the error is minimized.The performance of the reactor is analyzed in terms of time response specifications settling time ts, rise time trand maximum overshoot Mp.

Figure 2:Plan diagram for CSTR

5 Design of Adaptive PSO Based PID Controller

This section first describes the working of conventional PID controllers and mentions the parameters to be tuned by PSO.Finally,the proposed Multi-objective PSO(MOPSO)based adaptive PID controller design is presented in detail.The control signal generated by the controller is the function of these tuning parameters(Kp,Ki,Kd)is shown by Eq.(5)

Kp:Proportional Gain

Ki:Integral Gain

Kd:Derivative Gain

t:Time

These PID parameters are chosen to meet prescribed performance criteria for system response.This paper emphasizes the applications of PSO for tuning the controller.This algorithm(inherently)calculates PID parameters’values based on their prior states [9–11].Analysis of the process control system is generally based on its transient(dynamic)response.Several time-domain specifications are utilized for the investigation of the step response.These parameters are tr,ts,Mp,and steady-state error Ess.The system’s step response can be improved by optimizing the time domain specification,which depends on the designing suitable controller.Two significant factors can express the transient response of the CSTR;firs,t the speed of response(characterized by the trand tp),and second is the nearness of the response to the reference input(represented by the Mpand ts)[3,21].The error signal is given by(6)as below:

The IAE and ISE weight all errors are objective of time.Hence, optimizing the response using ISE and IAE can occur in small tsbut prominent Mpor vice versa.Thus, ITAE and ITSE conquer the drawback of the IAE and ISE.Further, ITSE and ITAE are trying to reduce the squared error signals and weighted absolute,respectively.However,it is not necessary to minimize all the response specifications such as Ess, Mp, tr, and tsat the same time.Therefore, the multi minimum problem can be overcome by using a weighted sum of frequency and time response specifications objective functions.M.R.Haque et al.[21] presented the performance criterion described by the objective function of Eq.(7).

This fitness function is optimized to tune the PID parameters for getting the minimum values of time response specifications.To get the appropriate values ofKp,Ki,Kd,every swarm of the population is calculated with the help of an objective function [3,21].For getting the PID gain values, a fitness function is derived by Eqs.(7)and(8)

where,Trefis required value of plant temperature set by controller designer and T0is real temperature.

Proposed MOPSO-PID Controller

In 1995, the heuristic method PSO was proposed by James Kennedy.As shown in Fig.3, the candidate resolution of the existing search space for the evaluation is completed by the repetition procedure.In order to fit the task’s requirements,minima and maxima of the objective function are obtained by the candidate’s solution.PSO does not allow the objective function in the form of its inputs, so the minimum and maximum (locally/globally) are randomly away from the solution.The user does not know the solution.At each level, the position and speed of the candidate’s solution are kept;also,update fitness value.PSO has recorded the best value of fitness on behalf of a specific confirmation.The other specific distinct approach to this value is the most acceptable solution and situation.This value is recognized during the global best candidate solution along with the global best position.The up-gradation of best fitness value is carried out,local and global best fitness values are substituted if required.For the best performance of PSO’s optimization,the up-gradation of position and speed is essential.By using Eq.(7)updated each particle’s velocity[17–19].

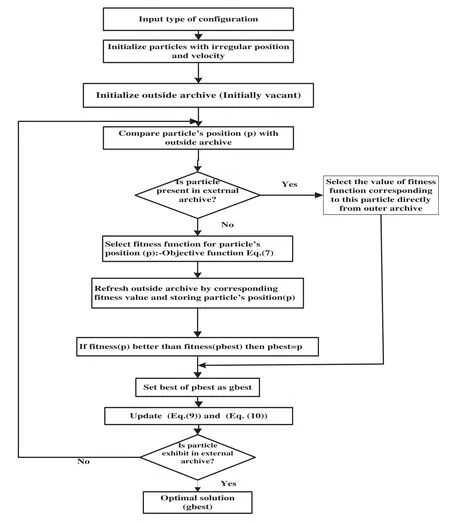
Figure 3:Tuning of controller parameters using PSO

PSO is initialized with the first position and velocity using random solutions,which is named the swarm.PSO algorithm has three steps.Which following three steps are iterated until the criterion of termination is done:

Step 1:Evaluate the fitness of each particle which is by the Multi-objective performance criterion.

Step 2:Accordance with achieved best positions,update every particle by two values.

(1) The best solution(fitness)achieved so far is named pbest.

(2) The best value obtained so far by any particle in the population named as gbest.

Step 3:Update the position and velocity of every particle.The velocity and position are updated as follows:

where g(t), xi(t), xi (t), and vi (t) represent the global best, position, personal best and velocity,respectively ofndimension of it h particle, c1 and c2 are acceleration coefficients, r1 and r2 are uniformly distributed random no.in the interval [0,1], X is the constriction factor [3,21].In this work,a PID controller is designed with the help of MOPSO to enhance the performance of reactor.The PSO is specifically used to find out appropriate tuning parametersKp, Ki,andKdsuch that the optimal performance of the controller can be achieved.Individual string and Evaluation function can be described as follows:

(a)Individual String:The controller parameters compose an individualKsuch asK=[Kp KiKd];hence, there are 3 members of an individual.These members are chosen as true values.The dimension of a population isn×3 because there arenindividuals in a population.

(b)Evaluation Function:The evaluation value of each individual in the population defined by Eq.(13).The performance criterion J(k)as in Eq.(7)is a reciprocal of the evaluation function‘f’as in Eq.(13).It means the higher J(k)the value of individual k,the smaller its evaluation value.The evaluation function is given by Eq.(13).

This work proposes a MOPSO-PID controller for probing the optimized values of PID controller parametersKp,KiandKdwith the help of PSO for CSTR.Each individualKcomprises 3 membersKp,KiandKd.The searching phenomena of the designed MOPSO-PID controller are given as under:

Step 1.Upper bounds(Ub)and lower bounds(Lb)for the PID tuning parameters are specified and initialize the individuals of the population randomly along with searching, velocities,pbestandgbest.

Step 2.For every initial individual K of the population, apply the Routh-Hurwitz criterion to examine the stability of closed-loop plant and determine the values of the response specifications namelyMp,Ess,trandts.

Step 3.In the population,measure the evaluation value of each individual using the Eq.(13).

Step 4.Each individual’s estimation value is compared with its pbest.The best estimation value between the pbest is indicated as gbest.

Step 5.According to Eq.(9)improve the member velocity‘v’of each individual.

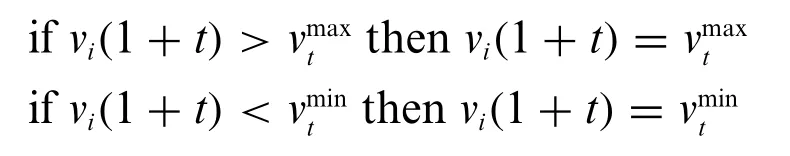
Step 6.Adjust the position of member for each individual“K”by Eq.(10)

whereandshows theLbandUb,respectively member‘i’of the individualK.

Step 7.If the no.of repetitions approaches the highest,then go to step 8.If not,go to step 2.

Step 8.gbest is the optimal controller tuning parameter generated by the individual [6,20,22],presented in Fig.3.

6 Result Analysis

This segment shows outcomes by MATLAB programming, and a comparative investigation is completed to express the supremacy of the projected MOPSO control system.MATLAB programming is done for the parameters of CSTR given in the appendix.Initial parameters of the PID controller and PSO algorithm for visual examination are shown in Tabs.1 and 2.PID controller parameters presented in Tab.2 for conventional PID are found by the offline tuning method(Z-N).

Table 1: Constraints of particle swarm optimization for the plant

Table 1:Continued

Table 2: Constraints for conventional PID and MOPSO-PID

CSTR Performances with Different Controllers

The time response curve of Fig.4 shows the performance of CSTR with conventional PID and proposed MOPSO-PID.The preliminary temperature of the reactor is considered as 40oF.The desired temperature is set to 80oF.It can be observed that without any controller, the reactor temperature is not reaching its desired value.With the application of a conventional PID controller, the desired temperature is achieved,but there is an overshoot of 14.46%,while with the proposed MOPSO-PID controller,this overshoot is reduced to 2.14%.The minimization of error takes a response time of 0.42 sec by MOPSO-PID for achieving the required temperature of 80◦F.

Figure 4:Comparative analysis using temperature vs.time graph

The CSTR system’s response for without controller, conventional PID, and the MOPSO-PID controller have been depicted in Fig.5.PID controller displays settling at 1.5 sec & MOPSO-PID displays the steady condition at 0.25 sec.The error reduced to zero after 0.5 s by MOPSO-PID, as revealed in Fig.6.Without any controller, ITAE and MSE are high with 15428.3682 and 267.6768,respectively, and with PID controller, error values of ITAE and MSE are 1642.1107 and 26.7112,respectively, as shown in Tab.3.It clarifies that the appropriate performance index can be achieved by implementing the proposed control scheme to CSTR.It shows that using a conventional PID controller for such a nonlinear system cannot produce satisfactory results while the help of adaptive mechanism desires performance can be achieved.Figs.7 and 8 reveals thattr,tp,ts,as well asMpare minimized due to the addition of the PID controller with Multi-Objective PSO.This is found that the fault figures should also decrease to a large extent.

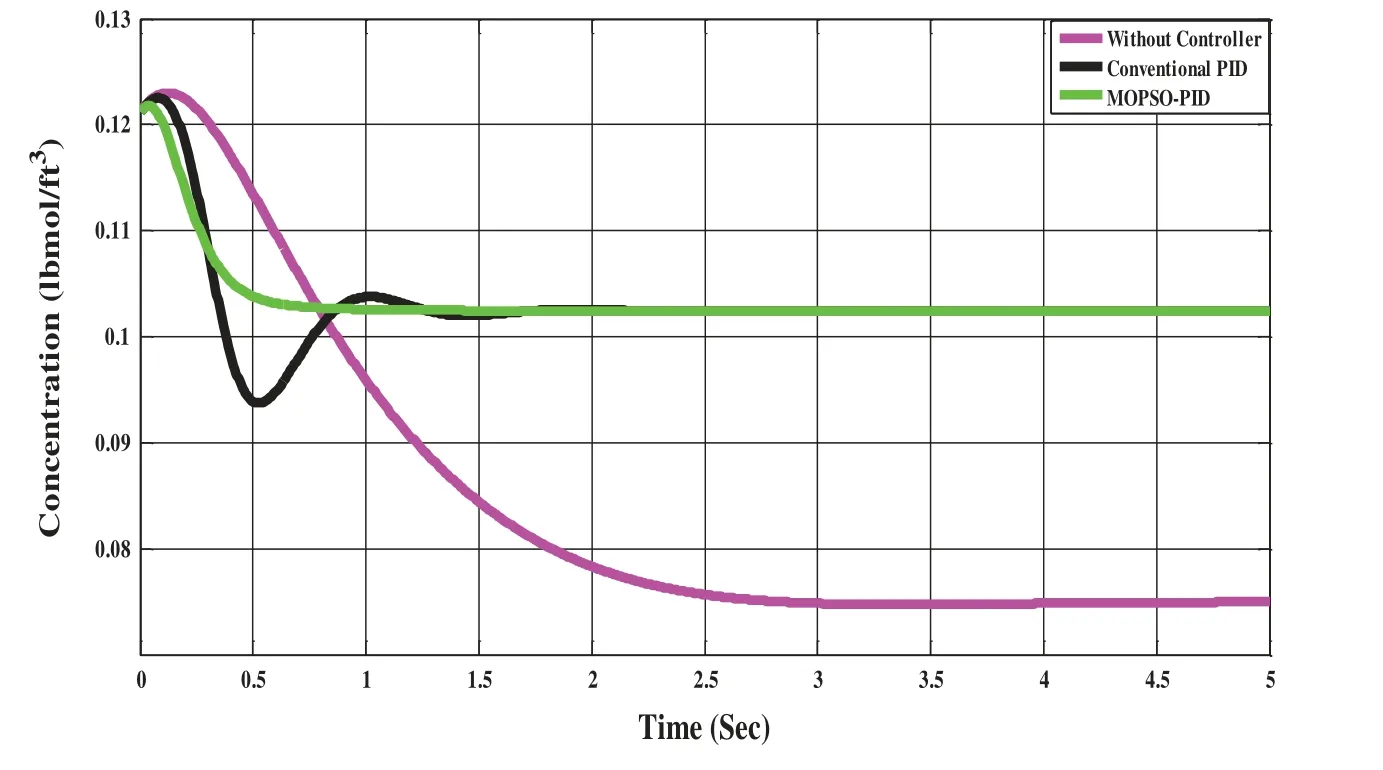
Figure 5:Comparison of the concentration of CSTR system

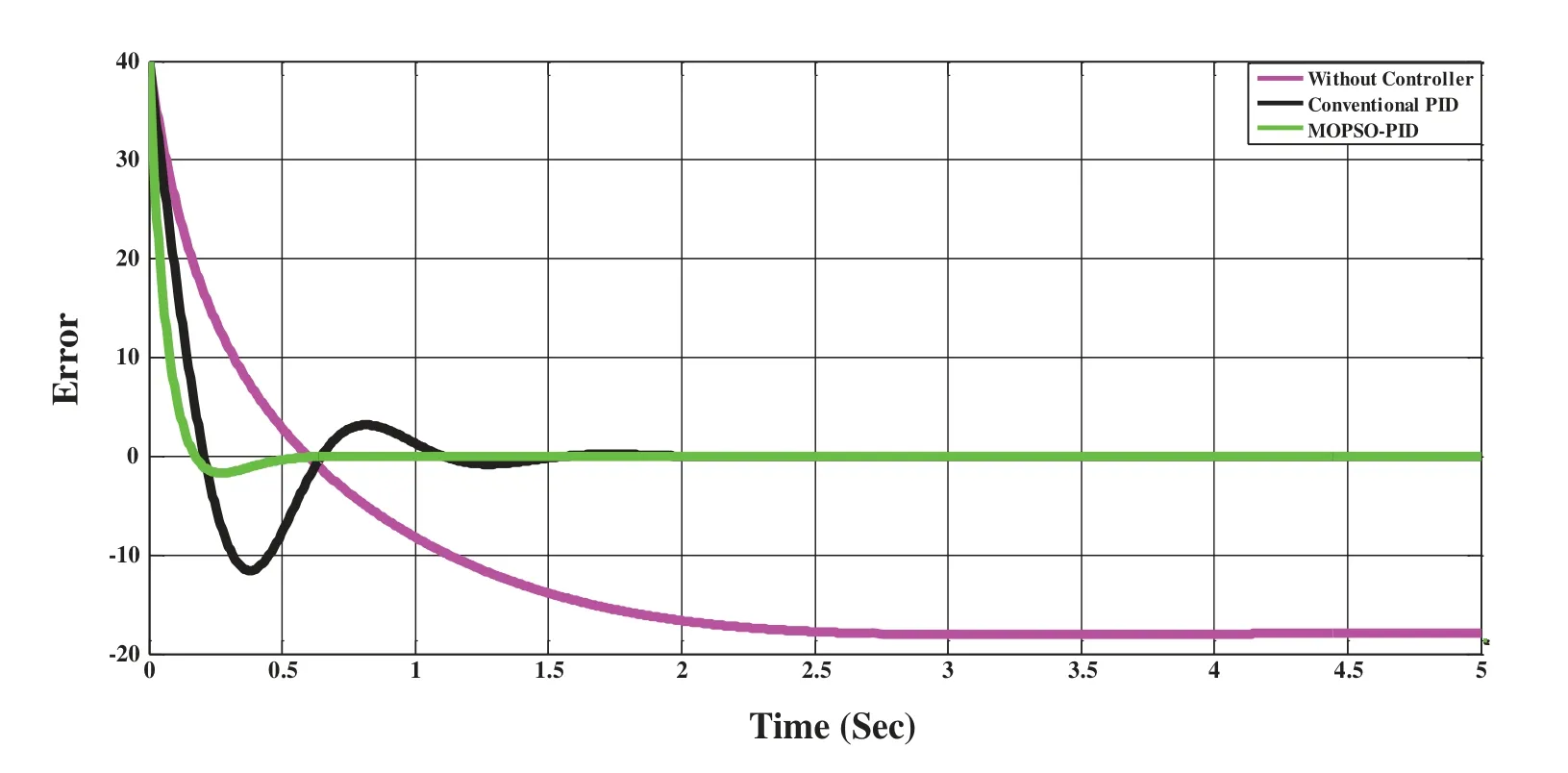
Figure 6:Comparative analysis using error vs.time graph

Table 3: Comparative analysis of MSE and ITAE

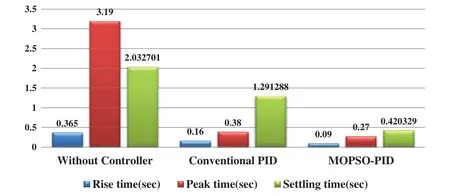
Figure 7:Evaluation of different approaches for response specifications

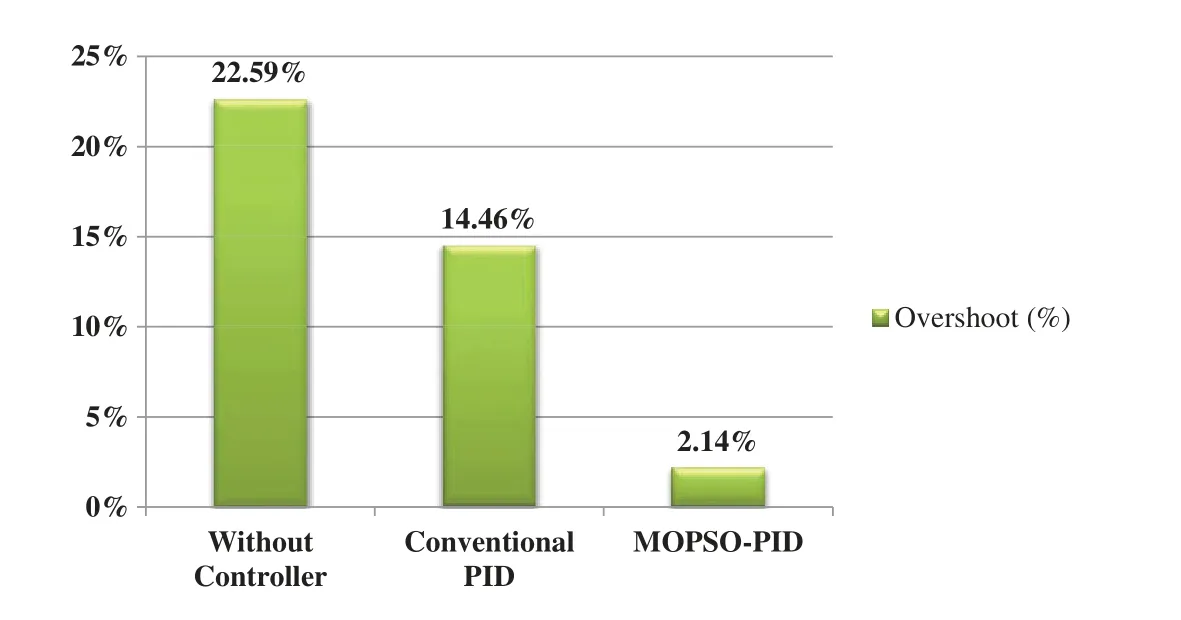
Figure 8:Assessment of overshoot by different control systems

7 Conclusion

This paper projected a temperature control technique due to the abrupt change in flow rate and temperature.The controller wants to be precisely adjusted to maintain the response temperature of the reactor at reference value.A novel approach is employed for calculating the PID controller parameters with the usage of the swarm algorithm.The proposed technique MOPSO-PID controller,integrates the new time-response specification with the PSO algorithm.The results graphically and analytically are analyzed using the reactor transfer function time response subjected to a unit step function.There is a remarkable improvement in more petite tr, tp, ts, and a lower Mpovershoot.Simulation results justify that the proposed MOPSO-PID controller can highly improvise the PID tuning optimization in comparison with a conventional PID controller.

Acknowledgement:The authors would like to thank the editors of CMC and anonymous reviewers for their time and review of this manuscript and Professor Dr.Yong-Jin Park(IEEE Life member and former Director IEEE Region 10)valuable comments and suggestions on improving the paper.

Funding Statement:University Malaysia Sabah fully funds this research under the grant number F08/PGRG/1908/2019, Ag.Asri Ag.Ibrahim received the grant, sponsors’websites: https://www.u ms.edu.my.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.