基于LLE和高斯混合模型的时间序列聚类

杨秋颖，翁小清

(河北经贸大学 信息技术学院，河北 石家庄 050061)

0 引 言

时间序列(TS)是从均匀的时间间隔和给定的采样率下测量收集的有序数据集，其研究遍及金融、医学、轨迹分析和人体动作分段等多个领域。时间序列聚类[1]是在没有任何先验知识的情况下分析大量时间序列数据的有效方法，其目的以某种方式将给定的数据集划分为一组不重叠的集群，从而揭示数据的底层结构。在进行聚类时合适的维数约简和相似性度量对聚类效果有重大影响[2]，但由于时间序列高维，高冗余以及存在非线性结构等特点，将传统的聚类算法直接用于此类数据时往往无法取得满意的效果。

维数约简根据是否存在变换矩阵，可分为线性和非线性两种。多维尺度变换[3]、主成分分析[4]等线性方法默认先进行投影变换，然后找到一个使其目标最大化的低维空间；但现实中绝大部分时间序列是非线性的，线性方法在应用时存在局限性。非线性降维方法[5]有核方法、神经网络和流形学习等，局部线性嵌入(Locally Linear Embedding，LLE)[6]是一种重要的流形学习方法。流形学习认为采样数据是由低维流形映射到高维空间得到的，其本质是从原始的高维数据中寻找产生数据的内在流形，并求出相应的嵌入映射。LLE假设采样数据分布在一个潜在的流形上，而流形的局部可以近似为欧氏空间，具有线性结构，故任意一点可以表示为其k近邻的线性组合，并能够在低维流形进行重构。LLE将高维的非线性结构映射到低维空间的同时很好地保留了其内蕴特征。

针对时间序列非线性和维度高的特点，该文提出一种基于LLE和高斯混合模型(Gaussian Mixture Model，GMM)的时间序列聚类算法LLE_GMM。首先从保留数据集局部结构的角度，使用LLE将每个高维时间序列样本表示为其k近邻的线性组合，并在低维空间进行重构，在保持数据集局部几何结构的同时实现维数约简；然后使用GMM从概率分布的角度进行聚类分析。将LLE_GMM算法与已有的非深度学习和深度学习算法进行了比较，在36个数据集上的实验结果表明，该方法对单变量时间序列具有更好的聚类效果。

1 背景和相关工作

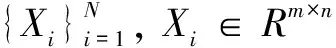
1.1 局部线性嵌入

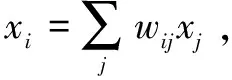
LLE算法的具体步骤为：

(1)寻找每个样本点xi的k近邻的集合。

(3)求低维嵌入Y。计算xi在其低维空间的嵌入点yi，使其重构的代价函数φ(Y)最小，即最小化式(1)：

(1)

这一优化问题可以通过对式(2)进行特征值分解得到。

M=(I-W)(I-W)T

(2)

一般的，M的第一个最小特征值为0，不能反映数据特征，故选M的第2到d+1个特征值对应的特征向量，即低维嵌入Y={y2,…,yd+1}。

1.2 高斯混合模型

高斯混合模型(GMM)假设数据集是有限个高斯分布的线性混合，每个高斯分布对应一个类。具体地，给定类个数C，对于给定的样本yi，GMM的概率密度函数定义为：

(3)

用EM(Expectation Maximization)算法估计GMM参数。其基本步骤如下：

(1)根据给定的C值，随机初始化每个簇的高斯分布参数(均值和方差)以及权重向量w。

(2)E步：计算数据点xi对每个簇的隶属度E[Zic]。隶属度越大，样本由该分模型生成的概率越大。隶属度公式如式(4)和式(5)所示：

(4)

(5)

(3)M步：用第(2)步计算得到的所有点对每个分模型Zc的隶属度更新模型参数，如式(6)～式(8)所示：

(6)

newΣc=

(7)

(8)

(4)循环执行(2)和(3)步，计算对数似然函数直到收敛。

GMM使用后验概率不断更新各个分模型的参数，最终得到MTS样本对各个类别的隶属度，从概率分布角度进行聚类分析。

1.3 相关工作

时间序列聚类大致可以分为基于实例、基于特征和基于模型的方法三种[8]。

基于实例的方法中，Azencott等[9]将基于图的拉普拉斯谱聚类与模拟退火相结合研究时间序列间的互信息，自动生成最优的时间序列聚类，但该方法只是适用于等长的有限数据集。考虑时间序列的非线性以及滞后问题，张贝贝等[10]将Copula函数引入识别动态相关结构的相似性度量。Guo等[11]推广了基于核的模糊c均值聚类算法，在动态时间对准核(DTAK)中嵌入非线性时间对准使得基于核的模糊c均值可以用于可变长度的序列。

基于特征的方法中，Chandereng等[12]考虑时间的滞后性影响时间序列的相似性，提出了一种滞后惩罚加权相关(Lag Penalized Weighted Correlation，LPWC)的聚类相似度度量方法，用于对随着时间推移表现出密切相关行为的时间序列进行分组。针对长度比较短且存在相位差的时间序列，Yang等[13]提出一种Shape-Distance Ratio (SDR)的相似性度量方法并结合k-Medoids (PAM)分区聚类算法实现时间序列聚类。Euan等[14]将谱理论与层次聚类相结合，提出层次谱合并(HSM)时间序列聚类算法。Duan等[15]用趋势滤波对时间序列进行最优分割和模糊信息粒化将原始数据转为粒状时间序列，提出基于线性模糊信息粒的动态时间扭曲(LFIG_DTW)距离的分层聚类方法，LFIG_DTW算法不仅可以检测距离的增减趋势，还可以检测距离的变化周期和变化速率。Caiado等[16]提出一种新的非参数的用于描述和比较长时间序列大集合的频域方法。Wang等[17]针对不等长区间值时间序列的聚类问题提出BRDTW算法。

Wang等[18]提出时间序列的稀疏子空间聚类算法(Sparse Subspace Clustering，SSC)，利用稀疏表示构造相似度矩阵再进行光谱聚类，将其运用到电影票房研究问题。稀疏编码字典学习中数据样本与字典原子的长度不一致以及存在时间延迟的问题，Yazdi等[19-20]提出基于非线性时间不变性kSVD (twi-ksvd)的稀疏编码字典学习时间序列聚类算法。

为了提取时间序列的形状特征，Zhang等[21]结合shapelet学习、shapelet正则化、光谱分析和伪标记的优点，扩展了监督式shapelet学习模型来处理未标记的时间序列数据，提出了无监督显著子序列学习(Unsupervised Salient Subsequence Learning，USSL)。Xiao等[22]结合时间特征网络和注意力LSTM网络提出一种鲁棒时序特征网络(RTFN)，将基于残差网络和multi-head卷积神经网络的时间特征网络用于提取序列的时态特征，attentional LSTM网络进一步提取时序中的shapelets特征，并将其用于分类和聚类。

在基于模型的方法中，Corduas等[23]针对传统的ARIMA模型中one-step-ahead预测函数可能导致对模型的错误描述，提出h-step-ahead预测函数，用h-step-ahead预测误差的参数的欧氏距离平方和度量时间序列的相似性。

基于监督学习的深度学习算法可以学习数据的隐藏特征。但现实中的时间序列大部分没有标签信息，因此基于监督学习的深度学习算法无法直接用于时间序列聚类。Xie等[24]提出Deep Embedded Clustering算法，以self-learning的方式定义聚类损失，同时更新网络和聚类中心的参数。然而聚类损失并不能保持局部结构，会导致嵌入空间的破坏。为此Guo等[25]使用under-complete的自动编码器来学习嵌入特征和保持数据生成分布的局部结构，提出了Improved Deep Embedded Clustering算法。

Sai等[26]提出深度时间聚类(Deep Temporal Clustering，DTC)，采用CNN自动编码器与BI-LSTM聚类层学习聚类表示。通过测量预测结果与目标分布之间的KL散度来设计聚类层；但直接转矩控制的性能很大程度上取决于编码器的能力，根据表示学习计算的预测分布在用来计算目标分布时存在不稳定性。为提高编码器能力，Ma等[27]将时间重构和K-Means聚类集成到seq2seq模型中，提出了时间序列辅助分类任务的伪样本生成策略，提高了编码器的能力。此外，Fortuin等[28]结合自组织映射(SOM)、变分自编码器和Markov模型，提出一种可解释离散表示学习。McConville等[29]采用流形方法提取特征，对重嵌入空间进行浅聚类。Ding等[2]将卷积神经网络在同一方向的输出变化次数转化为时间序列的相似性，通过优先收集少量的高相似度数据来创建标签，使用基于卷积神经网络的分类算法辅助聚类。

上述大多数方法或是未考虑时间序列的非线性结构，或是从保留全局特征的角度进行降维，没有考虑数据集的局部结构，而数据集的局部结构对聚类效果有较大影响；此外上述大多数方法从距离角度度量时间序列的相似性，该文在保留时间序列局部特征的基础上，使用GMM从概率分布角度进行聚类，提高了聚类性能。

2 基于LLE和GMM的聚类算法

基于LLE和GMM的聚类算法包括两步骤：首先从保留数据集局部结构的角度，使用LLE将每个高维时间序列样本表示为其k近邻的线性组合，并在低维空间进行重构，在保持数据集局部几何结构的同时实现维数约简；然后使用GMM从概率分布的角度进行聚类分析。算法的主要步骤如下：

算法1：LLE_GMM(X,C,k,d)。

输入：时间序列数据集。X={x1,x2,…,xN,xi∈Rm}，聚类个数C，近邻个数k，嵌入维数d。

输出：聚类结果。

Step1：对数据集X使用PCA算法去除噪声和冗余；

Step2：对任意xi的k个最近邻点xj，构造近邻集合；

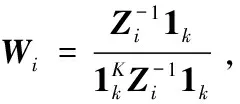
Step4：构造矩阵M=(I-W)(I-W)T，计算M的前d+1个特征值和对应的特征向量，则低维嵌入为Y={y2,…,yd+1}；

Step5：初始化高斯混合模型参数(w,μ,Σ)开始迭代；

Step6：E-step，求每个样本对每个类别的概率；

Step7：M-step，优化E-step的模型参数得到新的参数(w,μ,Σ)；

Step8：重复E-step和M-step，直到参数收敛或是达到最大迭代次数；

Step9：用训练好的GMM模型进行聚类。

上述算法分为降维和模型训练两个部分。对于时间序列数据集X={x1,x2,…,xN,xi∈Rm}，N为样本总数，m为输入样本维数。步骤1中使用PCA预处理的时间复杂度为O(Nm2)；步骤2-5为LLE降维，其中k近邻搜索的复杂度是O(mN2)，构造权重系数矩阵的时间复杂度是O(mNk3)，求解低维嵌入的时间复杂度是O(dN2)，d为嵌入维数；步骤5-9是构建高斯混合模型聚类阶段，时间复杂度与迭代次数有关，每次迭代过程分为E-step和M-step。E-step计算样本的所属类别概率的时间复杂度为O(NC)，C为类别个数；M-step更新参数w,μ的时间复杂度为O(k)；计算协方差Σ的时间复杂度为O(NCd2)，故每次迭代的时间复杂度为O(NC(d2+1)+C)；当迭代次数为h时，算法整体时间复杂度为O(Nm2+mN2+mNk3+dN2+hNCd2)。

3 实验结果与分析

在36个来自UCR[30]数据库的时间序列数据集上用Rand指数对聚类性能进行评估。用Matlab 2019b编写了所有程序，并在方正计算机(内存16 GB，CPU 3.30 GHz，Windows 7操作系统)上实现。

3.1 数据集描述

采用来自UCR数据库的时间序列数据集，数据集都具有非随机结构且提供聚类基准，即标签信息。表1列出了36个数据集的主要特征，包括序号、样本集名称、样本总数、样本长度和类别个数。这些数据集涉及工业、图像识别、人体行为识别、医学和化学计量学等领域。

表1 数据集概要情况

3.2 评价标准

为使文中算法与已有算法具有对比性，采用常见的外部方法Rand指数[31](RI)评价LLE_GMM的聚类效果。

(9)

式中，TP表示属于同类的样本的预测标签相同，FN表示属于同类的样本的预测标签不同，FP表示属于不同类的样本的预测标签相同，TN表示不属于同一类的样本的预测标签也不同。Rand指数取值为[0,1]，是正向指标，当原有的标签信息与预测结果完全一致时，RI=1。

3.3 性能比较

为检验LLE_GMM算法性能，将其与10种已有算法进行Rand指数(RI)比较，10种算法分为两个类型：基于非深度学习以及基于深度学习。其中非深度学习的分为基于实例和基于特征两种，基于特征的聚类算法又分为基于结构和基于形状两个方面。

表2给出了用5种基于非深度学习的方法以及LLE_GMM在36个数据集上进行聚类的RI值，六种方法的最高RI值在表2中加粗显示。表2中第1列的序号对应表1中的数据集，第2列至第6列分别为KSC[32]、NDFS[33]、RSFS[34]、kshape[35]、USSL[21]的RI值；最后一列给出了LLE_GMM的RI值以及对应的近邻个数k和嵌入维数d。

表2的倒数第2行Avg给出各种方法的平均RI值，可以看出LLE_GMM在36个数据集的平均RI为0.802 0，在六种非深度学习算法中取得最优结果。表2的最后一行Win给出各算法在36个数据集上取得的最优RI的个数，可以看出LLE_GMM在23个数据集上取得最优结果。

表2 与非深度学习方法的RI比较

续表2

表3给出了用5种基于深度学习的方法以及LLE_GMM在36个数据集上进行聚类的RI值，这六种方法的最高RI值同样加粗显示。表3中第1列的序号对应表1中的数据集，第2列至第6列分别为SOM-VAE[28]、N2D[29]、IDEC[25]、DTCR[27]和TSC_CNN[2]的RI值；最后一列给出了LLE_GMM的RI值以及对应的近邻个数k和嵌入维数d。

表3的倒数第2行Avg给出各种方法的平均RI值，LLE_GMM在36个数据集的平均RI在六种算法中同样取得最优结果。表3的最后一行Win给出各算法在36个数据集上取得的最优RI的个数，可以看出LLE_GMM在18个数据集上取得最优结果。

表3 与深度学习方法的RI比较

续表3

深度学习算法在执行时会一定程度上受到算力的限制，LLE_GMM在不依赖硬件设施的同时可以取得不差于深度学习算法的效果。

3.4 消融实验

LLE_GMM算法有LLE和GMM两个模块，为验证两个模块的有效性，分别设置GMM和LLE_Kmeans两个对照实验，实验结果如表4中第2和第3列所示。仅使用GMM模块，平均RI指数为0.715 6，相较于LLE_GMM下降了8.64%；LLE_Kmeans的平均RI指数为0.773 8，相较于LLE_GMM下降了2.82%。实验证明，GMM相较于Kmeans可以更好地拟合复杂的数据分布，发现椭圆形簇，提升聚类效果。加入LLE模块的GMM通过维数约简有效降低了数据冗余，更好地表达非线性数据的内蕴特征，提升了聚类效果。

表4 消融实验结果

3.5 参数对算法性能的影响

LLE_GMM算法有两个参数k、d，分别表示近邻个数以及嵌入维数。

图1给出了d=35在DiatomSizeReduction数据集上，以及d=16在DistalPhalanxOutlineAgeGroup数据集上，算法的RI值随近邻个数k的变化情况。从图1中可以看出，当k的取值过小时，RI值较小，考虑可能是过小的近邻个数无法保证时间序列样本在低维空间的拓扑结构；随着k的增大，RI值逐渐增大达到最大值，然后在一定范围内波动；但是当k值过大时，RI值呈现下降趋势，考虑近邻个数过大时无法体现数据集的局部特性。因此，LLE_GMM算法需要根据应用场景选择合适的k值。

图1 LLE_GMM算法RI值随近邻个数k的变化

图2给出了k=15时在coffee和Meat数据集上，算法的RI值随嵌入维数d的变化情况。从图2中可以看出，当d的取值过小时，RI值较小，考虑可能是过小的嵌入维数导致不同样本在嵌入空间相互交叠；随着d逐步增大，RI值快速增大达到最大值；随后当d值过大时，RI值呈现下降趋势并最终稳定在一定范围内，考虑信息保留过多影响对原始数据的特征表达，使得效果下降。所以LLE_GMM算法并不需要很高的嵌入维数就可以获得很好的聚类效果。

图2 LLE_GMM算法RI值随嵌入维数d的变化

4 结束语

提出了一种基于LLE和GMM的时间序列聚类算法。首先从保留数据集局部结构的角度，使用LLE将每个高维时间序列样本表示为其k近邻的线性组合，并在低维空间进行重构，在保持数据集局部几何结构的同时实现维数约简；然后使用GMM从概率分布的角度进行聚类分析。在36个数据集上分别与基于深度学习和基于非深度学习的算法进行对比，结果表明LLE_GMM的聚类性能好于已有算法。该文所提算法有两个参数k和d，人工选取参数耗时且可能无法获得全局最优，因此如何自适应地选择最优参数值有待进一步研究；同时GMM限制样本个数不得小于维数，如何在小样本高维数据上改进聚类效果仍需进一步探索。