基于传播属性的社交网络重要节点发现
2022-08-19王嘉瑞邢方远许建婷张克君
钱 榕,王嘉瑞,邢方远,许建婷,张克君
1.北京电子科技学院,北京 100070
2.西安电子科技大学,西安 710071
在复杂网络[1]领域,节点重要性排序[2]在交通规划、流行病传播[3]、舆情监控、商品推荐等领域都有着广泛的应用。研究者们已经提出了许多重要节点排序的经典算法,比如K-shell 算法[4]、HITs(hyperlink-induced topic search)算法[5]、PageRank算法[6]等。其中,K-shell算法计算复杂度低,适用于大型网络,但该算法对节点重要性的区分度不高,是一种粗粒度的重要性排序方法,对于一些特殊网络结构,如星形网络[7]等,无法发挥作用。HITs 算法开创了用不同指标同时评价网络中节点重要性的先例,但真实的网络中存在很多特殊的结构,如内部链接十分紧密的社团结构[8],这会导致社团内的节点权威值和枢纽值相互增强,使得结果出现偏差。PageRank算法在社交网络[9]分析中也有着广泛的应用,但在实际的社交网络中,人与人之间有着十分复杂的关系,PageRank中均等的分配策略显然是不符合实际的。
针对以上算法的不足,钟林峰提出了一种基于迭代资源分配的关键节点挖掘算法(iterative resource allocation,IRA)[10],并从传播学的角度对该算法进行了改进,提出了基于节点传播属性的迭代资源分配改进算法(improved iterative resource allocation,IIRA),并取得了良好的效果。
但是无论是IRA 算法还是IIRA 算法,都需要以其他算法的中心性指标作为资源分配的依据,一定程度上依赖输入指标的准确度。在社交网络中,信息往往更容易在两个更为相似的节点之间传播,以节点中心性指标作为资源分配的依据本身并不准确且无法衡量这种相似程度,在传播过程中以节点相似度作为资源分配的依据更具有合理性。因此本文将节点的相似度作为资源分配的依据,提出了SBRA(similarity-based resource allocation)算法。除此之外,基于传播概率的IIRA算法在设计之初就存在一个假设,即只有直接相连的节点之间才会存在资源的传递。但在实际的社交网络中,影响力不仅在直接相连的节点之间传播,而且会向节点的二阶邻居节点甚至更远的邻居节点传播。针对这一问题,本文将LeaderRank 算法[11]的背景节点思想引入SBRA算法,提出了基于节点相似度和高阶资源流动的L-SBRA(LeaderRank similarity-based resource allocation)算法,解决了非直接相邻节点间的资源传播问题,使得该算法更适用于社交网络。
1 IRA算法体系
1.1 IRA算法
经典的节点重要性算法大多是基于网络拓扑结构,即基于节点的属性信息。而IRA算法认为,节点的重要性不仅与自身的属性相关,也和相邻节点的属性相关。
对于给定的无向无权网络G=(V,E),其中包含|V| =N个节点和|E| =M条边。网络G的邻接矩阵A中的元素用aij表示,如果节点vi与节点vj之间有连边,则aij=1,若节点vi与节点vj之间没有连边,则aij=0。IRA算法公式如下:

其中,IRA 值用来衡量每个节点的重要程度,IRAi(t)表示第t个时间步节点vi的IRA 值,Γ(i)表示节点vi的邻居节点集,θi表示节点vi的一个具体的资源值,可以将K-shell、度中心性(degree centrality,DC)[12]、特征向量中心性(eigenvector centrality,EC)[13]、接近中心性(closeness centrality,CC)[14]等指标作为输入,α为可调节中心性值的权重。
IRA算法大致流程为:首先将所有节点的IRA 值都初始化为1,然后按照式(1)迭代更新IRA 值直至其稳定,最后得到的资源值就代表了各节点的重要程度。
IRA算法融合了节点自身属性和邻居节点属性,文献[10]证明,相比其他算法,IRA算法在大部分网络中准确度都有不同程度的提升,并且得到了更加精确的排序结果。此外,在真实网络中,随着参数α的增大,IRA算法得出的准确率先缓慢上升然后急剧下降,这意味着随着参数α的增大,IRA算法得出的节点重要性程度排名的准确性是逐渐下降的,因此后续文章默认该值为1。
1.2 IIRA算法
IRA 算法同时考虑节点自身属性和邻居节点属性的影响,提高了重要节点排序的准确性,但IRA 算法在对叶子节点的重要性排序中往往表现较差。这是由于在资源分配的过程中,网络的局域现象干扰了算法的准确性,未考虑节点的传播属性可能会对资源分配的结果产生影响。因此,文献[10]引入节点的传播概率,提出了改进的资源分配算法IIRA。在IIRA算法的资源分配过程中,节点获得的资源值不仅与节点自身和邻居节点的属性信息有关,还受到传播概率和邻居节点数目的影响。

对于给定的无向无权网络G=(V,E),IIRA 算法公式如下:其中,IIRA 值用来衡量每个节点的重要程度,IIRAi(t)表示第t个时间步节点vi的IIRA 值。式(2)中除ψi外各符号与IRA算法中相同。ψi表示节点所受到的传播属性的影响,具体含义为:

其中,β为传播概率;di为节点vi的度,定义为:

IIRA算法大致流程为:首先将所有节点的IIRA 值都初始化为1,然后按照式(2)迭代更新IIRA 值直至其稳定,最后得到的资源值就代表了各节点的重要程度。改进后的IIRA算法准确性比IRA算法有了进一步的提高。
2 基于节点相似度的SBRA算法
IRA算法体系可以应用于许多中心性算法,并提高这些中心性算法的性能。但这样会使得排序的结果很大程度上依赖于输入的中心性指标,只能有限地提升算法的准确度,难以突破这些中心性指标的局限。
在实际的社交网络中,人们往往有着复杂的关系。从传播学的角度来说,消息在不同节点之间的传播能力是不同的。例如在消息网络中,消息往往更容易在有着相同兴趣爱好的小圈子里快速传播,换句话说,它们更为相似。在社交网络中,节点之间的相似程度也可以用来刻画节点之间的消息传播效率。传统的中心性指标是无法衡量这种相似程度的,也是不够准确的,因此提出一种新的指标来替代原有的中心性指标作为资源分配算法的输入很有必要。正是基于上述原因提出SBRA算法,用节点之间的相似性指标代替中心性作为IIRA算法的输入,通过节点之间相似性的比例来分配资源,使得算法更适用于社交网络。
2.1 算法思想
SBRA 算法的核心思想是计算节点之间的余弦相似度,并根据节点间的相似性指标占比作为资源分配的依据,进行迭代资源分配,最后稳定后的资源值就是节点的重要程度。
2.2 算法描述
对于给定的无向无权网络G=(V,E),在迭代开始前,将节点的资源值全部初始化为1,使用Node2vec[15]模型将网络节点表示成向量形式,并根据向量的余弦相似度得出相似性矩阵M。相似性矩阵M中的元素mij的计算方法如下:
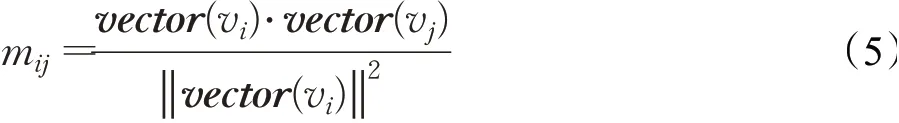
其中,mij为节点vi与节点vj的余弦相似度,vector(vi)表示节点vi的向量,‖ ‖vector(vi) 表示节点vi的向量模长,余弦相似度的范围为[-1,1]。在资源分配的过程中,要以相似度的占比来分配资源,其中的零值和负值的相似度是无法参与计算的,在实际的社交网络中也是不合乎逻辑的。因此对相似度的值进行修正,将余弦相似度的值整体加1 并乘上0.5,使节点的相似度修正到[0,1]的区间,得到修正后的相似性矩阵S,既便于计算,又符合通常的认知。矩阵S中的元素sij为:

其中,sij为节点vi与节点vj修正后的余弦相似度。
初始化完成后,开始资源迭代分配。在每轮的迭代过程中,每个节点的资源值更新为其所有相邻节点为其分配的资源值总和,而资源分配的依据就是节点间的相似性指标占比。用Ii(t)表示第t轮资源迭代节点vi的资源值,则每轮迭代节点vi获得的资源可以表示为:

除sij外各符号与IRA算法体系一致。

可以进一步写成矩阵形式:矩阵W中的元素wij为:

可以将资源矩阵W看作一个对角阵D左乘矩阵T得到的矩阵,式(8)则可以改写为:
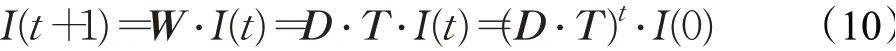
其中对角阵D可表示为:

可知tij≥0 且∑itij=1,根据圆盘定理[16],当t趋于无穷时,Tt将收敛于一个常数矩阵,而矩阵左乘一个对角阵只会使其行乘上一个倍数,又由于矩阵D中的元素取值均在(0,1]区间,因此资源值的变化量会无限趋近于零值,也就是说存在一个足够小的ε,且ε >0,当I(t)在t趋于无穷时收敛,满足 |I(t)-I(t-1)|<ε,经过若干轮迭代后,资源值一定会达到稳定状态。
具体来看,SBRA算法的过程如下:
(1)计算出资源矩阵W并初始化资源值I(0)=(1,1,…,1)T。
(2)按I(t+1)=W·I(t)或I(t)=Wt·I(0)的方式更新第t轮迭代节点的资源值。
(3)重复步骤(2),直到所有节点的资源值稳定,即满足 |I(t)-I(t-1)|<ε,令ε=10-6。
以图1中的网络a来详细说明SBRA算法。其中有5个节点和5条边,在初始阶段,将其资源值全部设为1,即I(0)=(1,1,…,1)T,经过建模可以得到节点的向量表示,将修正的节点之间的余弦相似度作为资源分配的依据,假设传播概率β为0.8,则资源分配矩阵W为:

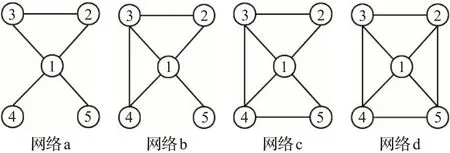
图1 具有5个节点的网络示例Fig.1 Network examples with 5 nodes
因为SBRA算法中对角阵的存在,节点资源值会随着迭代不断变少,所以将每轮迭代后的资源值总量重新等比放大到初始化时的资源总量。如图2所示,可以看到经过迭代,网络a中的每个节点的资源变化值最终趋于0,表示资源值达到稳定状态。

图2 SBRA算法下网络a节点资源变化值Fig.2 Node resource change value in Network a with SBRA algorithm
在网络a的基础上得到网络b、网络c、网络d。同样设置修正的余弦相似度作为资源分配依据,并将资源迭代后的结果放缩到合适的区间,可以得出网络节点最终的资源值。如表1所示,随着节点2、3、4节点度的增大,节点1在网络中的重要性比重逐渐减弱,这样的结果也是符合通常认知的。
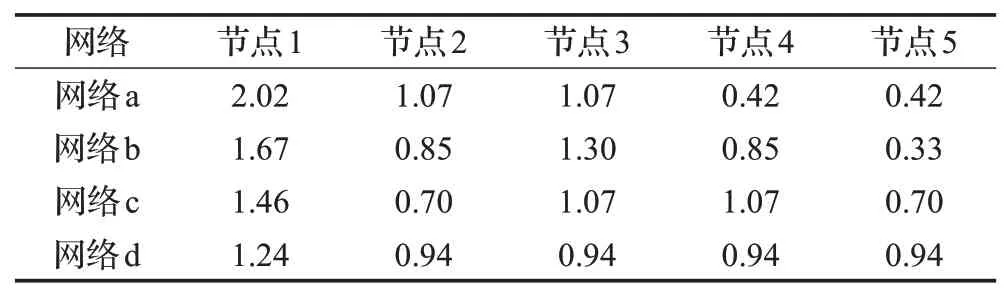
表1 SBRA算法在图1中网络各节点迭代稳定的资源值Table 1 Iterative stable resource value of each node of networks in Fig.1 with SBRA algorithm
3 基于节点相似度和高阶流动的L-SBRA算法
IIRA 算法在设计之初就存在一个假设,即只有直接相连的节点之间才会存在资源的传递。但无论网络中的节点是否直接相连,其影响力的传播都是存在的,只是影响力的传播距离越远,对节点影响就越小。资源分配的过程也应该考虑到非直接相连的节点的资源流动情况。因此将LeaderRank 算法的背景节点思想引入SBRA算法,提出了L-SBRA算法。
3.1 算法思想
L-SBRA算法就是在SBRA算法的基础上在网络中加入一个背景节点。首先将背景节点和原网络中的每个节点建立连边,然后通过连边关系将相邻节点分配的资源值迭代更新到每个节点上,直到每个节点的资源值都达到稳定状态,再将背景节点的资源值按照输入指标的占比分配给原网络中的每个节点,此时节点的资源值大小即可作为节点重要性排序的指标。
3.2 算法描述
对于给定的无权无向网络G=(V,E),加入背景节点vb形成新的网络Ge,网络Ge的邻接矩阵U中的元素用uij表示,若网络Ge中的节点vi和vj有连边则uij=1,反之若没有连边则uij=0。并将新的网络除背景节点外的资源值全部初始化为1,背景节点的资源值初始化为0。若用Ie表示网络Ge节点的资源值,则Ie=[1,1,…,1,0]T。
对于节点相似性来说,在加入背景节点后,由于背景节点与原网络中的所有节点都相连,在建模时从每个节点随机游走到该节点的概率都很大,即背景节点和所有节点的相似度都很高,这就会导致在资源迭代时大量的资源流动到背景节点。这样的结果违背了设计算法的初衷,即希望只有少量的资源通过背景节点,用以表示资源在高阶邻居节点间的流动。因此用原网络G中所有节点对之间相似度的平均值sˉ作为背景节点与其余各节点的相似度。可得相似性矩阵S′,其中矩阵中元素s′ij为:

初始化完成后,开始进行资源迭代。用Iei(t)表示第t轮迭代网络Ge中的节点vi的资源值,那么每轮迭代网络Ge的节点资源值可以表示为:
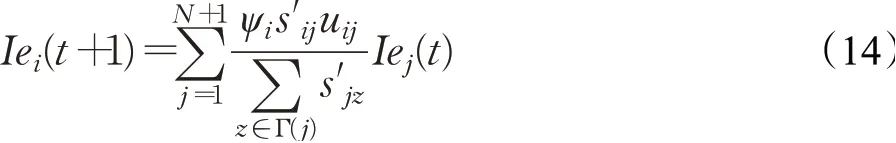
可以进一步写成矩阵形式:
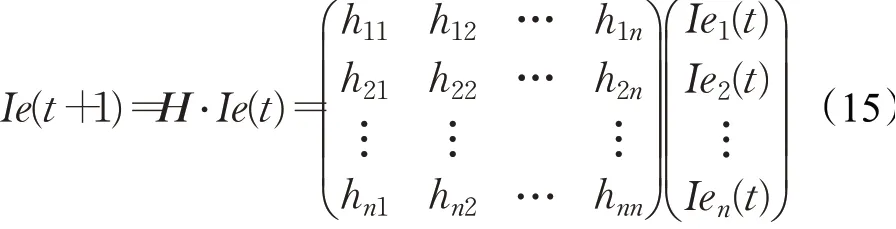
矩阵H中的元素hij为:

同样可以证明,当迭代次数t足够大时,节点的资源值会趋于稳定。最后,将背景节点的资源值按照各节点与背景节点修正的余弦相似度比重分给原网络中的各个节点,便可以计算出节点vi的最终资源值:

其中,sib指网络Ge中节点vi与背景节点vb修正后的余弦相似度。
具体来看,L-SBRA算法的过程如下:
(1)网络G中加入背景节点vb形成网络Ge,计算出资源矩阵H并初始化资源值Ie=[1,1,…,1,0]T,其中背景节点的资源值为0。
(2)按Ie(t+1)=H·Ie(t)或Ie(t)=Ht·Ie(0)的方式更新第t轮迭代节点的资源值。
(3)重复步骤(2),直到所有节点的资源值稳定,即满足 |Ie(t)-Ie(t-1)|<ε,令ε=10-6。
(4)将背景节点的资源值按照各节点与背景节点修正的余弦相似度比重分给其他节点,得到各节点的最终资源值Ii(t)。
同样以图1 中的网络a 来详细说明L-SBRA 算法。在初始阶段,加入背景节点并将资源值初始化Ie(0)=(1,1,…,1,0)T,假设传播概率β为0.8,则资源分配矩阵H为:
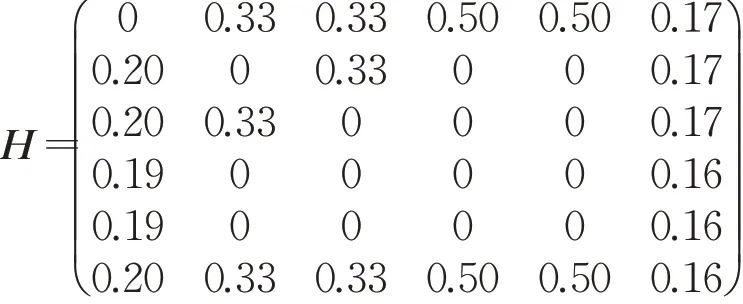
因为节点的资源值最终会收敛到一个稳定的状态,所以将每轮迭代后的资源值总量重新等比放大到初始化时的资源总量。如图3 所示,可以看到经过迭代,网络a 中的每个节点的资源变化值最终趋于0,资源值达到稳定状态。

图3 L-SBRA算法下网络a节点资源变化值Fig.3 Node resource change value in Network a with L-SBRA algorithm
同样对图1的4个网络设置修正的余弦相似度值作为算法的输入,假设传播概率β为0.8,并将资源迭代后的结果放缩到合适的区间,可以得出网络节点最终的资源值。如表2所示,随着网络节点2、3、4连边的增多,节点1 重要性不断降低,而连边变化后节点3、4、5 的重要性始终未超过节点1,在网络b 中节点3 的连边多于节点2和4,因此重要性高于节点2和4,与预期一致。

表2 L-SBRA算法在图1中网络各节点迭代稳定的资源值Table 2 Iterative stable resource value of each node of networks in Fig.1 with L-SBRA algorithm
4 实验与分析
本文设计了对比实验来展示和分析IIRA、SBRA及L-SBRA算法的有效性和优越性。
4.1 实验模型与数据集
实验采用基于传播动力学的SIR模型[17]作为评价标准,以某一节点在一定时间感染的节点数来衡量该节点在网络中的重要程度。为了刻画节点重要性排序算法的准确度,采用不精确函数(Inaccu function)和Kendall系数[18]来表示排序结果和节点真实影响力之间的关系。
不精确函数是通过计算关键节点挖掘算法得出来的关键性排名里比较靠前的关键节点的平均传播能力,进而判定挖掘算法准确性的函数,其计算方法为:

其中,εalg(p)表示通过重要性排序算法alg 得出的网络中重要程度排前pN个节点的影响力与网络中真实传播能力排前pN个节点的影响力区别。Malg(p)表示算法得出的前pN个节点在一定的时间步感染的节点数,Meff(p)表示网络中真实传播能力排前pN个节点的在相同时间步感染的节点数。这里的p为选取网络中节点的比例,0<p <1,N为网络总节点数。若Malg(p)与Meff(p)越接近,则不精确函数εalg(p)值越小,表示算法的结果精确度越高。
Kendall 系数τ可以用来表示两个序列之间的相关程度,用这个指标来评价重要性排序算法得到的结果与节点的真实影响力之间的相关性,其具体计算方法为:
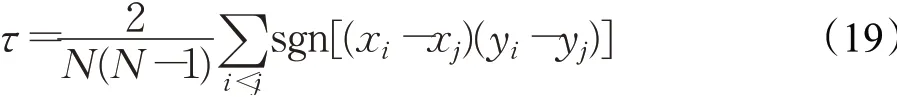
其中,N为网络节点总数,xi表示节点vi的真实影响力,即SIR模型模拟的影响力,yi表示排序算法计算出的节点vi影响力。sgn(x)为符号函数,当x >0,时sgn(x)=1,当x <0 时,sgn(x)=-1,当x=0 时,sgn(x)=0。算法准确性越高则τ值越大。
为了验证算法的有效性和优越性,本文数据集采用了US Airline网络、Email网络和Hamster用户网络。三个网络均为无权无向网络,网络的基本参数如表3 所示。其中N为网络节点数,M为网络边数,<k >为网络平均度,r为网络的同配系数,C为网络的平均聚集系数。
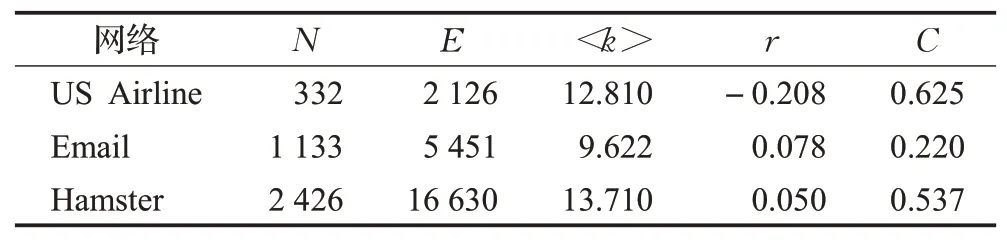
表3 网络数据集参数Table 3 Network dataset parameters
4.2 SBRA与IIRA对比实验
设置SIR模型的传播率为0.2,恢复率为0.1,分别以DC、EC、CC、K-shell值作为IIRA算法的输入,两种算法中节点间的传播概率β取0.8,使用Node2vec算法来对网络结构建模。经过迭代可以得到两个算法在各网络中的不精确函数和Kendall 系数。
如图4、图5所示,在US Airline网络中,SBRA算法表现和以DC、EC、CC中心性指标为输入的IIRA算法精确度相当,明显优于以K-shell指标为输入的IIRA算法。
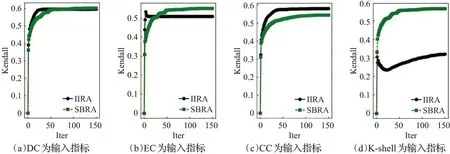
图4 US Airline数据集不同输入指标的Kendall系数Fig.4 Kendall coefficients of different input indicators in US Airline dataset
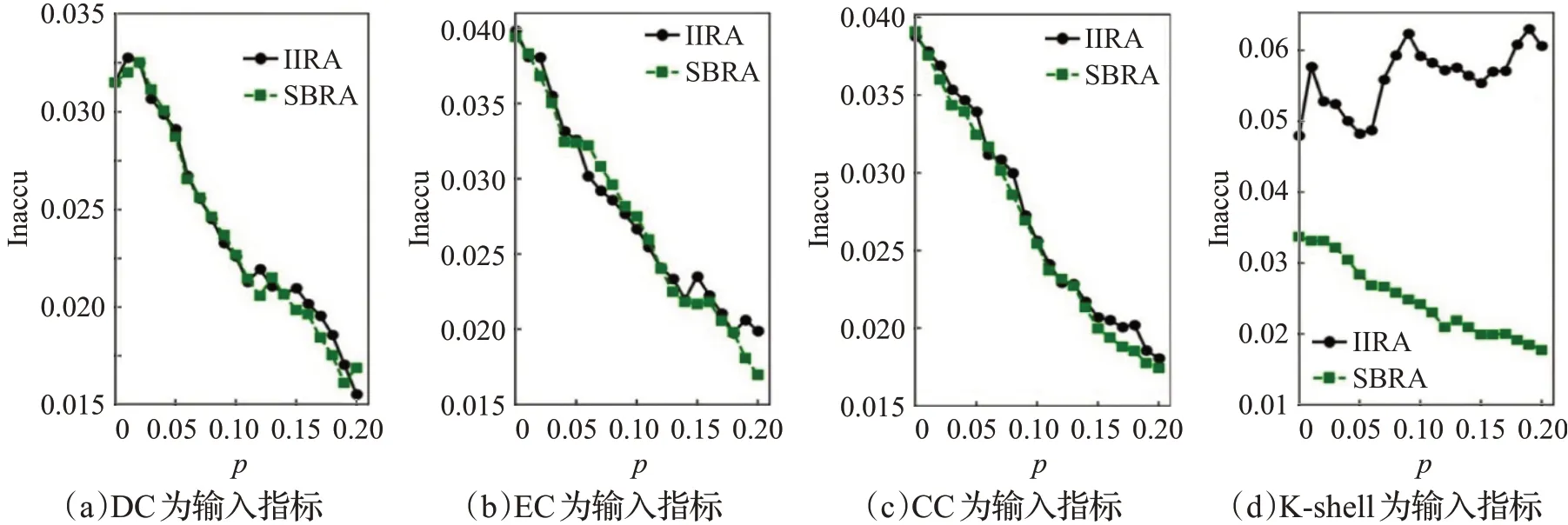
图5 US Airline数据集不同输入指标的不精确函数Fig.5 Inaccu function of different input indicators in US Airline dataset
如图6、图7所示,在Email网络中,两种算法的表现和在US Airline中相似,SBRA算法和以DC、EC、CC中心性指标为输入的IIRA 算法精确度相当,显著优于以K-shell指标为输入的IIRA算法。
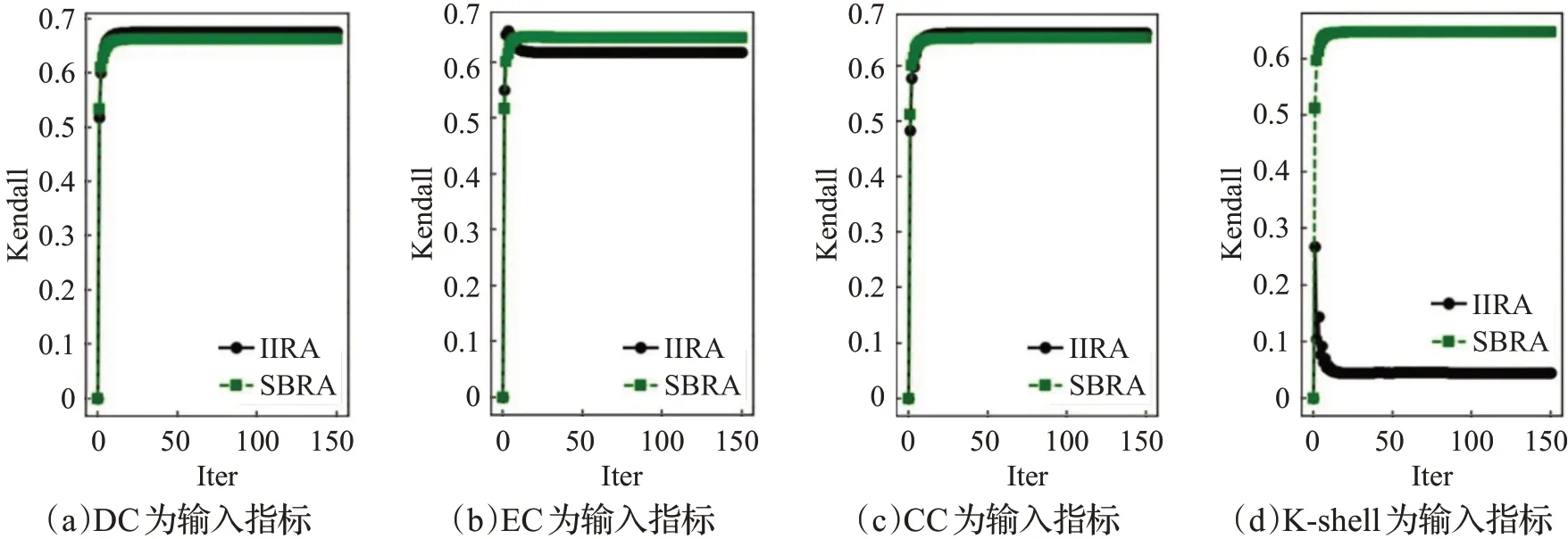
图6 Email数据集不同输入指标的Kendall系数Fig.6 Kendall coefficients of different input indicators in Email dataset

图7 Email数据集不同输入指标的不精确函数Fig.7 Inaccu function of different input indicators in Email dataset
在图4 到图7 中,无论是以哪种中心性指标作为输入,IIRA 算法和SBRA 算法在迭代100 次前的Kendall系数都可以趋于稳定。在US Airline网络和Email网络中以DC、EC 和CC 中心性指标作为输入的IIRA 算法Kendall 系数和SBRA 算法稳定后的Kendall 系数都十分接近,不精确函数也基本重合。两种算法的Kendall系数接近说明在这两个网络中,两种算法的精确度基本一致,基本重合的不精确函数说明导致出现结果差异的节点影响力十分接近,它们之间的影响力差别基本可以忽略不计。以K-shell值作为输入的IIRA算法中,SBRA算法明显结果更优。出现这一现象的原因在于IIRA算法精度依赖于输入的中心性指标,而K-shell 值本身并不精确。
如图8、图9所示,在Hamster网络中,SBRA算法在第25次迭代之后就已稳定,其精确度均高于IIRA算法,明显优于以EC 中心性指标和以K-shell 指标为输入的IIRA 算法。SBRA 算法和以DC 中心性指标为输入的IIRA 算法在影响力排前7%的节点精确度相当,在超过7%节点后显著优于IIRA 算法,和以CC 中心性指标为输入的IIRA 算法在影响力排前14%的节点精确度相当,在超过14%的节点以后明显优于IIRA 算法。可以看到,SBRA算法不仅收敛速度更快,而且精度更高、更稳定。

图8 Hamster数据集不同输入指标的Kendall系数Fig.8 Kendall coefficients of different input indicators in Hamster dataset
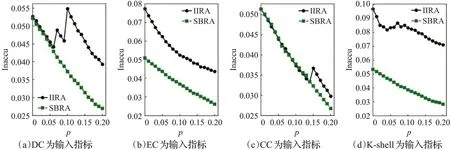
图9 Hamster数据集不同输入指标的不精确函数Fig.9 Inaccu function of different input indicators in Hamster dataset
通过IIRA 算法和SBRA 算法的对比实验可以看出,在三个不同网络中两种算法的表现并不相同。IIRA算法的精度很大程度上受输入的中心性指标影响。如图10、图11所示,将SBRA算法迭代稳定后的资源值作为IIRA算法的输入重新迭代,算法的精度下降,可以说明SBRA 算法已经接近了IRA 算法体系的精度上限。两种算法在Hamster网络中SBRA的表现更好,已经可以说明以节点相似度作为输入要比以中心性指标作为输入进行资源迭代更加合理。在US Airline网络和Email网络中两种算法精度相当,是由于这两个网络的节点数较少,中心性指标的误差不至于影响到节点的重要性排序情况,因此两种算法都能准确地识别到关键节点。

图10 IIRA重新迭代SBRA稳定后资源的三个网络的Kendall系数Fig.10 Kendall coefficients of three networks when IIRA re-iterates resources after SBRA stabilization

图11 IIRA重新迭代SBRA稳定后资源的三个网络的不精确函数Fig.11 Inaccu function of three networks when IIRA re-iterates resources after SBRA stabilization
通过对比实验可以得出,在节点数量较多的情况下SBRA 算法的精度要高于IIRA 算法。在时间方面,以CC 中心性指标为输入的IIRA 算法虽然有一定的精确度,但由于要计算CC中心性指标,算法的复杂度随着网络规模的增大呈指数级上升,对于大型网络来说这样的计算成本是不可接受的,相对而言SBRA算法计算复杂度要小得多。在算力成本不断下降的今天,SBRA算法的复杂度仍然是可以承担得起的。但这并不说明在较少节点情况下SBRA 算法是没有意义的。由于IIRA 算法有多种输入,并不能确定用哪种输入可以得到最准确的排序结果。而SBRA 算法在小型网络中虽然排序精度并不会提升,但其排序结果与IIRA 算法最精确的排序结果相当,免去了选择输入指标的麻烦。因此可以得出SBRA算法优于IIRA算法的结论。
4.3 L-SBRA与SBRA对比实验
设置SIR模型的传播率为0.2,恢复率为0.1,L-SBRA算法和SBRA 算法中节点间的传播概率β取0.8,使用Node2vec 算法来对网络结构建模。经过迭代可以得到两种算法在各网络之中的不精确函数和Kendall 系数,如图12、图13所示。

图12 L-SBRA算法与SBRA算法在三个网络中的Kendall系数Fig.12 Kendall coefficients of L-SBRA algorithm and SBRA algorithm in three networks

图13 L-SBRA算法与SBRA算法在三个网络中的不精确函数Fig.13 Inaccu functions of L-SBRA algorithm and SBRA algorithm in three networks
在三个网络中,L-SBRA算法均在第25次迭代之前趋于稳定,收敛速度均比SBRA 算法快,算法收敛速度加快是由于背景节点的出现使得网络中的连边数显著增多,从而加快了资源流动的速度。在US Airline网络和Email 网络中,SBRA 算法和L-SBRA 算法的精确度基本相当。在Hamster 网络中,在选取节点数量超过网络节点总数的14%时,L-SBRA 算法精度也有一定的提高。结合算法在三个网络中的表现同样可以得出,算法可以同时提高收敛速度和准确度。在US Airline 网络和Email网络上算法精度未提高,是因为这两个网络规模较小,算法的精度差,不足以影响节点的排序结果。
通过上述对比实验,可以发现在小型数据集上SBRA算法和L-SBRA 算法都能接近IRA 算法框架的精度上限,而L-SBRA 算法收敛速度更快;在大型数据集上,L-SBRA 算法收敛速度不仅更快,而且准确率也更高。由此可以得出结论,L-SBRA算法要优于SBRA算法。
5 结束语
本文分析了IIRA 算法的不足之处,对IIRA 算法进行改进,使用节点相似性指标替换掉原算法中的中心性指标作为算法的输入,提出了SBRA算法。并且在SBRA算法的基础上,引入了LeaderRank算法中背景节点的思想,提出了L-SBRA算法。这两种改进算法考虑了非直接相连节点间的传播情况,更加符合社交网络的实际情况,也更加合理。通过设置以四种中心性指标为输入的IIRA算法与SBRA算法的对比实验,展示了在三个真实网络中两种算法的表现,并分析出现结果差异的原因,证明了相似性作为算法输入的合理性。设置L-SBRA算法和SBRA算法的对比实验,展示了在三个不同真实网络中两种算法的表现,并分析了两种算法精度和收敛速度出现不同的原因,证明了L-SBRA算法的优越性。
本文网络建模部分使用了Node2vec 模型,而该模型产生随机游走序列时只考虑了连接关系,而在实际的社交网络中,节点的属性信息也应该对该随机游走序列产生一定影响。另外,本文研究的对象为静态无权无向网络,而在真实的社交网络中,还存在更为复杂的结构,并且网络的拓扑结构也是变化的。因此在未来的研究中,可以考虑修改随机游走序列的产生规则,让生成的随机游走序列包含节点的属性信息,以及考虑到网络结构的动态变化,使得算法更加适用于真实的社交网络。
