基于超单元法的动力电池舱结构优化设计

董 廷

(金龙联合汽车工业(苏州)有限公司， 江苏 苏州 215000)

在全承载式电动客车中，动力电池舱是其关键结构件，不仅起到安装固定动力电池的作用，而且影响到整车的承载。通常需要对动力电池舱结构进行轻量化优化设计。在客车车身结构优化设计中常用的方法为拓扑优化和尺寸优化。在进行局部结构的优化设计时，如果使用整车有限元模型会浪费大量的计算资源。通过超单元方法将需要进行优化设计的局部结构划分成独立的子结构，将其余部分通过超单元理论缩聚为独立的矩阵施加到要优化的子结构中，可以大大提高求解速度。

1 超单元定义

在动力电池舱局部结构的拓扑优化和尺寸优化中，均可通过力学分析进行优化求解(本文仅涉及静力学)。因此，只需提取超单元部分缩聚后的刚度矩阵和载荷矩阵即可。本文使用GUYAN静力变换超单元缩聚法对超单元部分进行静态矩阵缩聚，此方法运算比较简单，对静力学问题求解精度较高。

1.1 力学分析超单元基本理论

有限元分析的基本力学方程为：

=

(1)

式中：为结构刚度矩阵；为节点位移向量矩阵；为载荷向量矩阵。

将整个有限元模型划分为两个部分，一部分为超单元，另一部分为待求解子结构。分界处的节点为两个部分的公共节点，节点编号相同。对于超单元部分，式(1)中的、、分解为内部节点自由度集(下标ο)和边界节点自由度集(下标α)，则式(1)可以变形为：

(2)

由式(2)可以得到分界处节点的求解方程：

(3)

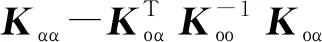
对于待求解子结构，设其结构刚度矩阵、节点位移向量矩阵和载荷向量矩阵分别为′、′、′,同样可得到：

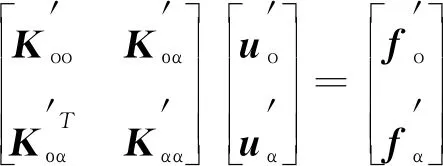
(4)

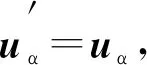
(5)

1.2 超单元结构划分

首先建立如图1所示的整车有限元模型，并设置水平弯曲、制动、转向、左前轮悬空扭转(扭转1)、右后轮悬空扭转(扭转2)5个典型工况。

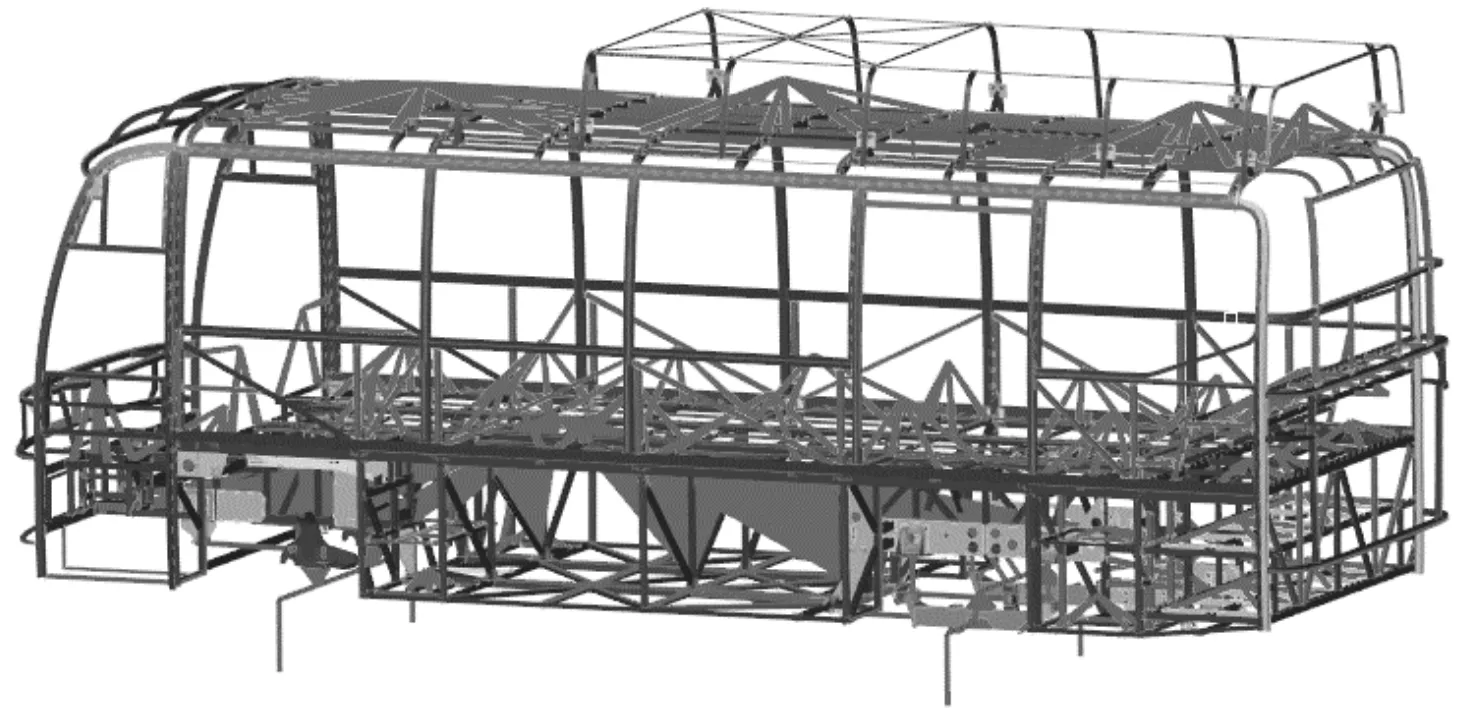
图1 整车有限元模型

超单元和剩余待求解子结构连接节点的多少直接决定了超单元缩聚后刚度矩阵和载荷矩阵的大小，也直接影响子结构的求解速度。因此需选择合理的分割截面，尽量减少超单元和剩余待求解子结构的连接节点数量。本文将分界截面选在动力电池舱型材的横截面上，最终分割出的动力电池舱待求解子结构如图2所示。整车有限元模型的其余部分作为超单元结构，进行超单元矩阵缩聚。

图2 电池舱待求解子结构

1.3 电池舱待求解子结构模型求解验证

使用HyperWorks OptiStruct求解器的GUYAN静力变换超单元缩聚法对超单元部分进行静态矩阵缩聚，得到缩聚后的刚度矩阵和载荷矩阵，将其组装到电池舱待求解子结构中求解。5个典型工况下电池舱子结构对应的最大应力值和整车有限元模型完整求解对应的电池舱中最大应力值见表1。

表1 子结构和完整模型求解最大应力对比

对比表1中的数据，证明采用超单元进行求解是有效的。

在相同的计算机配置下，采用完整模型和超单元进行分析所需要的时间分别为12.75 min和1.63 min。在进行优化设计时，需要进行多次分析以搜索最优解，因而通过超单元求解效率优势更明显。

2 结构优化设计

动力电池舱子结构为采用矩形管搭建的桁架式结构。最上一层安装电器件，固定点较多，拓扑优化空间较小；下面两层为结构相同的动力电池托架，固定点较少，拓扑优化空间较大。因此，先对下面两层托架进行拓扑优化，再对动力电池舱所有的矩形管进行壁厚尺寸优化。

2.1 电池托架拓扑优化

拓扑优化采用OptiStruct求解器的SIMP变密度插值算法。电池托架除固定支架外的区域作为拓扑优化空间，在拓扑优化空间中放置平板，平板采用壳单元，拓扑优化空间中壳单元的单元密度为设计变量。约束条件为体积分数不大于30%和前述5个工况的最大应力不大于200 MPa。目标函数为前述5个工况的加权柔度最小，弯曲工况的权重系数为50%，其余4个工况的权重系数均为12.5%。为提高制造工艺性，约束两个电池托架(图2中电池安装面B和C)的设计变量区域结构相同，同时约束电池托架的拓扑结构关于车辆纵向对称面对称。

经过12次迭代得到电池托架(图2中电池安装面B和C)的拓扑优化结果如图3所示。根据以上拓扑优化结果和周边布置进行具体的结构优化设计。优化前后的电池托架下面两层的结构如图4所示。

图3 电池托架下面两层的拓扑优化结果

(a) 优化前电池托架下面两层的结构

2.2 电池舱骨架尺寸优化

使用图4(b)的结构替换原结构(图2中电池安装面B和C)，新的电池舱子结构骨架(包含电器安装面A)共包含矩形管84件(原结构68件)，为方便制作，根据型材的位置和功能对其进行分类，最终分为17类。将该17类矩形管的壁厚定义为17个设计变量进行壁厚的尺寸优化，壁厚的最大值设置为3 mm。约束条件为所有工况的最大应力不大于原结构的最大应力200 MPa，目标函数为整体质量最小。

经过20次迭代得到的新电池舱子结构骨架矩形管的壁厚分布如图5所示。

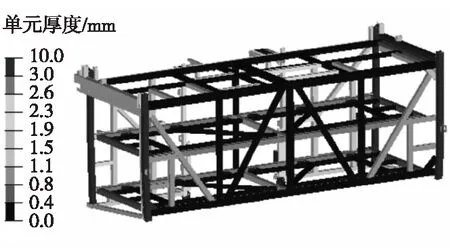
图5 电池舱骨架矩形管壁厚分布图

根据壁厚优化结果对其中有关的矩形管壁厚作如下调整：

1) 电池托架左右贯通横梁为主要的承力部件，保持其壁厚2.5 mm不变；电池托架中心梁和两侧纵梁为次要承力部件，将其壁厚由2.5 mm改为2.0 mm；其余矩形管壁厚设置为1.5 mm。

2) 最上一层周圈方管壁厚由2.5 mm调整为2.0 mm，中间方管壁厚由2.5 mm调整为1.5 mm。

3) 后截面两侧斜撑为主要承力部件，厚度由1.5 mm调整为2.0 mm；中心梁壁厚由2.5 mm调整为2.0 mm；上下横梁壁厚由2.5 mm调整为2.0 mm；其余斜撑保持壁厚1.5 mm不变。

2.3 结构优化效果

按以上拓扑优化的结果和调整后的矩形管壁厚建立电池舱子结构骨架模型，再一次采用超单元法进行求解，电池舱骨架处各工况对应的最大应力见表2。优化前后整车的最大应力对比见表3。

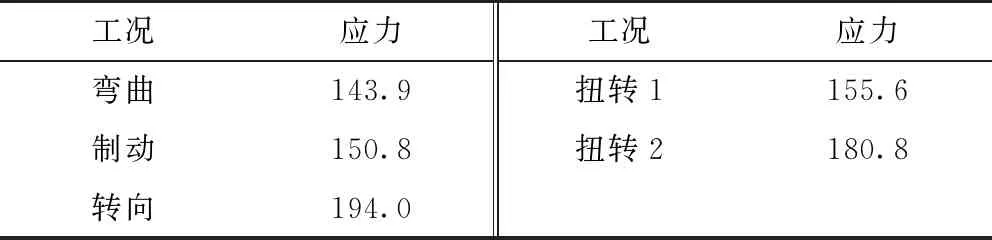
表2 优化后电池舱子结构最大应力 MPa

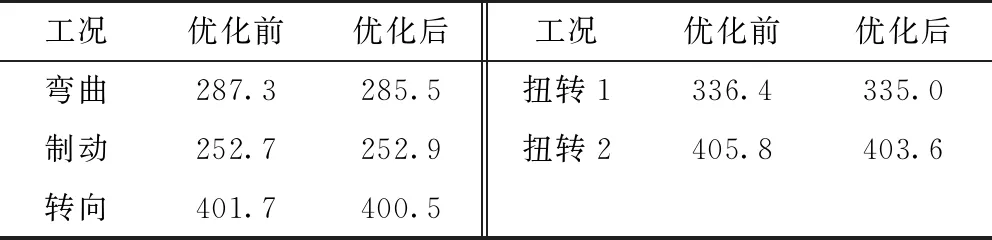
表3 优化前后整车最大应力 MPa

从表1、表2和表3可以看出，优化前后电池舱子结构骨架处最大应力和整车最大应力基本没有变化。电池舱子结构骨架优化前的质量为174 kg，优化后的质量为140 kg。

3 结束语

通过拓扑优化和尺寸优化使动力电池舱减重19.5%，且受力情况基本未变，提高了结构设计的合理性。此优化方案已在多个电动客车上得到应用。在进行优化设计时，通过超单元理论，将动力电池舱分割为单独的子结构进行求解计算，提高了计算效率。