带一字肋组合桥面板横向受力简化计算方法研究

陈同琪， 李庆华， 童精中， 徐世烺

（浙江大学高性能结构研究所，杭州 310058）

0 引言

正交异形钢桥面板结构体系复杂，受力分析方法主要为解析法和数值法两种［1］。采用传统解析方法会存在计算量大、精确程度不高等诸多问题［2］。目前比较经典的解析方法包括Pelikan-Esslinger法（简称P-E法）和H.Homberg方法（梁格法）。前者分为两个阶段计算，首先假设横肋不发生弹性变形，刚度无穷大，因而此时的纵肋受到横肋的刚性支承，可求出纵肋内力和反力；然后则计入横肋弹性变形的因素，从而对第一步骤所得弯矩进行修正。梁格法是采用等效的梁格体系模拟正交异性桥面体系，将纵横肋的刚度集中到对应的相邻梁格内，两者布置相似，在受到荷载作用时，等效梁的挠度等于加劲肋的挠度，前者的内力可近似为后者的内力［3］。

吴臻旺等［4］考虑了顶板厚度、主梁高度、横隔板间距以及吊杆纵向间距内横隔板节间数对横向应力的影响，通过大量试算，总结出桥面局部应力简化计算公式；郭增伟等［5］通过解析分析模型，提出了桥面板与U肋交接位置处横向弯曲应力的解析公式，讨论并明确了影响桥面板横向弯曲应力峰值的关键敏感影响因素，但以上研究涉及的纵向加劲肋截面形式均为闭口U肋，带开口肋正交异性桥面板横向受力相关理论研究较少。文中将对其受力模型进行理论推导，考虑受力局部性的特点，将横肋间的桥面板及纵肋体系简化为带有弹性支撑的框架体系，进而可利用结构力学中的力法推导，给出了使用纵向加劲肋抗弯刚度求解钢桥面板和纵肋交界处的最大横向弯矩的计算方法。在此基础上，对开口肋钢-UHTCC（超高韧性混凝土）组合桥横向受力进行分析，对UHTCC板进行截面刚度换算，最后利用大型通用有限元软件ABAQUS建立随机模型验证了上述理论的正确性。

1 纯钢桥面板简化计算法

由于纵横肋的存在，正交异性钢桥面板受力不连续，张士红、向泽、欧阳泽卉等［6-8］的有限元计算结果显示，在轮载作用下正交异性开口肋纯钢箱梁和组合桥面均具有明显的局部受力特性。因而，可以将受到轮载影响的部分桥面板单独取出作为分析对象。另外，考虑到受力时一字肋底部与横隔板接触位置会产生转动角度，且横隔板竖向抗弯刚度远大于桥面板的抗弯刚度，横隔板对横向桥面结构的约束可简化为铰接弹簧，此处忽略顶板受横隔板的抵抗扭转因素。因桥面受力的局部性，分析对象外的桥面竖向位移较小，但转角较大，张士红等的研究结果同样说明此点，故简化结构在横桥向与桥面的连接亦按照铰接处理。简化后的一字肋平面框架体系，如图1所示。

图1 正交异性桥面板简化平面框架体系

图1中，l为纵肋间距，I是框架截面（桥面板）的横向抗弯惯性矩，计算如下：

式中，a为实际车轮与桥面接触的顺桥向宽度；t为桥面板厚度。

K为简化后的纵向一字肋底部弹性支撑刚度。将两横隔板之间的受荷载影响的一字肋及顶板区域作为隔离体，如图2所示，可简化为间距为l、跨度为横隔板间距、抗弯刚度为EIl的简支梁，而一字肋底部弹性支撑刚度K即反映了车轮荷载作用在桥面纵向不同位置处时顶板挠度的不同，因此可通过求解单位荷载作用在简支梁时的挠度来表示弹簧支撑刚度。单位力作用在简支梁上任一位置处时，沿着竖向力的方向引起的竖向位移即为弹性支座的柔度系数f，根据单位力作用在简支梁上的挠度公式［9］，一字肋底部弹性支撑刚度K计算公式：

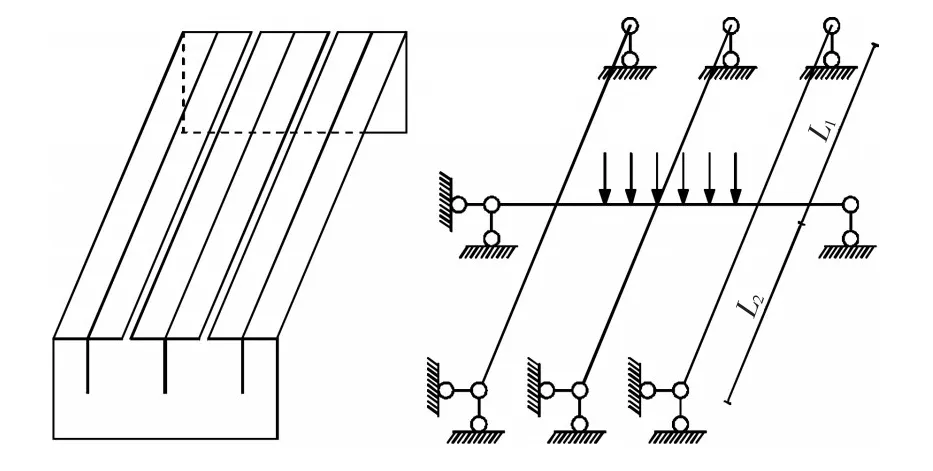
图2 纵向一字肋底部弹性支撑刚度K计算图示

式中，L为横隔板间距，Il为单个一字肋的纵向抗弯惯性矩，L1和L2分别为车轮荷载中心位置到相邻两横隔板之间的顺桥向距离。

q为等效均布荷载，它所引起的正交异性桥面板内力与原车轮荷载相似。根据P-E法和梁格法的计算原理，由于纵横肋的结构形式不同，桥面板在纵向和横向具有不等的刚度。假设荷载按照纵横肋各自具有的刚度所分配，则可近似认为桥面板长宽比约正比于荷载沿桥面横向传递的比例，即桥面板长度越长，荷载被纵肋分担的越多，沿桥面横向分配也就越多。由公式表示：

式中，Pt为荷载沿横桥向分配值，P为实际的荷载值，La为轮载横桥向的影响宽度。横桥向的分配荷载Pt仍为集中力，为便于分析，可近似认为它在实际车轮与桥面接触的横桥向宽度b内均匀分布，则等效均布荷载q由下式求得：

根据有限元结果和朱忠等［10］的研究表明，车轮荷载作用下，La近似分别为4l（工况1作用）和5l（工况2作用）。

为便于解析，同时根据前人文献研究，文中选取两种典型工况进行分析，考虑结构对称性后的模型如图3所示。

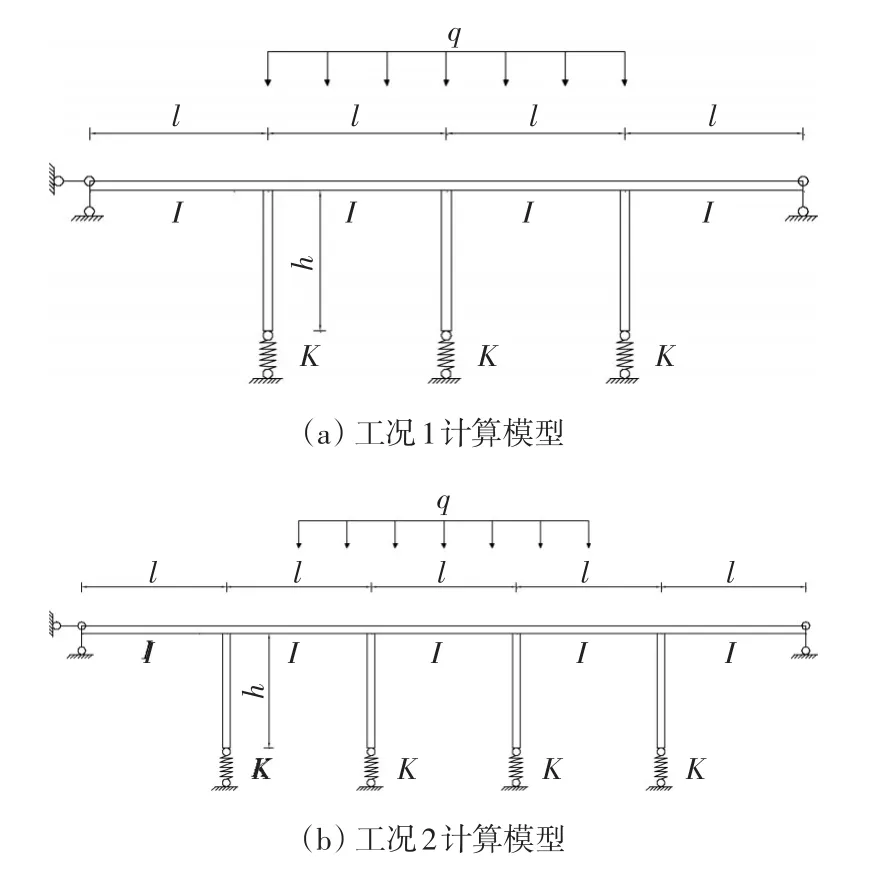
图3 横向受力计算简化模型

下面推导两种工况作用下桥面板与一字肋交界处的横桥向最大弯矩。限于篇幅，此处仅给出工况1作用下一字肋与桥面板交界处的横桥向最大弯矩推导过程，工况2推导过程类似，直接给出公式。采用结构力学中的力法［11］计算，工况1作用下模型取对称结构后的基本体系如图4所示，有3个基本未知量，X2不产生弯矩，不需考虑在内。工况1所列力法方程如下：

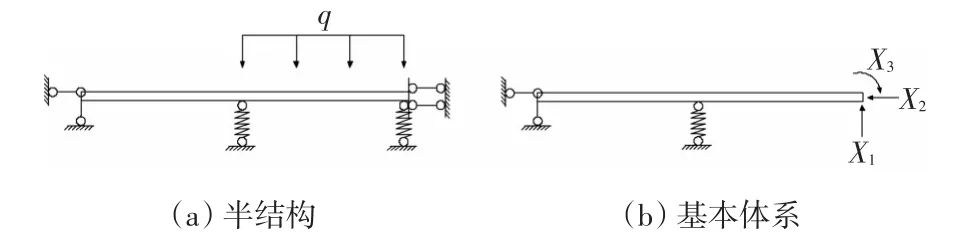
图4 工况1计算过程

由叠加原理，求得平面框架结构不同位置处的内力M：

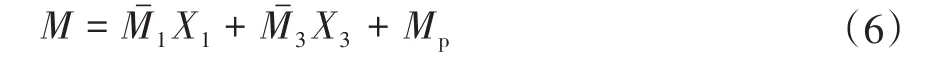
由式（5）和式（6），可得工况1作用下，一字肋与桥面板交界处的横桥向最大弯矩：

2 简化方法正确性验证

由于正交异性钢桥面板受力的局部性特点，同时为保证模型具备足够的长宽比，利用ABAQUS有限元软件随机建立含有4块横隔板的一字肋正交异性桥面板节段模型（模型一）。采用实体单元计算量较大，考虑到桥面板结构材质均匀的特点，采用三维四节点四边形有限薄膜应变线性减缩积分壳单元壳单元（S4R）对钢桥面板和加劲肋进行建模，其优点在于性能稳定，适用范围广，模型中的正交异性钢桥面板是由顶板、纵肋和横隔板合并（Merge）而成。模型一宽6.8m，长9.2m，横隔板厚度、间距分别为16mm、2.9m。桥面板厚度为16mm，一字肋厚度、高度、间距分别为16、240、30mm。采用结构化网格生成技术，在局部轮载影响区域范围内，桥面板的网格尺寸设定为10mm，其他区域设置为25mm。钢材弹性模量取210GPa，采用理想弹塑性模型，钢材为Q355钢，fy=355MPa，Es=2.06×105MPa。共设置两个分析步，分别为初始分析步和静态通用分析步，前者加边界条件和自重荷载，后者施加车辆荷载。创建场输出变量和历史变量，其中包括应力应变、截面弯矩、节点反力等。采用ABAQUS/Standard求解器进行求解。桥面板和横隔板顺桥向两端约束所有自由度，横隔板横桥向下翼缘约束沿x方向自由度，所建立的有限元模型，如图5所示。

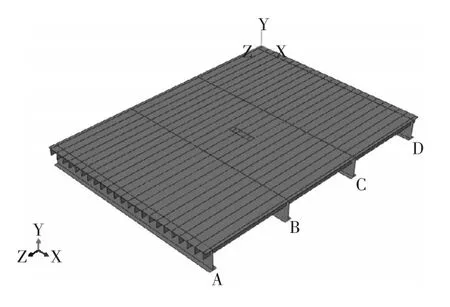
图5 一字肋正交异性桥面板节段模型（模型1）

加载所用荷载采用JTGD 64-2015《公路钢结构桥梁设计规范》［12］，中的疲劳车辆荷载Ⅲ，单轮加载，轮载接地面积为横桥向长600mm，纵桥向长200mm。通过力控制加载的方式，大小为60kN，均布于加载区域。将此荷载施加于B、C横隔板之间桥面板跨中位置，利用上文中的简化计算法和有限元模型分别求得两种工况下的桥面板不同位置处横向应力分布图，如图6所示。

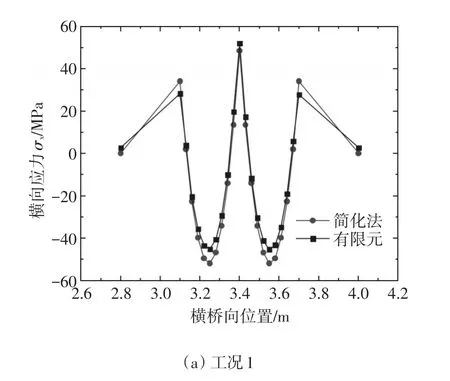
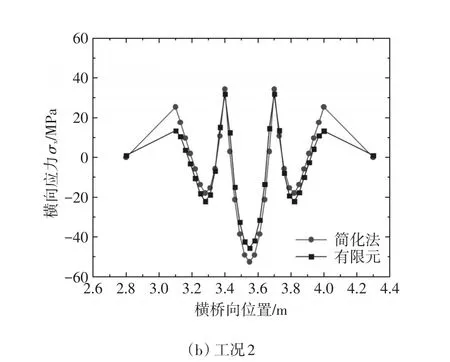
图6 两种方法桥面板不同位置处横向应力对比

由图6可知，在车轮荷载作用下，桥面板横向受力呈现出明显的局部性，在与一字肋交界处横向拉应力陡增，在直接承受荷载的两纵肋之间横向压应力陡增。两种工况作用下，桥面板最大横向压应力相差不大，但工况1作用下的桥面板最大横向拉应力略大。有限元结果与简化计算法所得结果吻合较好，表明按照此种解析方法能够快速准确实现轮载作用下带一字肋桥面板横向弯矩及应力的计算，提前预测开裂风险。但是使用简化计算的方法求得两肋之间桥面板的横向应力偏保守。类似地薛璞曾使用P-E法、梁格法与有限元所求解作比较，指出出现上述现象的原因一是桥面板与加劲肋腹板抗弯刚度存在较大差距；二是受到纵横肋支撑限制的桥面板还有较大的柔度，受力的局部性必然导致变形的不连续性，内力规律较复杂。简化计算法则忽略了一些因素，如文中在简化横隔板对桥面板约束为弹簧时，忽略了横隔板的抵抗扭转作用以及q的近似等效均布等。

3 组合桥面板计算及正确性验证

若在此正交异性钢桥面板上铺装UHTCC层，形成带一字肋钢-UHTCC组合桥面板。同时作如下计算假定：①钢桥面板与UHTCC层之间完全紧密连接，不产生相对滑动；②钢材和UHTCC为理想弹塑性体；③不考虑UHTCC层对于轮载的扩散效应。

则铺装后的单个含一字肋组合桥截面纵向抗弯惯性矩计算如下：

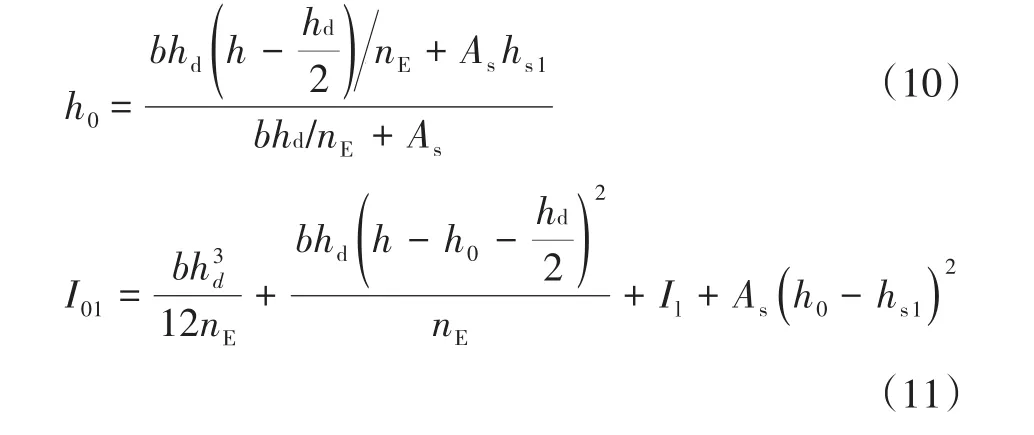
式中，nE为钢材和UHTCC弹性模量的比值；h0为换算截面形心至钢结构部分底面的距离；h为截面的高度；b为UHTCC层的宽度；hd为UHTCC层的厚度；As为钢结构部分的截面积；hsl为钢结构部分截面形心至底面的距离见图7。

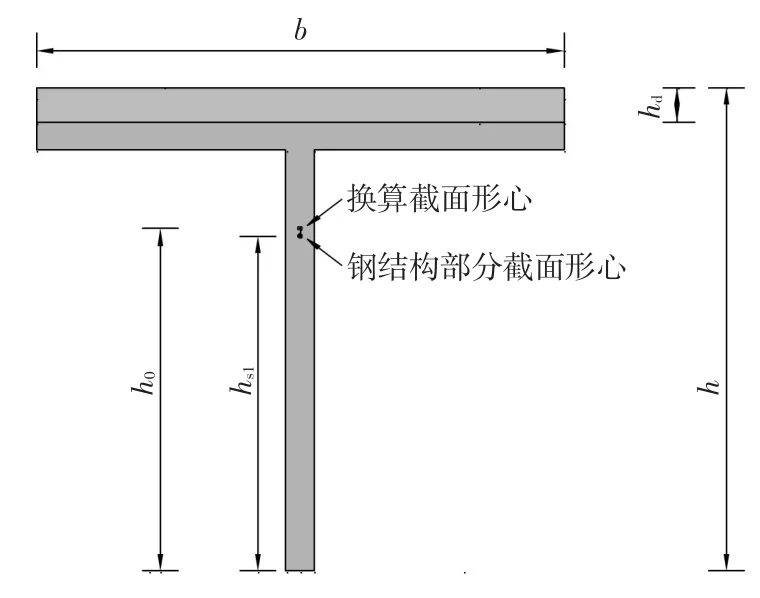
图7 含一字肋组合桥截面纵向抗弯惯性矩计算

由以上计算可知，铺装UHTCC层后桥面纵向抗弯刚度显著增大。同理，桥面板的横向抗弯惯性矩I亦增大为I02，且计算方式与式（10）和式（11）相同。将I01和I02代入至式（6）～式（8），便可求得钢-UHTCC组合桥桥面板不同位置处的横向弯矩M。桥面板下表面横向应力σx计算如下，此处M即为钢-UHTCC组合桥桥面板不同位置处的横向弯矩：

为了验证以上推导的正确性，在模型一的基础上铺装仅为20mm的UHTCC层，UHTCC弹性模量取19.3GPa［13］，分别利用简化计算法和有限元软件求得组合桥桥面板下表面横向应力计算结果。有限元模型二采用分层壳单元，可以较为全面地展示壳体结构的空间力学性能［14］，相比实体单元可大幅减少计算时间。分层壳单元的主要假设如下［15］：①混凝土层和钢筋层之间无相对滑动；②每个分层壳单元允许分层数不同，而且每个分层可以有不同的厚度，但是同一个分层厚度要保持均匀。

模型中UHTCC层和钢材层设置在同一个壳单元中。此外建立的有限元模型二与模型一其他设置完全一致。最终两种方法的计算结果如图8所示。

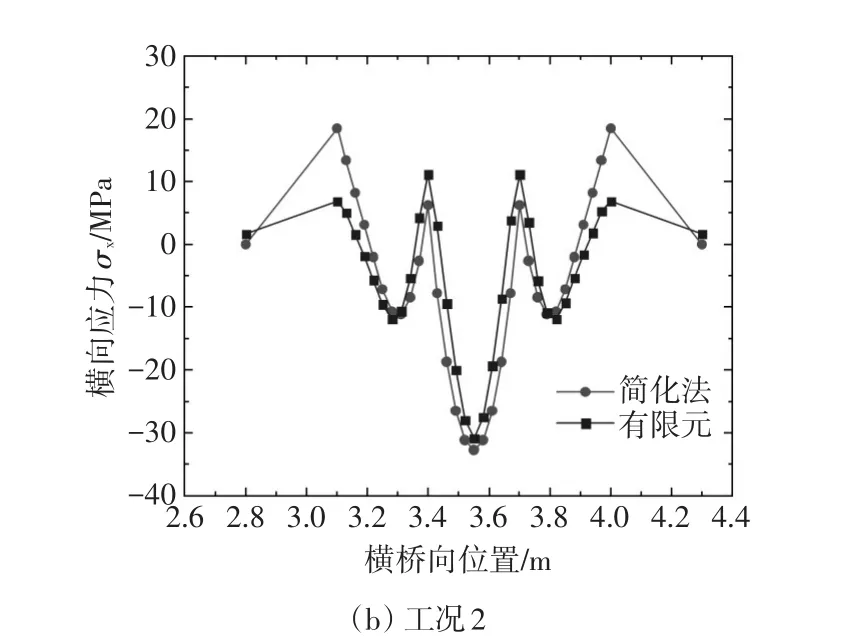
图8 两种方法带一字肋组合桥横向应力对比

由图8可知，两种方法关于钢-UHTCC组合桥的横向受力计算结果总体趋势相符，但在一字肋与顶板连接处出现较大误差，一部分原因在文中已阐述，另外，此处简化计算法未考虑UHTCC层的轮载扩散效应，若考虑荷载由于铺装后产生的扩散角度，两者之间的差异将降低。还有，将钢与UHTCC两种不同材料的截面换算成同一种材料钢截面，这种方法忽略了等效后截面的刚度变化，所得结果是近似解［16］，与实际情况也有微小差异。

4 铺装UHTCC层前后对比

综合文中的结果，将纯钢桥面板铺装UHTCC层前后采用简化计算法所得的横向应力结果对比如图9所示。

图9 铺装前后简化计算法横向应力结果对比

铺装20mm厚度的UHTCC层后，两种工况桥面板不同位置处的横向应力均有不同程度的降低，其中在与一字肋连接处拉应力降低幅度最大，此处工况1、2拉应力降幅最大均达到82%。经过以上分析可知，采用横向轮载效应简化计算法，在相同的荷载作用下，UHTCC层的铺设增大了原钢桥面的纵向一字肋底部弹性支撑刚度和顶板横向抗弯刚度，使得整个顶板结构能够承担更多比例的横向弯矩，有效降低了钢桥面板各个位置的横向应力，因而也降低了桥面板疲劳开裂风险。

5 结语

文中首先在考虑开口肋正交异性桥面板局部性受力特点的基础上，建立简化平面框架体系模型，经过理论推导给出了使用纵向加劲肋抗弯刚度求解钢桥面板和纵肋交界处的最大横向弯矩的解析表达式，利用有限元模型验证了算法的正确性；然后对开口肋组合桥横向受力性能进行理论分析，同样利用算例证明了简化计算法的可行性；文中研究的主要成果和结论如下：

（1） 文中所提出的横向受力简化计算法能够快速准确实现轮载作用下带一字肋桥面板横向弯矩及应力的计算，相比有限元结果，使用简化计算的方法所得横向应力略大，更偏保守。

（2） 组合桥面板相对于纯钢桥面板横向应力的降低，原因在于相同荷载作用下，UHTCC层的存在增大了原钢桥面的纵肋底部弹性支撑刚度和顶板横向抗弯刚度。

（3） 相同的荷载作用下，20mm厚度的UHTCC层有效降低了原纯钢桥面板各个位置的横向应力，其中在与一字肋连接处拉应力降低幅度最大，最大降幅达到82%。