基于“导弹制导打击”的虚拟仿真实验设计与探索

朱立华

（南京理工大学机械工程学院 江苏 南京 210094）

“数值计算方法”是一门研究用计算机处理各类数学问题的计算理论与计算方法的学科，是各学科领域研究过程中数据分析和处理的基础。因此，在大部分高等院校中该课程常被设置为理工科类本科生的必修课程。“数值计算方法”课程以“高等数学”“线性代数”和计算机编程类课程为基础，主要讲授误差分析、插值与拟合、数值积分与数值微分、常微分方程数值解法、代数方程数值解法、线性方程组数值解法等工程常用数值计算方法，利用计算机进行算法编程，旨在培养学生解决工程中实际问题的能力。在南京理工大学，该课程是机械工程、测控技术与仪器、航空宇航、电光科学、控制科学、车辆工程等专业本科生的专业必修课。

然而，该课程的教学过程中，学生普遍学习积极性不高，这其中既有主观原因，又有客观因素。从课程的特点出发进行分析，问题主要体现在以下两个方面。

第一，“数值计算方法”课程涉及大量“高等数学”和“线性代数”的基础理论知识，学生学习时需要回忆大量复杂的公式、定理及数学推导过程。学生的数学基础参差不齐，甚至部分学生潜意识中对数学的“恐惧心理”而学得不深入、理解不透彻，导致该课程的学习效果不理想。

第二，在算法理论学习的同时，用计算机软件进行算法编程实现是“数值计算方法”课程的一大特点，学生普遍缺乏对计算机逻辑的深入理解和计算机语言的熟练应用能力，导致算法的实践过程存在困难。

分析上述两个问题，主要是学生因数学理论的晦涩而学习兴趣降低，主观能动性弱。面对这一教学困难，高校教师开展了多轮教学改革以寻求解决方案，提高教学质量。自2013年以来，教育部先后开展国家级虚拟仿真实验教学中心、示范性虚拟仿真实验教学项目和虚拟仿真实验教学一流课程的建设。随着国家对虚拟仿真平台建设力度的不断增加，各高校在相关方面展开了积极探索，虚拟仿真实验教学已成为提升高等教育发展水平和全面提高人才培养质量不可或缺的手段。可见“虚拟仿真实验”教学设计不失为提高本课程教学效果的有效手段。

南京理工大学的兵器科学与技术学科是国家“双一流”建设学科，学校长期从事导弹武器系统的教学和科研，培养导弹武器系统方面的工程精英人才。依托学校特色，本科生培养内容包括枪、炮、弹、箭等各类型战术武器。其中，导弹作为兵器之王，国之重器，是打赢高技术条件下现代化战争的撒手锏，导弹武器系统方面的专业人才培养是国家国防建设的迫切需要。导弹的打击制导过程需要大量的算法支撑及数据分析需求，囊括了“数值计算方法”课程的全部知识点。因此，学校建立“导弹制导过程”的虚拟仿真平台，将“数值计算方法”课程的算法实践有序地贯穿于虚拟仿真实验中，不仅可以帮助学生深刻理解并掌握典型弹的运动特点，还可以增进学生对所学“数值计算方法”课程理论知识的理解，培养学生的工程实践能力和科研创新能力。

2 虚拟仿真实验原理和仿真系统设计

通常而言，导弹打击目标实验在真实条件下是很难实现的。一方面，该实验环境恶劣，场地条件要求苛刻，实验本身具有高度危险性，有可能造成人员安全事故。因此，学生很难有机会参与实验。另一方面，“数值计算方法”等数学应用类课程要求将数学理论知识应用于实践，原本是学生将所学理论与实践相结合的有效工具。然而，常因算法算例的问题背景与学生所学专业的相关性弱，导致学生学习效果不佳。针对这两个问题，教师对“数值计算方法”课程的课堂讲授及实验实践教学模式进行重构，本着“能实不虚，虚实结合”的原则，建设了模块化、层次化、可视化的虚拟仿真实验平台。这样不仅可以为学生提供安全环境下的导弹打击目标过程的深度体验，而且帮助学生了解导弹打击目标的总体设计过程以及各类数值算法的具体应用。本虚拟仿真实验设计思想如图1所示。

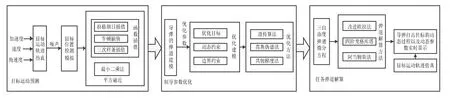
图1 实验原理框图

虚拟仿真实验应考虑一类发射制导的导弹，通过三维实景动画，实时显示动态参数曲线等虚拟仿真技术，让学生观察导弹打击目标的完整过程。本虚拟仿真实验主要分为目标运动预测与跟踪、制导参数优化和任务弹道解算三个模块，各模块层层递进，均包含各类数值分析算法的实景应用。

2.1 目标运动检测

在导弹打击目标之前，首先需要获取目标信息，并实时跟踪。目标信息主要包括目标的运动建模和观测数据拟合。在虚拟仿真实验中，雷达可扫描环境中的目标，以获取目标的实时位置。因此，构建雷达视窗，实时显示观测目标的位置，如图2所示（p47）。在连续获得位置数据的基础上，可以采用数值计算中典型的拉格朗日插值、牛顿插值方法和三次样条插值对目标的运动进行函数拟合，从而实现对目标运动的预测与跟踪。不仅如此，考虑到观测噪声的影响，可以选择数值计算中函数逼近类算法——最小二乘法对检测数据做最佳平方逼近，经回归分析得到目标的运动规律，从而实现对目标运动的预测。

图2 目标检测虚拟仿真场景

2.2 制导规划设计

在对目标实时检测的基础上，结合载体的运动状态，进行制导规划设计。导弹的总体规划是一个复杂的过程，具有很强的综合性。本虚拟仿真实验主要考虑以最快命中目标为制导准则的弹道参数计算，因此将该过程建模为一类约束规划问题。其目标函数为：

其中，、、为导弹的速度、俯仰角和偏航角。

设计的约束条件，包含动态约束和边界约束。边界约束包括对各参数的等式和不等式约束：

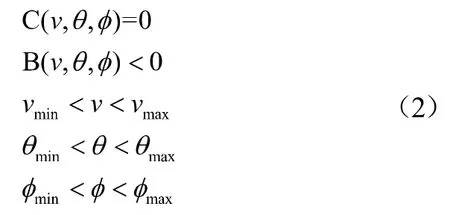
在显示了参数优化模型后，学生要选择适当的求解算法。参数优化算法的迭代求解可采用的方法分为直接优化算法、间接优化算法和全局最优算法三类。分别设置了高斯伪谱法、共轭梯度法和遗传算法作为这三类算法的典型算法作为求解手段备选，如图3所示。学生应了解三类算法的原理，并对比各算法的特点及适用性。

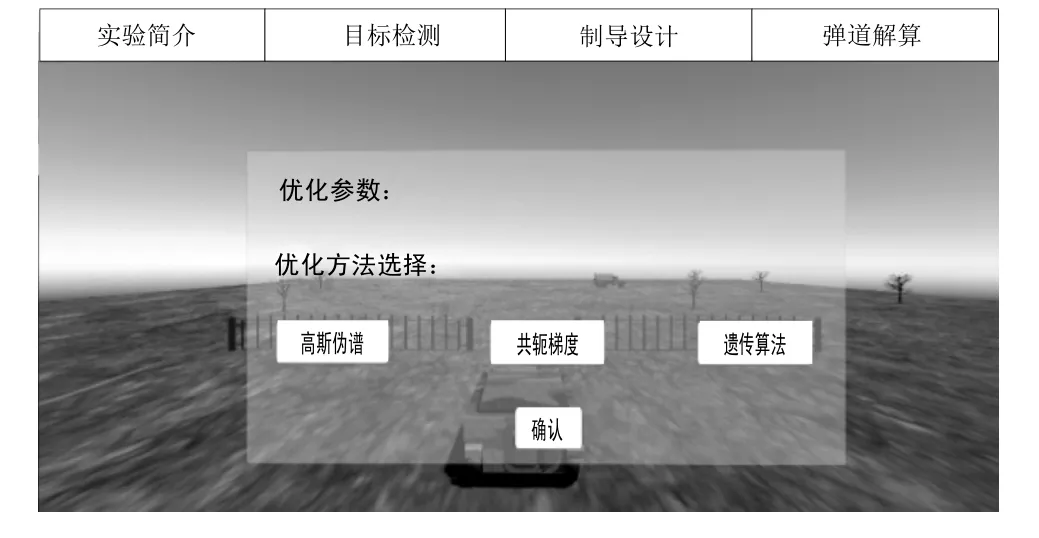
图3 制导设计方法选择

算法的求解过程体现了数值计算的迭代逼近特点，每次在设计参数的允许变化范围内产生一组设计参数。用这套参数连同输入的已知数据即可计算出目标函数值。目标函数值反映一个设计方案的优劣程度。若计算出的目标函数值较前一次计算值好，则保留，否则舍弃。再由优化法子程序产生一组新的设计参数。如此循环，直到按一定条件结束优化搜索，输出最后所选的结果。这一过程的流程显示和曲线显示并行展示在实验界面上，可使学生对整个流程的动态流向有更清晰的认识，帮助学生理解算法过程。最终，在选定方法并设置迭代停止条件后，得到制导参数初始值。

2.3 导弹任务弹道解算设计

本环节，根据得到的导弹初始条件，需要利用“数值计算方法”中的高阶常微分方程求解的手段完成对目标打击任务弹道的解算，并实施打击。本实验将欧拉法、四阶龙格库塔法、阿当姆斯法并列作为求解算法的选项，让学生通过选择不同的方法完成对导弹三自由度运动弹道的弹道解算。在实验界面的三维视图实时显示导弹打击目标的全过程（如图4所示），并分析导弹与目标的相对距离、导弹与目标的速度、位置、姿态等参数的动态性能。通过本环节，学生可以明确检验不同常微分算法的计算精度和求解性能。

图4 导弹制导过程示意图

根据以上各个模块的设计，学生可以反复做实验，在各个模块选择不同的方法，对比打击效果，加深理解。

3 实验方案和实验过程

按照任务牵引的“三阶段”混合式实验教学模式，实验过程包括知识学习、虚拟实验、考核评价和扩展提升四个环节。实验全部环节均需要学生进行人机交互式操作，亲身经历原理学习、实验观测、数据处理和结果分析整个过程，并以实验报告的形式提交实验成果。

3.1 知识学习

获取实验指导书，了解实验目的、实验内容和实验步骤。对实验设计的坐标系、运动参数分析、导弹的运动学方程、常微分方程的数值求解、轨迹规划、优化算法等知识进行查缺补漏，为实验做好知识储备。

3.2 虚拟实验

实验内容包括目标轨迹预测、制导优化设计、任务弹道计算三个实验模块，完成炮射导弹攻击坐标系认知、函数插值、约束优化设计、弹体运动学建模、常微分方程的数值求解等5个实验内容。各个实验模块既能独立运行，又能相互衔接，充分满足了学生不同学习阶段的能力培养需求。系统可在网页版或PC客户端运行，方便学生开展实验。

3.3 考核评价

教师应记录、分析和评价实验过程中学生的操作信息，学生完成三个实验模块的在线测试。之后学生上传实验报告，教师生成成绩反馈表。

3.4 拓展提升

学生完成交流讨论和巩固提升，教师线上批阅实验报告，在线指导学生。

4 结语

为培养新时代背景下的高素质国防专业人才，学校依托本校军工特色，设计了基于“导弹制导打击”的虚拟实验，将“数值计算方法”课程的知识点融入仿真实验中，通过对真实实验场景的重现，提高学生的学习兴趣，激发学生的学习主动性。学生可在实验指导书的引导下，自主操作设备，独立完成实验过程。虚拟仿真的每一个环节对应“数值计算方法”课程相应知识点。通过模拟操作导弹制导打击目标，学生可以加深对所学内容的理解，进一步积极思考，实时调整自己的学习目标。在此基础上，学校后续拟增加开放性课题研究，结合课堂授课环节的讨论分析，对研究型教学进行有益的探索和尝试。