再谈降维思考升维解题
——以2022年浙江省数学高考第19题为例
2022-08-16余建明曹凤山
余建明, 曹凤山
(1.淳安中学,浙江 淳安 321004;2.余杭区教育发展中心,浙江 杭州 321004)
文献[1]以2017年和2020年浙江卷第19题为例,回归原点,基于翻折策略主动降维把立体图形平面化.2022年是浙江省高考自主命题收官之年,数学试卷总体遵循“稳中求进”的原则,具有较高的区分度和难度,其中第19题重点考查线线垂直、线面垂直、面面垂直三者之间的转化,立意新颖.笔者以此题为例再谈降维思考升维解题,明修栈道暗度陈仓.
1 原题展示
例1如图1,已知四边形ABCD和CDEF都是直角梯形,DC∥AB∥EF,∠BAD=∠CDE=60°,EF=1,DC=3,AB=5,二面角F-CD-B的平面角为60°,M,N分别是AE,BC的中点.
1)证明:FN⊥AD;
2)求直线BM与平面ADE所成角的正弦值.
(2022年浙江省数学高考试题第19题)
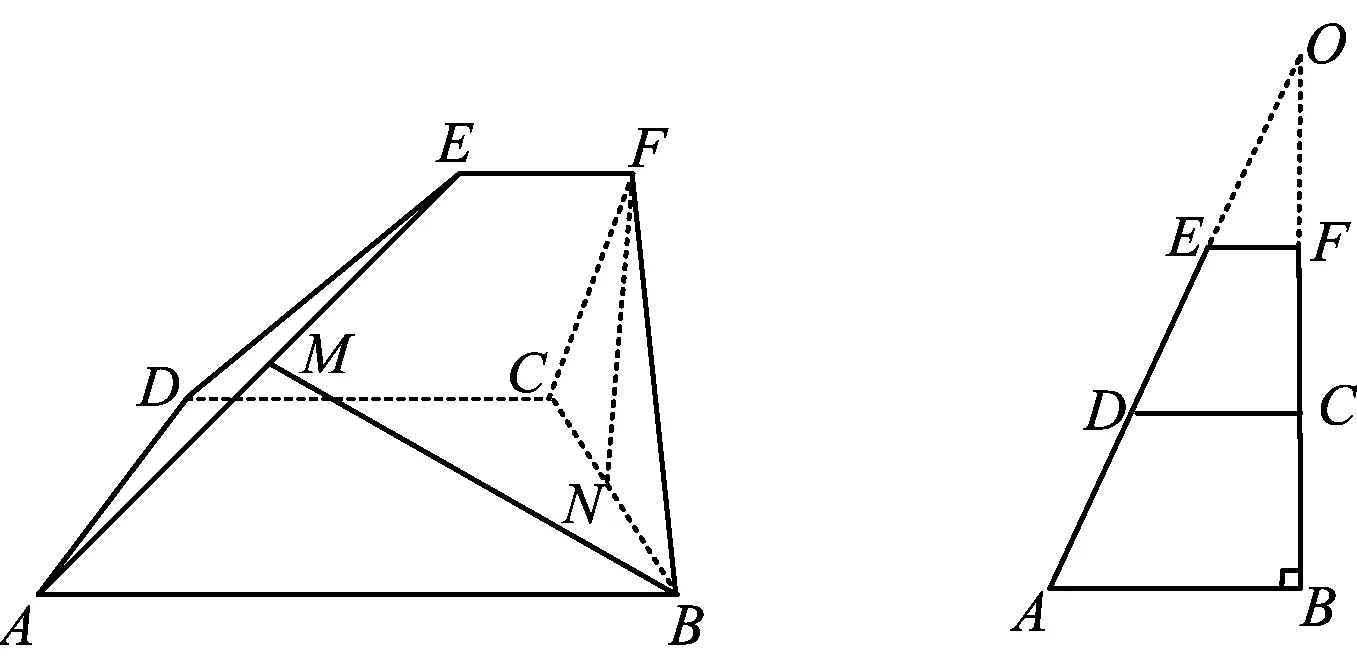
图1 图2
2 解法探究
1)证明把侧面直角梯形DCFE往下翻折,得到图2.因为∠A=∠CDE=60°,所以点A,D,E共线,又
∠B=∠DCF=∠EFC=90°,

图3
从而
DC∥AB∥EF.
由EF=1,DC=3,AB=5,得DC是梯形ABFE的中位线,故FC=BC.
因为∠FCB是二面角F-CD-B的平面角且∠FCB=60°,所以△FCB是等边三角形,从而
FN⊥BC.
又DC⊥平面FBC,从而DC⊥FN,于是FN⊥平面ABCD,故FN⊥AD.
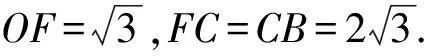
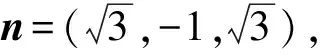
3 解后反思
3.1 栈道法则再回顾
如图4,在四边形ABCD中,过点D作AC的垂线分别与AC,AB交于点M,N.如图5,把四边形沿AC翻折成三棱锥D-ABC.
基本事实图6中AC⊥平面DMN,平面ABC⊥平面DMN,平面ACD⊥平面DMN.
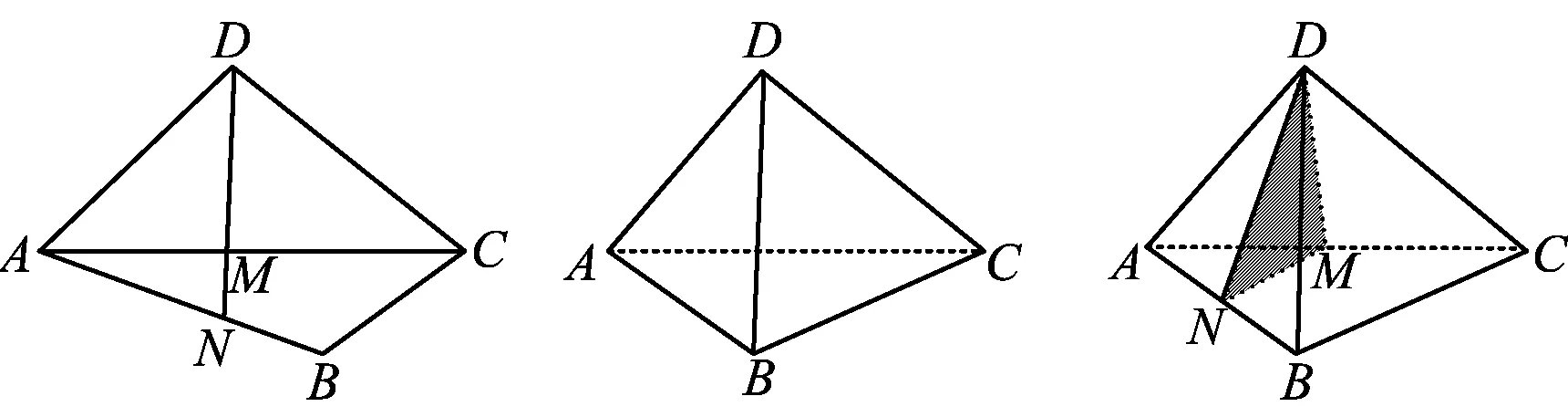
图4 图5 图6
栈道法则[1]我们把折线AC的垂线定义为栈道,图4和图6中的DM,MN就是栈道.栈道上的任意点在另一个平面(另一条栈道与折线所在的平面)的投影(定义为“仓”)必在另一条栈道上,即点D在平面ABC上的投影必在MN(栈道)上,点N在平面DAC上的投影必在DM(栈道)上.
3.2 为什么要翻
立体几何研究的是空间中的位置和数量关系,这需要学生有一定的空间想象能力和逻辑思维能力.虽然学生在初中阶段学习了立体几何初步,但高中阶段对直观想象和逻辑推理提出了更高的要求.几何图形首先让空间图形中的点、线、面从隐性到显性完整展示出来,回归原点,降维立体图形平面化“成就”了图形可视,栈道法则找垂足“成就”了度量可测.
本题的关键是确定点F在底面投影的位置,从形的结构看侧面FCB相对简单,但是构成三角形的元素不明确,侧面DCFE虽是直角梯形但是所有的元素都是确定的,把更多的线线垂直放在一起,自然而然想到把两个直角梯形降维翻折成同一个平面.由DC⊥FC,DC⊥BC,根据栈道法则的定义知,DC是折线,FC和BC是栈道,F在平面ABCD上的投影必在栈道BC上,又△FCB是等边三角形,可知投影就是BC的中点N.
3.3 还能怎么翻
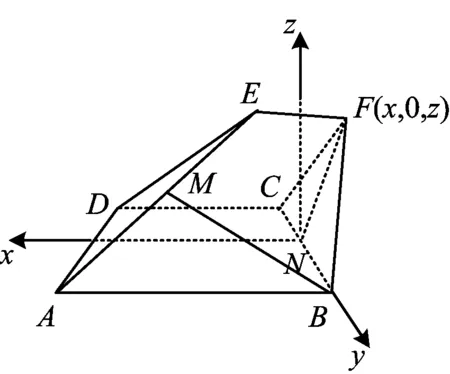
图7
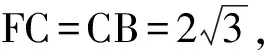
评注利用DC⊥BC,DC⊥CF,可得CD⊥平面BCF,由面面垂直性质定理(栈道法则)知无论平面DCFE怎么旋转,点F在底面的投影必在直线BC(栈道)上.
4 变式升华
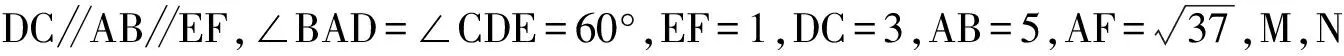
1)证明:FN⊥AD;
2)求二面角F-CD-B的平面角的大小.
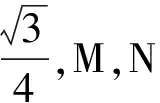
1)证明:FN⊥AD;
2)求二面角F-CD-B的平面角的大小.
变式3如图8,在多面体EF-ABCD中,底面ABCD是矩形,四边形DCEF是等腰梯形,EF∥CD,AB=2BC=2EF=2EC=8,△BCE是等边三角形.
1)求二面角E-CB-D的平面角的余弦值;
2)求多面体EF-ABCD的体积.
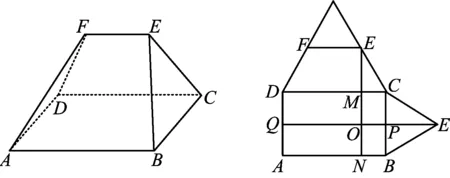
图8 图9
回归原点根据降维策略先把等边三角形EBC往右翻,如图9,由栈道法则知点E在底面的投影在BC的中垂线PQ上,再把等腰梯形DCEF往后翻,知点E在底面的投影在MN上,结合两条栈道直线PQ与MN的交点O就是点E在底面的投影.
解1)如图10,分别取AD,BC的中点Q,P,在边CD,AB上取点M,N,使得CM=BN=2,PQ与MN交于点O.因为BC⊥PQ,BC⊥EP,所以
BC⊥平面EFQP,
从而
BC⊥EO.
又DC⊥EM,DC⊥MN,从而
DC⊥平面EMN,
于是
DC⊥EO,
故
EO⊥平面ABCD.
又∠EPO是二面角E-CB-D的平面角,从而
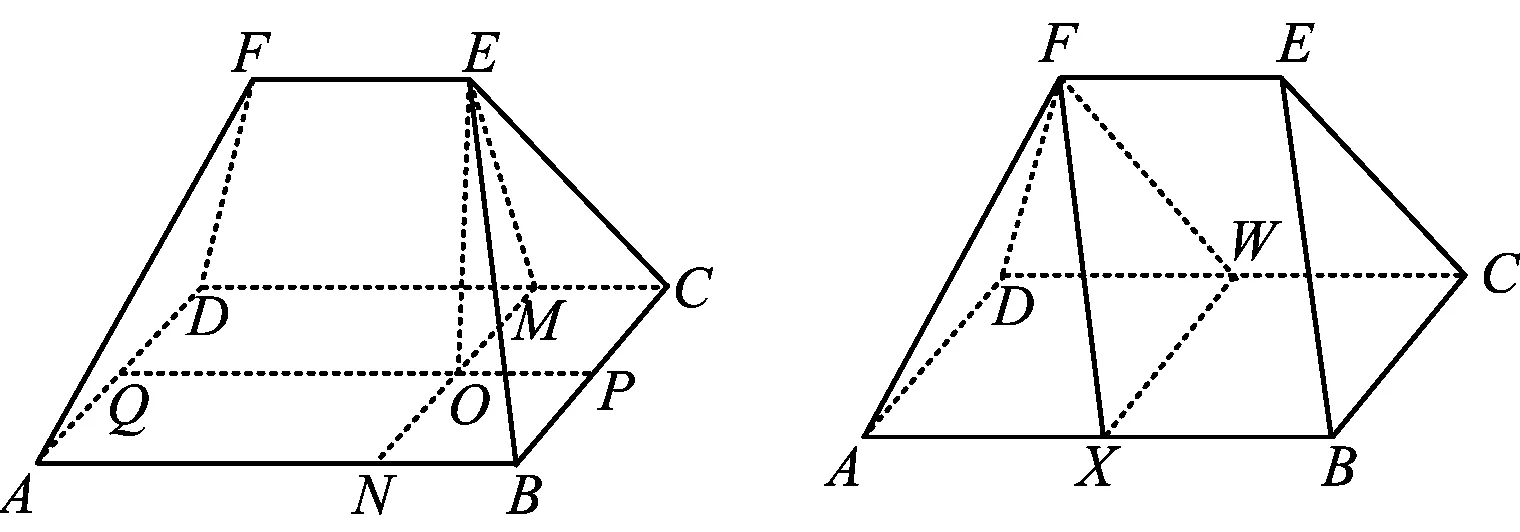
图10 图11
2)取AB,CD的中点X,W,联结FW,FX,WX,则多面体EF-ABCD被分割成一个锥体和一个柱体(如图11).设多面体EF-ABCD的高为h,则
VEF-ABCD=VF-AXWD+VFXW-EBC
设计意图根据面面垂直的性质定理只能确定点在面的投影在两个平面的交线上,要确定点的位置还需一个面面垂直.若用降维思考升维解题策略,则只需翻折两个侧面,修两次栈道找交点即可.
年年岁岁花相似,岁岁年年人不同,铁打的营盘流水的兵,2017年和2022年浙江卷第19题以及2021年和2022年多地的模拟题情境都在变,面面垂直从台前走向幕后,但不变的是主动翻折“降维”思考,不变的是修“栈道”找“垂足”,不变的是在“想”的基础上有效“算”.
