太阳能并网发电系统的无功电压最优控制

国网青海省电力公司经济技术研究院 安 娟 张祥成 黄存强 程文俊

中国电建集团西北勘测设计研究院有限公司 张 娉

传统能源占比减少将导致电网调压能力减弱，为此各国出台一系列光伏发电并网标准，要求光伏发电提供无功备用以保障电网的稳定运行。太阳能电池板通常通过并网变换器将能量馈入电网，因而具备灵活调节有功和无功的能力，有能力快速响应电力系统的电压突变。塔式光热发电系统具有能量集中、过程简单的特点，适用于商业化应用。将塔式光热发电系统与光伏发电系统相结合抑制电压波动，具有协同增效的优势，但需可行的控制策略。

有鉴于此，在光伏渗透率较高的场景下，对光伏系统、塔式光热系统的无功输出进行最优调度，可提高电网的电压调节能力。然而太阳能电站的最优无功调度依赖于行之有效的控制策略，决策各个光伏阵列、光热系统的最优无功功率。此外要保障各个可调度太阳能发电系统的稳定需受制于一系列约束，因而这是一个含约束的在线最优控制问题，粒子群算法是求解该控制问题的有效方法。同时，为实时保障太阳能发电系统的最优无功出力，一方面对于每个光伏阵列需满足对最大功率点的跟踪，实现总功率的最优；另一方面，并网变换器的控制策略需具备最优性。

本文以光伏发电、光热发电作为被控对象为例，考虑使用双层控制架构：基于时变压缩粒子群算法，控制策略的上层考虑底层光伏阵列需满足的约束，决策出下层各光伏阵列和塔式光热发电的无功参考；下层光伏控制器前级负责追踪光伏阵列最大功率点、后级负责实时跟踪指令，决策出本地控制单元的开关指令，以控制无功功率的输出，最终在电网电压发生突变时及时参与电压控制，提高电网调压的能力和电压稳定性水平。

1 控制策略设计

1.1 系统模型

太阳能电站包括n个光伏阵列、1个塔式太阳能光热发电系统、升压变和并网逆变器。为建立有效的控制策略，首先需获取系统的控制模型。电压控制与无功功率相关，根据泰勒近似，在系统某一节点Y工作点电压VY与注入的有功、无功表达式为：

式中：VY[0]表示初始电压，ΔPS,i和ΔQS,i表示光热发电、各个光伏阵列有功/无功注入的变化。∂VY/∂PS,i和∂VY/∂QS,i是电压对功率的偏导，由此建立了线性的电压预测模型。电压对功率的偏导可通过求解潮流方程，根据得到的雅可比矩阵获得。由于有功对电压的影响非常小可忽略，因此上述模型可简化为：

1.2 控制策略设计原则

本文的太阳能并网发电系统参与电网无功电压控制，控制系统的总体目标为：求解最优控制问题，得到最小的控制输入，该输入在满足约束的条件下，保证参考轨迹和预测轨迹尽可能重合，本光伏系统共有3个光伏阵列(图1)。本控制策略分为两层：考虑各太阳能发电系统约束条件，决策出各发电系统的无功最优出力；调度各个对应发电系统，实时跟踪该最优出力。为保证最优地实现所有的控制目标，上层使用时变压缩粒子群算法(PSO)求解最优控制问题，决策出最优无功出力来抑制电网电压波动。下层使用PID、有限控制集的模型预测控制(FCSMPC)等控制方法，保证上层的无功出力能得到最优的执行。

图1 控制系统结构图

1.3 上层控制策略设计

上层控制器的首要目标为，使得并网节点Y处电压波动尽可能小，即在每一时刻T电压波动值ΔV尽可能接近于0；次要控制目标为，为保证太阳能电站的效益，无功出力应尽可能小、有功出力尽可能大。基于此，T时刻建立优化目标函数：

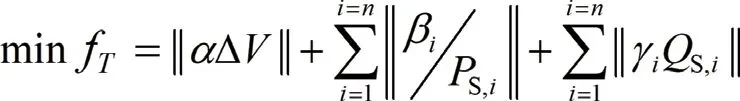
式中：α、β、γ均为权重因子，可视为对各项的惩罚，该惩罚量大小与光伏阵列、塔式光热系统容量相关。为保证所得结果满足控制目标，需按照目标优先级设置权重因子大小，越重要的目标惩罚越大。令β足够小，忽略有功的影响。同时各个光伏阵列的功率出力需满足容量约束，即有功无功出力需在设定的范围内，以保证光伏阵列合理运行。约束条件如下：该问题为非线性的约束优化问题，需高效可行的求解策略，时变压缩粒子群算法是解决这一问题的可行途径[1]。

1.4 上层控制求解策略

优化问题可使用粒子群算法来求解，该算法不是唯一的求解方法但具有快速性。为建立初始粒子群种群，对各发电系统无功调节量进行随机编码，表示为：

式中：m表示粒子种群规模；N表示每个粒子所载信息维度，具体到本次模型N也表示可调度发电单元总数。上述的每一个粒子即为一个满足各项约束条件的初始可行解。通过迭代计算，即可计算出各个可行解情况下目标函数，确定各发电系统最优无功调节量。

压缩粒子群算法为Clerc等提出的一种改进粒子群算法，具有求解快速的优点，其粒子位置和速度迭代方程为：xi(t+1)=X(t)+vi(t+1)、vi(t+1)=ρvI(t)+C1rand()(Pi-xi(t))+C2rand()(Gixi(t))。

式中：xi(t)、vi(t)为第i个粒子在第t次迭代过程中的位置和速度；C1、C2为加速因子，rand()为随机量；Pi为个体极值，Gi为全局极值；ρ为压缩因子，其表达式如下：φ=C1+C2。

为使上层控制策略性能更加优良，本文采用了时变压缩粒子群算法，其采用双重压缩因子ρ1和ρ2。双重压缩因子基于压缩粒子群算法提出，其表达式如下：xi(t+1)=X(t)+vi(t+2)、vi(t+1)=ρ1vi(t)+C1rand()(Pi-xi(t))+C2rand()(Gixi(t))、vi(t+2)=ρ2vi(t+1)。

通过迭代，最终确定各个光伏阵列、塔式光热系统无功输出给定。迭代终止的条件有两种，分别为收敛条件和最大迭代次数。当迭代中满足两者之一时均可终止迭代。

1.5 下层本地控制策略设计

下层控制包括光伏发电、光热发电的控制。对于光热发电，其工作机理是通过熔盐储热，最终通过汽轮机驱动同步电机发电，同步电机采用传统控制即可满足较稳定的控制效果。对于下层光伏阵列，为保证对无功的控制，需要将有功、无功控制进行解耦。同时下层控制需能满足最大功率点追踪的需求，以实现有功功率的最优。因此前级使用PID控制实现对光伏板最大功率的追踪、后级使用FCSMPC，以实现对并网功率的控制，即实现有功和无功的解耦控制。

1.5.1 前级buck控制策略

前级buck的主要控制目标为实现对光伏板最大功率的追踪。考虑如图2所示buck模型，分析过程中先认为后级逆变为恒电阻负载。其中，Vi为光伏板输出电压，即buck输入电压；Ci、Co分别为buck输入、输出电容；L为主功率电感；IL为电感电流；Vo为输出电压。不考虑控制延时可得开环传递函数为G(s)H(s)=G(s)/(S2LCo+sL/R+1)。

图2 前级buck模型

被控对象为二阶系统，需保证有充足的开环增益，足够大的穿越频率，且在谐振峰处系统稳定。由于被控对象具有两个极点，作为补偿、控制器应有两个零点；同时，为提高低频增益且减小稳态偏差，控制器需有一个极点。因此需使用PID控制器，前级buck控制光伏板输入电压，使其寻找到最大稳态功率工作点，使得光伏板的输入功率达到最优。

1.5.2 后级逆变控制策略

后级控制主要实现有功、无功并网控制，为使有功、无功功率控制解耦，简化控制过程，且保证控制策略的最优，后级控制使用FCS-MPC，该策略在有限控制集中选取最适合当前控制目标的控制输入，因而是最优的。为实现对并网变换器的最优控制，考虑如图3并网系统的控制模型。其中：I代表开关元件，Vg代表电网电压，Vbus代表母线电压。首先需建立被控对象的预测模型，根据KVL三相逆变器的模型如下[2]：

图3 后级逆变模型

其次，对于FCS-MPC，需基于模型确定控制集，即控制输入的可行解集合。该系统控制状态定义如下：

其中，D代表开关状态。相应地，根据8种不同的开关状态g1、g2、…、g8，定义电压矢量控制集{V1,V2,…,V8}如下，共8种不同的控制矢量。

定义电压和电流矢量如下，将三相交流电压和电流写成矢量形式，最终可得控制模型如下：e=2/3(ea+δeb+δ2ec)、i=2/3(Ia+δIb+δ2Ic)、V=LdI/dt+e，其中，δ=ej2π/3。本文采用前向欧拉法，将控制模型、代价函数转化为如下形式：i(k+1)=i(k)+Ts/L(v(k)-e(k))、g=|i＊α(k+1)-iα(k+1)|+|i＊β(k+1)-iβ(k+1)|。

图4 典型电压矢量控制集

最后在每一时刻k，从控制集中选取开关变量作用于式，计算出使得g最小的开关变量作用于系统，此时即可保证预测曲线与目标曲线尽可能接近，达到跟踪参考输入目的。

2 仿真研究

2.1 仿真模型

为验证本策略有效性进行仿真研究，使用典型的两区四机系统（图5），仿真系统主要包括3个常规发电机、太阳能电站、变压器、输电线路等。光伏阵列、塔式光热系统分布在同一太阳能电站的不同地点，在节点10通过升压变连接到电力系统。图中的常规同步机容量分别为563MVA、155MVA和432MVA。原始负荷水平为875MW、312MVar。光伏系统额定容量为120MW，光热系统额定容量200MW，光伏发电的无功备用容量设置为30%额定容量。为实现电压突变，在t=2s时改变负荷水平，负荷消耗的无功功率增加200MVar。

图5 电网仿真结构图

2.2 仿真结果

图6显示在功率给定发生变化时下层控制器的控制效果。作为执行机构，下层控制器的主要功能在于按照参考指令快速地控制输出的无功功率。在功率给定发生突变时，实际功率输出能实现快速跟踪，动态性能好且无超调。当电网无功波动时能快速地抑制波动幅度，同时不调节过度。图7给出本控制策略下电力系统电压的变化。太阳能发电能够提高峰值电压，改善了暂态电压，电压峰值从0.9147p.u.增加到0.9229p.u.；母线电压稳定于0.9762p.u.，太阳能不参与调压时母线电压稳定于0.9542p.u.。根据上述分析，本策略有效减小了电压突变的影响，维护了系统电压的稳定。

图8给出了上层控制所决策出的光伏、光热系统无功功率变化。负荷突变导致电压波动，光伏系统提供了大量的无功功率，支撑电网电压，极大地减小了电压波动。从图6、图8可看出，各光伏发电系统的无功出力均快速、无超调，不会导致电压发生二次波动。可见本双层最优控制策略能满足功率约束，出力稳定，保障太阳能电站本身的安全稳定。

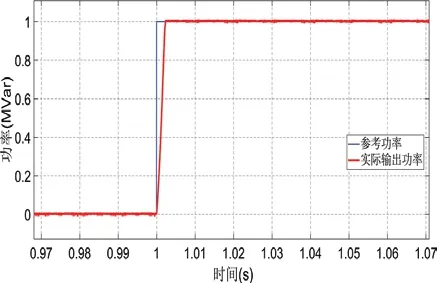
图6 下层FCS-MPC控制

图7 负荷突变后电压特性

图8 各可调度单元的无功出力