大型船舶低速柴油机柔性曲轴的三维振动研究
2022-08-16丘启发
丘启发
(中远海运船员管理有限公司 上海分公司,上海 200090)
0 前言
与陆用中小型柴油机相比,大型船舶低速柴油机的曲轴扭振、纵振和横振更为剧烈,且其作业功率密度和爆发压力均偏高,行程超出了普通柴油机的作业标准,容易发生船体与机体耦合振动,甚至造成轴系断裂事故[1]。为了降低事故的发生概率,需进一步探究此类型柴油机柔性曲轴的三维振动特征,从而为优化船舶制造产业提供参考[2]。由于振动特征的获取是建立在柔性机体与柔性曲轴耦合的基础上,因此有必要构建相应的耦合振动模型并展开深入研究[3]。目前,关于这方面的研究较少,尚未形成完整的耦合振动模型。本文利用柔性机体与柔性曲轴的动力方程构建耦合振动模型,并计算柔性曲轴,从而获得柔性曲轴的三维振动特征[4-5]。
1 耦合振动模型
由于柔性机体有限元模型的自由度数量超出了普通标准,因此曲轴与机体之间的油膜润滑容易对轴承负荷造成影响,使其呈现非线性特征,在仿真计算求解方程时需要耗费大量时间。本文引入Craig-Bampton模态综合法,减少了柔性机体的自由度。考虑到曲轴刚体的转动惯性,构建了柔性曲轴运动方程,将该运动方程进行转换处理,构建耦合振动模型。对曲轴和机体进行耦合处理时,同样可以通过转换方程,将其代入原方程中,最终可得到缩减后的耦合运动方程。
2 柔性曲轴计算
选取某大型船舶用低速二行程柴油机(MAN 6S50MC-C)作为研究对象,根据连杆活塞组件的惯性力和气体压力计算得出柴油机负荷。在发动机运转过程中,负荷周期性施加在各个曲柄销上,同时发动机机体各个部位受到气体压力和侧推力影响,导致发动机作业状况发生变化。另外,曲轴在柴油机飞轮端施加有一定扭矩,此部分扭矩在计算过程中也应考虑。该型号柴油机的主要技术参数见表1。
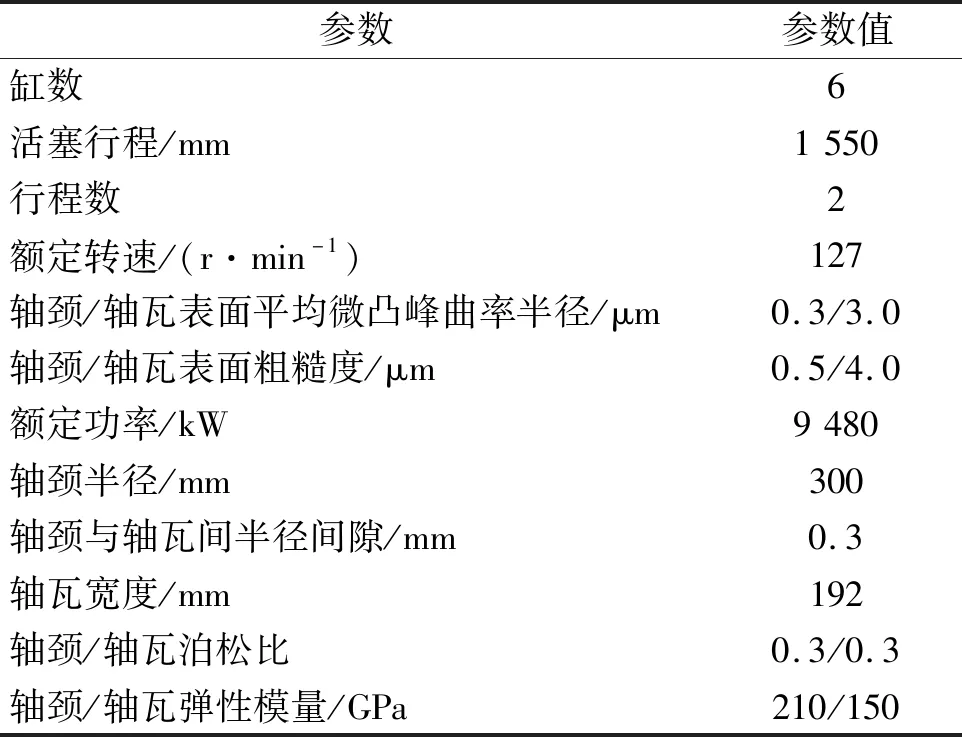
表1 柴油机主要技术参数
本文在研究柴油机柔性曲轴问题时,引入了改进后的Reynolds方程,并利用有限体积法计算。此外,轴瓦和轴颈的变形量也需要考虑在内。通过构建油膜厚度求解方程作为轴承润滑的分析工具。当轴瓦与轴颈之间的润滑方式为混合润滑时,会产生一定压力,即微凸峰接触压力,因此以Greenwood-Tripp微凸峰接触理论为基础,按照各参数的关系特点计算各个润滑区域内的压力[6]。关于主轴承负荷的求解,可采用数值积分法计算得到,包括微凸峰负荷和油膜负荷。
3 计算结果与分析
为了验证所提出的曲轴三维振动模型的可靠性,以扭转振动和轴向振动作为测试项目,选取热弹性流体运动学方法和非线性弹簧方法作为对照,对比分析拟合结果。
扭转振动和轴向振动的拟合振动曲线如图1和图2所示。由图1可知,本文模型的振动拟合结果与热弹性流体运动学方法拟合结果接近,与非线性弹簧方法的拟合结果稍有偏差。由图2可知,3种方法的拟合结果基本一致,当曲轴转角超过270°后,局部出现微小偏差。需要说明的是,本文模型对水平振动和垂直振动的拟合结果与非线性弹簧方法拟合结果具有一定偏差,但曲线的总体变化趋势相同。
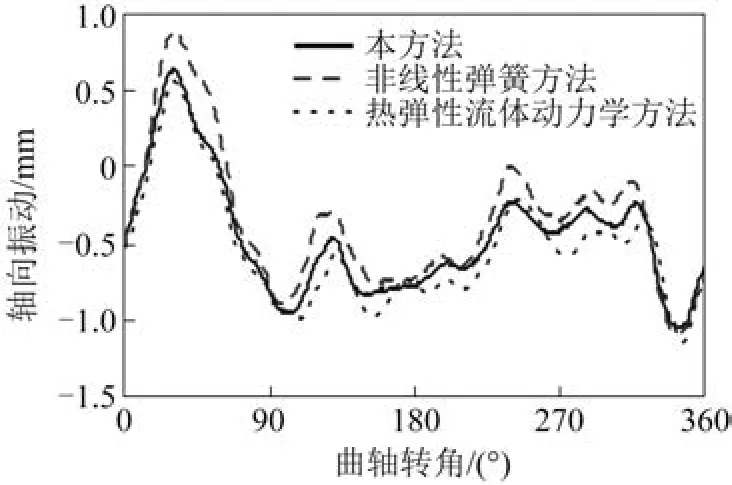
图1 轴向振动拟合结果对比

图2 扭转振动拟合结果对比
总体来看,本文模型的扭转振动和轴向振动拟合结果与其他2种方法的拟合结果吻合较好;从时间层面来看,本文模型计算耗时适中。因此,本文模型的构建方法可以在轴系三维振动计算中应用,且在经济性和准确性方面具备一定优势。
采用本文模型对整个周期内曲轴轴颈中心点的内扭转振动进行模拟,可以得到角位移随曲轴转角变化的拟合结果,如图3所示。结果显示,5号主轴颈中心与自由端的扭振振幅呈上升趋势,位于自由端的扭转角最大值达到了0.4°,基本与极限值相同。飞轮端与活塞推力侧之间的振幅也呈上升趋势,但与之对应的扭振角数值为负,其中最大值为-0.3°。在单个周期内,扭转振动曲线出现了6个峰值,由此可知,柴油机各缸周期性点火对曲轴扭转振动造成影响。需要说明的是,自由端至6号主轴颈中心之间的扭振振幅变化并不显著;随着与飞轮端距离的增加,飞轮端对曲轴扭转振动的影响逐渐减小;各缸点火时间与扭振峰值未实时对应,存在20°的曲轴转角迟滞,出现该现象的主要原因是曲柄销切向力会对扭振峰值造成影响[7]。
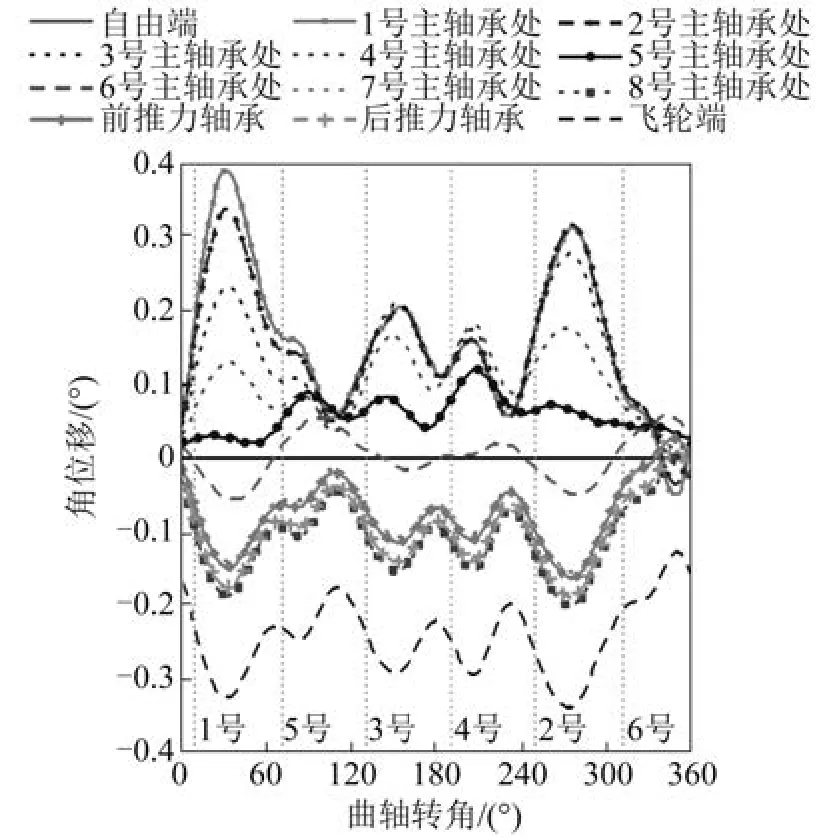
图3 曲轴轴颈中心点整周期内扭转振动
4 结语
以大型船舶低速柴油机为例,利用柔性机体与柔性曲轴的动力方程构建了耦合振动模型并开发了模型作业流程,同时为了验证本文方法的可靠性,将其与热弹性流体运动学方法和非线性弹簧方法的拟合结果进行对比分析。结果显示,本振动模型在经济性和准确性方面具备一定优势,可为分析曲轴扭转振动问题提供参考。
