基于带时间幂次项的灰色马尔可夫模型的中国能源强度预测研究

邹 圆 王立威

（1 重庆工商大学经济学院，重庆 400067；2 六盘水师范学院物理与电气工程学院，贵州六盘水 553004）

能源强度是国内生产总值（GDP）所消耗的能量，反映了一国或地区能源利用效率、经济结构、经济发展方式的变化，对其准确预测有助于科学把握经济发展的现实特征。其与现实中广泛存在的一些预测问题相似，均带有非线性、时变性和不确定性的特点，加之样本数据量少、波动大、影响因素众多，因而对其精确预测是一个既复杂又极具挑战的重要课题。目前所采用的方法大致可归纳为四种类型：传统统计学模型、神经网络模型、灰色预测模型和组合预测模型。传统统计学模型包括博克思（Box）和詹金斯（Jenkins）提出的时间序列自回归积分滑动平均模型（Autoregressive In⁃tegrated Moving Average Model，ARIMA）［1］、多元线性回归［2］、二次指数平滑法［3］等。其缺陷在于难以刻画预测问题中的非线性情形，易造成预测误差偏大且整体趋势拟合度偏低。BP 神经网络作为一种非线性建模方法，其多层前馈神经网络能以任意给定精度逼近任意非线性函数，常被用于各种预测如税收预测［4］、GDP 预测［5］等，但对训练样本数量与质量要求较高，适应范围和预测精度往往受到制约［6］。

灰色系统理论是由邓聚龙教授于1982 年首次提出的一种能有效针对小样本、贫信息系统的不确定性理论［7］，随后被广泛应用于经济、管理、电力、机械、生物医学等领域［8-12］。GM(1,1)是灰色系统中的经典模型，它的核心思想是以一条较为平滑的指数型曲线去拟合原始数据序列。而其固有缺陷在于对随时间阶段发展特征不一，即带时间幂函数项的非齐次指数数据序列拟合较差、预测精度较低。钱吴永等［13］将传统灰色GM(1,1)模型推广到含时间幂次项的灰色GM(1,1,tα)模型，并通过具体应用检验了所构建模型的有效性。崔杰等［14］揭示了该模型的病态特征，表明其鲁棒性较强。吴紫恒等［15］提出一种改进的含时间幂次项灰色模型，进一步提高了模型的拟合与预测精度。马尔可夫链作为一个离散变量的随机过程，通过状态转移概率矩阵将前后状态联系起来，该过程要求具备特定类型“无记忆性”，即下一状态的概率分布只能由当前状态决定，能提升灰色模型的适用性和预测精度。灰色马尔可夫模型在能源消费［16］、事故预测［17］、医疗需求［18］、设备故障［19］、财务危机预警［20］等领域得到具体应用。灰色马尔可夫模型与传统GM(1,1)模型共同缺陷在于不能很好处理现实中广泛存在的带非齐次指数规律的预测问题。

基于此，本文构建了带时间幂次项的灰色马尔可夫预测模型。其集成了带时间幂次项的灰色模型和马尔可夫链的各自优点，适用范围和预测精度都获得较大提升。主要体现在三个方面：一是不受样本量限制，能有效克服训练样本数不足的问题；二是根据具体问题确定时间幂次项指数，可以有效拟合带齐次指数或非齐次指数规律的数据序列；三是马尔可夫链针对偏差较大的预测结果序列提取状态信息转移规律，进一步增强预测精度。本文将之应用于中国能源强度预测问题并进行了模型预测精度的比较分析，证实了所提模型的有效性和可行性。

1 带时间幂次项的灰色马尔可夫预测模型构建

本节首先简要回顾了灰色GM(1,1)和带时间幂次项的灰色GM(1,1,tα)模型，通过引入马尔可夫链，构建了带时间幂次项的灰色马尔可夫预测模型并给出了相应的算法流程，为了比较不同模型的预测能力，介绍了一些常用的定量评价指标，为接下来对中国能源强度的预测奠定了方法基础。

1.1 带时间幂次项的GM(1,1,tα)模型

1.1.1 灰色GM(1,1)模型

在对现实问题预测中，影响考察对象的因素众多，且易受到各种随机冲击，从而表现出不同程度的不确定性和非典型波动特征。灰色模型具有不依赖样本分布、所需数据量较少、计算简便、预测精度较高等优点，可根据待考察对象变动的时间序列特性，挖掘其内部变化规律，预测结果较为准确且稳定。传统灰色GM(1,1)建模基本流程如下：

Step 4:由于上述累加生成序列X(1)与一阶线性微分方程的解曲线相似，因此可以导出GM(1,1)模型中的白化微分方程如下：

Step 5:用最小二乘法解得白化微分方程中的参数a,b为：

其中，a称为发展系数，b称为灰色作用量。

Step 6:将参数向量代入微分方程并进行求解，得：

Step 7:将上式进行累减还原，获得预测值：

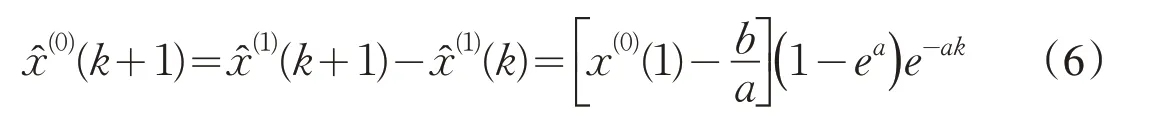
1.1.2 灰色GM(1,1,tα)模型

传统GM(1,1)模型对满足齐次指数规律的数据序列具有较好的预测效果，但现实中存在许多系统，其发展和演化规律无法简单采用指数规律来精确描述。通过考虑时间幂次项对传统灰色模型进行修订，以期准确反映在现实预测问题中大量存在的非指数规律变化特征，灰色GM(1,1,tα)建模过程如下［13］：

令α为非负常数，Step 1和Step 2同上，构建新的矩阵B和常数向量Y如下：

当α=0 时，GM(1,1,tα)模型退化为传统GM(1,1)模型，预测值如公式（6）所示；当α=1 时，GM(1,1,tα)变为GM(1,1,t)，预测值为：

当α=2 时，GM(1,1,tα)变为GM(1,1,t2)，预测值为：

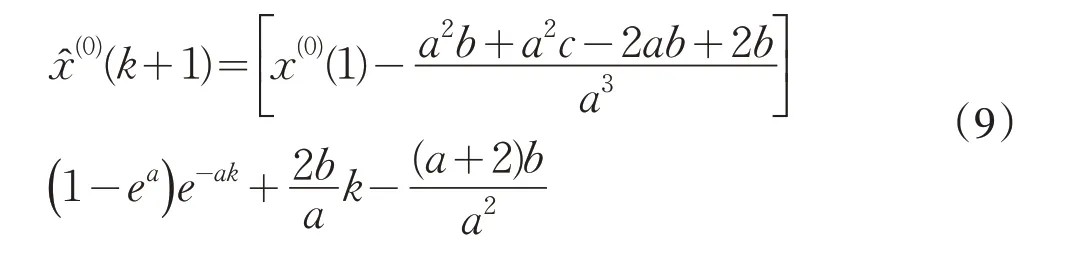
1.2 马尔可夫链修正

在进行预测中往往受到一些未知或随机因素的影响，如随机的外部冲击，导致数据出现一定的波动性和无序性，这对灰色模型的预测精度影响较大。可用马尔可夫模型抽取数据序列波动信息，修正灰色模型预测结果，来提高预测的精确度。首先利用灰色模型获得预测值，求出比率序列{s(k)}，；其次对比率序列进行状态划分，确定比率序列中各值所处的状态，获得状态转移概率矩阵；最后根据初始状态的概率向量和状态转移概率矩阵来推测预测对象未来某一时间所处的状态和预测值。其建模包括三个基本步骤：第一，划分状态序列；第二，建立状态转移概率矩阵；第三，确立新的经修正后的预测值。

将比率序列{s(i)} 划分为m个状态，记作{Q1,Q2,…,Qm}，每个比率值s(i)可唯一地划入状态Qj中，即满足s(i)∈Qj。其中Q j满足：

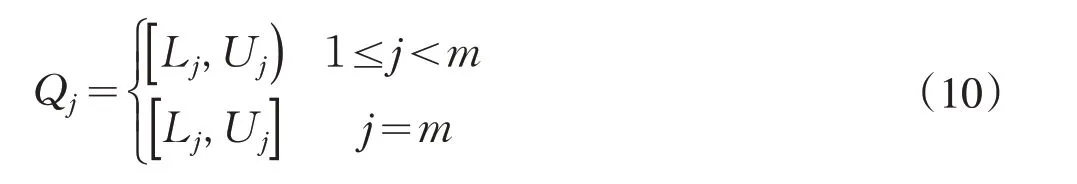
这里Lj、Uj分别表示状态Qj的下限和上限，满足：

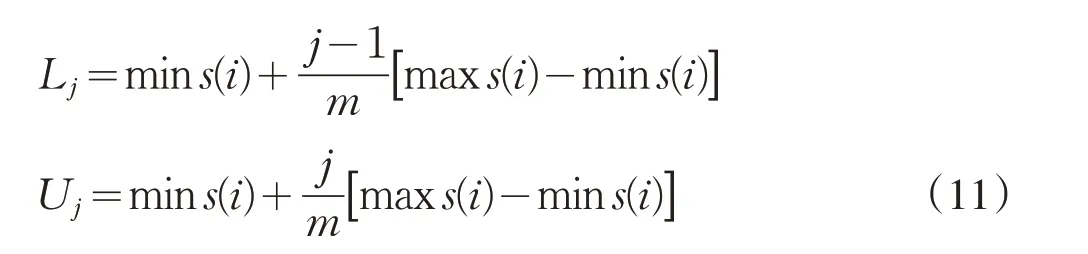
用Pij(λ)表示预测对象由状态Qi经过λ步转移至状态Qj的概率，该λ步转移概率可近似由转移频率来估计，即：

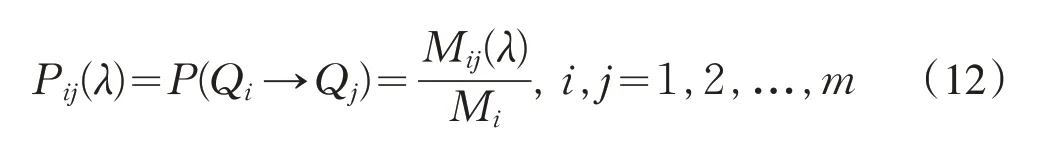
这里Mij(λ)为状态Qi经过λ步转移至状态Qj的比率序列样本数，Mi为处于状态Qi的比率序列样本数。由Pij(λ)组成的矩阵即是马尔可夫链中的状态转移概率矩阵，即：

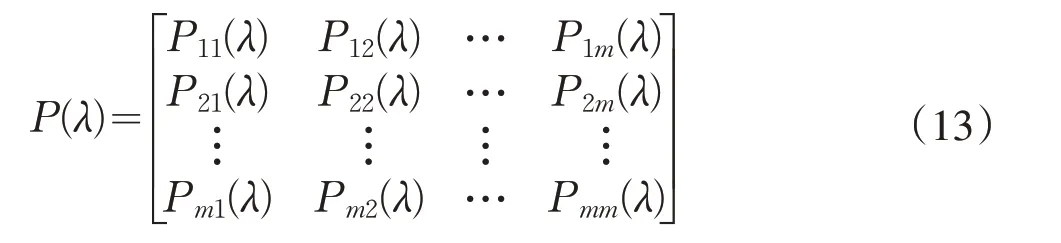
假定( π1(k),π2(k),…,πm(k))为状态概率分布向量，πj(0)为初始状态概率，利用此状态概率分布向量和状态转移概率矩阵可估算未来任一时期所处状态和预测值。第k+1期预测值可表示为［21］：

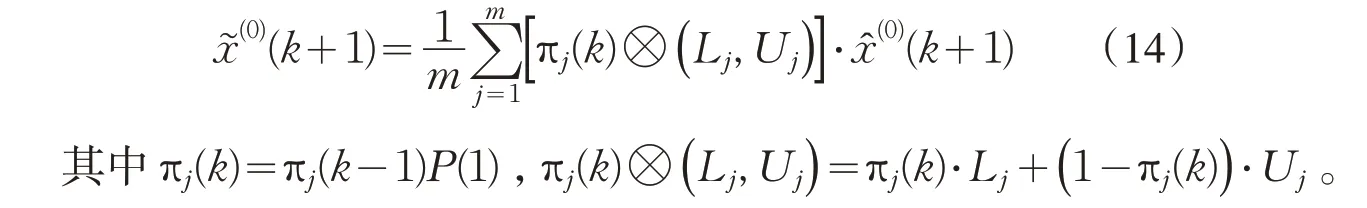
带时间幂次项的灰色马尔可夫预测模型流程如图1所示：

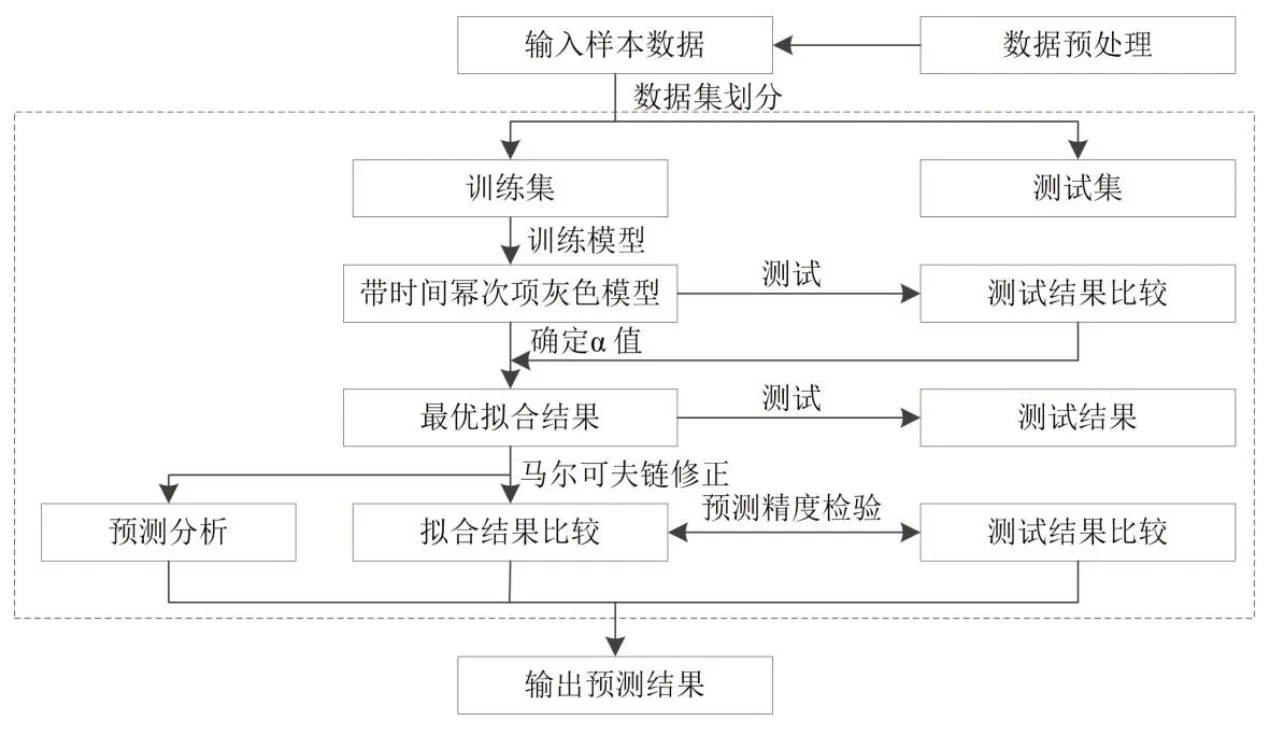
图1 带时间幂次项的灰色马尔可夫预测模型流程

1.3 预测误差度量指标

为合理评价模型的预测能力，需要量化预测误差。本文参照常用的相对误差（Relative Per⁃centage Error,RPE）、平均绝对误差百分比（Mean Absolute Percentage Error,MAPE）以及均方根误差（Root Mean Squared Error,RMSE）作为模型预测能力的测度指标，计算公式如下：

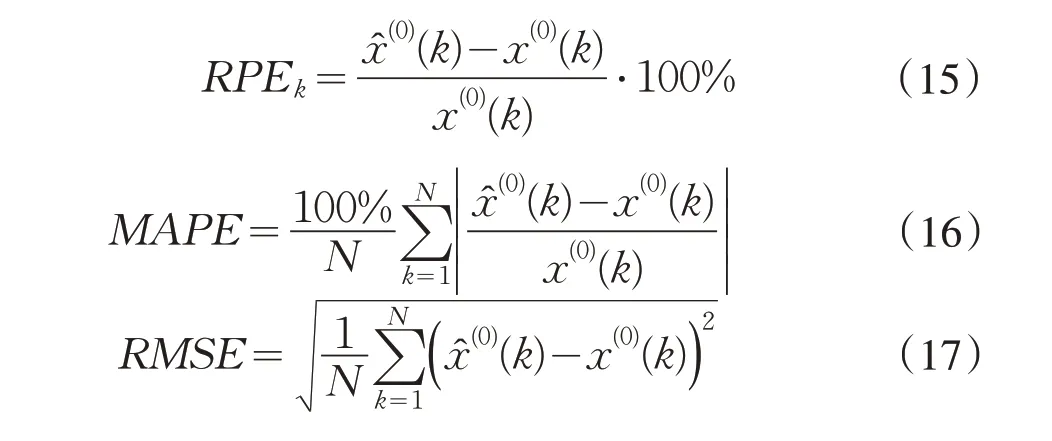
2 模型应用

为了分析带时间幂次项的灰色马尔可夫模型是否能够提升对中国能源强度的预测能力，本文选取了在预测中得到广泛应用的灰色GM(1,1)和带不同时间幂次项的GM(1,1,tα)(α=1,2)进行了相同的预测，旨在对不同模型的预测能力进行对比分析。

2.1 研究设计

2.1.1 问题描述与指标选取

为了验证所提出的模型在预测问题中的有效性和可操作性，本文对中国能源强度指标单位产值能耗进行预测，该指标计算公式为能源消费总量（吨标煤）/GDP（万元），用A表示。利用灰色GM(1,1)模型，带时间幂次项的GM(1,1,t)和GM(1,1,t2)进行对照分析，从中提取出最优α值，以此来构建经马尔可夫链修正后的GM(1,1,tα)模型，并评价其预测精度表现。

本文将样本区间设置为1995—2020 年，其中以1995—2018 年数据作为训练集训练模型，2019—2020年数据作为测试集用于预测不同模型的预测性能，并对2021年指标值进行预测。

首先利用自然对数变换对原始数据进行平滑性处理。

2.1.2 参数α的确定

将α取值分别设定为0,1,2，获得三个灰色模型GM(1,1)、GM(1,1,t)和GM(1,1,t2)，利用MATLAB软件（R2010a版）分别对各模型进行算法实现，获得lnA的拟合预测值后，再通过逆自然对数转换为原值。三个模型关于A在1995—2020 年的拟合结果趋势如图2所示：

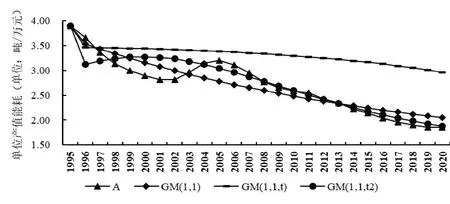
图2 不同时间幂次项下灰色模型的拟合预测值与真实值

通过比较可以发现，无论是从预测结果与实际值的拟合程度看，还是从整体变化趋势状况看，GM(1,1,t2)整体上拟合值较为接近真实值，拟合效果最佳。其次是GM(1,1)，表现最差的是GM(1,1,t)，与真实情况存在明显的差异。利用上述的RPE误差度量指标分别对三个灰色模型的预测性能进行定量考查，获得计算结果如表1所示：

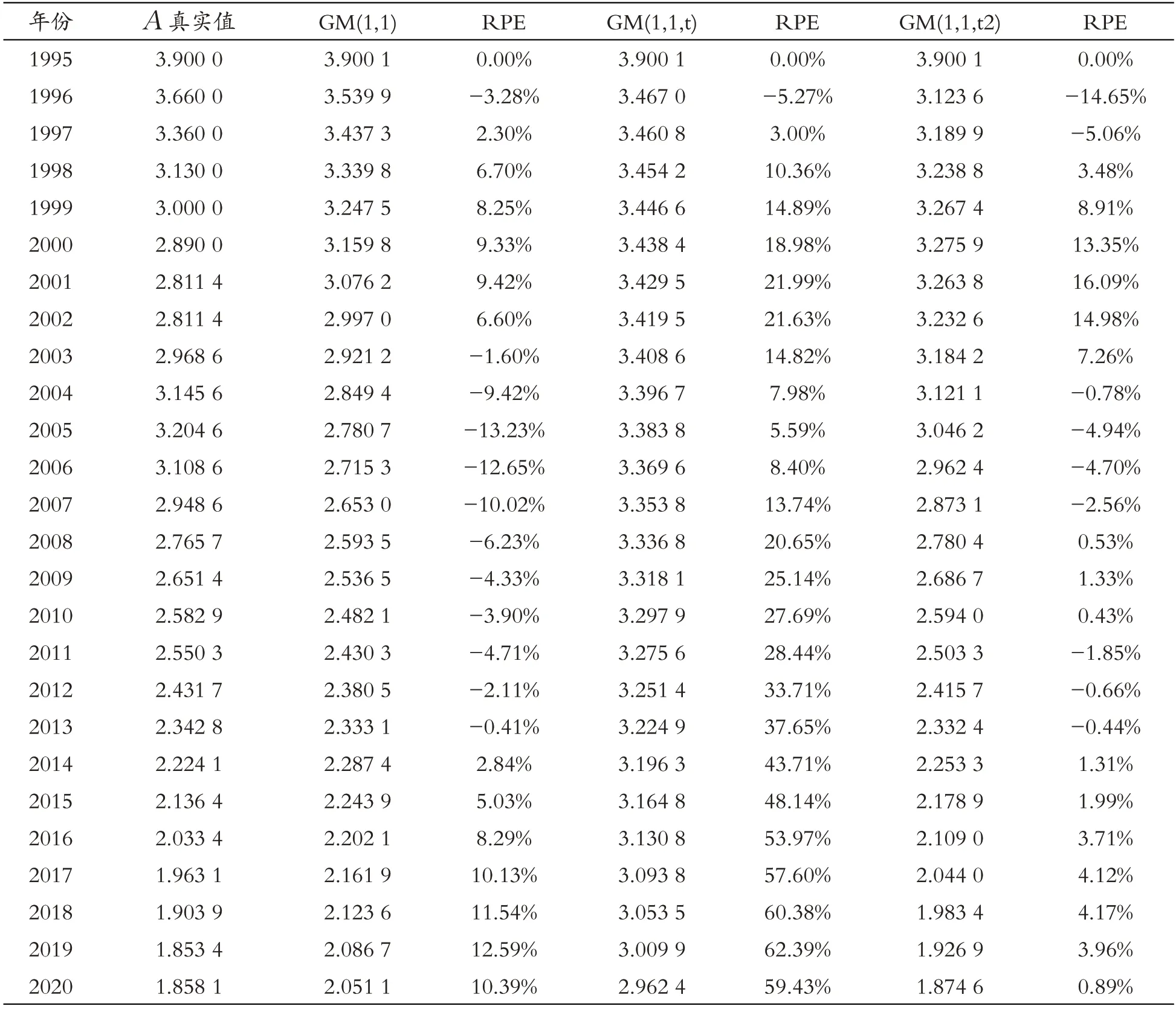
表1 不同时间幂次项下灰色模型的拟合预测结果比较

从表1测算结果表明，除个别年份以外，大部分年份GM(1,1,t2)模型的RPE 值均小于GM(1,1)和GM(1,1,t)。同时，可计算出GM(1,1,t2)的MAPE 指标在训练集和测试集上的数值分别为4.89%和2.43%，RMSE指标在训练集和测试集上的数值分别为0.209 7 和0.053 2，在三个模型中均为最低。这说明GM(1,1,t2)预测性能要优于其他两种模型，也反映了在对单位产值能耗A的预测中，参数α在可能取值为0,1,2情况下，带时间二次幂项的灰色模型预测性能最优。

2.1.3 带时间幂次项的灰色马尔可夫模型预测

利用GM(1,1,t2)模型计算出1995—2018 年单位产值能耗对数值lnA的拟合值，以拟合值与真实值比例构建比率序列{s(k)}，根据比率序列的具体数值，按照公式（10-11）将之划分的马尔可夫状态区域为：第一，Q1状态界限为[ 0 .8779,0.9667)，属于预测偏低情形；第二，Q2状态界限为[0.9667,1.0555)，属于预测适中情形；第三，Q3状态界限为[1 .0555,1.1444]，属于预测偏高情形。并以此将训练集中每年的比率值进行分类，得出如表2所示的预测拟合状态汇总表：

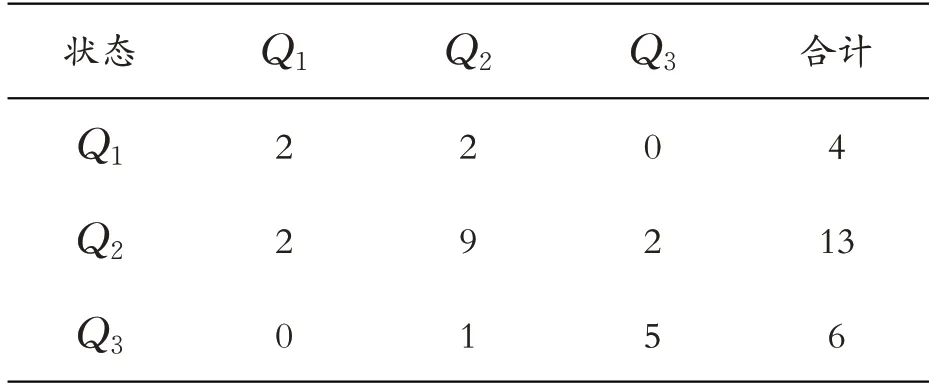
表2 预测拟合状态汇总

按照上述分类汇总情况，可得到一步转移概率矩阵为：

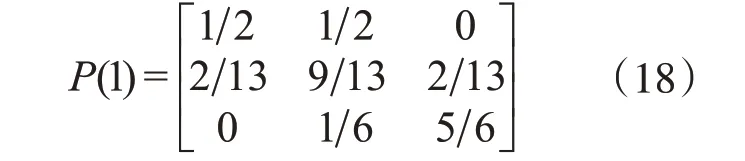
根据马尔可夫链的预测原理，由P(1)获得λ步转移概率矩阵P(λ)，基于训练集的样本数据和GM(1,1,t2)的拟合结果，利用公式（14）和逆自然对数转换可计算出2019—2020年的拟合结果，经马尔可夫链修正后的GM(1,1,t2)模型的RPE 绝对值均小于GM(1,1,t2)，预测精度得到进一步提升。具体结果如表3、表4所示。

表3 带二次时间幂项的灰色马尔可夫模型预测结果

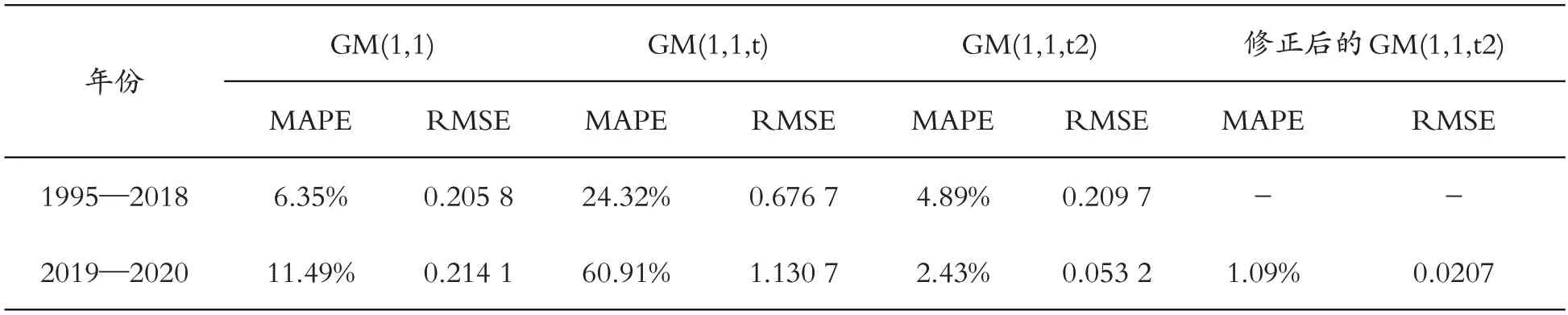
表4 四种模型的预测精度比较

2.2 预测精度检验

从表3 和表4 可以看出，首先，经马尔可夫链修正后的GM(1,1,t2)预测模型无论是RPE（相对误差），还是MAPE（平均绝对误差百分比）检验以及RMSE（均方根误差）检验，均一致优于其他三种模型，这说明在对单位产值能耗对数值lnA的预测中，带时间二次幂项的灰色马尔可夫模型预测精度最高，整体上优于其他三种灰色预测模型。其次是GM(1,1,t2)模型，预测精度最差的是GM(1,1,t)，在训练集年份MAPE 超过了20%，测试集年份MAPE 则高达60.91%，从拟合度和变化态势上均与现实情况存在明显偏差，这说明其不适宜用来对中国历年单位产值能耗变化进行拟合预测。

2.3 预测结果与分析

分别应用上述四个模型对2021 年反映中国单位产值能耗对数值进行预测，利用逆自然对数变换为标准预测值，并汇总测试集2019—2020年的预测结果以便于比较，具体如表5所示。

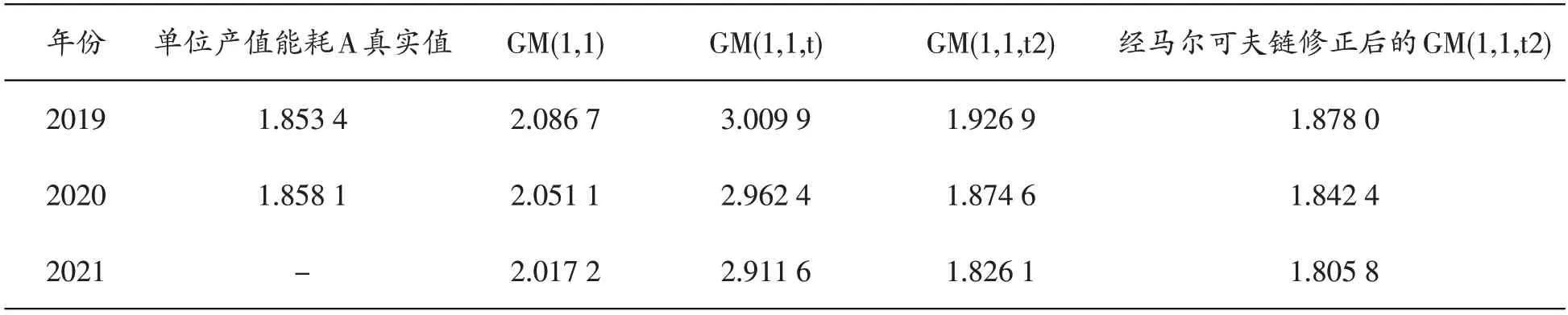
表5 2021年中国单位产值能耗预测值（单位：t/万元）

灰色GM(1,1,t2)模型预测曲线与中国单位产值能耗原始数据的趋势大致相同，可以较好地拟合中国单位产值能耗的变化态势。带时间二次幂项的灰色马尔可夫模型通过转移概率矩阵对灰色GM(1,1,t2)模型进行修正，得到了更为接近真实值的结果。按照预测精度=1-| |RPE的计算公式，其在2019 和2020 年的预测精度进一步提升至98.67%和99.15%。这表明了所提出的预测方法的科学性和合理性。同时，根据样本数据可以合理预测2021 年中国单位产值能耗为1.805 8 t/万元。

3 结语

本文提出了一种新的带时间幂次项的灰色马尔可夫预测模型。基于中国1995—2020 年单位产值能耗数据序列进行了数值预测，并与传统灰色GM(1,1)模型和带时间幂次项的灰色GM(1,1,tα)(α=1,2)模型进行了比较分析。实验结果发现：第一，在灰色模型中，带时间二次幂项的GM(1,1,t2)的预测精度最高，拟合曲线趋势与实际情况较为吻合，预测效果最好；其实是灰色GM(1,1)模型；带时间一次幂项的GM(1,1,t)模型预测值严重偏离真实值，预测效果最差。第二，在灰色GM(1,1,t2)模型预测的基础上，借助马尔可夫链在无后效性事件预测上的优势，利用转移概率矩阵对GM(1,1,t2)的预测结果进行修正，修正后精度得到进一步提升，能更准确预测中国能源强度的变化趋势，据此估计未来一年中国单位产值能耗数值。

总体来说，带时间幂次项的灰色马尔可夫模型集成了灰色GM(1,1,tα)模型，在有限样本下的预测性能和非指数变化规律刻画能力，以及马尔可夫链针对预测结果的校准能力。根据样本序列指数或非指数变动规律的问题特征选择时间最优幂次项，并利用马尔可夫链对预测结果进行校正以缩小其偏差，这使其预测精度更高且应用场景更为广泛。但需要指出的是，对单位产值能耗的中长期预测中，通常会受到更多不确定因素的影响。在实践过程中，有必要在该模型基础上适当附加其他条件，以弥补单一数据序列的缺陷，提高中长期预测的准确性。