基于分区标准化数据处理的路面抗滑性能影响因素分析

曾 诚

（四川省公路规划勘察设计研究院有限公司，四川 成都 610041）

1 数据来源

文章数据来源于LTPP SPS-3 数据库。长期路面性能（LTPP）计划是一项美国和加拿大用路面进行了20年的研究。它的目标是通过使用不同材料和在不同因素下（如降水、交通、温度、路基土或养护措施）的各种路面结构设计来延长路面的使用年限。LTPP计划中的特定路面研究实验（SPS-3）是在1990年设计的，用来评估养护方案的有效性，并确定适用于柔性路面的经济有效的养护处理方法。它提供了大量的数据，可以用来分析养护对路面性能的有效性。在LTPP项目中，共有81个SPS-3站点分布在美国和加拿大。在这些站点中，有53个站点提供了摩擦监测数据，在每个现场，除控制段外，在平均长度为500英尺的路面段上，连续进行四种养护处理（薄层罩面、稀浆封层、裂缝密封、碎石封层），因此，经过养护处理的路面段与控制段具有相同的气候和交通条件。为了考虑影响路面性能的主要设计因素，将LTPP试验场地具体分为11类，划分类别的设计因素包括气候（降水和温度）、路面结构（路基类型和现有路面状况）和LTPP项目定义的交通荷载。

2 沥青路面抗滑性能影响因素

在路面干燥的情况下，轮胎与路面之间接触状态最好，摩擦系数最高，抗滑性能也就最好。此时，光滑路面和粗糙路面的抗滑性能接近，摩擦系数差值很小。在路面潮湿的情况下，轮胎与路面之间不能直接接触，会相隔一层水膜，破坏了应有的黏附力，车辆会发生滑溜现象，沥青路面的抗滑性能会显著降低。路面温度对沥青路面的抗滑性能也有着很显著的影响，当温度过高时，沥青会发生软化，路表颗粒会因车辆的作用而下陷，从而导致路面摩擦系数降低。在结冰路面，温度在0 ℃附近时，路面会产生冰水混合物而导致路面摩擦系数有明显的降低。

当车辆在路面行驶时，轮胎胎面与胎面和路面的接触位置产生相对位移。这将会造成路面骨料颗粒的磨损、脱离和下沉，粘合剂材料将会包裹骨料，减少了细构造的暴露面积，从而影响了路面的抗滑性能。随着交通量和交通荷载的不断增加，粘合剂材料不断地被带到路表与轮胎接触。这会导致轮胎的扭矩不断增加，从而轮胎与路面的剪切力会不断增大，而这种剪切力会导致路表的颗粒脱落或者下沉，从而改变了路面的宏观构造，降低了路面的抗滑性能。同时局部的摩擦会磨光路面骨料颗粒，从而改变路面的微观构造，减小了路面的摩擦系数，降低了路面的抗滑性能。

通过美国和加拿大用路面进行了20年研究的LTPP SPS-3 数据库，可以得知路面的年龄、路段所在地区的年平均降雨量、年平均冻结指数、年平均湿度、年平均温度、交通荷载、年平均日交通量、年平均日货车交通量、疲劳开裂程度都会对沥青路面的抗滑性能产生影响。

3 沥青路面抗滑性能影响因素分析

通过对沥青路面抗滑性能影响因素的初步分析可以得知路面的年龄，路段所在地区的年平均降雨量、年平均冻结指数、年平均湿度、年平均温度、交通荷载、年平均日交通量、年平均日货车交通量、疲劳开裂程度都会对沥青路面的抗滑性能产生影响。现分别对各项指标进行单独一元线性回归分析，得到表1，表2如下：

表1 各项因素与摩擦系数的相关性

表2 各项因素与摩擦系数的相关性

从表中数据都远远小于1可以得出，这些因素与沥青路面的抗滑性能都没有单独的相关性，可能是所使用数据的量级不够而导致的。为了探究这些因素对沥青路面抗滑性能的影响应将它们与沥青路面的抗滑性能进行多元回归分析。

4 沥青路面抗滑影响因素模型的建立

根据上文可知，沥青路面的抗滑性能受多种因素的影响，但根据各因素对沥青路面抗滑性能的各自的相关性可知，它们与沥青路面的抗滑性能均无单独强烈的相关性，但路面的抗滑性能又确实受这些因素的影响。因此对沥青路面抗滑性能的影响因素进行多元线性回归分析，并会建立相关模型。

4.1 模型的建立

影响路面抗滑性能的影响因素有很多，现根据LTPP SPS-3 数据库中数据，选取13个因素，分别为路面初始摩擦系数（X1）、路表处治方法（X2）、路面年龄（X3）、地区年平均降雨量（X4）、地区年平均温度（X5）、地区年平均冻结指数（X6）、地区年平均湿度（X7）、年平均日交通量AADT（X8）、年平均日货车交通量AADTT（X9）、交通荷载（X10）、疲劳开裂面积（X11）、车辙深度（X12）、路面平整度（X13）。初步建立模型方程：

4.2 回归方法的确定和思路

根据相关资料可知，选取的13个因素之间会有因素两两之间互相影响。比如说，地区年平均降雨量与地区年平均湿度很明显就会有影响，地区的年平均温度对地区年平均冻结指数也会产生影响，地区的年平均日交通量、年平均日货车交通量、交通荷载会对疲劳开裂面积、车辙深度、路面平整度均会产生影响。为了消除这些共线性对回归模型的影响，本文将采用逐步回归的方法来对沥青路面的抗滑性能影响因素进行多元回归分析。

逐步回归分析方法的基本思路是在建立多元线性回归方程的时候，会逐步进行相关因子的挑选，即每运行一步进行一个因子的挑选。第一步要计算所有因子的方差贡献，选用还没有引进的因子中方差最大的因子在给定的置信度下进行F检验（即引进检验）。如果这个因子能通过F检验，则引进这个因子；如果这个因子没有通过F检验，则不引进这个因子。在引进两个因子之后，计算剩下的m-2个因子的方差贡献，选用其中方差最小的因子在给定的置信度下进行F检验（即剔除检验）。如果这个因子通过了这个剔除检验，则该因子会被剔除。当回归方程不能再引进或者剔除新的因子的时候，逐步回归也就结束了。

4.3 SPSS软件分析结果

经过上述操作之后，SPSS软件会自动对数据进行分析，并输出结果。此次分析共得到9个模型，选取因变量Y与选择使用的9个因变量（X1、X2、X3、X4、X5、X6、X7、X8、X9）之间的相关关系最好的模型，起调整后的值为R2=0.553。

用F函数对最佳模型建立的多元线性回归方程进行拟合优度检验如下表3，可以得到显著性检验值F=111.824。回归和残差的自由度为9和1408。在给定显著性水平α=0.01的前提下查F（f1，f2）检验表得知F（9，1408）=2.41＜111.824=F，且在F=111.824时，相伴概率p=0.000＜0.01。这些可以说明此线性回归分析显著，在统计学上有意义，表明路面的抗滑性能与这些选定的因素有显著的线性关系。

表3 模型拟合优度检验表

模型的回归系数如下表4所示。该模型的常数C=20.555，回归系数为β1=0.582、β2=-0.820、β3=-0.164、β4=-0.004、β7=0.140、β8=0.001、β9=-0.003、β12=-0.102、β13=-0.826。经过t检验，X7的回归系数的相伴概率为p=0.001＜0.05，的回归系数的相伴概率p=0.039＜0.05，X12的回归系数的相伴概率p=0.008＜0.05；其他项的回归系数的相伴概率都为p=0.000＜0.05，则可以判断，该模型通过了显著性t检验，表明回归系数在统计学上有意义。

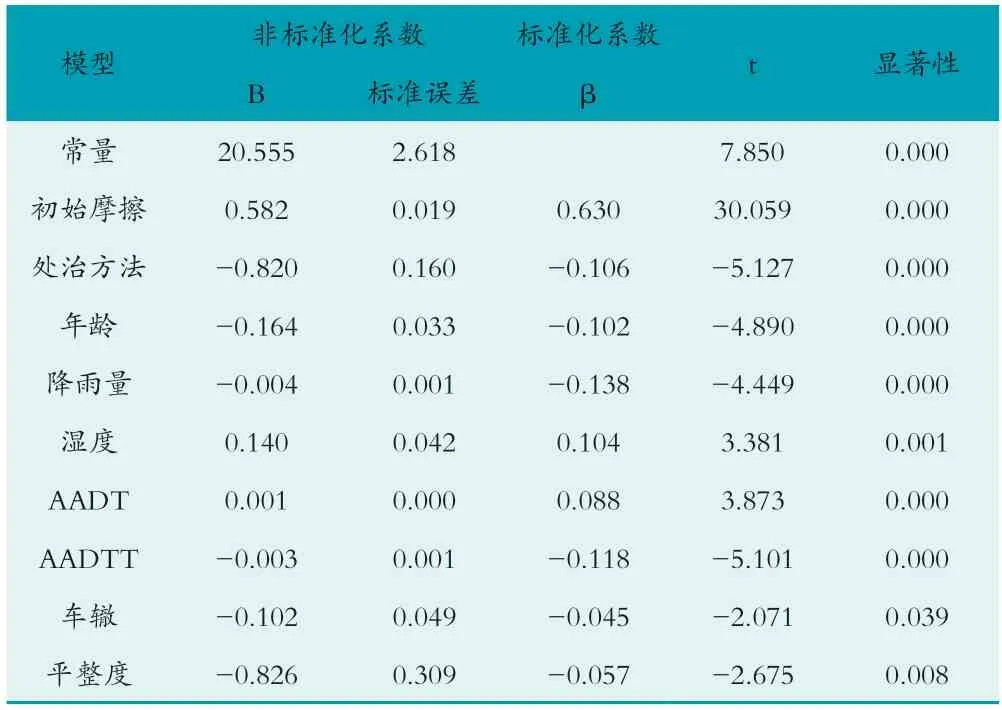
表4 回归系数

4.4 模型确定与分析

经过上述研究分析后，可以确定最终的模型公式为：

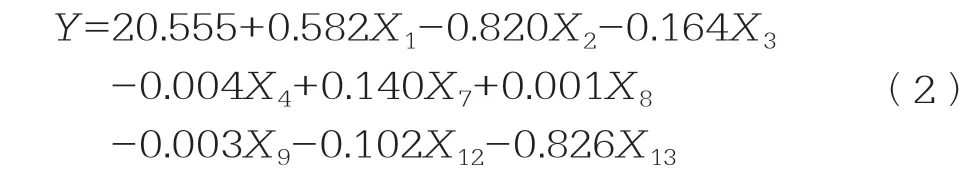
式中：Y—路面摩擦系数

X1—路面初始摩擦系数

X2—路面处治方法

X3—路面年龄（年）

X4—地区年平均降雨量（mm）

X7—地区年平均湿度（%）

X8—AADT（辆/日）

X9—AADTT（辆/日）

X12—车辙深度（mm）

X13—路面平整度（m/km）

式中所采用的路面抗滑性能的影响因素可以被判定为对沥青路面抗滑性能影响最显著的因素，当路面年龄、年平均交通量比较大时，路面的累计交通量和受到的损害程度会随之增大，但不同路面处治方法对减小路面受损的程度不同。而且路面的车辙深度和平整度会受到累计交通量的增大而变化，当路面出现车辙和平整度降低时，路面上都会出现凹槽，在降雨量和湿度较大的地区凹槽会产生积水现象，通过的车辆会发生漂滑现象，路面的抗滑性能会降低。

5 结语

沥青路面的抗滑性能会受到养护处治方法、路面的年龄、路段所在地区的年平均降雨量、年平均冻结指数、年平均湿度、年平均温度、交通荷载、年平均日交通量（AADT）、年平均日货车交通量（AADTT）、疲劳开裂程度、车辙深度、路面平整度的影响。由于本文的数据来源为LTPP SPS-3数据库，该数据库在统计时选用的路段较多，且路面的养护方法、所处环境、交通因素各不相同，则对单项影响因素进行分析时无法排除外在因素的影响，从而导致沥青路面抗滑性能与各影响因素的相关性不高。文章对沥青路面抗滑性能进行多元回归分析时采用的是逐步分析法，则可以分析出路面的养护处理方法、路面的年龄、路段所在地区的年平均降雨量、年平均湿度、年平均日交通量（AADT）、年平均日货车交通量（AADTT）、车辙深度和路面平整度对沥青路面抗滑性能的影响更为显著。而且这个方法的建模过程简单方便、输出结果比较直观、精确度比较高，可以大幅度减少计算时间。文章建立了沥青路面抗滑性能与多种影响因素的多元回归方程，当样本更加充足而且典型性和代表性更加强烈时，可以得到更加精确的结果。