非线性范畴微气压波快速预测模型

韦 斌,唐 飞，谭晓明,2,3

(1.合肥工业大学 汽车与交通工程学院，合肥 230009； 2.中国空气动力研究与发展中心 气动噪声控制重点实验室，四川 绵阳 621000；3.湖南理工学院 机械工程学院，湖南 岳阳 414006)

高速列车在穿越隧道时挤压前方空气并形成压缩波，其中第一道压缩波被称为压缩头波。压缩头波传递到隧道出口并向周围辐射低频脉冲波，可在近场产生高达140～150 dB空气爆鸣声音，称之为微气压波。该现象在武广线、兰新线、京沪线等线路的200～350 km·h-1高速列车隧道空气动力学试验中均得到发现，微气压波容易导致隧道结构破坏，产生的脉冲噪声也是严重的环境问题，因此对产生的微气压波进行预测和采取措施十分必要。微气压波的大小与到达出口处的压缩波压力梯度成正比[1]，现较多采用在隧道入口处安装通风罩[2-3]并对列车头进行优化[4-6]等措施降低压缩波的压力梯度，进而减小微气压波。

诸多学者对微气压波展开了模型研究。在目前的工作中，压缩波的形成通过经验公式[7]来预测，该公式使用了列车速度和阻塞比等参数，但对压缩波的形成起着重要作用的车头形状并没有考虑。Howe[8-9]利用精确的声学格林函数分析了半无限和圆筒形隧道的压缩波。Miyachi[10]基于边界积分方程提出了可以预测微气压波效应的模型，但模型中的格林函数需要有分析解。文章将在文献[1]提出的微气压波计算模型基础上进行改进，提出具有工程应用价值的参数化微气压波计算模型。

微气压波的大小随着列车速度的增加而增加，随着高速列车运行速度的提高需要更准确地预测微气压波。当高速列车以200～250 km·h-1速度进入隧道时，隧道出口10 m位置的微气压波峰值数量级为10 Pa。该波为拟线性波，在拟线性范畴内，可用经典线性理论较好描述其机理和传播特性，并相对有效地分离各种关联因素，从而构建简化的快速预测模型(如文献[1]中Yamamoto提出的微气压波计算模型)，但这些模型的应用大都局限在线性范畴。随着高速列车穿越隧道速度增大到350 km·h-1时，隧道出口10 m位置微气压波峰值数量级可达102Pa，其波形近似于三角波[11]，而三角波属于典型的非线性波。这表明在近隧道口区域形成了较强的非线性声源区，且其非线性随着高速列车穿越隧道速度的增大而增强。文献[11]指出Yamamoto微气压波计算模型的计算结果与试验结果的相对误差可达20%。目前我国正在研发400 km·h-1的新一代高速列车[12]与600 km·h-1的超高速磁悬浮列车[13]，届时微气压波的非线性特性将近一步增强，这将对目前简化的快速预测模型提出更高挑战。

尽管目前微气压波的计算还包括滑移网格[14-16]、动态分层网格[17]、重叠网格[18]、流(声)场解耦[19-20]等方法，但这些方法难以保证时空离散格式与插值格式精确求解微气压波的传播过程，更难获取近隧道出口区域微气压波的准确波形。另外，这些方法消耗的计算资源巨大，因此，探讨非线性范畴微气压波快速预测模型，有利于高速铁路隧道口微气压波的评估和防治。

1 微气压波试验

微气压波试验是在中南大学动车组空气动力特性动模型试验平台完成。本试验使用了两种类型传感器，分别是压力传感器和丹麦B&k公司的4193传声器。压力传感器安装在距离隧道出口适当位置的隧道壁面，用于采集压缩头波的试验结果；4193传声器安装在距隧道出口10 m和20 m的轴向距离位置(全尺寸)，用于采集微气压波的试验结果。该试验可为微气压波数值计算模型提供压缩头波数据，并验证参数化微气压波的计算公式正确性。

表1列出了试验工况及试验结果，图1展示微气压波的原始与滤波处理的时间历程曲线。由图1可知，随着列车运行速度增大，微气压波波形逐渐趋向三角波，尤其在350 km·h-1时其波形近似为三角波，且其幅值数量级可达102Pa。这是因为微气压波形近似于第1道压缩波波前梯度的波形，而第1道压缩波波前梯度随着列车运行速度的增大而增大。

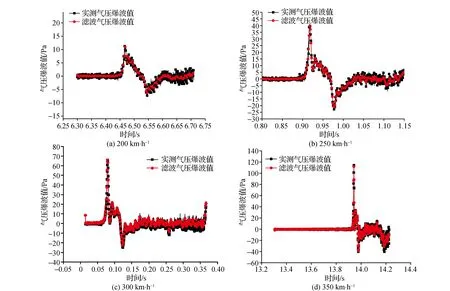
图1 隧道出口10 m位置微气压波及滤波时间历程曲线

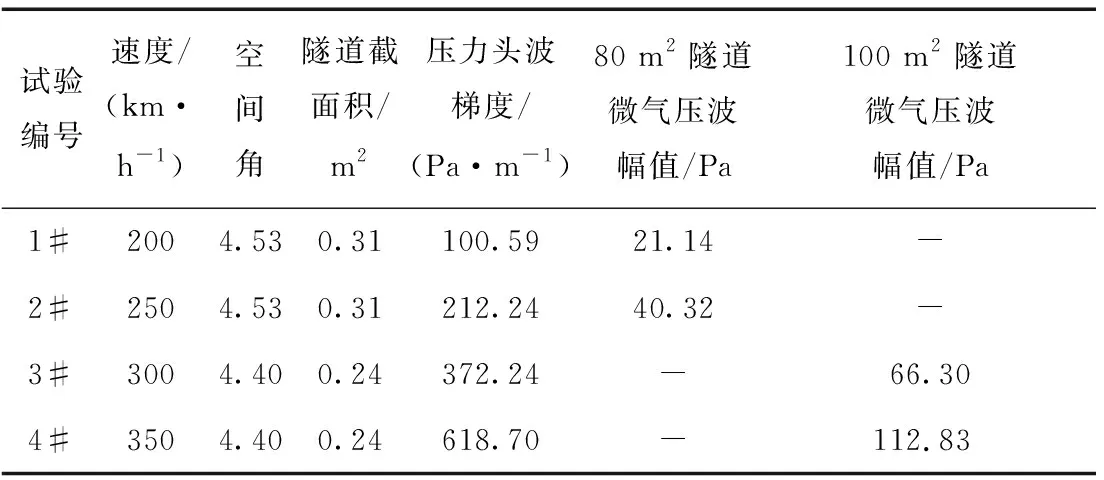
表1 微气压波原始数据

2 微气压波参数化预测模型

对于强非线性微气压波问题，管道出口大约2倍直径区域内都属于气动声源区[21]。当高速列车穿越隧道速度级高于300 km·h-1时,隧道出口2倍直径区域内均为气动声源区。在该区域内，根据Yamamoto的微气压波计算模型进行改进，并引入参数α，算式为

(1)

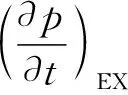
通过动模型试验获取压缩头波数据，再用高阶谱差分技术数值模拟隧道出口微气压波波形，获取隧道出口轴向不同位置的微气压波峰值，并利用幂函数模型拟合微气压波峰值与隧道出口轴向距离的函数关系，可得到参数α大小。

3 微气压波数值计算模型

隧道属于类似圆管的轴对称结构，另外，微气压波波长较短,可忽略隧道出口的轨道反射，将隧道简化成圆管结构，再将微气压波数值结果进行面积校正。由于隧道及出口具有轴对称性质，微气压波数值计算模型可简化为2维。通过在圆管中添加压力头波，在隧道进出口根据需要设置相应边界，然后通过CAA数值模拟压力头波在圆管中传播及在隧道出口向外辐射过程(见图2)。

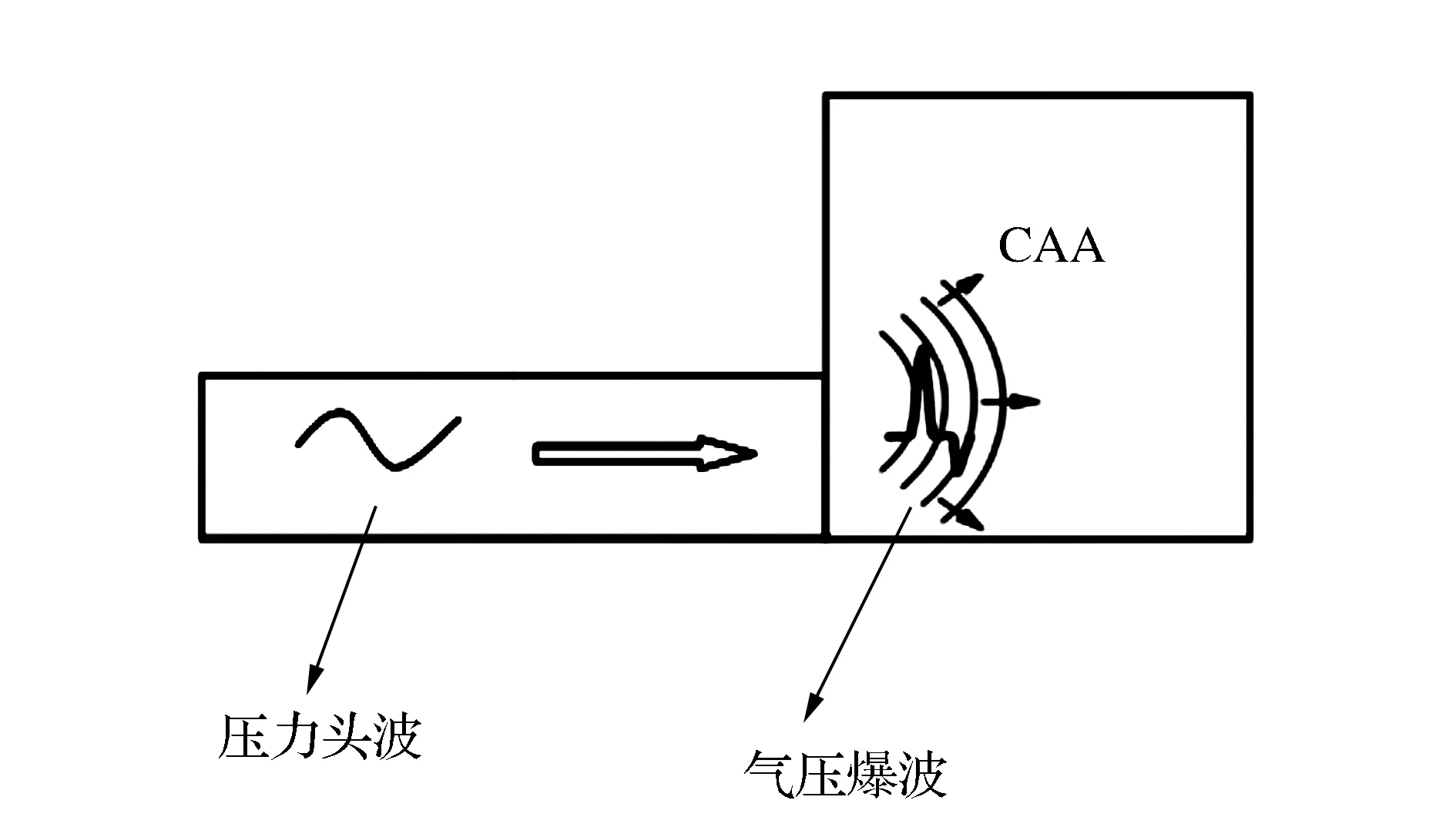
图2 微气压波物理问题描述

隧道内压缩头波的传播过程与隧道口外微气压波的传播过程均使用2维轴对称Euler方程作为主控方程，应用基于高阶谱差分的CAA方法[22]数值求解。主控方程在时间上采用5/6步、低频散低耗散龙格库塔(LDDRK)方法进行离散，在空间上采用四边形网格、3阶谱差分方法展开离散。该模型隧道壁面和出口端壁面采用固壁边界条件，计算域进出口采用PML[23]人工边界条件。

已有相关文献详细对该数值计算模型的边界条件展开数值校核，也对数值计算模型展开了试验校核，如文献[11]所述，计算的微气压波峰值误差在5%以内。

4 参数化预测模型数值研究

在线性范围内，微气压波声压峰值与r成反比；在非线性范围内，微气压波声压峰值与r不成反比。现利用一系列工况中的压缩头波数据，采用CAA技术数值模拟隧道出口微气压波波形，获取隧道口不同位置的声压峰值Pmic,max，拟合出Pmic,max与r的函数关系式。由于文中试验工况中有两种不同直径隧道，所以CAA需要采用两套计算网格，网格取该隧道直径(0.665 m和0.738 m)为特征长度,并作网格无量纲化处理，如图3所示。其中长度无量纲单位“1”表示隧道直径，边1、3、4、5为PML边界条件，边6、7为固壁边界，2为对称边界。CAA所采用的初始波来源于一系列工况中的压缩头波，如图4所示。

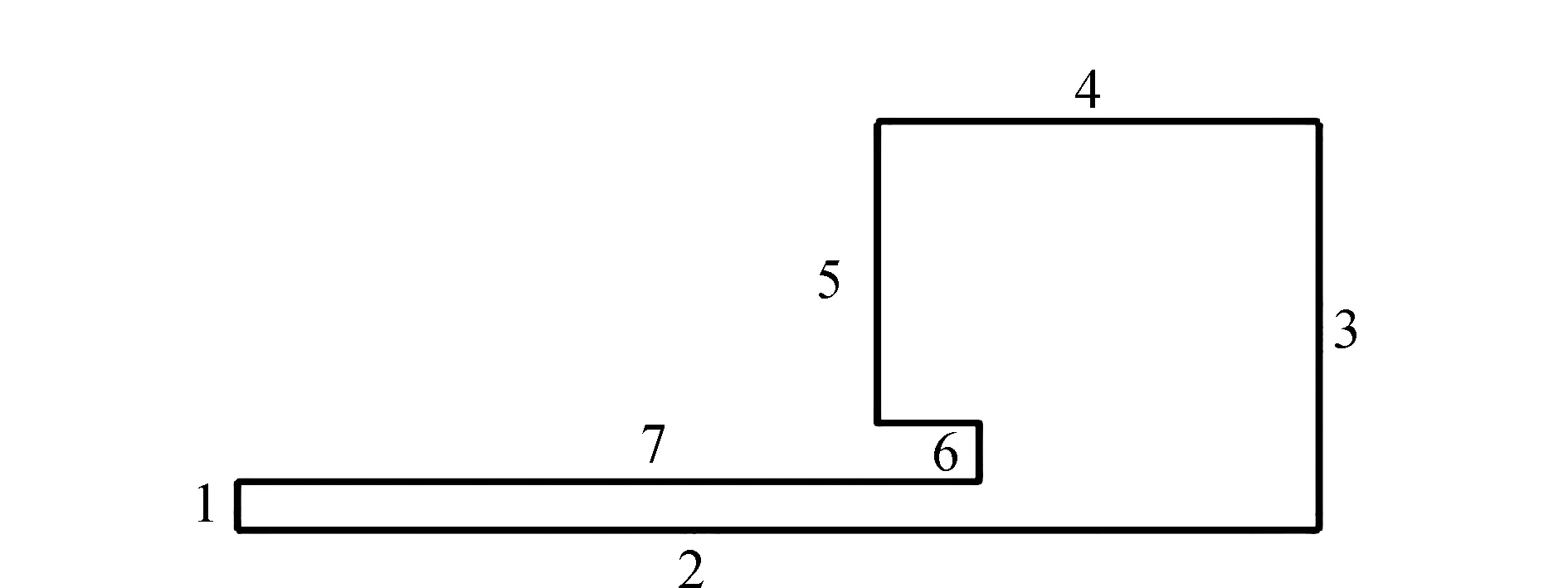
图3 计算网格

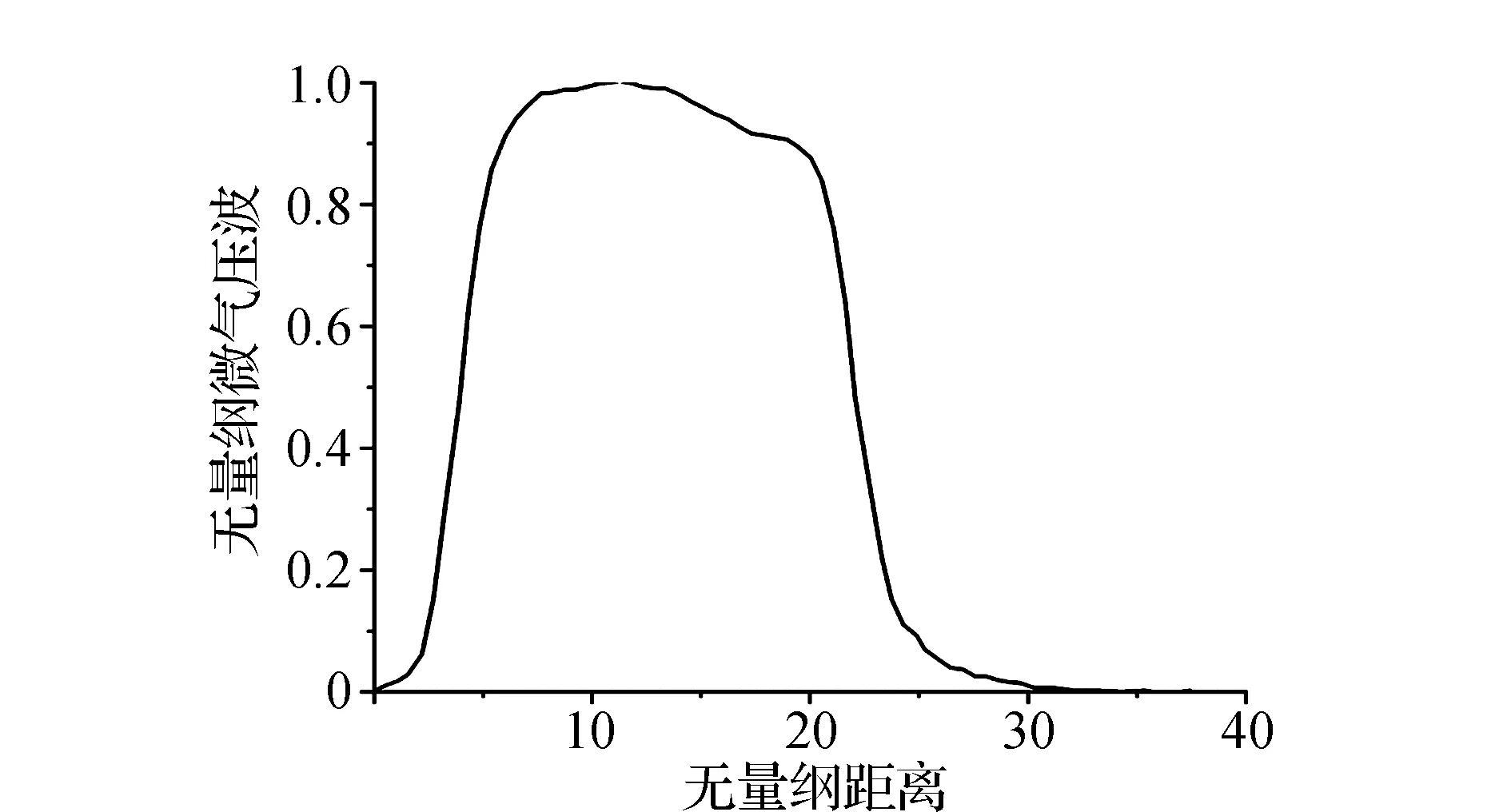
图4 初始波形

图5给出瞬态声压场分布。计算结果与试验结果对比曲线如图6、图7所示。

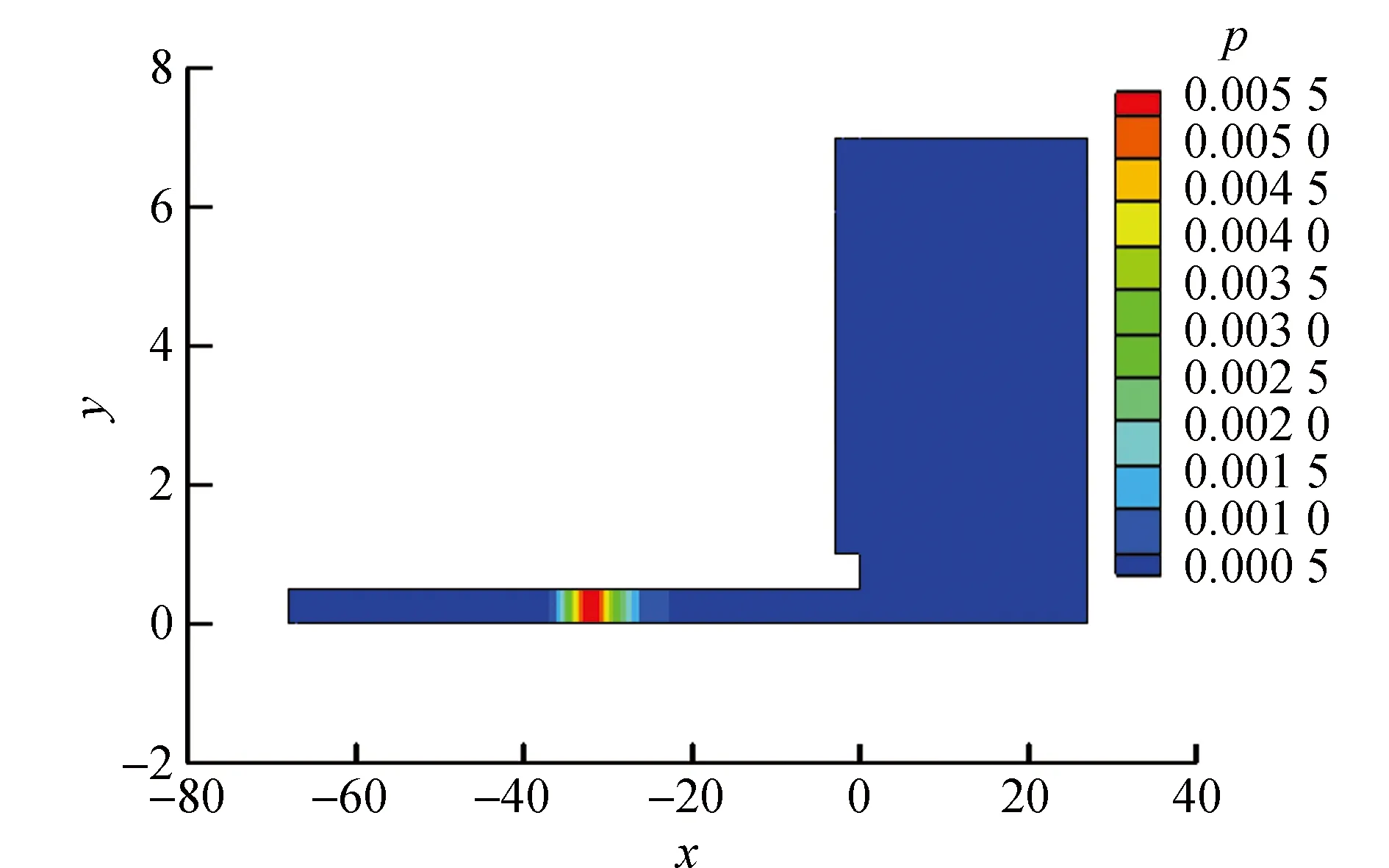
图5 瞬态声压分布

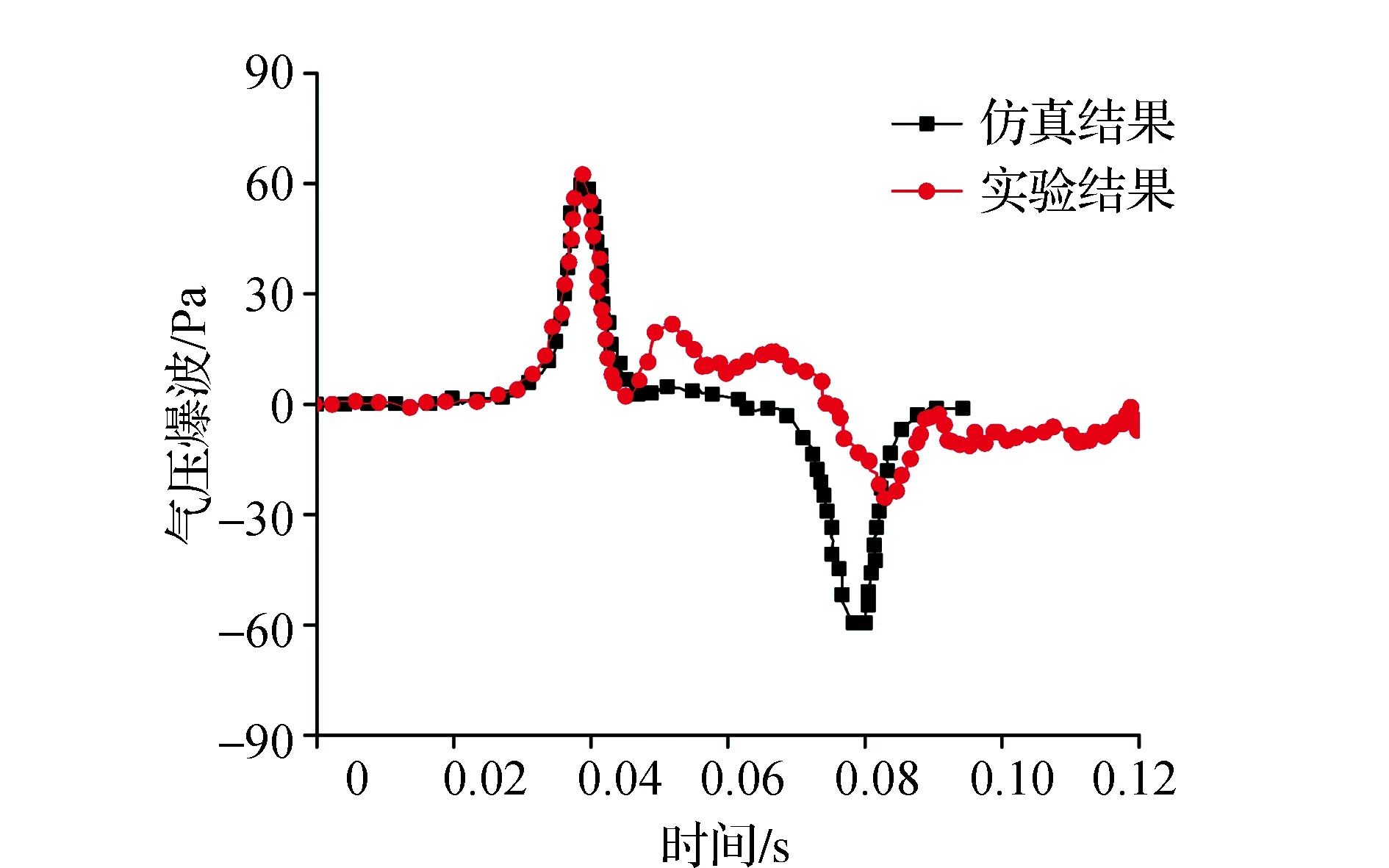
图6 300 km·h-1数值与试验结果比较

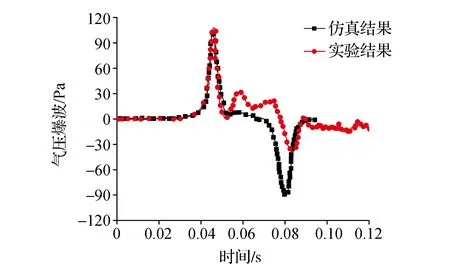
图7 350 km·h-1数值与试验结果比较

由图6、图7可知微气压波前半段的仿真与试验波形较为吻合，而其后半段波形吻合度较差。这是由于微气压波前半段波形几乎不受隧道外轨道、支架、地面等障碍物的阻碍和反射等因素影响，而其后半段波形受上述因素影响较大，但2维轴对称模型没有考虑上述影响因素。

在CAA中隧道出口对称轴上设置12个不同位置采样点，获取不同位置的声压峰值，进行幂函数拟合，拟合函数为y=axb，其中a、b为拟合参数，x为隧道出口轴向空间距离，y为声压峰值。其拟合结果如表2、图8所示。不同工况下所用车型均为某种高速列车车型的改进型。

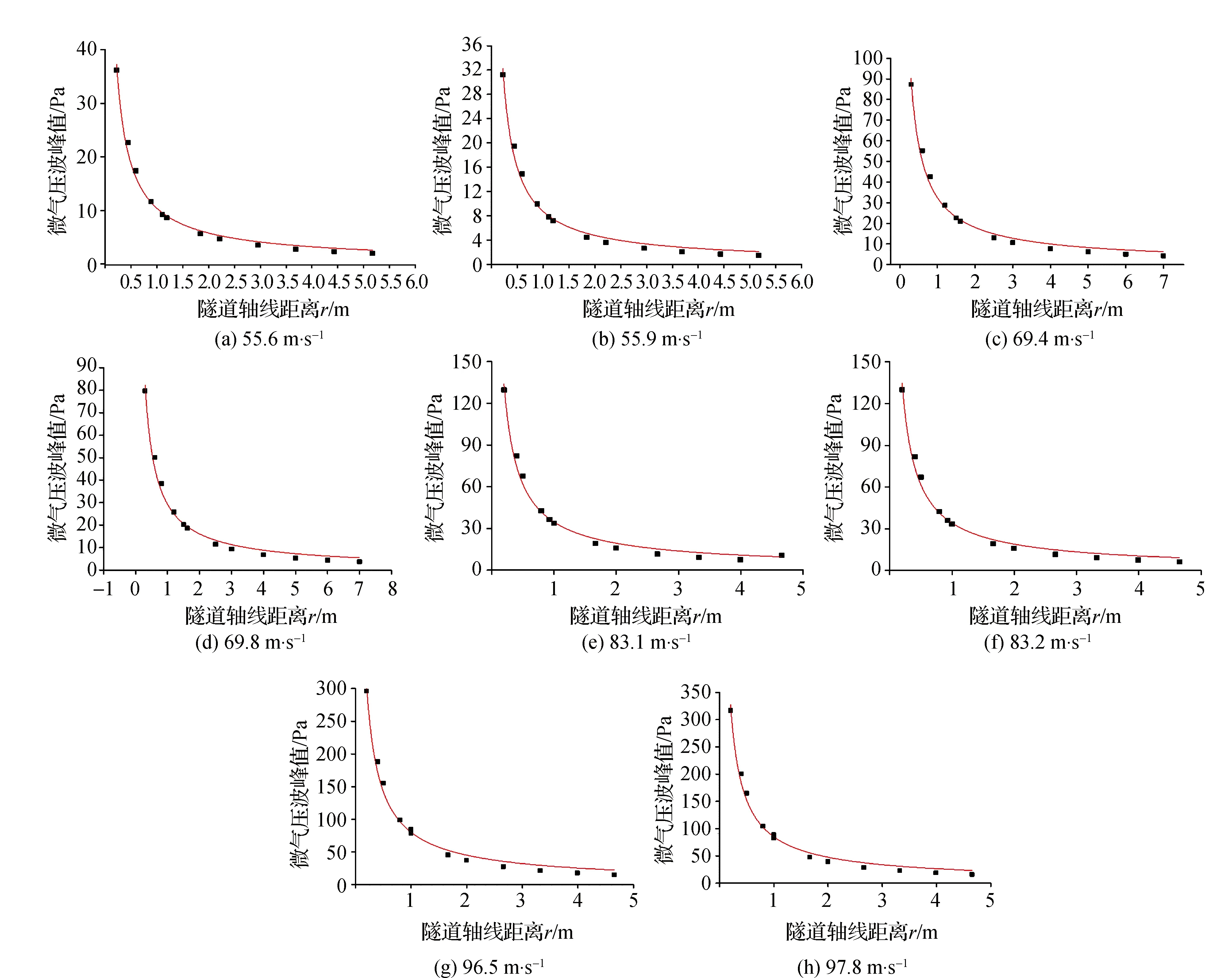
图8 Pmic,max与r拟合

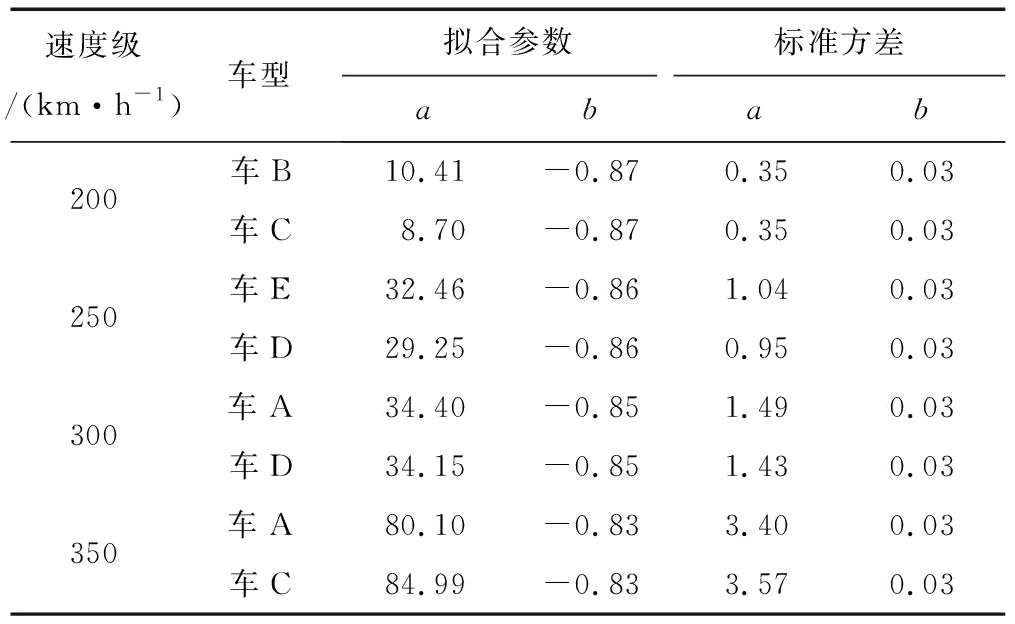
表2 Pmic,max与r拟合结果

5 参数化预测模型校核

对式(1)作调整得

(2)

对式(2)作调整得

(3)

式中:α取自表2。

将表1中数据分别代入式(2)和式(3)中，整理后如表3所示。

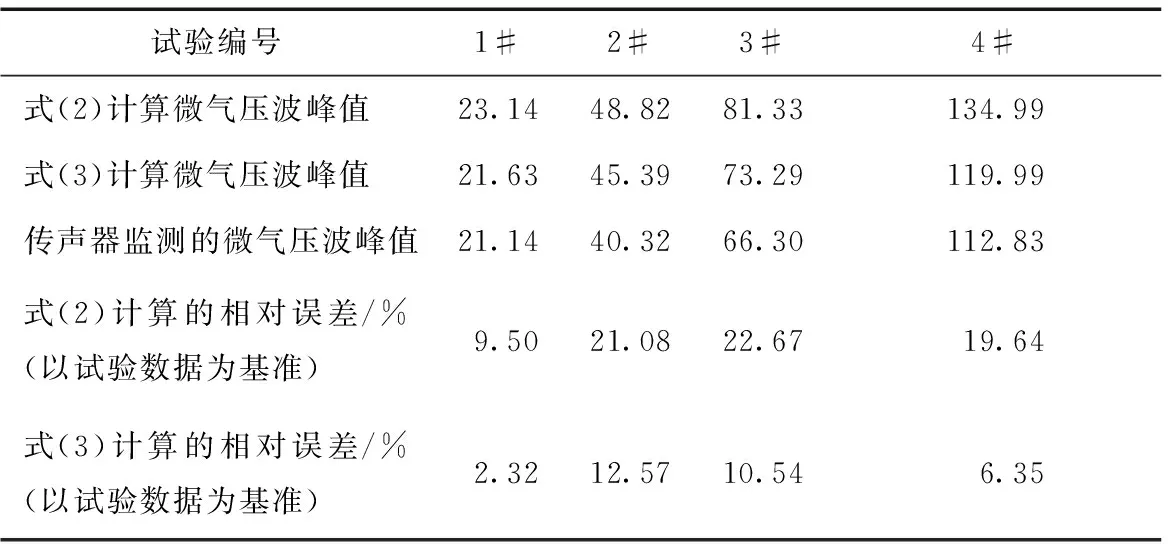
表3 预测模型校核

根据表3的计算结果，式(2)所计算的微气压波峰值的相对误差较大，难以满足工程应用要求。主要由于式(2)是在线性范围内推导得到，而当高速列车进入隧道的速度级达到200 km·h-1以上时，隧道出口1倍隧道直径范围内的空间属于气动声源区，为典型的非线性范畴，式(2)就不再适合计算这个区域的微气压波峰值。对于这个区域的微气压波峰值计算，随着高速列车进入隧道的速度级逐渐增加，即该区域微气压波的非线性逐渐增强，式(3)计算的相对误差越来越小，说明式(3)较适合计算强非线性范围内微气压波峰值。另外，式(3)相对于式(2)具有明显的改善效果及工程应用价值。

6 结 论

借鉴国内外已有微气压波计算模型，在此基础上提出具有工程应用价值的参数化微气压波计算模型。采用高阶谱差分技术数值模拟微气压波传播过程，获取微气压波参数化计算公式。得出以下结论：

1)在速度为200 km·h-1、250 km·h-1、300 km·h-1、350 km·h-1时，微气压波声压峰值分别与隧道轴向距离r-0.87、r-0.86、r-0.85、r-0.83成正比。将实验数据与预测数据展开对比，吻合良好，证明该方法可行有效。

2)随着高速列车进入隧道的速度逐渐增大，式(3)中的参数α逐渐偏离1，进一步表明微气压波非线性特性随着高速列车穿越隧道的速度增大而逐渐增强。