基于模型预测控制的飞机蒙皮铣削方法研究
2022-08-15罗怡沁严伟鑫
罗 震,罗怡沁,严伟鑫
(1.江西洪都商用飞机股份有限公司,江西 南昌 330024;2.杭州钱江机器人有限公司,浙江 杭州 311231;3.浙江纺织服装职业技术学院机电与轨道交通学院,浙江 宁波 315211)
0 引言
工业机器人在加工、码垛及喷涂领域应用广泛,在金属切削制造领域更为突出[1]。随着机器人技术的飞速发展,基于复杂曲面加工理论研制机器人智能铣削装配系统,已成为满足市场化需求的关键[2-3],并能在航天、医疗和制造等领域实现应用与产业化。
金属加工常用的2种方式为专用数控机床与人工切削。相较于专用数控机床与人工切削的金属加工方式,机器人智能铣削具有成本低、空间可达性好和承载能力强等优点[4],但存在定位精度低、振动范围大等问题。为解决这类问题,通常采用比例积分微分(proportional integral differential,PID)[5]、滑模[6]、线性二次型调节器(linear quadratic regulator,LQR)[7]等控制方法。PID算法鲁棒性差,需要调节相应的参数才能得到较优的效果。滑模控制是1种变结构模式,存在抖振问题。LQR方法基于线性模型优化无限时域目标,难以处理控制量约束条件,不利于实际加工。模型预测控制(model predictive control,MPC)具有在不确定性环境下进行约束优化控制的共性机理,已在工业过程控制领域成功应用并取得巨大的经济收益[8]。然而,MPC算法的目标函数仅含误差和输入项,通过融入铣削力与进给量到目标函数,可得到效率与精度综合较优的结果。
本文根据C919型飞机机身蒙皮端面修切需要,建立铣削力数学模型,将周向铣削力与速度比值融入预测目标函数,优化得到机械臂关节输出;将输出导入铣削加工程序,完成蒙皮自动化修切工艺。该研究为自动化铣削加工提供借鉴。
1 机械结构分析
C919机身桶段蒙皮端面修切系统由五大部分构成,主要包括飞机蒙皮、支座、固定架、激光跟踪仪和自动修切设备。C919机身桶段蒙皮端面自动修切整体如图1所示。其中,自动修切设备包括KUKA机器人、末端执行器、自动导引运输车(automated guided vehicle,AGV)移动平台、外部轴升降系统、液压系统、基座等。其工作流程为:液压系统通过伸缩机构提高自动修切设备的整体高度,将修切设备置于AGV移动平台上并随平台运动到待加工位置;同时,外部轴的升降功能可调整机械臂的基座位置,实现飞机机身蒙皮不同高度位置的切削。
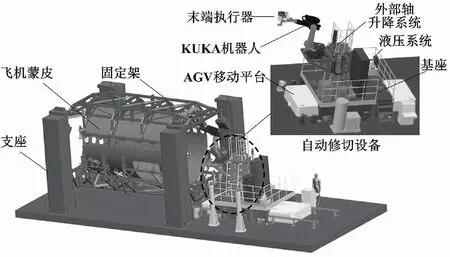
图1 C919机身桶段蒙皮端面自动修切整体图
铣削机器人选用负载能力强、工作稳定性好、关节臂长的KR 210 R2700关节型KUKA六轴机器人,负载率为31.3%。该型号机器人在完成铣削工作时,能承受变化的铣削力冲击,铣削加工空间能达到较大范围要求。机器人运动空间如图2所示。
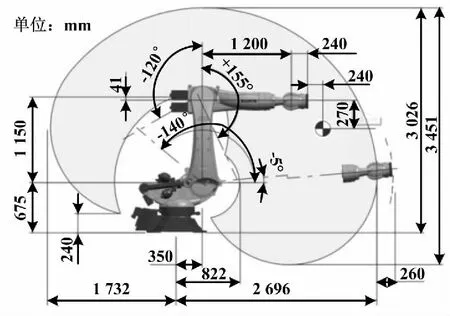
图2 六轴机器人运动空间图
1.1 坐标系转换
在机身桶段蒙皮端面自动修切系统中,需定义正确的坐标系关系,从而保障机器人定位准确、铣削顺畅。对此,本文建立并给出机器人切铣系统的各坐标系,完成机器人的路径规划。机身桶段蒙皮端面自动修切系统主要包括装配、工件、激光跟踪仪、机器人移动平台、机器人基座、机器人法兰和刀具等坐标系。系统通过建立各坐标系的转换关系,确定各坐标系的位置关系,以确保机器人找到准确的位置,实现蒙皮端面加工。图3为两坐标系间的复合变换图。

图3 两坐标系间的复合变换图
2种变换存在于坐标系{A}与{B}之间,分别为坐标平移和旋转。在坐标系{A}中,p点的位置为:
Ap=ARBBp+ApBo
(1)
式中:Ap为p点在坐标系{A}中的位置坐标;ARB为坐标系{B}到坐标系{A}的旋转矩阵;ApBo为坐标系{B}原点在{A}的位置坐标。
将位置和姿态变换组合为齐次矩阵,则式(1)可改写为:
(2)
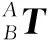
结合坐标系变换原则,本系统采用Denavit-Hartemburg(DH)法构建KUKA机器人运动学模型。构建过程为:首先,对每个杆件进行编号,由数字0~6依次给底座末端法兰直至连杆编号完毕;其次,定义随旋转关节旋转的z轴轴线方向;再次,定义xn关节坐标系的方向为两轴zn-1与zn之间相距最小的共线垂线方向;最后,建立y轴各关节方向遵循右手原则。根据上述原则,绘制的KR 210 R2700型KUKA六轴机器人坐标系如图4所示。
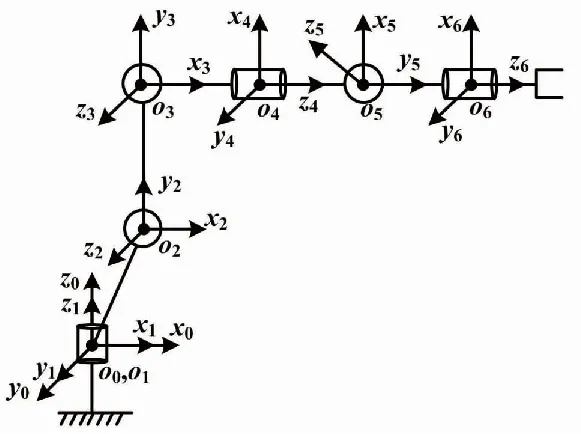
图4 六轴机器人坐标系
分析机器人的运动学模型,根据相邻关节坐标系的位姿关系,给出了如表1所示的KR 210 R2700型KUKA六轴机器人的DH参数。位姿关系用θ、α、a、d这4个参数表示。
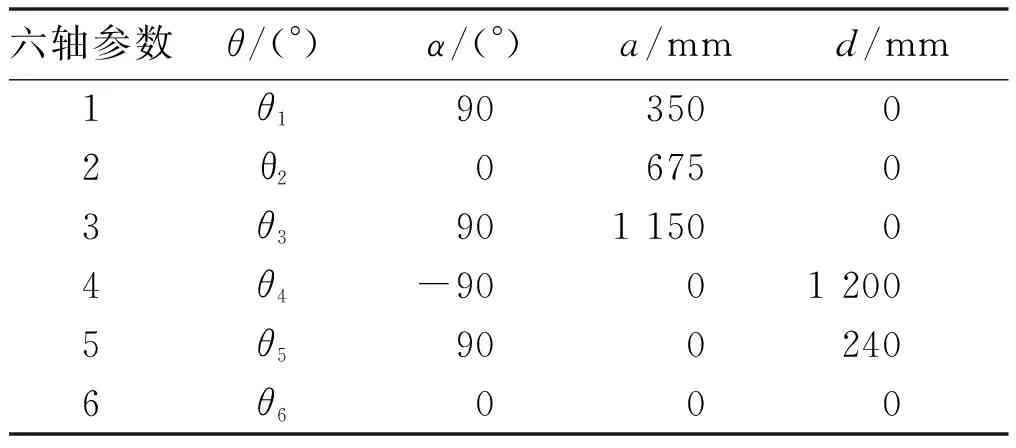
表1 KR 210 R2700型KUKA六轴机器人DH参数表
1.2 位置反解
由DH法建立相邻关节间的齐次转换矩阵可表示为:
(3)
式中:i为第i个关节;cθi=cosθi;sθi=sinθi。
机械臂正解可由相邻转换矩阵连乘得到,则机械臂末端与基座映射关系为:
(4)
式中:R为末端姿态矩阵;P为末端三维位置。
六轴机械臂运动学反解,就是在获取机械臂姿态与末端位置的前提下,求解各驱动关节的转角值。一般而言,机械臂后3个关节z轴相交于1点,可利用代数法进行求解。
结合机械臂的结构特点,采用位姿分离法,根据机械臂位置求解关节1~关节3的转角,再基于姿态分析关节4~关节6的转角解析表达式。
(5)
根据式(5)等式两端相等,可得:
(6)
式(5)左端可简写为:
(7)
(8)
借助式(8)得到关节2和关节3的转角θ2和θ3。
(9)

值得注意的是,转角θ2和θ3均存在2组解,两者存在绝对值之和等于π的代数关系,只需要取绝对值较小的即可。
在已知转角θ1、θ2和θ3时,对于关节4~关节6的转角,可利用式(8)中等式两端姿态矩阵相等得到[9]。
(10)
式中:θ23=θ2+θ3。
2 切削路径规划
依照飞机蒙皮端面切削任务,首先规定预期的机械臂末端运动轨迹,再将路径点离散化,从而追踪点位信息,即得到机器人的加工轨迹规划。
2.1 切削路径规划预期
蒙皮端面的切削路径规划要完成以下预期。①设置中间过渡点,引导机器人随着预期的切削路径动作;在此运动中,应减少铣削刀具与蒙皮端面产生撞击。②改善铣削不间断动作的振动性,提高机器人末端刀具的定向概率,以保证飞机蒙皮端面的铣削质量,并得到较高的轨迹切削精度。③预先规划铣削刀具动作中的位姿,设计最优轨迹曲线,增强铣削加工连续工作的强度,以提高运动稳定性。
2.2 加工路径规划方案
2.2.1 流程规划
飞机机身蒙皮端面切削的路径流程设计是一项重要内容。首先,通过激光跟踪仪获取端面的外型尺寸数据;然后,根据机器人末端刀具在目标加工点的修切位姿需要,采用坐标变换法规划切削末端与端面相交处的位置和姿态轨迹。
目标切削端面是不规则的空间自由曲面,加工过程中刀具需要进行不间断的平滑动作。
具体实现流程如下。首先,将飞机蒙皮端面的SolidWorks模型转成STP格式并导入RobotMaster以获取蒙皮轮廓,再将该轮廓空间轨迹平移一定距离。该距离为蒙皮切削半径。平移后得到的新轨迹就是刀具切削路径。接着,固定蒙皮端面模型和机器人基座标的相对位置,从而确保机器人加工方向与蒙皮端面法向矢量一致。刀具随路径点位连续动作的路径越来越与预期的加工轨迹相近。然后,在RobotMaster软件中选取指定的蒙皮轮廓,利用中值功能自动生成机器人程序。最后,通过运行程序增强刀具的切削强度,降低切削振动。
2.2.2 路径规划
在测试阶段,飞机蒙皮端面模型放置位置与理论位置有偏差。此时,使用CAD点的yz坐标生成机器人加工路径。首先,在SolidWorks中导出蒙皮端面模型,再导入CAD中,利用测量的飞机蒙皮端面实际点yz坐标求出刀具的法向角度;然后,用yz坐标和法向角度生成KUKA机器人执行程序SRC和DaT。试验时,测试蒙皮的左下与右下部。
在CAD中去除飞机蒙皮轨迹中心点作40条法线阵列线,将蒙皮轨迹打散为40个离散点。以阵列点作为机器人加工程序点、阵列的法线角度作为刀具的法线角度,供扫描与加工程序时使用。
由于高阶样条曲线具备局部支撑性,且改变一个控制点不会影响整个拟合函数,确保了曲线更接近所有控制点[10]。在提取40个离散点的基础上,利用B样条曲线拟合离散点,能够保证加工轨迹的连续性与精确性。n阶B样条曲线可表示为:
(11)
式中:k为B样条曲线的阶数;dj为B样条控制点;ui为归一化节点向量变量,可以用累积弦长法得到;Nj,k(ui+k)为B样条的基函数。
(12)
为求解(m+k-1)个控制点,式(11)给出了m个方程。额外的(k-1)个方程可以由初始和最终点处的边界条件创建。边界条件包括在2个末端时刻对速度和加速度的运动学约束。边界条件取B样条在两端点处的r阶导数pr(u)。r阶导数可表示为:
(13)
速度和加速度的运动学约束的边界条件为:
(14)
式中:V(t0)、V(tm)、A(t0)和A(tm)分别为机器人驱动器在初始和最终位置的角速度和加速度,可以通过递归公式(12)计算。
3 轨迹跟踪控制算法
3.1 铣削力目标函数
对于典型的螺旋角为β的立铣刀,铣削力是通过将每个离散切削刃部件对应的各个力分量相加所得的。假设轴向切割深度为常数。铣刀片的几何模型如图5所示。
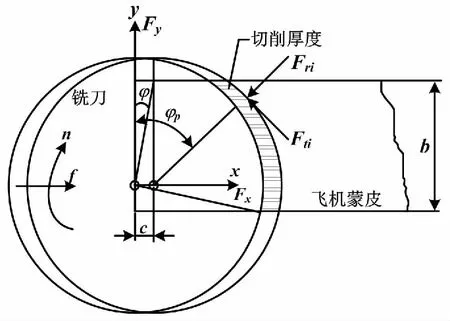
图5 铣刀片的几何模型
3.2 建立预测模型
以铣刀的1个切削齿尖为基准,假设其角度为φ、齿角节距为φp,则其余齿的齿尖按以下给出的角度定位为:
φj(0)=φ+jφp,j=0,1,...,N-1
(15)

φj(z)=φ+jφp-kβz
(16)
作用在长度为dz的切削刃基本部分上的铣削力的切向分量、径向分量和轴向分量表示为:
(17)
式中:hj(φ,z)为铣削厚度,hj(φ,z)=csinφj(z);c为进刀量;Ktc、Krc和Kac分别为切向、径向和轴向的铣削力系数。
根据文献[11]可知,蒙皮铣削表面粗糙度Ra与周向铣削力Ft近似为线性变化关系。表面粗糙度直接影响铣削精度,即周向铣削力与铣削精度成正相关。由式(19)可知,当设定刀具自转转速、公转转速、每齿进给量和铣削深度为常量时,周向铣削力与进给量c成正比。另一方面,每分钟进给量与机器人铣削效率成反比。因此,将刀具的进给量与机器人末端速度的比值设置为模型预测的目标函数之一,以实现铣削精度与效率的合理权衡。
根据机械臂的位置反解建立系统的状态空间方程,并对其进行离散化处理。
X(tk+1)=AsX(tk)+BsΔuk
(18)
Y(tk)=CsX(tk)
(19)
式中:X(tk+1)为铣刀与飞机蒙皮接触位置,X(tk+1)=[xyz]T;Δuk为机械臂末端的位置输入量,Δuk=[ΔxΔyΔz]T;As、Bs和Cs为单位矩阵。
采用基于有限时域最优控制问题的求解的模型预测控制,在任何采样时间tk,最小化成本函数的控制序列u[tk,tk+N-1|tk]:=[u0(tk),u1(tk),…,un-1(tk)]。其中,N≥1为预测时域。最小化的成本函数可表示为二次函数:

为了解决动态面板模型的内生性问题,本文采用系统GMM估计方法。面板数据GMM估计方法主要由差分估计法和系统GMM估计法构成,二者的不同之处在于差分估计法易导致弱工具变量问题的出现,而系统GMM估计法不仅可以弥补差分估计法的缺点,还可以增加工具变量的个数以解决模型的内生性问题。鉴于文章选取样本有限,以及考虑到异方差和序列相关问题,决定采用两步系统GMM估计法[17]。
(20)
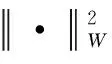
成本函数(22)受制于由系统(20)的动态所表示的硬约束,以及对状态和输入变量的不等式约束,即:
Xi(tk+N)∈x
(21)
式中,j=1,2,…,N-1。
xf为终端集,需满足式(22)所示的约束条件:
(22)
kif[ei(tk)]=KLQei(tk)
(23)
式中:KLQ为具有相同代价函数的无限时域线性二次型控制器的控制增益。

δi(tk)∈xf
(24)


(25)
矩阵Pi可采用黎卡提方程进行求解。
(26)
根据滚动时域策略,适用的分段恒定控制律为:
ui(t)=kMPC[ei(tk)],t∈[tk,tk+1)
(27)
式中:T为MPC的采样时间,T=tk+1-tk。
(28)
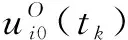
鉴于不确定性扰动和模型不准确等因素的影响,基于控制系统的状态量预测机械臂末端下一周期的位置输出,返回校正。在优化得到新的位置控制序列后,滚动优化控制输出以实现系统的轨迹跟踪。
基于模型预测的轨迹跟踪控制流程如图6所示。
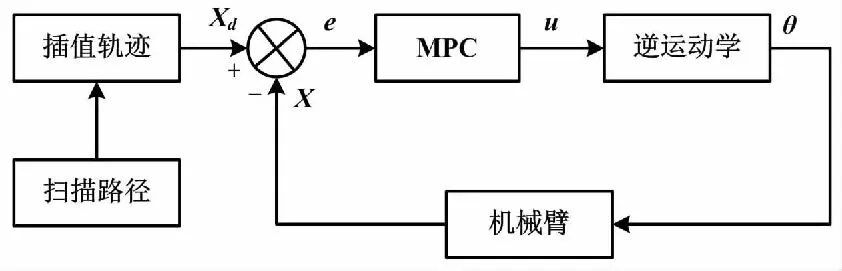
图6 基于模型预测的轨迹跟踪控制流程
4 蒙皮端面铣削试验与分析
4.1 激光跟踪仪安装
激光跟踪仪通过跟踪并测量机器人坐标系获取点位信息,计算机器人坐标系与飞机坐标系点位数据转换的差值。原点建立在激光跟踪仪检测头的中心。
在精度优化之前,需要将激光跟踪仪与蒙皮端面自动修切系统连接。首先,将激光跟踪仪装到重型三脚架上,并移到固定位置,踩落重型三脚架;然后,检查末端执行器是否安装机械控制传感器(mechunical automatic control transducer,T-MAC);最后,将激光跟踪仪的激光连到T-MAC上,以检测激光跟踪仪和T-MAC是否正常工作。以上步骤完成后,则激光跟踪仪与蒙皮端面自动修切系统联接完毕。
4.2 蒙皮端面铣削试验
机身桶段蒙皮端面自动修切系统加工流程为先加工左侧后加工右侧。由于每侧均有上下两部分,所以加工顺序依次为左上、左下、右上、右下。以下为关键试验步骤。试验在自开发仿真软件中展开。首先,试验建立坐标系,并导入飞机坐标系。飞机坐标系是通过激光靶球测量地板网格8个点坐标,用海克斯康激光跟踪仪测量软件Spirial Analyze(SA)生成。然后,在系统中导入蒙皮端面数据。为保证机械臂铣削加工作业的稳定性,将铣削起点与终点处的速度与加速度参数设置为0。接着,系统根据导入的数据进行自动计算。所需计算的数据分别为每刀加工量(最后一刀为精加工,其余为粗加工)、加工线速度、加工电主轴转速、加工目标值(x轴方向)和加工余量。最后,在标定界面中建立机器人坐标系;自动运行界面中的10个点,记录机器人、激光跟踪仪坐标,采用最佳拟合法计算准确的机器人坐标系;记录理论点(飞机坐标系)与实际点坐标的数据。
在蒙皮端面左上、左下、右上、右下四部分铣削时随机选取10个点,按照每次修切1 mm的规则,对比优化前铣削结果。蒙皮端面铣削优化前后对比如图7所示。图7中显示了修切精度的变化。
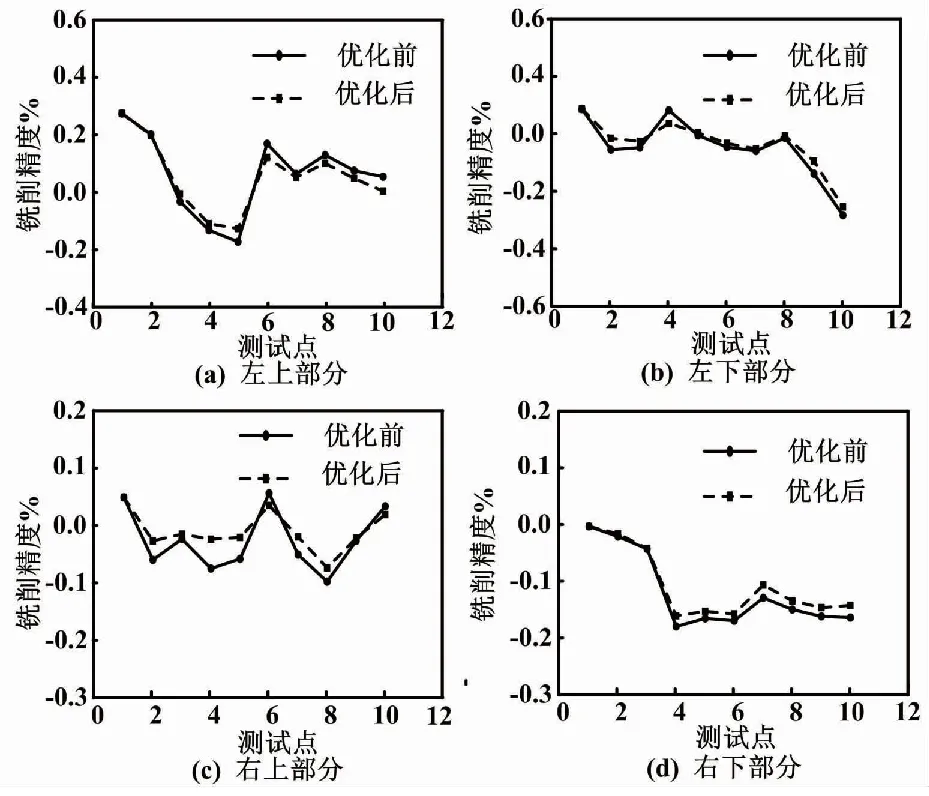
图7 蒙皮端面铣削优化前后对比折线图
由图7可知,各部分10个测试点修切后的精度中:左上有1个在0.2 mm左右,左下有1个在0.2 mm左右,右下有7个在0.2和0.1 mm左右,其余都小于等于0.1 mm。该结果能够较好地满足通用技术指标AS 9100的技术规定:修切系统重复定位精度≤±0.1 mm,修切系统绝对定位精度≤±0.3 mm,且每次修切后的精度波动值较小。同时,优化后的铣削精度均较好,验证了所提算法的有效性。需要说明的是,优化前是仅根据激光跟踪仪的测量反复铣削,以达到相应的铣削量。修切精度的变化原因在于机械加工造成蒙皮断面各位置的材料属性不同。在飞机蒙皮各位置进行重复试验。多组试验结果能够很好地验证离散化自动修切轨迹的合理性。
5 结论
本文针对利用机械臂铣削精度低的问题,提出一种基于模型预测控制的离散化轨迹自动铣削方法。该方法采用DH法推导运动模型,利用激光跟踪仪标定飞机蒙皮和机器人坐标系,将蒙皮断面轮廓离散化为加工路径,并利用B样条曲线拟合。本文建立了包含铣削周向力与进给速度比值的预测目标函数,并通过多组重复试验验证了铣削方法的可行性和合理性。
研究结果表明,通过扫描飞机蒙皮轮廓,利用B样条曲线拟合得到铣削轨迹,实现修切重复定位精度和修切绝对定位精度分别在±0.1 mm和±0.3 mm以内。该结果验证了所规划轨迹的连续性和平滑性。此外,该研究引入铣削周向力与进给速度比值到预测的目标函数,综合考虑了铣削效率与精度,优化后精度得到一定幅度的提高。该结果验证了控制算法的有效性。
