色玻璃凝聚理论中跑动耦合常数效应研究

向文昌， 王梦亮*， 蔡燕兵， 周代翠

(1.贵州财经大学金融物理重点实验室， 贵阳 550025； 2.华中师范大学粒子物理研究所， 武汉 430079)

色玻璃凝聚(Color Glass Condensate，CGC)有效理论通常被认为是描述高温高密QCD环境中强相互作用的最佳理论之一.领头阶(Leading Order，LO)CGC理论最早起源于20世纪90年代后期，主要是推导了描述胶子饱和物质非线性演化的Balitsky-JIMWLK方程[1-5].Balitsky-JIMWLK方程是一个无穷级联方程，无法直接用于唯象研究.在平均场近似下，Balitsky-JIMWLK方程将简化为一个闭合的演化方程，即Balitsky-Kovchegov(BK)方程[1，6].BK方程只对所有领头对数项～αsln(1/xBj)进行重求和，因此属于LO方程，其精度不高，这里αs和xBj分别表示跑动耦合常数和Bjorken变量.该方程能直接用于唯象研究，如描述HERA能区质子结构函数[7]、RHIC能区氘-金碰撞中带电粒子的横动量分布[8]、LHC能区质子-铅碰撞和铅-铅碰撞中末态粒子的多重数分布[9]等.然而，大量的研究表明LO CGC理论只能定性的描述实验数据，究其原因发现LO BK方程给出的偶极子散射振幅随快度的演化速度过快，导致理论计算结果普遍大于实验数据.

近十几年来，大量的研究致力于推广LO CGC理论到次领头阶水平.一方面是由于LO CGC机制描述的实验观测量也能采用DGLAP演化机制描述，如HERA能区电子-质子深度非弹性散射(DIS)中几何标度效应[10-11].高能核物理学家们还无法甄别到底是CGC机制还是DGLAP机制主导高能强子碰撞初期形成的部分子系统的演化，因此CGC有效场理论还没有被高能核物理学家广泛接受.另一方面是由于LO CGC理论精度水平还有待提高，低精度的LO CGC还无法对DIS中单举约化截面以及相对论重离子碰撞中带电粒子多重数分布给出定量的描述，通常需要乘上一个常数因子才能解释相关实验数据.以上两点主要原因极大的推动了CGC理论向次领头阶(Next-to-Leading Order，NLO)发展.

在NLO-CGC理论发展方面，最初由Balitsky研究组[12]和Kovchegov-Weigert研究组[13]采用不同的重整化方案考虑夸克圈对胶子传播子的修正贡献，对所有阶αsNf进行重求和，分别推导并获得了两种版本的跑动耦合常数效应修正的Balitsky-Kovchegov演化方程(rcBK).值得注意的是这两个rcBK方程具有相同的形式，但是演化核不同.rcBK方程的数值解显示其给出的偶极子散射振幅随快度的演化远小于LOBK方程给出的结果，由此表明次领头阶的跑动耦合常数效应极大的压低了CGC物质的演化速度.当Albacete等人把rcBK方程用于描述HERA实验数据时发现，在一定的误差范围内rcBK方程能较好的给出定量的描述，而且不再需要乘上一个常数因子[14].此外，研究组在饱和区域解析地求解了rcBK方程，研究发现在饱和区域中Balitsky演化核和Kovchegov-Weigert演化核具有相同的表达形式，由此表明CGC演化方程在饱和区域中独立于重整化方案[15].同时，还获得了偶极子散射振幅的解析表达式，并发现散射振幅对快度的依赖从LO下的平方依赖变成了跑动耦合常数下的线性依赖，表明了跑动耦合常数效应对CGC物质演化有较强的压低作用[16].

除夸克圈修正(跑动耦合常数效应)外，胶子圈的贡献也是一种非常重要的NLO修正.在考虑了夸克和胶子圈的贡献后，Balitsky和Chirilli推导了一个完整的NLO BK演化方程[17].胶子圈修正不仅修改了方程的演化核，而且还改变了演化方程的形式(相较于LO BK方程)，因此使得NLO BK方程极其复杂.在BK形式表示的NLO演化方程发展的同时，Kovner等推导了NLO JIMWLK哈密顿量，并采用该哈密顿量重新推导出了NLO NK方程[18-20].NLO BK方程出现八年后，Lappi研究组才首次利用数值方法解出了该方程，并获得了NLO偶极子散射振幅[21].但是其研究发现NLO BK方程给出的散射振幅对初始条件有很强的依赖关系，同时散射振幅会随碰撞能量的增加而变成负值.这些非物理的结果表明NLO BK方程极其不稳定，究其原因主要来自于演化核中大双对数项的贡献.为了解决以上提到的不稳定性问题，Iancu研究组考虑到连续部分子辐射过程中，辐射胶子寿命需满足时序限制性条件，对大双对数项进行重求和[22].同时，也考虑了单对数项重求和的贡献，得到了一个共线改进的Balitsky-Kovchegov演化方程(ciBK方程).ciBK方程成功地解决了NLO BK方程不稳定的问题.Albacete课题组和Iancu研究组在3种不同的跑动耦合常数方案下，分别采用了ciBK方程研究了HERA实验数据，研究结果显示ciBK方程给出了更好的理论描述[23-24](相较于LO-BK和rcBK方程).最近，Beuf等考虑到NLO影响因子对光子波函数的修正作用，采用3种不同的偶极子散射振幅，研究了DIS约化截面，结果显示3种散射振幅给出了同等质量的描述效果[25].仔细分析以上3个课题组的研究结果不难发现，他们在拟合实验数据时都把一圈QCD表示的跑动耦合常数表达式中的常数因子exp(-γE)当作自由拟合参数C，其中γE～0.6.然而拟合结果显示为了使偶极子散射振幅的演化速度与实验数据的要求相一致，C的取值跨越了非常大的范围(0.31～8050).由此可知偶极子散射振幅对跑动耦合常数效应较为敏感，也反应出跑动耦合常数效应的重要性.

本论文将基于LOBK方程和ciBK方程，结合HERA能区电子-质子DIS约化截面相关实验数据，着重研究4种不同的跑动耦合常数方案对偶极子散射振幅的影响，即母偶极子大小、最小偶极子尺度、快速收敛和Balitsky 4种方案.在将C限定在其理论值附近变化和让C完全自由变化两个情况下研究跑动耦合常数对偶极子散射振幅的影响，发现让C完全自由变化时所有跑动耦合常数方案给出了几乎同等的实验数据描述效果(χ2/d.o.f～1.15).然而，当限定C的变化范围在其理论值附近时，母偶极子大小和最小偶极子尺度方案无法对实验数据给出合理的描述，究其原因是此时散射振幅随快度的演化速度过快，而跑动耦合常数效应又没有提供足够多的压低量来抵消过快的演化速度，从而导致理论计算结果大于实验观测值.在限定C的变化范围下，快速收敛和Balitsky方案给出了较好的实验数据描述效果，尤其是采用Balitsky方案拟合得到的C值与理论计算值非常接近，由此也间接表明了Balitsky方案可能是一种优选方案.值得注意的是在极限运动学条件下Balitsky方案将简化为最小偶极子方案，即Balitsky方案包含了部分最小偶极子方案的内容.

1 偶极子演化方程

为了引入一些基本物理量的记号，本节将首先介绍偶极子随快度演化(或能量演化)的领头阶Balitsky-Kovchegov方程；然后回顾共线改进的Balitsky-Kovchegov方程.这两个方程将在后面的研究中用于描述HERA能区相关实验数据.

1.1 领头阶Balitsky-Kovchegov方程

在高能情况下，考虑一个由夸克—反夸克对组成的偶极子与强子靶发生散射(图1).假定该散射过程满足程函近似，即意味着夸克的横向坐标(x)和纵向坐标(y)在散射过程中保持不变，该过程的散射矩阵可以用两条Wilson线的关联函数表示：

图1 偶极子与靶发生相互作用的费曼图

(1)

这里，〈…〉Y表示在快度Y一定时对靶胶子场的平均，Y为偶极子与靶之间的相对快度：

(2)

式中，s和Q0分别为质心系能量的平方和靶的典型饱和动量.方程(1)中的U为时序Wilson线，可以表示为：

(3)

式中，A+(x-，x)为靶中的胶子场.

在平均场近似下，散射矩阵Sxy(Y)随快度的演化满足BK方程[1，6]：

[Sxz(Y)Szy(Y)-Sxy(Y)]，

(4)

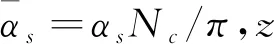
在大Nc极限下，方程(4)描述了母偶极子(x，y)随着快度的增加劈裂成两个子偶极子(x，z)和(z，y)的过程，演化核KLO(x，y，z)表示劈裂的几率：

(5)

通常把方程(4)右边的第一项叫做“实”项，它描述两个子偶极子同时与靶发生相互作用，因此它也是非线性项.方程(4)右边的第二项通常称为“虚”项，它描述母偶极子在相互作用过程中没有被分解而是存活下来的概率.值得注意的是，在方程(4)只对领头对数进行了重求和，并假定了跑动耦合常数不变，因此方程(4)属于领头演化方程.

利用散射矩阵和散射振幅之间的关系：

S=1-N，

(6)

把LO BK方程可以改写成散射振幅表示：

N(r2，Y)-N(r，Y)-N(r1，Y)N(r2，Y)].

(7)

式中，r=x-y，r1=x-z，r2=z-y分别代表母偶极子和两个子偶极子横向尺度大小.方程(7)将便于对其求数值解.

1.2 共线改进的Balitsky-Kovchegov方程

当同时考虑到夸克圈和胶子圈的贡献时，可以得到一个描述偶极子随快度演化的完整NLO BK方程[17]：

[S(r1，Y)S(r2，Y)-S(r，Y)]+

[S(r1，Y)S(r3，Y)S(r′2，Y)-S(r1，Y)S(r2，Y)]+

[S(r′1，Y)S(r2，Y)-S(r1，Y)S(r2，Y)]，

(8)

其演化核：

(9)

(10)

(11)

这里采用了记号r′1=x-z′，r′2=y-z′和r3=z-z′.方程(9)中的b和μ分别代表β函数的系数和重整化标度.由引言部分的介绍可知，NLO BK方程的解对初始条件具有很强的依赖性，同时该方程的解会随着快度的增加出现负值，这些非物理意义的结果表明NLO BK方程不稳定，究其原因发现方程的不稳定性来自于NLO BK方程的演化核中大双对数项的影响，即方程(9)中的最后一项.为了使NLO BK方程稳定，Iancu等人采用了一种新颖的方法对所有大双对数项和单对数项进行重求和，得到了一个共线改进的演化方程(ciBK)[22，24]：

[S(r1，Y)S(r2，Y)-S(r，Y)]，

(12)

其中，共线改进的演化核：

Kci(r，r1，r2)=KSTL×KDLA，

(13)

单横向对数演化核KSTL为：

(14)

双对数近似演化核KDLA为：

(15)

2 跑动耦合常数

根据胶子传播子的Schwinger-Dyson方程的研究以及格点QCD结果表明：在坐标空间中，在r很大的红外区间，跑动耦合常数将会趋向常数αfreeze(本文取0.7)[26]；而在r很小的紫外情况下，基于强相互作用“渐近自由”的属性，耦合常数趋于0.因此，采用一圈精度的跑动耦合常数表达式：

(16)

从NLO BK方程(8)的演化核(9)中可以看出跑动耦合常数可能会使单对数项变得很大，如当r≫1/μ或r≪1/μ时，第一个单对数项就会趋于很大的值.因此，高能核物理学家们需要恰当的选取μ来消除这些潜在的大对数结果.通常情况下μ的选取不是唯一的，在微扰QCD中一般采用硬标度来确定跑动耦合常数.本文将采用4种不同的方案来选取μ，尽可能使得潜在的大对数项被抵消掉.

1) 在最早的研究中，通常认为QCD跑动耦合常数是母偶极子横向尺度大小的函数[12]，通常称为母偶极子大小方案：

(17)

式中，rpd代表母偶极子横向大小，pd为parent dipole的缩写.后来的研究发现，虽然母偶极子大小方案避免了大对数项，但是该方案很难对HERA实验数据给出较好的描述.

2) Balitsky和Chirilli在推导NLO BK方程时发现跑动耦合常数应该是最小偶极子横向大小的函数而非母偶极子横向大小的函数[16-17]，通常称为最小偶极子尺度方案：

(18)

式中，rmin=min{r，r1，r2}代表最小偶极子的横向大小.在所有的运动学区域中，该方案都能成功得消除大对数项的贡献.

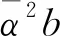
(19)

从方程(19)可知，当三个偶极子中的任意一个远远小于其他两个时，快速收敛方案将化简成最小偶极子尺度方案.

4)在唯象研究中，高能核物理学家们大多采用Balitsky推导rcBK方程的方案[24]，通常称为Balitsky方案：

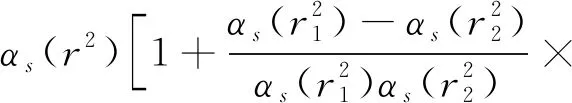
(20)

在极端运动学极限下，方程(20)也将化简为最小偶极子尺度方案.

3 数值结果

本节采用HERA能区电子-质子散射中约化截面的相关实验数据，研究不同跑动耦合常数方案的优缺点.根据Mueller偶极子模型，电子将辐射出虚光子，然后虚光子与质子发生深度非弹性散射，其截面可以表示为[27]：

(21)

(22)

(23)

(24)

采用约化截面(24)式拟合HERA实验数据.为了计算(24)式，首先需要计算(21)式中的偶极子散射振幅N(r，Y).

第一节中介绍的偶极子演化方程(7)和(12)，加上第二节中跑动耦合常数(16)，已经具备了求解偶极子散射振幅的所有基础.由于偶极子演化方程是极其复杂的积分微分方程，很难从中得到解析的偶极子散射振幅.本文将采用之前研究中开发的数值算法求解方程(7)和(12)，获取数值形式的偶极子散射振幅[28-30].本文采用GNU科学计算程序库(GSL)中的荣格库塔方法求解方程(7)和(12).把偶极子放在网格上，并把它平均分成512个离散点.同时假定偶极子散射振幅不依赖于碰撞参数，即N=N(|r|，Y).在数值解方程过程中有部分点没有落在网格上，将采用样条插值的方法计算它们的值.此外，采用带跑动耦合常数效应的McLerran-Venugopalan(rcMV)模型作为偶极子演化方程所需的初始条件[31]：

N(r，Y0)=

(25)

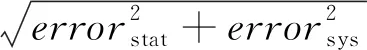
表1 ciBK情形下C2自由变化时拟合参数表

表2 ciBK情形下限定C2变化范围时拟合参数表

为了进一步解释在不限定C2的变化范围时，4种跑动耦合常数方案均给出了对实验数据合理的描述，而限定C2的变化范围时，上述4种方案中前两种无法合理的描述实验数据，后两种给出了合理的描述，采用表1和表2中的拟合参数画出了散射振幅随偶极子横向大小的变化关系，见图2.图2(b)显示了不限定C2变化范围的情形，从图可以看出在三个不同快度下(Y=0、6和12)，由4种跑动耦合常数方案计算得到的散射振幅分别相互聚集在一起，也即在同一快度时4种散射振幅近似相等.从表面上看，4种不同的跑动耦合常数方案应该导出不同大小的散射振幅.然而，对于同一快度得到它们的大小几乎相同.分析4种散射振幅近似相等的原因，发现主要来自于C2的贡献，通过改变C2的值能使4种不同的跑动耦合常数方案给出近似相等的耦合常数值.图2的左边给出了限定自由参数C2在其理论值周围变化的情况，从图可以看出对于同一快度散射振幅大致可以分成两组，一组是快速收敛和Balitsky方案给出近似相同大小的散射振幅，另一组是母偶极子大小和最小偶极子尺度方案给出近似相同大小的散射振幅，且前面一组小于后面一组，即前面一组对散射振幅的压低大于后一组，由此也解释了前面一组方案给出实验数据合理描述的原因.此外，研究发现在拟合中限定了C2的变化范围，从而无法通过调整C2的值来使得四种耦合常数的值近似相等，所以导致同一快度下散射振幅不相同，进而致使母偶极子大小和最小偶极子尺度方案无法对HERA实验数据给出较好的描述.

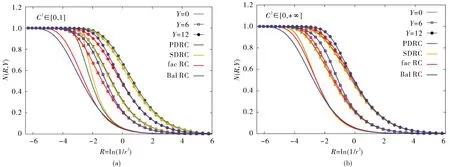
(a) 限定C2在理论值附近变化的结果；(b) C2自由变化的结果

图3中给出了不限定C2的变化范围时约化截面的理论计算值与HERA实验数据的比较情况.这里选取了九组不同的虚度值(Q2)对应的实验数据，从图中可以看出对所有的Q24种跑动耦合常数方案都给出了较好的描述.图4给出了限定C2的变化在其理论值周围的情况，从图中可以看出快速收敛(红色圆)和Balitsky(蓝色三角)方案能对实验数据进行较好的描述，而母偶极子大小(绿色方框)和最小偶极子尺度(黄色三角)方案在较大Q2时无法较好的描述实验数据.上述结果与表1和表2中的χ2/d.o.f完全一一对应.此外，考虑到C2的取值应接近其理论值，由表1、表2、图3和图4可知Balitsky方案可能是描述HERA实验数据的优选方案.

图3 不同虚度时四种跑动耦合常数方案下，约化截面随x的变化(在拟合时，没有限定自由参数C2的范围)

图4 不同虚度时四种跑动耦合常数方案下，约化截面随x变化(限定自由参数C2在其理论值附近变换C2～0-1)

为了验证LO情形下是否可以通过调节C2的值从达到压低偶极子散射振幅的目的，采用LO BK方程，结合4种不同的跑动耦合常数方案，拟合了同一组实验数据，相应的拟合参数见表3.从表3可以看出，无论C2取什么样的值，LO BK方程都无法对实验数据给出合理的描述.此外，由于母偶极子大小跑动耦合常数方案自身精度水平不高，加上LO BK方程也只考虑到了领头对数近似下的重求和贡献，因此采用LO BK方程拟合实验数据时无法得到合理的收敛结果.由此表明，只简单的把LO BK方程中的跑动耦合常数当作变量，而没有从pQCD原理出发通过计算NLO夸克圈(跑动耦合常数效应)的贡献，是不可能从实质上提高CGC理论的精度.

表3 LO BK情形下限定C2变化范围时拟合参数表

4 结论

本文首先回顾了LO BK方程和ciBK方程，然后介绍了四种跑动耦合常数方案，通过理论分析可知快速收敛和Balitsky方案在一定的极限下可以简化成最小偶极子尺度方案.由此说明快速收敛和Balitsky方案包含了部分最小偶极子方案的内容，这可能也是在拟合HERA实验数据过程的中发现快速收敛和Balitsky方案优于最小偶极子尺度方案的一个重要原因.此外，在偶极子模型框架下采用ciBK方程，并结合4种跑动耦合常数方案拟合了HERA能区光子-质子散射中约化截面，研究了4种跑动耦合常数方案的优越性.结果显示在不限定自由参数C2的取值范围时，4种方案对实验数据给出了相同质量的描述.分析其原因发现，对于同一快度通过调整C2的取值，可以使得4种跑动耦合常数方案对应的4个散射振幅具有近似相同的值.然而，当限定自由参数C2的取值范围在其理论值周围时，发现只有快速收敛和Balitsky方案能对实验数据进行合理的描述(其他两种方案计算出的约化截面偏离了实验测量值)，尤其是Balitsky方案不仅给出合理的χ2/d.o.f～1.15值，而且其给出C2～0.326的值也非常接近理论值0.3.由此可知Balitsky方案可能是描述HERA实验室数据优选的跑动耦合常数方案.为了显示跑动耦合常数效应对偶极子演化方程的重要影响作用，在LO BK方程中假定跑动耦合常数是一个变化量，从而简单且粗略的引入跑动耦合常数效应对偶极子散射振幅的修正.研究显示这种方法无法提高LO BK方程对实验数据的描述效果，可见简单的引入跑动耦合常数修正的方法无法从实质上提高偶极子散射振幅的精度.